Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Глава 9. Векторы
Содержание
- 1. Глава 9. Векторы
- 2. Понятие вектораМногие физические величины характеризуются числовым значением и направлением в пространстве, их называют векторными величинами
- 3. Понятие вектораОтрезок, для которого указано, какая его
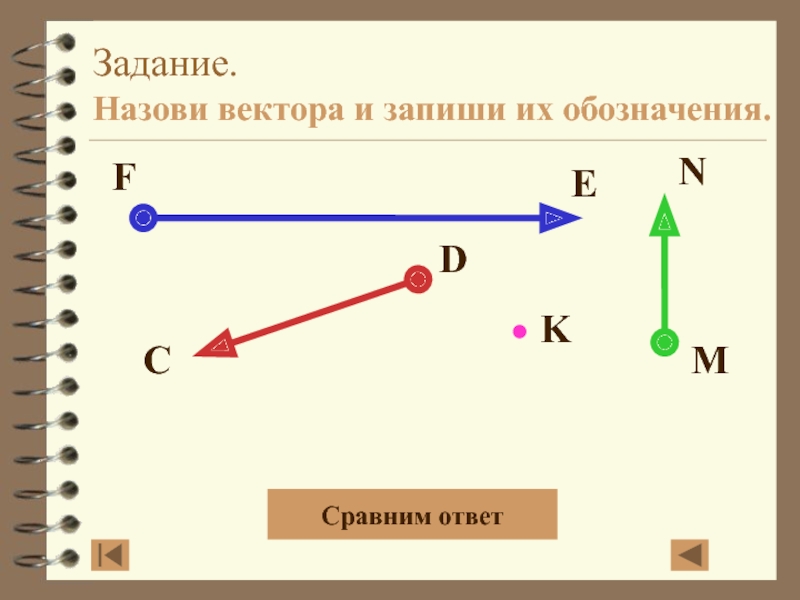
- 4. Задание. Назови вектора и запиши их обозначения.Сравним ответ
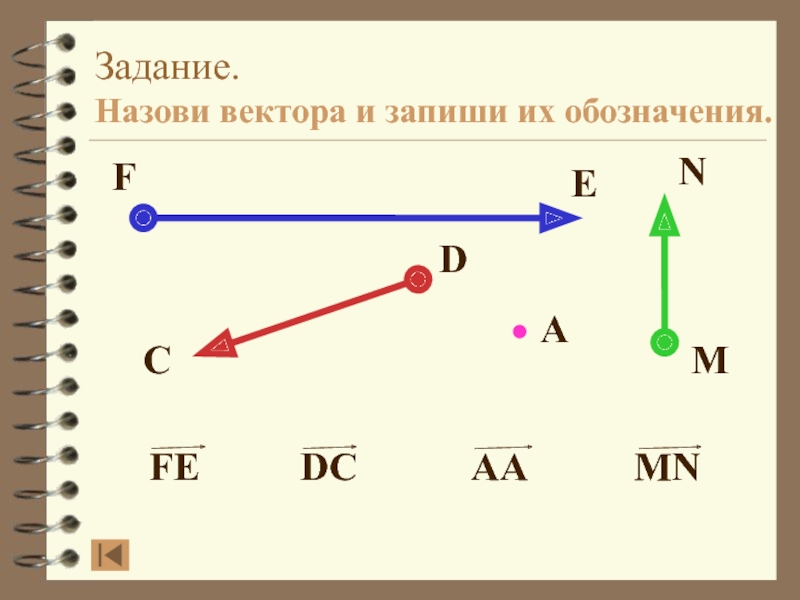
- 5. Задание. Назови вектора и запиши их обозначения.
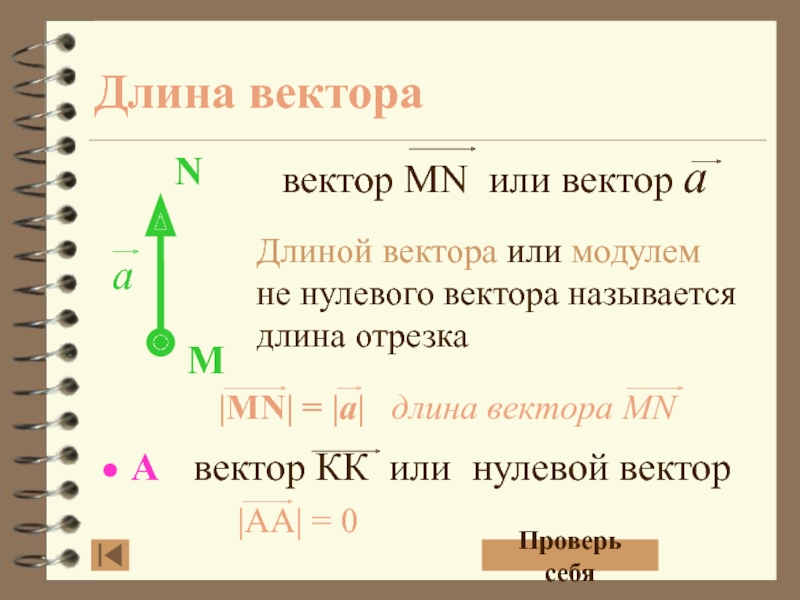
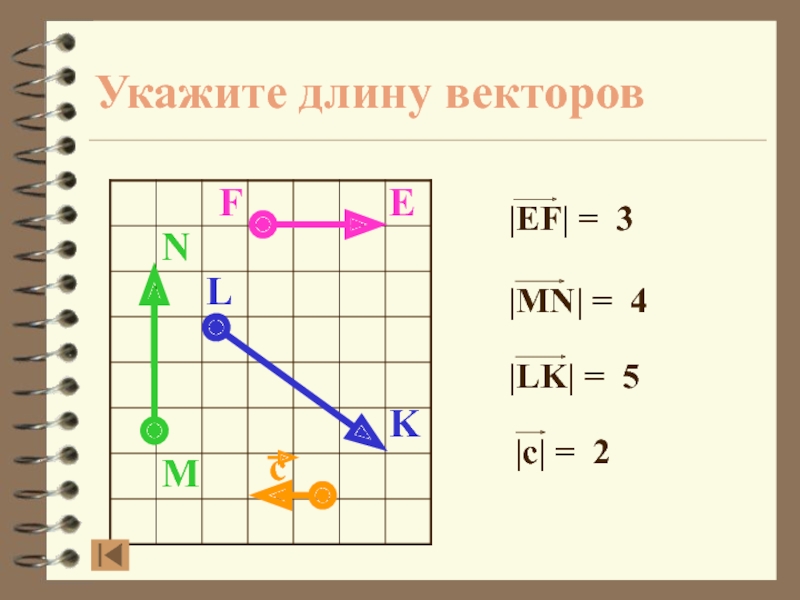
- 6. Длина вектораДлиной вектора или модулем не нулевого вектора называется длина отрезкаПроверь себя
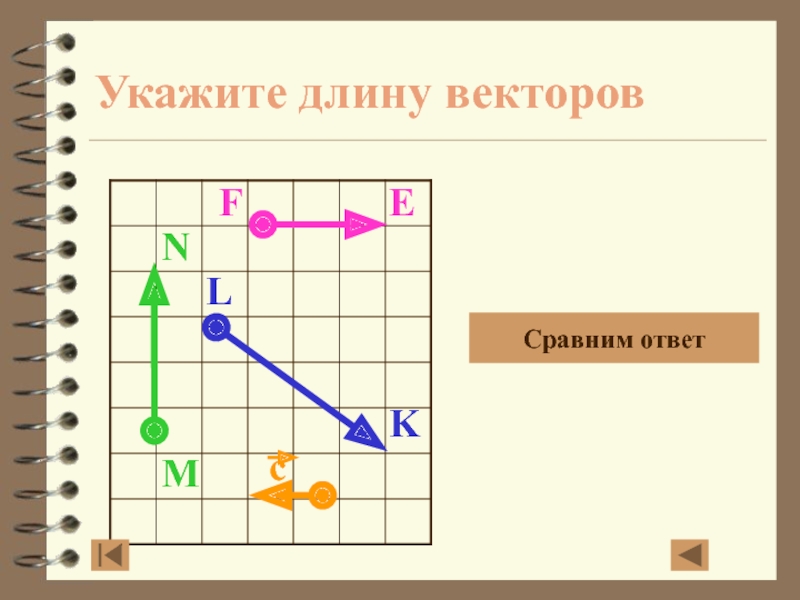
- 7. Укажите длину векторовMNFELKСравним ответ
- 8. Укажите длину векторов
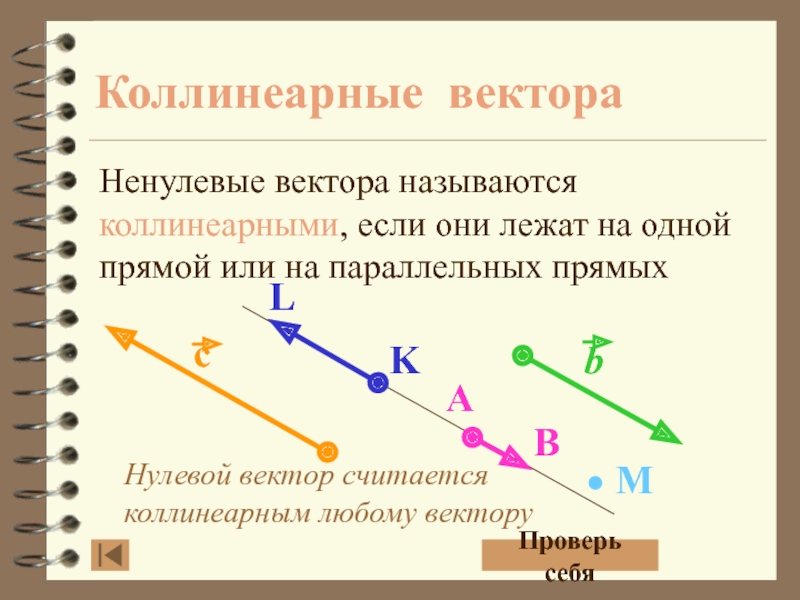
- 9. Нулевой вектор считается коллинеарным любому векторуКоллинеарные вектораНенулевые
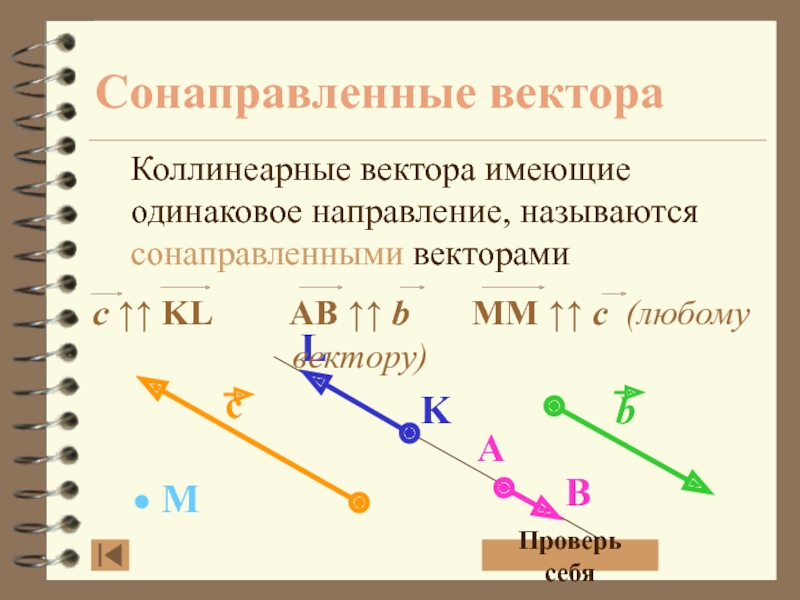
- 10. Сонаправленные вектораКоллинеарные вектора имеющие одинаковое направление, называются сонаправленными векторамиПроверь себя
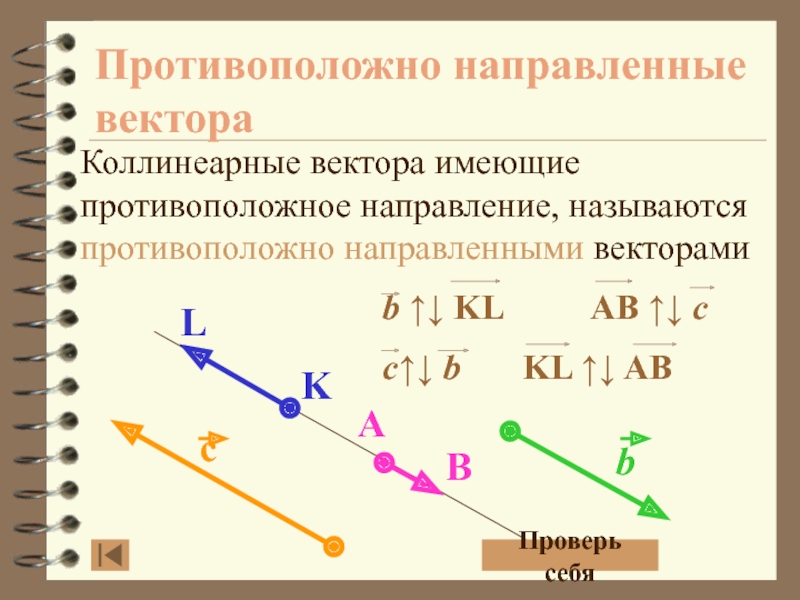
- 11. Противоположно направленные вектораКоллинеарные вектора имеющие противоположное направление, называются противоположно направленными векторамиПроверь себя
- 12. Типы векторов:
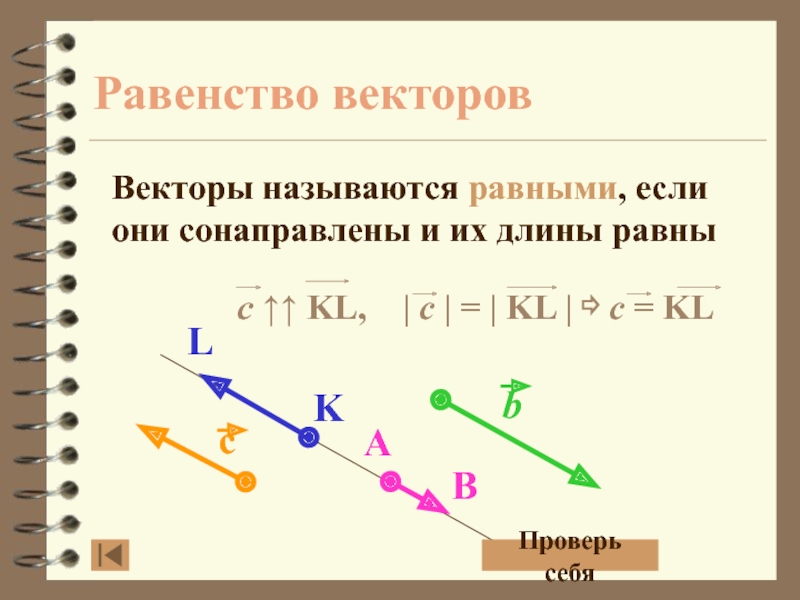
- 13. Равенство векторовВекторы называются равными, если они сонаправлены и их длины равныПроверь себя
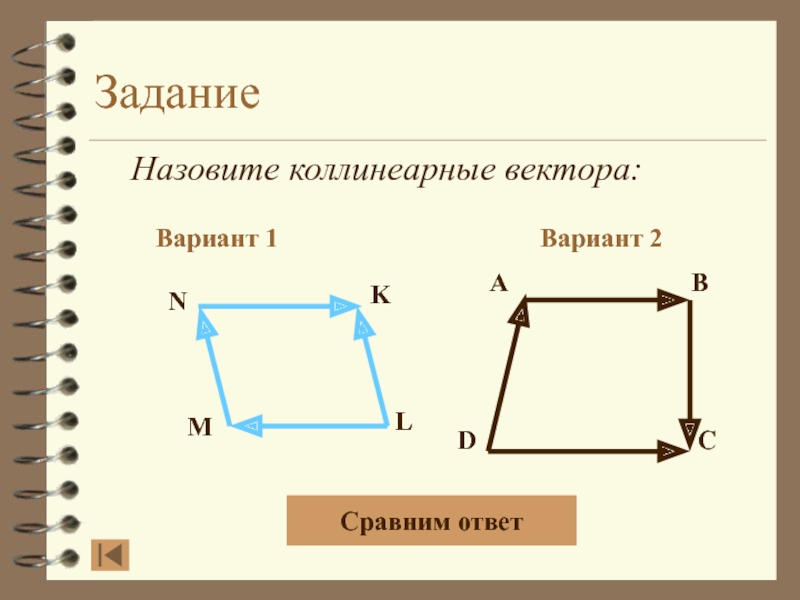
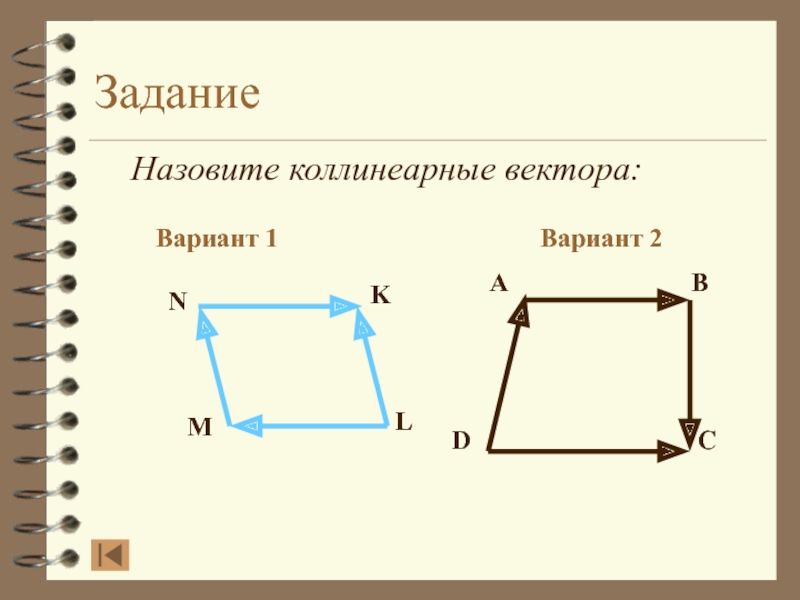
- 14. Задание Назовите коллинеарные вектора:Вариант 1Вариант 2ABDCNKLMСравним ответ
- 15. Задание Назовите коллинеарные вектора:Вариант 1Вариант 2ABDCNKLM
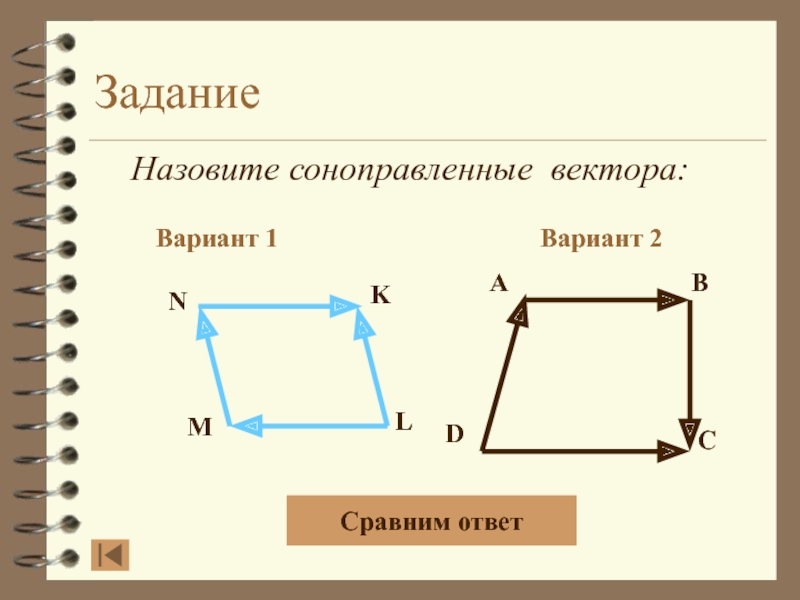
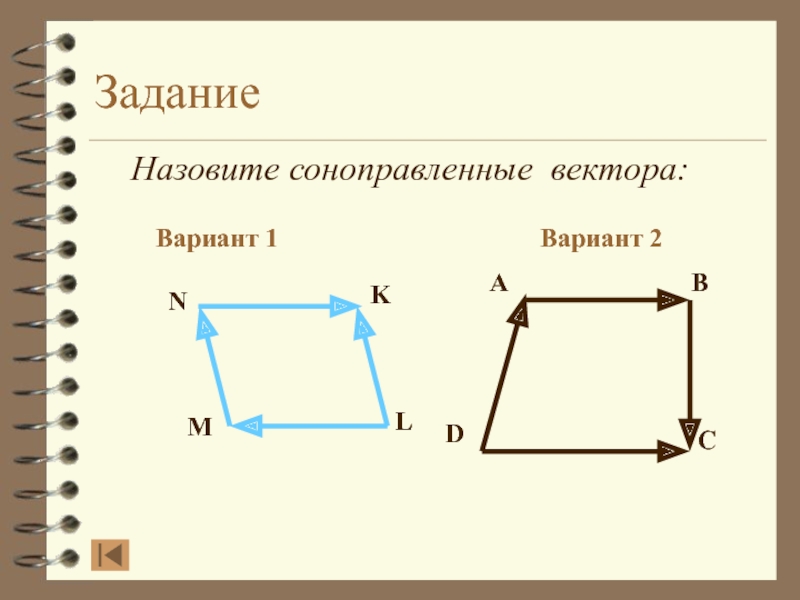
- 16. Задание Назовите соноправленные вектора:Вариант 1Вариант 2ABDCNKLMСравним ответ
- 17. Задание Назовите соноправленные вектора:Вариант 1Вариант 2ABDCNKLM
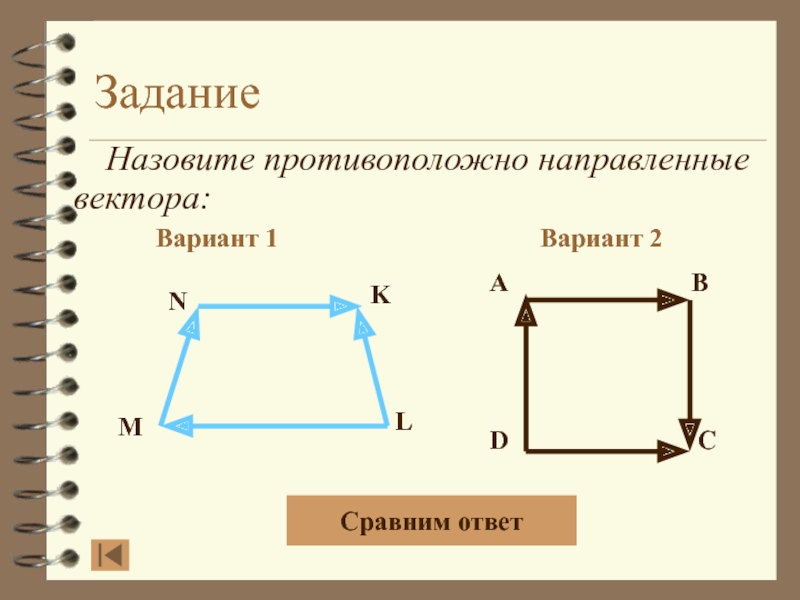
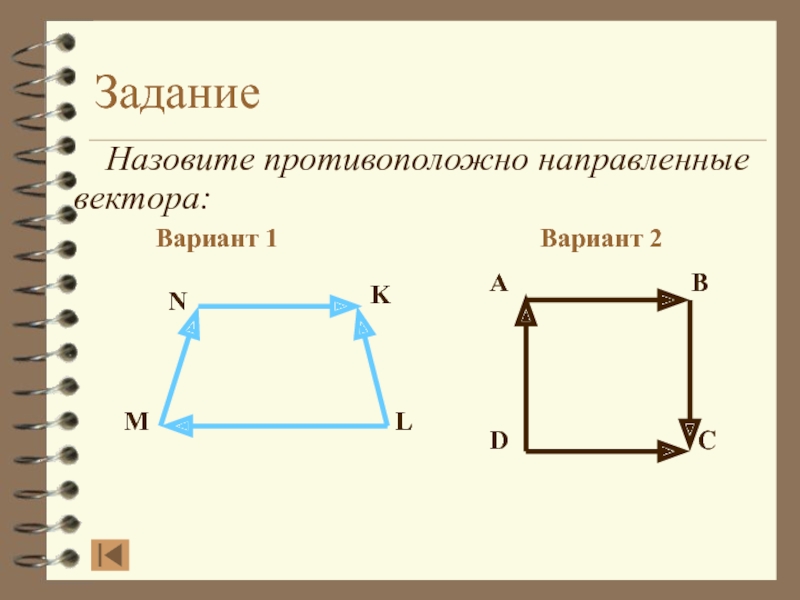
- 18. Задание Назовите противоположно направленные вектора:Вариант 1Вариант 2ABDCNKLMСравним ответ
- 19. Задание Назовите противоположно направленные вектора:Вариант 1Вариант 2ABDCNKLM
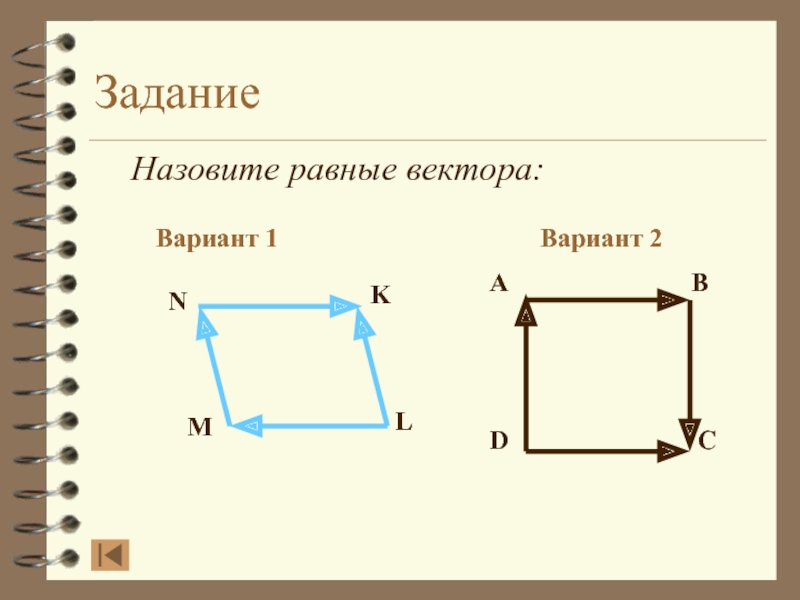
- 20. Задание Назовите равные вектора:Вариант 1Вариант 2Сравним ответ
- 21. Задание Назовите равные вектора:Вариант 1Вариант 2ABDCNKLM
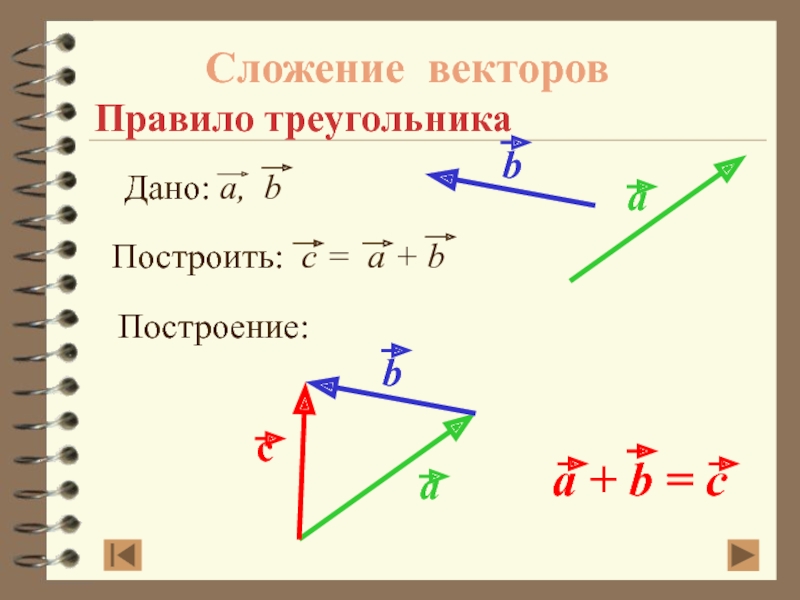
- 22. Сложение векторов Правило треугольникаПостроение:
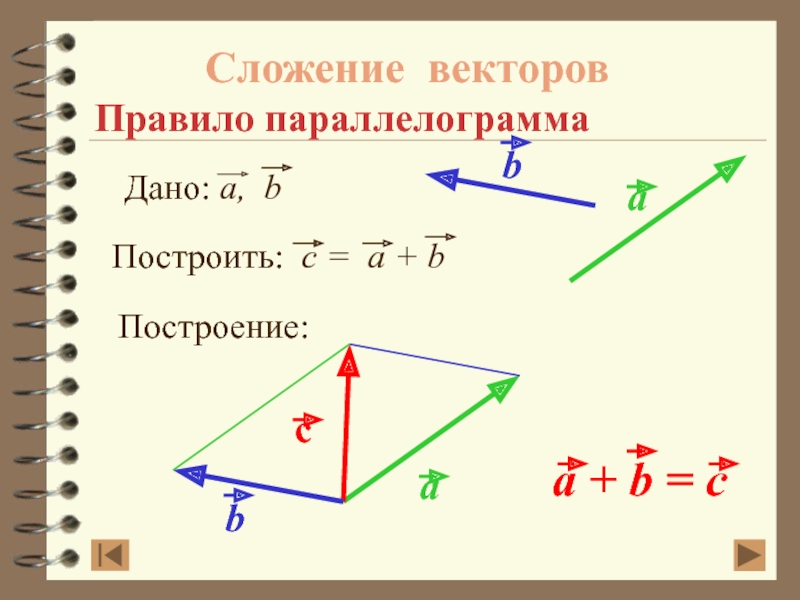
- 23. Сложение векторов Правило параллелограммаПостроение:
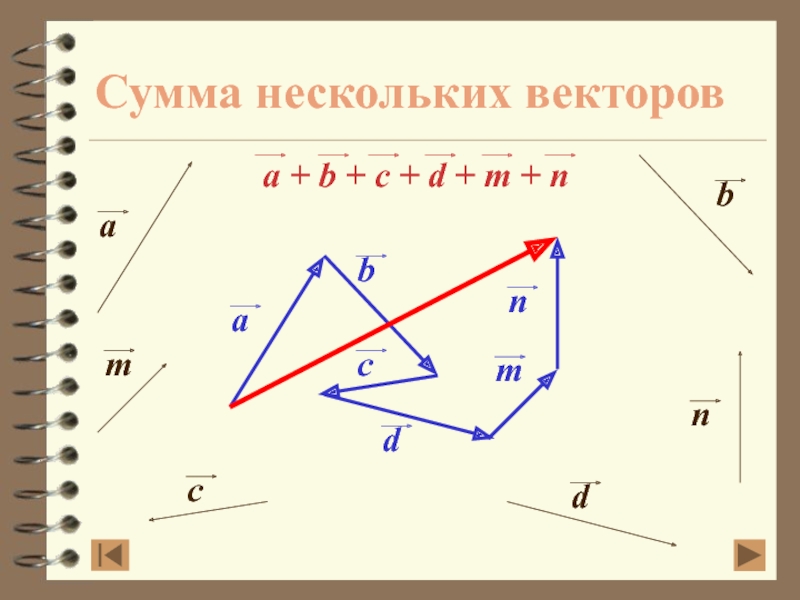
- 24. Сумма нескольких векторов
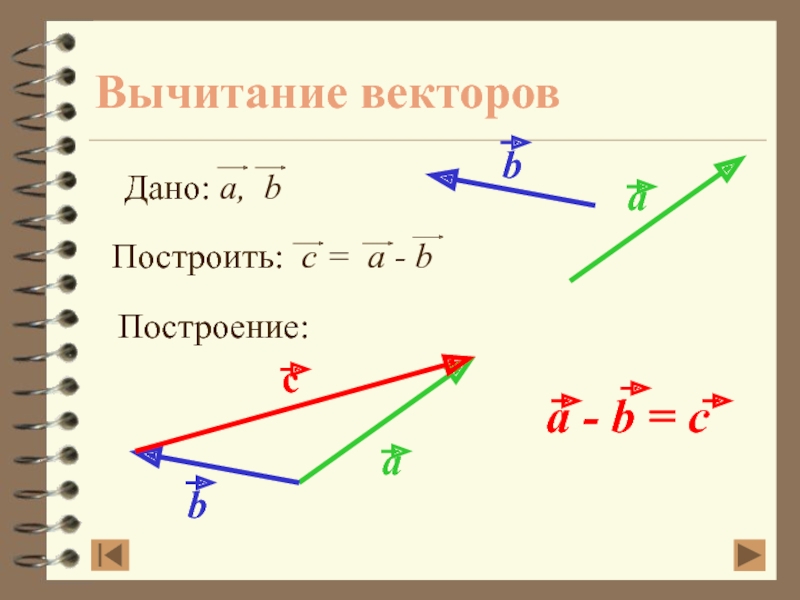
- 25. Вычитание векторовПостроение:
- 26. Умножение вектора a на число kk·a =
- 27. Скачать презентанцию
Понятие вектораМногие физические величины характеризуются числовым значением и направлением в пространстве, их называют векторными величинами
Слайды и текст этой презентации
Слайд 2Понятие вектора
Многие физические величины характеризуются числовым значением и направлением в
пространстве, их называют векторными величинами
Слайд 3Понятие вектора
Отрезок, для которого указано, какая его граничная точка является
началом, а какая - концом, называется направленным отрезком или вектором
Конец
вектораНачало вектора
- вектор
Проверь себя
Слайд 6Длина вектора
Длиной вектора или модулем не нулевого вектора называется длина
отрезка
Проверь себя
Слайд 9Нулевой вектор считается коллинеарным любому вектору
Коллинеарные вектора
Ненулевые вектора называются коллинеарными,
если они лежат на одной прямой или на параллельных прямых
Проверь
себяСлайд 10Сонаправленные вектора
Коллинеарные вектора имеющие одинаковое направление, называются сонаправленными векторами
Проверь себя
Слайд 11Противоположно направленные вектора
Коллинеарные вектора имеющие противоположное направление, называются противоположно направленными
векторами
Проверь себя
Слайд 13Равенство векторов
Векторы называются равными, если они сонаправлены и их длины
равны
Проверь себя
Слайд 18Задание
Назовите противоположно направленные вектора:
Вариант 1
Вариант 2
A
B
D
C
N
K
L
M
Сравним ответ
Слайд 26Умножение вектора a на число k
k·a = b,
|a| ≠ 0,
k – произвольное число
|b| = |k|·|a|,
если k>0, то a
↑↑ bесли k<0, то a ↑↓ b