Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графики основных элементарных функций
Содержание
- 1. Графики основных элементарных функций
- 2. Графики основных элементарных функций Основными элементарными функциями
- 3. .3.4.5.6.
- 4. Показательная функция y = ax
- 5. Тригонометрические функции.y = sin xD(f) = R,
- 6. Обратные тригонометрические функции.y = arcsin xD(f) =
- 7. Гиперболические функции.
- 8. Слайд 8
- 9. Понятие числовой последовательности. Если каждому числу n∈N поставлено
- 10. Примеры.1, 1, 1, … ⇔ хn=1,
- 11. Арифметическая и и геометрическая прогрессии
- 12. Графическое изображение числовой последовательности:точками с координатами (n,
- 13. Определение предела последовательности Число a ∈ R называется
- 14. Геометрический вариант определения предела. Неравенство ⎜хn – a⎜<
- 15. Единственность предела ТЕОРЕМА. Числовая последовательность может
- 16. Ограниченность сходящейся ЧП. ЧП называется ограниченной, если множество
- 17. ТЕОРЕМА. Если числовая последовательность имеет предел, то
- 18. Л ЛЕММА. Если хn→ а при
- 19. Спасибо за внимание!
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 1.2.
Графики основных элементарных функций
Числовая последовательность.
Предел числовой последовательности.
Единственность предела.
Ограниченность сходящейся
числовой последовательности.
Слайд 2Графики основных элементарных функций
Основными элементарными функциями называются функции: постоянная,
степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические.
Всякая функция, которая может
быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и суперпозиций основных элементарных функций, называется просто элементарной функцией.Степенная функция y = xр.
y = x2n, n ∈ N.
D(f) = R, Е(f) = {y≥0}.
y = x2n+1, n ∈ N.
D(f) = R, Е(f) = R
Область определения и график функции зависят от показателя р.
Рассмотрим несколько случаев:
1.
2.
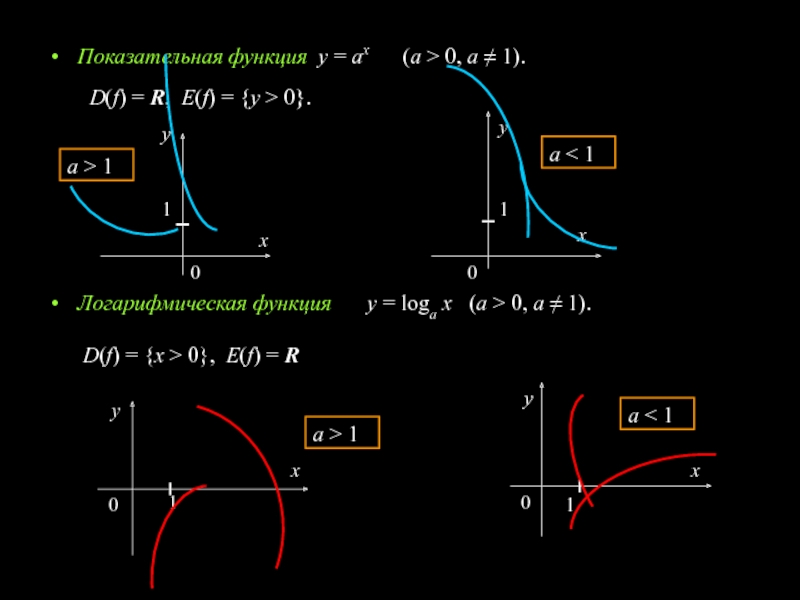
Слайд 4Показательная функция y = ax (a > 0,
a ≠ 1).
Логарифмическая функция y = loga x
(a > 0, a ≠ 1). D(f) = R, Е(f) = {y > 0}.
a > 1
a > 1
a < 1
a < 1
D(f) = {x > 0}, Е(f) = R
Слайд 5Тригонометрические функции.
y = sin x
D(f) = R, Е(f) ={ y ∈ [–1, 1]}.
y
= cos x
D(f) = R, Е(f) ={ y ∈ [–1, 1]}.
y = tg
xD(f) = {x ≠ π/2 + πk, k∈Z}, Е(f) =R
y = ctg x
D(f) = {x ≠ πk, k∈Z}, Е(f) =R
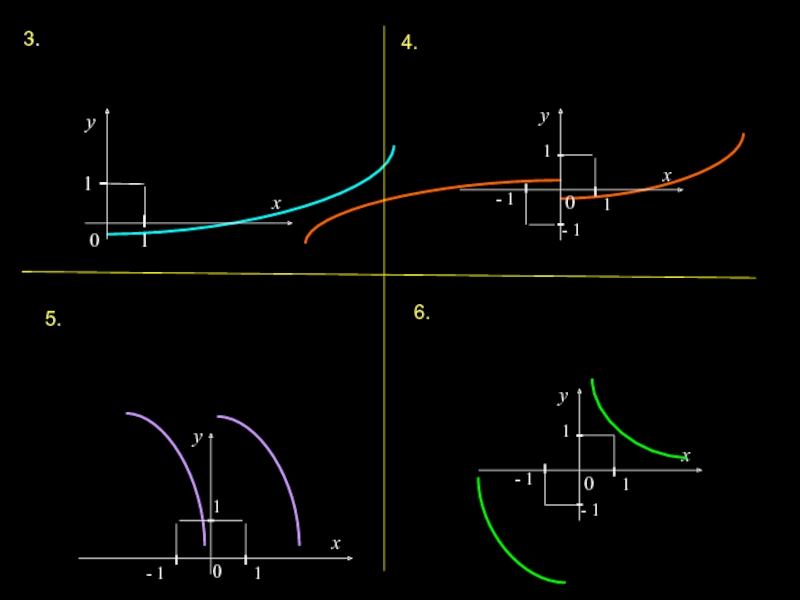
Слайд 6Обратные тригонометрические функции.
y = arcsin x
D(f) = [–1, 1], Е(f) = [–π/2, π/2].
y
= arccos x
D(f) = [–1, 1], Е(f) = [0, π].
y = arctg x
D(f)
= R, Е(f) = (–π/2, π/2).y = arcctg x
D(f) = R, Е(f) = (0, π).
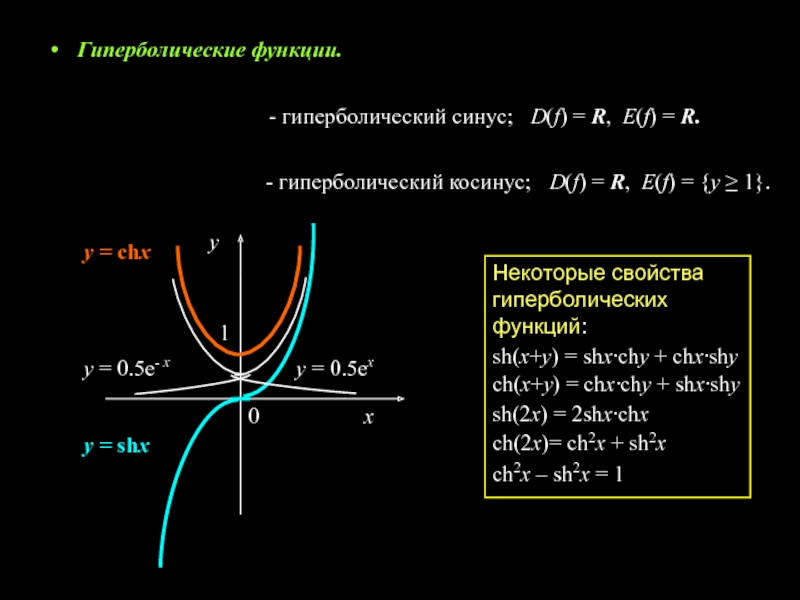
Слайд 7Гиперболические функции.
Некоторые свойства
гиперболических функций:
sh(x+у) = shx·сhу + сhx·shу
сh(x+у) = сhx·сhу + shx·shу
sh(2x) = 2shx·сhx
сh(2x)= сh2x + sh2x
сh2x – sh2x = 1
- гиперболический синус;
- гиперболический косинус;
D(f) = R, Е(f) = {y ≥ 1}.
D(f) = R, Е(f) = R.
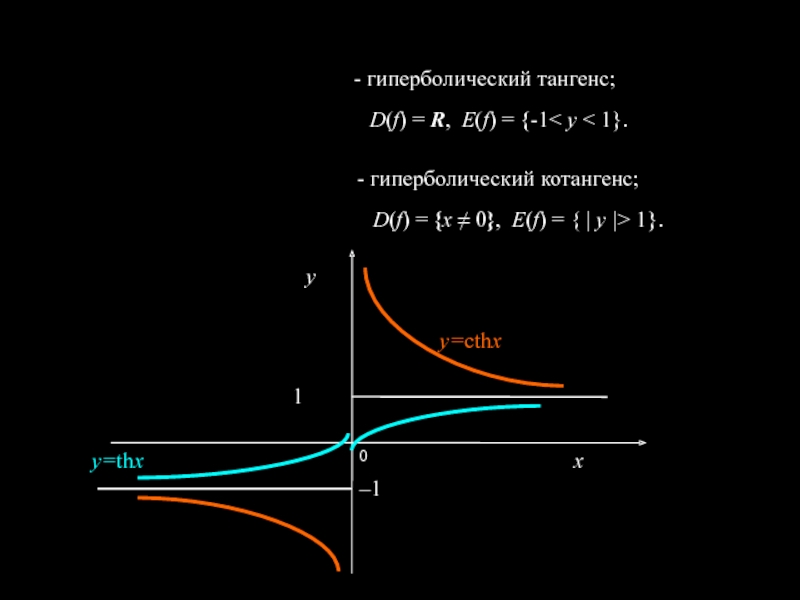
Слайд 8
-
гиперболический тангенс;
- гиперболический котангенс;
D(f) = R, Е(f) = {-1< y
< 1}.D(f) = {x ≠ 0}, Е(f) = { | y |> 1}.
Слайд 9Понятие числовой последовательности.
Если каждому числу n∈N поставлено в соответствие определённое
число хn ∈ R, то полученное упорядоченное множество
х1, х2,
… , хn , … называют числовой последовательностью (ЧП).
Таким образом, числовая последовательность – это функция, областью определения которой является все множество натуральных чисел N. Значения этой функции хn называются элементами последовательности, число n называется номером элемента.
Кратко числовую последовательность обозначают
или {хn} .
Числовая последовательность может быть задана с помощью формулы, позволяющей вычислить каждый элемент последовательности по его номеру.
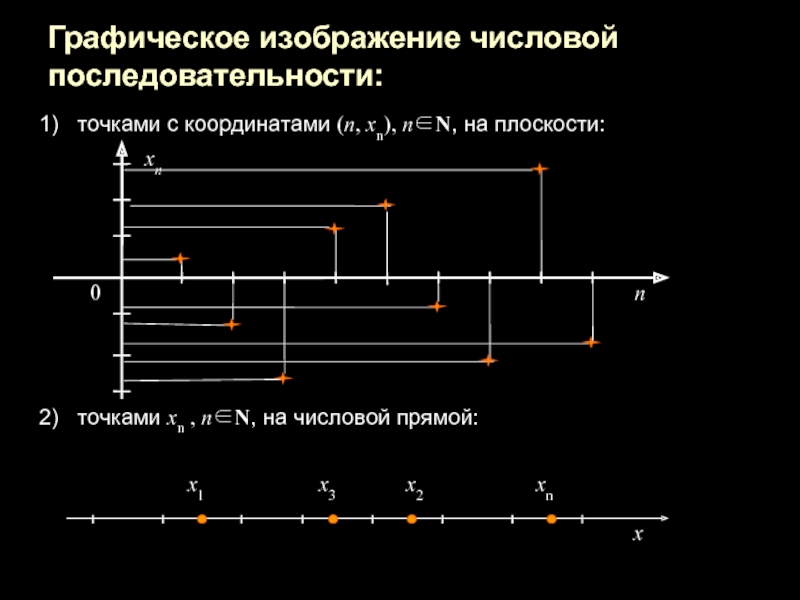
Слайд 12Графическое изображение числовой последовательности:
точками с координатами (n, хn), n∈N, на
плоскости:
точками хn , n∈N, на числовой прямой:
Слайд 13Определение предела последовательности
Число a ∈ R называется пределом (числовой) последовательности
{хn}, если для любого числа ε > 0 найдется такой
номер N(ε) (зависящий от ε), что для всех ее элементов с номерами n ≥ N(ε) выполняется неравенство⎜ хn – a ⎜< ε.
В этом случае пишут
Или по-другому:
Если последовательность имеет предел, то говорят, что она сходится, в противном случае говорят, что она расходится.
С помощью логических символов определение предела последовательности можно записать так:
хn → a при n → ∞.
Слайд 14Геометрический вариант определения предела.
Неравенство ⎜хn – a⎜< ε в определении
предела эквивалентно неравенствам
a – ε < xn < a
+ ε .Другими словами, для любого числа ε > 0 найдется такой номер N(ε), начиная с которого, все члены ЧП принадлежат ε-окрестности точки a.
Число a является пределом ЧП {хn}, если в любой его окрестности содержатся почти все элементы последовательности, за исключением их конечного числа.
Таким образом, вне любой ε-окрестности точки a лежит лишь конечное число элементов ЧП.
Слайд 15Единственность предела
ТЕОРЕМА.
Числовая последовательность может иметь лишь один предел.
Доказательство.
Предположим, что {хn} имеет два предела, причем
а < b. Выберем ε>0 так, чтобы ε-окрестности точек а и b не пересекались:Так как а - предел {хn}, то вне Uε(a) может лежать лишь конечное число элементов ЧП, в частности, интервал Uε(b) может содержать лишь конечное число элементов последовательности. Это противоречит тому, что b – ее предел. Полученное противоречие говорит о том, что числовая последовательность может иметь только один предел.
Слайд 16Ограниченность сходящейся ЧП.
ЧП называется ограниченной, если множество ее значений ограничено
сверху и снизу, т.е.
∃ С1∈R и С2∈R: ∀n∈N ⇒ С1≤
xn ≤ С2.ЧП называется неограниченной, если
∀С > 0 ∃ n∈N: ⎜хn⎜> C.
Примеры.
xn = (–1)n – ограниченная ЧП;
xn = n((–1)n+1 + 1) – неограниченная ЧП.
n
xn
0
Слайд 17 ТЕОРЕМА.
Если числовая последовательность имеет предел, то она ограничена.
Доказательство.
Пусть
Возьмем ε = 1. Согласно определению предела числовой последовательности,
найдется такое N(1), что для всех n ≥ N(1) выполняется неравенство а –1 < xn < а +1.
Пусть
С1= min{x1, x2, … , xN-1, a –1},
C2= max{x1, x2, … , xN-1, a +1}.
Тогда для всех n справедливо неравенство
С1≤ xn ≤ C2 ,
ч.т.д.
Слайд 18 Л
ЛЕММА.
Если хn→ а при n → ∞,
а ≠ 0 и хn ≠ 0 для ∀n, то
числовая последовательность {1/хn} ограничена.Доказательство.
Так как а ≠ 0, то ε = ⎜а⎜/2 > 0. По определению предела для данного ε найдется N(ε)∈N: ∀n≥ N(ε) →
⎜ хn– а ⎜< ⎜а⎜/2.
Воспользуемся свойством модуля вещественного числа:
⎜⎜хn⎜– ⎜а ⎜⎜< ⎜хn– а ⎜< ⎜а⎜/2 ⇒
⎜а⎜/2 < ⎜хn ⎜< 3⎜а ⎜/2 ⇒
1/⎜хn⎜< 2/⎜а ⎜ ∀n ≥ N( ⎜а ⎜/2 ).
Пусть
Тогда для всех n справедливо неравенство
⎜1/хn⎜≤ С,
ч.т.д.


![Графики основных элементарных функций Тригонометрические функции.y = sin xD(f) = R, Е(f) ={ y ∈ [–1, 1]}.y = Тригонометрические функции.y = sin xD(f) = R, Е(f) ={ y ∈ [–1, 1]}.y = cos xD(f) = R, Е(f) ={](/img/thumbs/eab3f7b991c6bf2b50c3ffd7a8f200c7-800x.jpg)
![Графики основных элементарных функций Обратные тригонометрические функции.y = arcsin xD(f) = [–1, 1], Е(f) = [–π/2, π/2].y = Обратные тригонометрические функции.y = arcsin xD(f) = [–1, 1], Е(f) = [–π/2, π/2].y = arccos xD(f) = [–1, 1], Е(f) = [0, π].y](/img/thumbs/d790571ba1a57da89af71835ebdd3ce9-800x.jpg)