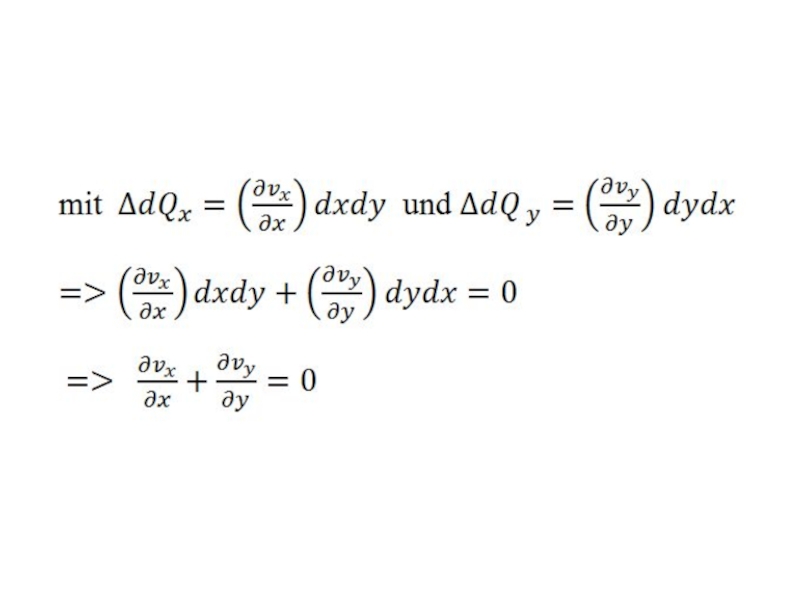Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Hydrodynamik II
Содержание
- 1. Hydrodynamik II
- 2. Volumen- und Massenstrom Volumenstrom V: zeitliche Änderung des Wasservolumens, bzw. Durchfluß Q:Massenstrom:
- 3. KontinuitätsgleichungEs wird eine stationäre inkompressible Strömung in
- 4. Слайд 4
- 5. Die Differentialmasse des Volumens dV ist:
- 6. Der Massenstrom im Stromfaden ist mit v = ds/dt:
- 7. Der Massenstrom in der Stromröhre folgt aus der Integration über den Fließquerschnitt A:
- 8. Da durch die Mantelfläche definitionsgemäß kein Ein-
- 9. Mit (inkompressible Flüssigkeit) folgt:
- 10. In einer Stromröhre ist der Durchfluß
- 11. Anmerkung: Es folgt die Definition der mittleren Geschwindigkeit
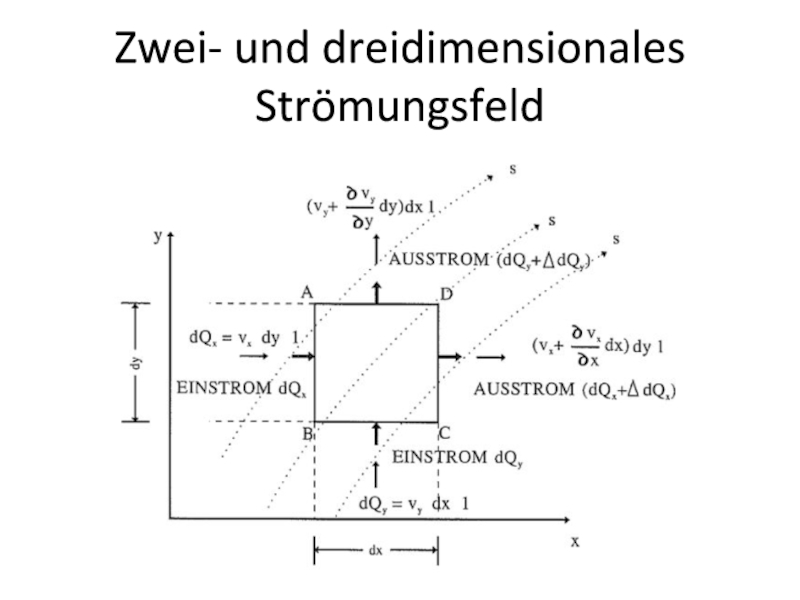
- 12. Zwei- und dreidimensionales Strömungsfeld
- 13. (a) Ausgangssystem und AnnahmenIn einem Strömungsfeld (inkompressible
- 14. (b) Herleitung der KontinuitätsgleichungNach dem Massenerhaltungsgesetz gilt
- 15. Слайд 15
- 16. Dies ist die Koniinuitätsgleichung für eine zweidimensionale
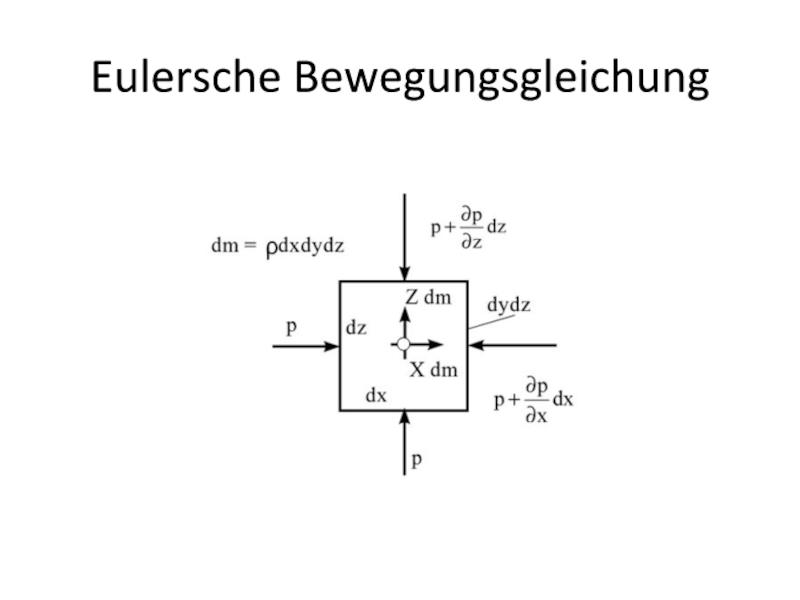
- 17. Eulersche Bewegungsgleichung
- 18. Auf ein prismatisches Flüssigkeitselement wird das Newton'sche
- 19. mit K = {X,Y,Z} ergeben sich für die Komponenten von dF:
- 20. andererseits gilt nach NEWTON: (Newton'sche Kraftgesetz)
- 21. vektoriell zusammengefasst folgt:
- 22. Слайд 22
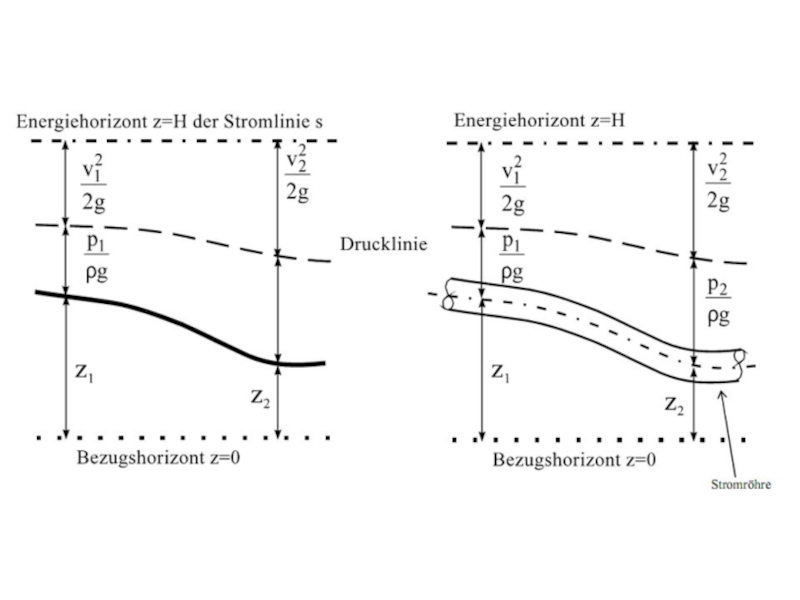
- 23. Die Bernoulli'sche Druck- und Energiegleichung
- 24. Слайд 24
- 25. Satz von Bernoulli: Bei der stationären Bewegung
- 26. Слайд 26
- 27. Wenn v 1 und p1 bekannt ist,
- 28. Слайд 28
- 29. Скачать презентанцию
Volumen- und Massenstrom Volumenstrom V: zeitliche Änderung des Wasservolumens, bzw. Durchfluß Q:Massenstrom:
Слайды и текст этой презентации
Слайд 2
Volumen- und Massenstrom
Volumenstrom V: zeitliche Änderung des Wasservolumens, bzw. Durchfluß
Q:
Слайд 3Kontinuitätsgleichung
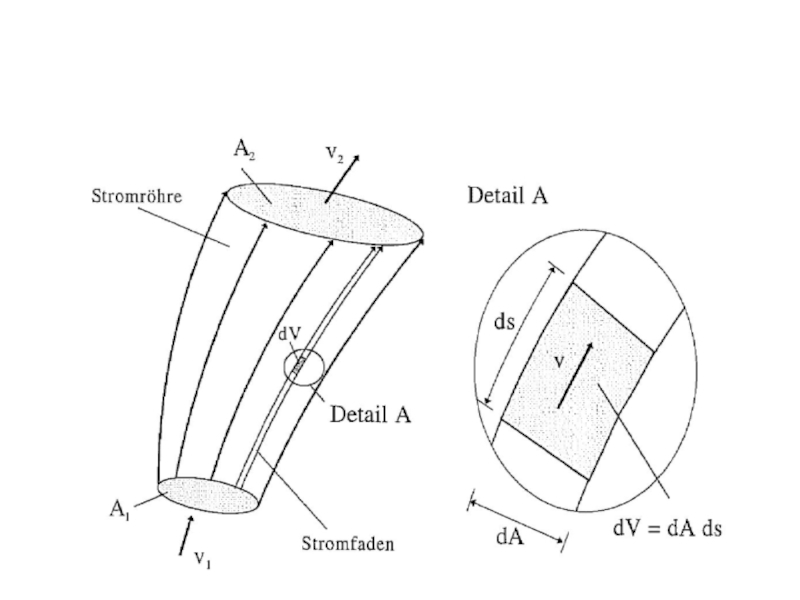
Es wird eine stationäre inkompressible Strömung in einer Stromröhre mit
den Fließ-
querschnitten A1 und A2 und den entsprechenden mittleren Fließgeschwindigkeiten
v1 und v2 betrachtet. In einem Stromfaden wird ein infinitesimales Volumen dV betrachtet:
Слайд 8Da durch die Mantelfläche definitionsgemäß kein Ein- bzw. Ausstrom stattfinden
kann, bleibt der Massenstrom
in jedem Querschnitt der Stromröhre erhalten, d.h. für die Querschnitte A1 und A2 gilt:
Слайд 9Mit
(inkompressible Flüssigkeit)
folgt:
Mit dem Durchfluß
Q = v A folgt schließlich die Konlinuitätsgleichung für eine
stationäre
inkompressible Strömung:Q=v A=konst
Слайд 10 In einer Stromröhre ist der Durchfluß konstant.
oder
Das Verhältnis zweier
querschnittsgemittelter Geschwindigkeiten in dieser Stromröhre ist gleich dem umgekehrten Verhältnis
der zu ihnen gehörenden Fließquerschnitte.
Слайд 13(a) Ausgangssystem und Annahmen
In einem Strömungsfeld (inkompressible Flüssigkeit, ρ= konst.)
wird ein finites Kontrollvolumen ABCD mit der Einheitsbreite 1 senkrecht
zur x-y Ebene betrachtet
Слайд 16Dies ist die Koniinuitätsgleichung für eine zweidimensionale inkompressible
Strömung (stationärer und
instationärer Fall).
Entsprechend gilt für eine dreidimensionale Strömung:
Слайд 18Auf ein prismatisches Flüssigkeitselement wird das Newton'sche Kraftgesetz F =
m a angewandt.
dF ist im Falle der idealen Flüssigkeit gleich
der Summe der Massenkräfte K und der Kräfte infolge des Flüssigkeitsdruckes p; 
Слайд 25Satz von Bernoulli:
Bei der stationären Bewegung einer idealen, nur
der Schwere als Massenkraft unterworfenen Flüssigkeit ist für alle Punkte
einer Stromlinie die Summe aus Geschwin-digkeits-, Druck- und Ortshöhe konstant. Diese Konstanz betrifft aber nur eine Stromlinie.
Слайд 26 wird auch als
Druckhöhe bezeichnet und auch als solche aufgetragen
Die Druckhöhe stellt die
Höhe derjenigen Flüssigkeitssäule dar, deren Gewicht - bezogen auf die Flächeneinheit - gerade den Druck p = p .g .h erzeugt, p wird meist als statischer Druck bezeichnet.
Слайд 27Wenn v 1 und p1 bekannt ist, kann v2 und
p2 berechnet werden. Dazu ist aber noch eine Gleichung, die
Kontinuitätsgleichung, erforderlich, wobei wieder ein Übergang von einer Stromlinie auf eine Stromröhre erfolgt.
