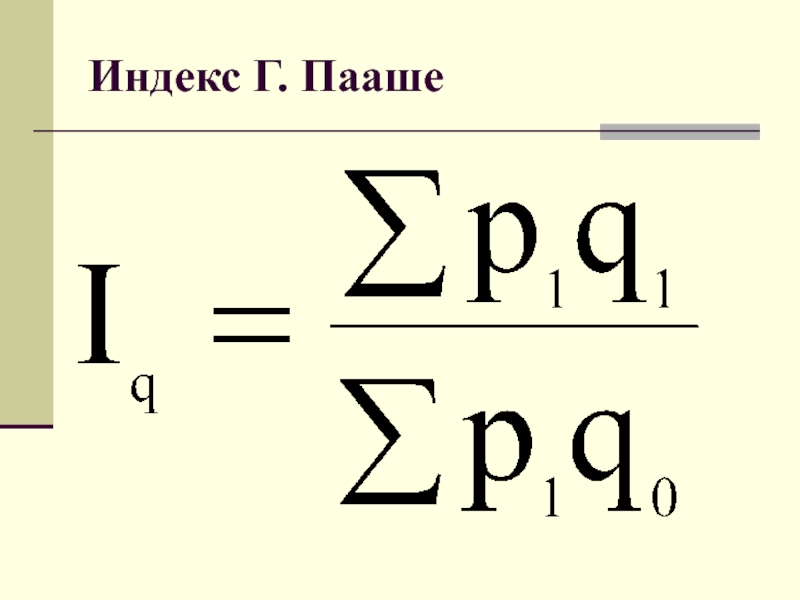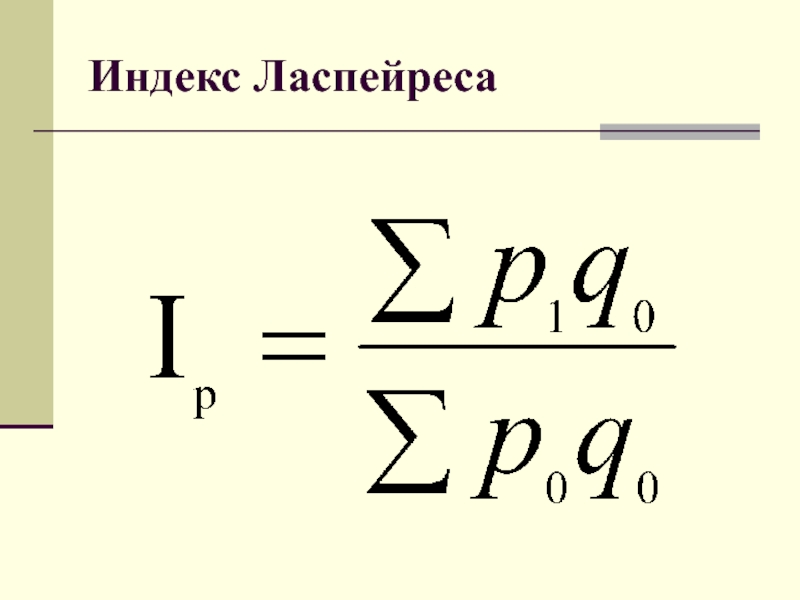Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Индексы
Содержание
- 1. Индексы
- 2. Индекс представляет собой относительную величину, получаемую в
- 3. Индексируемая величина величина, изменение которой изучается в данном конкретном случае с помощью индекса
- 4. Способы построения индексов.
- 5. Каждая индексируемая величина имеет свое символическое обозначение:Количество
- 6. Индивидуальные индексыхарактеризуют изменение только одного элемента совокупности
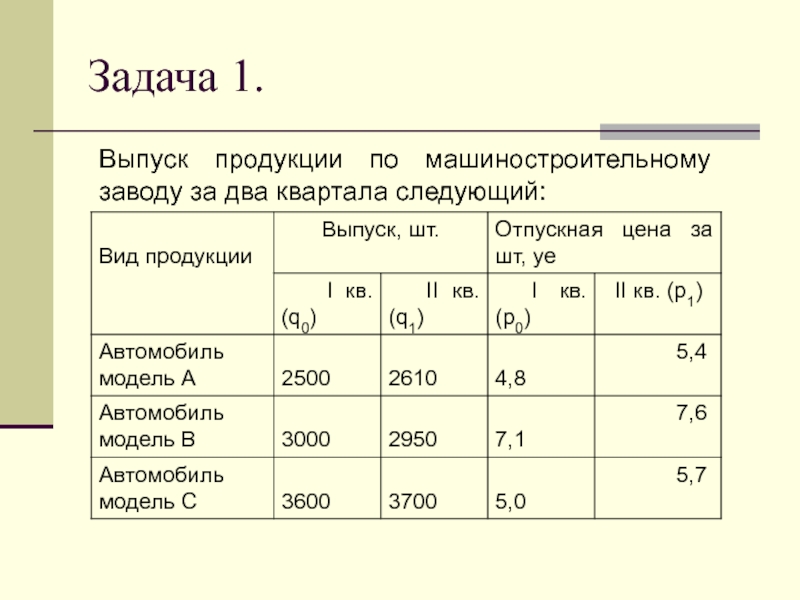
- 7. Задача 1.Выпуск продукции по машиностроительному заводу за два квартала следующий:
- 8. Задача 1. Определить: изменение (в %) выпуска
- 9. Задача 1.Производство автомобиля С в отчетном году выросло на 2,8% по сравнению с прошлым годом.
- 10. Задача № 1 Определить изменение цен (
- 11. Задача 1Автомобиль модели В
- 12. Задача 1Автомобиль модели С
- 13. Сводный индекс отражает изменение по всей совокупности
- 14. Индекс стоимости продукции (товарооборота).
- 15. показывает абсолютное изменение общей стоимости продукции за счет изменения количества продукции и цен.
- 16. Задача 1. Определить изменение товарооборота в целом
- 17. Агрегатные индексы Индексы количественных показателей.Индексы качественных показателей
- 18. Внешняя отличительная особенность агрегатного индекса В числителе
- 19. Индекс физического объема товарооборота.Если мы хотим узнать
- 20. Индекс Э. Ласпейреса
- 21. эта разность показывает абсолютное изменение общей стоимости продукции за счет изменения количества продукции
- 22. Индекс Г. Пааше
- 23. Сравнение индекса Ласпейреса и индекса ПаашеИндекс Ласпейреса:В
- 24. Задача 1. Определить изменение выпуска продукции в
- 25. Индексы качественных показателей:Агрегатный индекс цен Индексируемой величиной
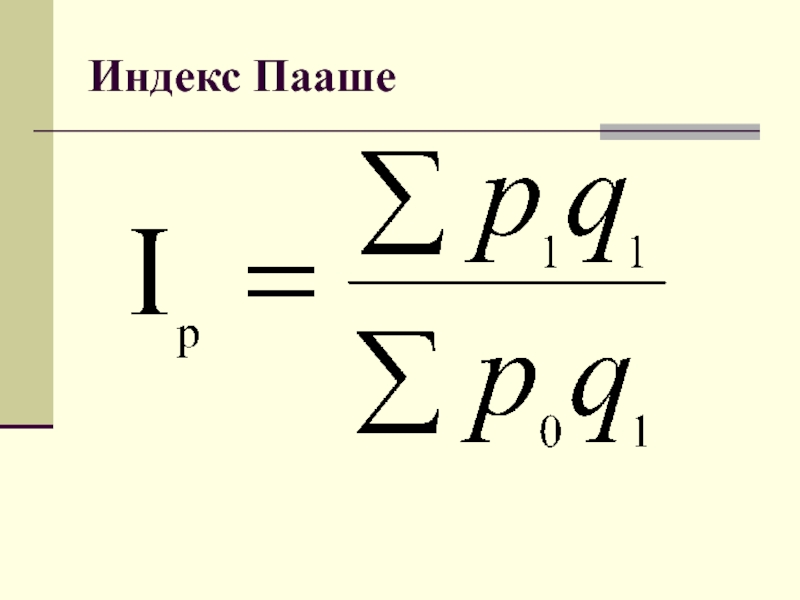
- 26. Индекс Пааше
- 27. Абсолютное изменение всей стоимости продукции за счет изменения цен.
- 28. Индекс Ласпейреса
- 29. Сравнение индекса цен Пааше и ЛаспейресаИндекс ПаашеВ
- 30. Задача1. Определить среднее изменение цен по всему
- 31. Цепные и базисные индексы.Произведение цепных индивидуальных индексов
- 32. Задача 4 По фирме имеются следующие данные
- 33. Задача 4Расчитаем цепные индексы:
- 34. Задача № 4.Расчитаем базисные индексы
- 35. Произведение цепных индексов равно базисному 1,114*1,119 = 1,2465
- 36. Вывод: на предприятии в 2005 году по
- 37. Цепные индивидуальные индексы
- 38. Базисные индивидуальные индексы
- 39. Связь индивидуальных цепных и базисных индексов.
- 40. Расчеты с помощью индексных систем недостающих индесов.или Iр * Iq = Ipq
- 41. Задача № 8. Как изменились цены, если
- 42. Расчет средних арифметических индексов.Агрегатный индекс физического объема
- 43. Слайд 43
- 44. Средний гармонический индекс ценесли в качестве исходных
- 45. Получим средний гармонический индекс цен
- 46. Индексы структурных сдвигов Индекс переменного состава представляет
- 47. На изменение признака влияет два фактора:изменения значений
- 48. Индекс постоянного (фиксированного) составаотражает изолированное действие первого
- 49. Индекс структурных сдвиговхарактеризует влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака:
- 50. Связь индексов переменного, постоянного состава и структурных
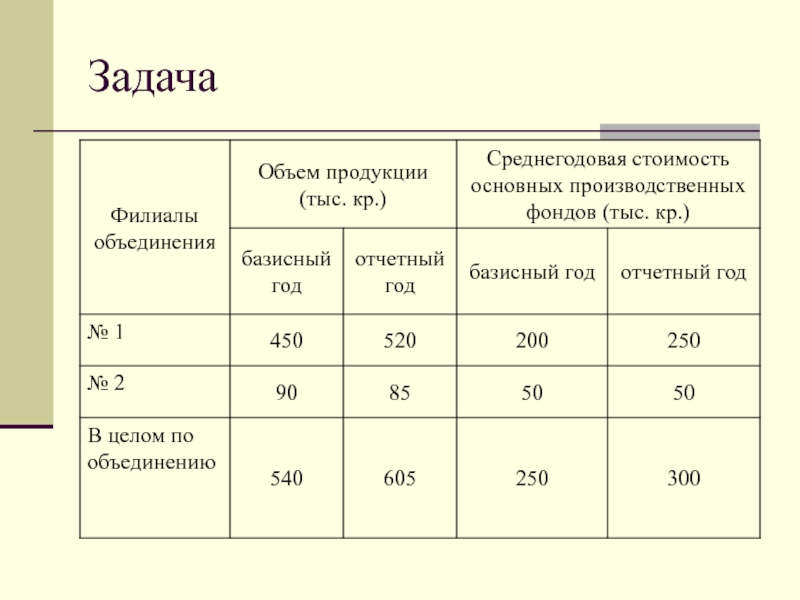
- 51. Задача
- 52. Необходимо определить:уровни фондоотдачи в отдельных филиалах объединения
- 53. Фондоотдача обобщающий показатель, характеризующий уровень использования производственных
- 54. Где f - уровень фондоотдачи Q - объем выпускаемой продукции F - среднегодовая стоимость фондов.
- 55. Вычислим фондоотдачу для каждого филиала в отчетном и базисном периодах
- 56. Средний по объединению уровень фондоотдачи в базисном и отчетном периоде:
- 57. Динамика среднего по объединению уровня фондоотдачи:индекс переменного
- 58. Выявим раздельное влияние каждого из факторов:уменьшение фондоотдачи в отдельных филиалахструктурные изменения в распределении фондов между филиалами
- 59. Таким образом, фондоотдача в среднем по филиалам
- 60. Проверим увязку индексов в систему
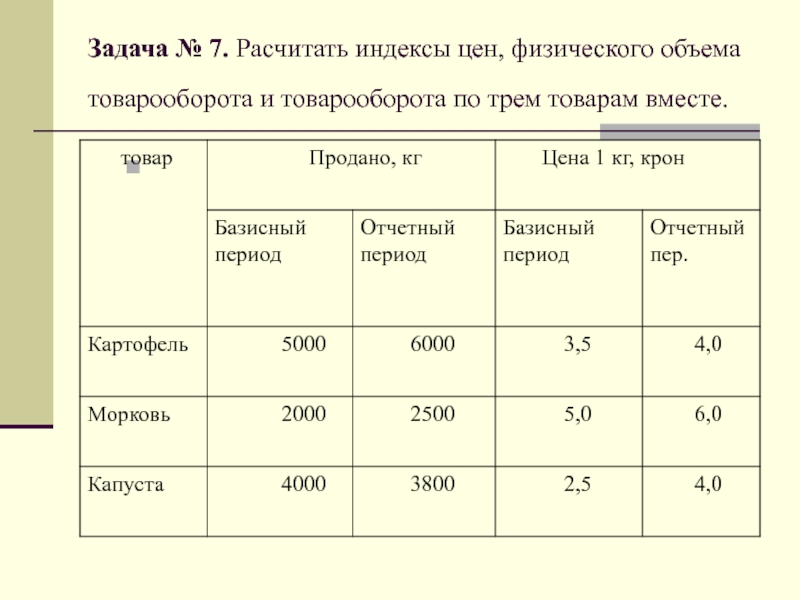
- 61. Задача № 7. Расчитать индексы цен, физического
- 62. Задача № 7. Решение:
- 63. Скачать презентанцию
Индекс представляет собой относительную величину, получаемую в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве или по сравнению с планом.
Слайды и текст этой презентации
Слайд 2Индекс
представляет собой относительную величину, получаемую в результате сопоставления уровней
Слайд 3Индексируемая величина
величина, изменение которой изучается в данном конкретном случае
с помощью индекса
Слайд 5Каждая индексируемая величина имеет свое символическое обозначение:
Количество единиц данного вида
продукции - q
Цена единицы изделия - p
Себестоимость единицы изделия -
z Трудоемкость единицы изделия - t
Слайд 8Задача 1. Определить: изменение (в %) выпуска каждого вида продукции
Производство автомобиля А в отчетном году по сравнению с прошлым
годом составило 104,4%, т.е. возросло на 4,4%Производство автомобиля В – составило 98,3%, т.е. снизилось на 1,7%
Слайд 9Задача 1.
Производство автомобиля С в отчетном году выросло на 2,8%
по сравнению с прошлым годом.
Слайд 10Задача № 1 Определить изменение цен ( в %) по
каждому виду продукции
Автомобиль модели А
или 112,5%следовательно цена повысилась на
12,5% (112,5-100)
Слайд 13Сводный индекс
отражает изменение по всей совокупности элементов сложного явления
Если индексы охватывают не все элементы сложного явления, а лишь
часть, то их называют групповыми или субиндексами.Обозначаются сводные индексы I
Слайд 15
показывает абсолютное изменение общей стоимости продукции за счет изменения количества
продукции и цен.
Слайд 16Задача 1. Определить изменение товарооборота в целом по предприятию.
Общая стоимость
произведенной продукции увеличилась на 12,3% (112,3% - 100%). Это привело
к росту товарооборота на сумму:57604 – 51300 = 6304 у.е.
Слайд 18Внешняя отличительная особенность агрегатного индекса
В числителе и в знаменателе
меняется индексируемая величина.
Значения другой, являющейся соизмерителем, остаются неизменными
Слайд 19Индекс физического объема товарооборота.
Если мы хотим узнать как на стоимость
проданной продукции повлияло изменение количества проданных товаров, то необходимо устранить
(элиминировать) влияние изменения цен.Слайд 21
эта разность показывает абсолютное изменение общей стоимости продукции за счет
изменения количества продукции
Слайд 23Сравнение индекса Ласпейреса и индекса Пааше
Индекс Ласпейреса:
В качестве коэффициента соизмерения
используются цены базисного периода
Индекс Пааше
В качестве коэффициента соизмерения используются цены
отчетного периода или сопоставимые (фиксированные) ценыСлайд 24Задача 1. Определить изменение выпуска продукции в целом по предприятию.
Изменение
количества произведенных автомобилей привело к росту стоимости произведенной продукции на
1,4% (101,4% - 100%)При этом товарооборот вырос на 784 у.е. (57604 – 56820)
Слайд 25Индексы качественных показателей:
Агрегатный индекс цен
Индексируемой величиной в данном случае
является цена (р), количество продукции (q) носит название веса.
Слайд 29Сравнение индекса цен Пааше и Ласпейреса
Индекс Пааше
В качестве веса используется
количество товара отчетного периода
Индекс Ласпейреса
В качестве веса используется количество товара
базисного периодаРекомендуется для характеристики среднего изменения цен на потребительские товары
Слайд 30Задача1. Определить среднее изменение цен по всему ассортименту продукции.
Среднее изменение
цен по всему ассортименту продукции
Таким образом цены на продукцию
предприятия повышены в среднем на 10,8%, за счет чего стоимость продукции повысилась на 5520 уе ( 56820- 51300)Слайд 31Цепные и базисные индексы.
Произведение цепных индивидуальных индексов равно последнему базисному:
Базисный
агрегатный индекс может быть получен как произведение цепных агрегатных индексов
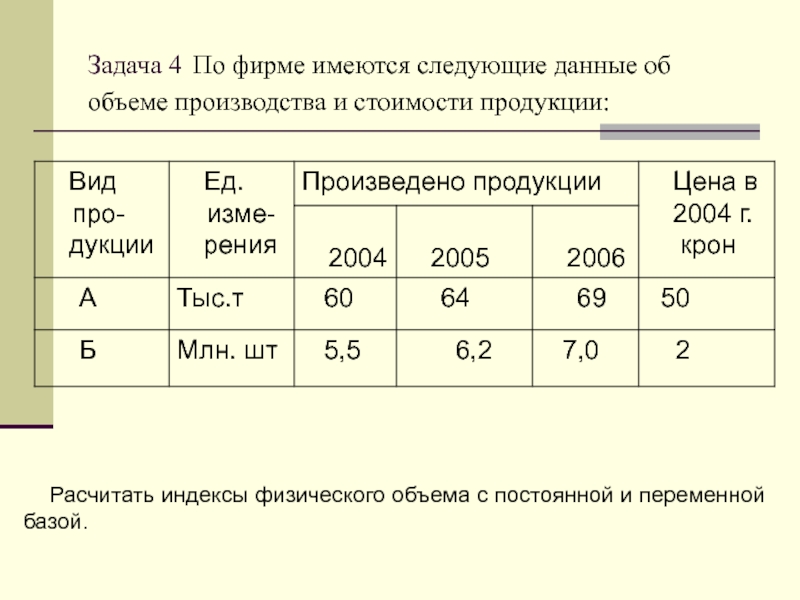
при постоянных соизмерителяхСлайд 32Задача 4 По фирме имеются следующие данные об объеме производства
и стоимости продукции:
Расчитать индексы физического объема с постоянной и
переменной базой.Слайд 36Вывод:
на предприятии в 2005 году по сравнению с 2004
годом наблюдается рост производства за счет увеличения количества выпускаемой продукции
на 1,114 * 100% = 111,4% - 100% = 11,4%;В 2006 г. по сравнению с 2004 г также наблюдается рост производства, который составил 1,246*100% - 100% = 24,6%. Причиной такого роста является увеличение количества выпущенных изделий
В 2006 г по сравнению с 2005 г рост объема производства за счет увеличения количества изделий А и Б составил 1,119*100% - 100% = 11,9%
Слайд 41Задача № 8. Как изменились цены, если физический объем товарооборота
увеличился на 12%, а товарооборот вырос на 9%?
Iq = 100%
+ 12% = 112%Ipq = 100% + 9% = 109%
97,3% - 100% = -2,7%
Т.е. цены снизились на 2,7%
Слайд 42Расчет средних арифметических индексов.
Агрегатный индекс физического объема имеет вид
Если из
условия известна стоимость произведенной или проданной продукции
а также изменение количества произведенной или проданной продукции Слайд 44Средний гармонический индекс цен
если в качестве исходных данных имеем
и изменение цен, т.е.
Тогда
заменяя
в формуле агрегатного индекса цен Слайд 46Индексы структурных сдвигов
Индекс переменного состава представляет собой соотношение средних
уровней изучаемого явления, относящихся к разным периодам:
Слайд 47На изменение признака влияет два фактора:
изменения значений осредняемого признака (x)
у отдельных единиц совокупности;
структурных изменений, под которыми понимается изменение доли
отдельных единиц совокупности в общей их численности (d=f / f).Слайд 48Индекс постоянного (фиксированного) состава
отражает изолированное действие первого фактора
Индекс постоянного
состава может быть рассчитан и в агрегатной форме:
Слайд 49Индекс структурных сдвигов
характеризует влияние изменения структуры изучаемой совокупности на динамику
среднего уровня признака:
Слайд 50Связь индексов переменного, постоянного состава и структурных сдвигов
Индексы переменного, постоянного
состава и структурных сдвигов увязываются в следующую систему:
Слайд 52Необходимо определить:
уровни фондоотдачи в отдельных филиалах объединения в отчетном и
базисном периодах;
средний уровень фондоотдачи в целом по объединению в отчетном
и базисном периодах;изменение среднего по объединению уровня фондоотдачи в отчетном периоде по сравнению с базисным, в том числе за счет: а) изменения уровня фондоотдачи в отдельных филиалах; б) структурных изменений.
Слайд 53Фондоотдача
обобщающий показатель, характеризующий уровень использования производственных фондов. Отдача основных
производственных фондов рассчитывается путем деления объема выпущенных за определенный период
продукции на среднюю за этот период стоимость основных производственных фондов.Слайд 54
Где f - уровень фондоотдачи
Q - объем выпускаемой продукции
F - среднегодовая стоимость фондов.
Слайд 57Динамика среднего по объединению уровня фондоотдачи:
индекс переменного состава
или 93,5%, т.е.
фондоотдача снизилась на 6,5% под влиянием двух факторов:
1) уменьшения фондоотдачи
в отдельных филиалах и 2)структурных изменений в распределении фондов между филиалами.
Слайд 58Выявим раздельное влияние каждого из факторов:
уменьшение фондоотдачи в отдельных филиалах
структурные
изменения в распределении фондов между филиалами
Слайд 59Таким образом, фондоотдача в среднем по филиалам объединения снизилась на
7,3%, что привело к аналогичному снижению среднего уровня фондоотдачи в
целом по объединению.Структурные изменения, а именно увеличение доли фондов первого филиала, который характеризуется более эффективным уровнем их использования, обусловили рост среднего уровня фондоотдачи по объединению на 0,9%.