Слайд 1ГЛАВА 1
ОСНОВЫ КИНЕМАТИКИ
1.1 Пространственно-временные системы отсчеты. Постулаты классической механики
Слайд 2Относительность движения
Механическим движением называется изменение положения тела в пространстве с
течением времени.
Положение тела, а также его движение в пространстве может
быть определено только по отношению к другим телам. В связи с этим необходимо ввести понятие системы отсчета.
Тело отсчета – это тело (или система тел), относительно которого определяется положение в пространстве интересующего нас объекта.
Слайд 3Система координат
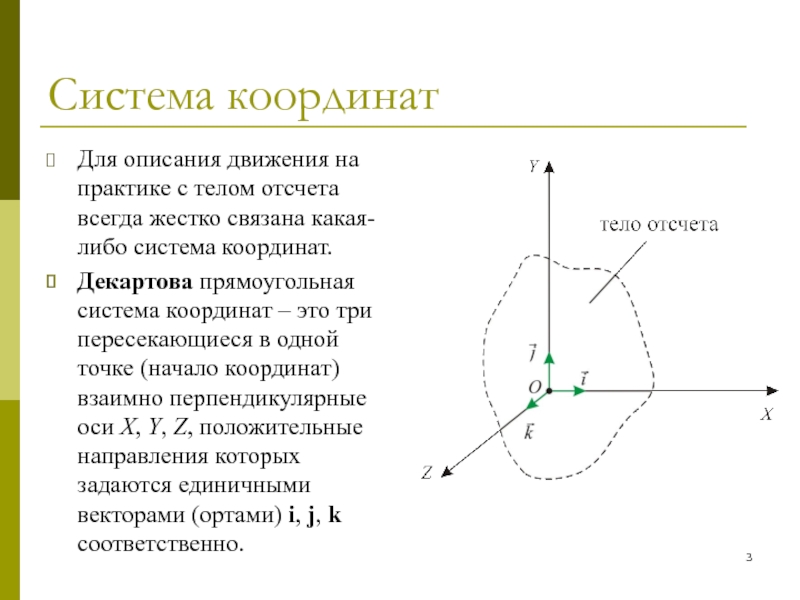
Для описания движения на практике с телом отсчета всегда
жестко связана какая-либо система координат.
Декартова прямоугольная система координат – это
три пересекающиеся в одной точке (начало координат) взаимно перпендикулярные оси X, Y, Z, положительные направления которых задаются единичными векторами (ортами) i, j, k соответственно.
Слайд 4Координаты тела
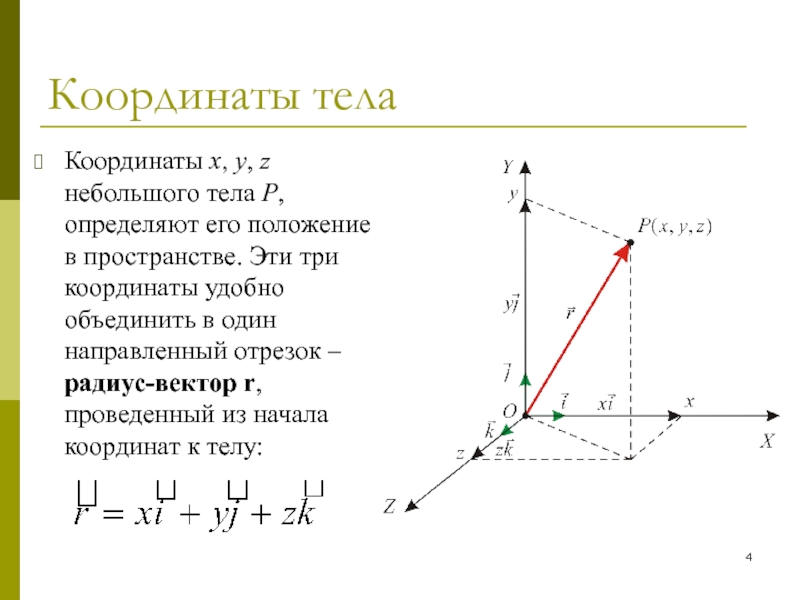
Координаты x, y, z небольшого тела P, определяют его
положение в пространстве. Эти три координаты удобно объединить в один
направленный отрезок – радиус-вектор r, проведенный из начала координат к телу:
Слайд 5Измерение длины
Определение координат тела в конечном счете сводится к измерению
расстояний (длин отрезков).
Под измерением длины будем понимать следующую операцию. Некоторый
твердый стержень принимается за эталон, а его длина – за единицу длины.
При измерении расстояния между точками (или длины тела) определяется число, показывающее, сколько раз в отрезке, проходящей через эти точки прямой укладывается выбранный нами эталон. Это число и называется расстоянием или длиной отрезка. Если число не целое, предварительно длину эталона делят на более мелкие части.
Слайд 6Измерение длины
Инструментом для измерения длины может служить, например, линейка с
нанесенной на нее миллиметровой шкалой (простейший эталон).
При измерении очень малых
длин (физика атомов и молекул) применяются методы электронной микроскопии, туннельной и атомно-силовой микроскопии; при измерении расстояний до удаленных объектов – оптические методы и т.д.
Однако принципиальный способ измерения длины отрезка всегда сводится к его сравнению с эталоном.
Слайд 7Измерение длины
За единицу СИ (Международная система единиц) принят метр (м).
Первоначально
(с 1799 г.) за эталон метра принимался платиновый прототип метра
в виде линейки ширины 25 см и толщины 4 мм с расстоянием между концами 1 м, причем метр был определен как 1/10000000 часть земного меридиана.
С конца XIX до середины XX в. Международный эталон метра был реализован в виде стержня из платиново-иридиевого сплава.
Начиная с 1983 г. метр определяется как длина пути, проходимая в вакууме плоской электромагнитной волной за 1/299792458 долю секунды.
Слайд 8Измерение времени
Движение тел происходит в пространстве и во времени. Для
его описания необходимо измерять также и промежутки времени. Это делают
с помощью часов.
Под часами понимают любое устройство, в котором совершается пригодный для измерения времени периодический процесс (например, колебания маятника с постоянной амплитудой, движение Земли вокруг собственной оси, колебания электромагнитного поля и др.).
За единицу времени в СИ принята секунда (с). Эталон секунды – промежуток времени, в течение которого совершается 9192631770 колебаний электромагнитного излучения, соответствующего переходу между определенными сверхтонкими энергетическими уровнями основного состояния атома 133Cs в отсутствие внешних полей.
Слайд 9Синхронизация часов
Для описания механического движения необходимо пользоваться единым для всего
пространства временем и, следовательно синхронизировать размещенные в различных его частях
часы, т.е. установить их так, чтобы они показывали одинаковое время.
Это легче сделать с помощью световых импульсов. Из пункта A посылается в пункт B световой импульс, который, отразившись от расположенного в пункте B зеркала, возвращается в A. Полагают, что скорости распространения из пункта A в пункт B световых сигналов одинаковы. Пусть t – время на расположенных в пункте A часах в момент отправления сигнала; τ - время распространения сигнала от A до B и обратно, измеренное по тем же часам. Тогда на часах в пункте B в момент прихода в этот пункт светового сигнала следует установить время t + τ/2.
Слайд 10Пространственно-временная
система отсчета
Мы установили, что для описания движения в пространстве
и во времени необходимо иметь:
тело отсчета и связанную с ним
систему координат;
прибор для измерения длин отрезков (линейку);
устройство для измерения промежутков времени (часы);
метод синхронизации часов.
Совокупность перечисленных условий образует т.н. пространственно-временную систему отсчета.
Слайд 11Постулаты классической механики о пространстве, времени и движении
В классической ньютоновской
механике размеры тел и промежутки времени между событиями рассматриваются как
абсолютные величины. Это означает, что можно говорить о длине тела, не указывая, покоится это тело или движется в данной системе отсчета. Можно также говорить об одновременности событий, не указывая, в какой системе отсчета эти события описываются.
Другими словами, линейные масштабы (длины отрезков) и промежутки времени остаются неизменными при переходе от одной системы отсчета к другой, т.е. не зависят от выбора системы отсчета.
Эти представления отражают т.н. ньютоновскую концепцию абсолютности пространства и времени
Слайд 12Постулаты классической механики о пространстве, времени и движении
Опыт показывает, что
предположения (постулаты) об абсолютности пространства и времени являются справедливыми до
тех пор, пока скорости тел малы по сравнению со скоростью света в вакууме: c ≈ 3 · 108 м/с.
При переходе к скоростям, сравнимым со скоростью света, характер движения тел изменяется. События, одновременные в одной системе отсчета, могут оказаться неодновременными в другой системе. Понятие одновременности событий является относительным. Аналогично, размеры движущихся с большими скоростями тел меняются при переходе от одной системы отсчета к другой.
Механика, основанная на представлениях об относительности линейных масштабов и промежутков времени, называется релятивистской.
Слайд 13ГЛАВА 1
ОСНОВЫ КИНЕМАТИКИ
1.2 Векторный способ описания движения материальной точки
Слайд 14Кинематика. Выбор системы отсчета
Кинематика – это раздел механики, в котором
изучают способы описания движения тел, не интересуясь порождающими это движение
причинами
В разных системах отсчета (далее – СО) движение одного и того же тела выглядит по-разному. В кинематике при выборе СО руководствуются только соображениями удобства, т.к. никаких отличий одной СО по сравнению с другой не существует. Т.о., в кинематике все системы отсчета равноправны.
Рассматривая движение тел на Земле (или вблизи нее), естественно связать СО с Землей. Изучая движение самой Земли, СО удобнее связать с Солнцем и т.д.
Слайд 15Понятие материальной точки
Реальные движения тел весьма сложны. Чтобы отвлечься от
несущественных для данного движения деталей, используются идеализированные модели, применимость которых
зависит:
от конкретного характера данной задачи;
от степени точности полученного результата.
Материальная точка (или частица) – это
макроскопическое тело, размеры которого малы по
сравнению с характерными для изучаемого движения
масштабами.
Слайд 16Понятие материальной точки
Произвольное макроскопическое тело, размеры которого возможно не малы,
по сравнению с характерными для данной задачи расстояниями, можно мысленно
разбить на малые макроскопические части, взаимодействующие между собой, и каждую из них принять за материальную точку.
Тогда движение произвольного тела сводится к движению системы взаимодействующих между собой материальных точек (частиц).
Слайд 17Векторный способ задания движения
Рассмотрим движение частицы A в некоторой выбранной
СО, начало координат которой расположено в точке O.
Положение точки A
в пространстве при векторном способе задания движения задается радиусом-вектором r, проведенным из начала координат к частице. В процессе движения радиус-вектор r меняется как по модулю, так и по направлению, т.е. представляет собой векторную функцию времени:
Слайд 18Траектория. Перемещение
Траектория – это линия в пространстве, вдоль которой движется
частица (геометрическое место концов радиуса-вектора частицы).
Пусть за промежуток времени Δt
= t2 – t1 частица переместилась из точки 1 в точку 2.
Перемещением Δr = r2 – r1 за промежуток времени Δt называется вектор, проведенный из начального в конечное положение частицы (из точки 1 в точку 2).
Слайд 19Вектор средней скорости
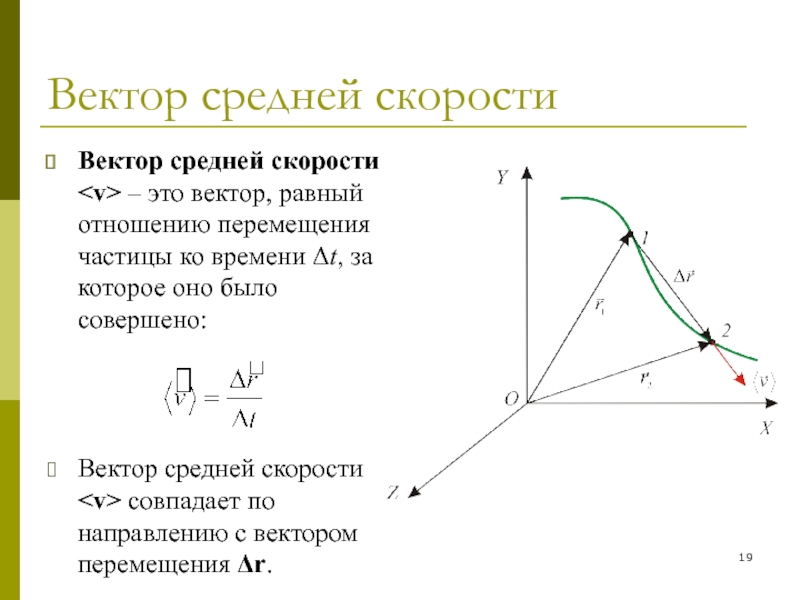
Вектор средней скорости – это вектор, равный
отношению перемещения частицы ко времени Δt, за которое оно было
совершено:
Вектор средней скорости
совпадает по направлению с вектором перемещения Δr.
Слайд 20Мгновенная скорость
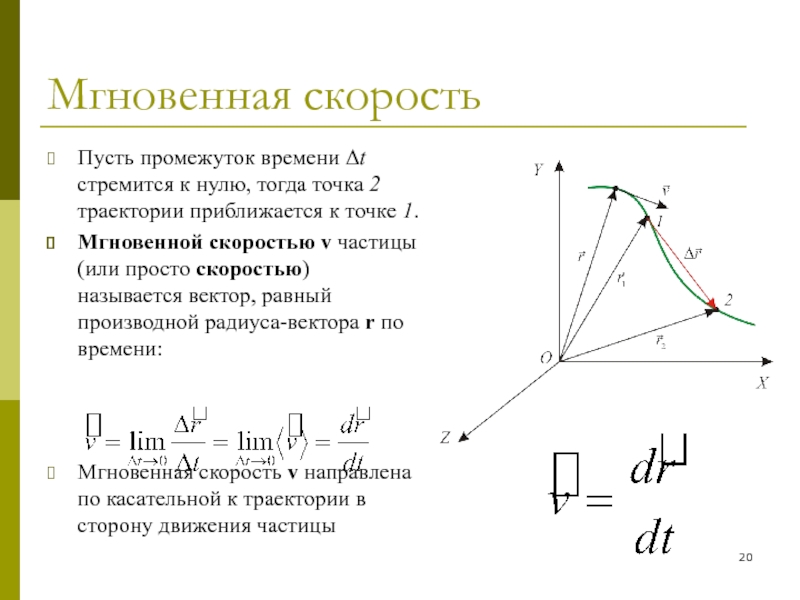
Пусть промежуток времени Δt стремится к нулю, тогда точка
2 траектории приближается к точке 1.
Мгновенной скоростью v частицы (или
просто скоростью) называется вектор, равный производной радиуса-вектора r по времени:
Мгновенная скорость v направлена по касательной к траектории в сторону движения частицы
Слайд 21Единица измерения скорости
В СИ скорость измеряется в метрах в секунду
(м/с).
1 км/ч = 1000 м/3600 с = 0,36 м/с
Слайд 22Ускорение
Ускорением называется вектор, равный производной по времени скорости v частицы:
Слайд 23Прямая и обратная задачи кинематики
Если зависимость радиуса-вектора от времени r(t)
известна, то можно решить т.н. прямую задачу кинематики – определить
скорость v и ускорение a частицы в любой момент времени t.
Обратная задача кинематики состоит в том, чтобы зная зависимость от времени ускорения a(t) и начальные условия движения (скорость v0 и радиус-вектор r0 в начальный момент времени t = 0), определить в любой момент времени скорость v и положение r частицы в пространстве.
Слайд 24ГЛАВА 1
ОСНОВЫ КИНЕМАТИКИ
1.3 Координатный способ описания движения материальной точки
Слайд 25Координатный способ задания движения
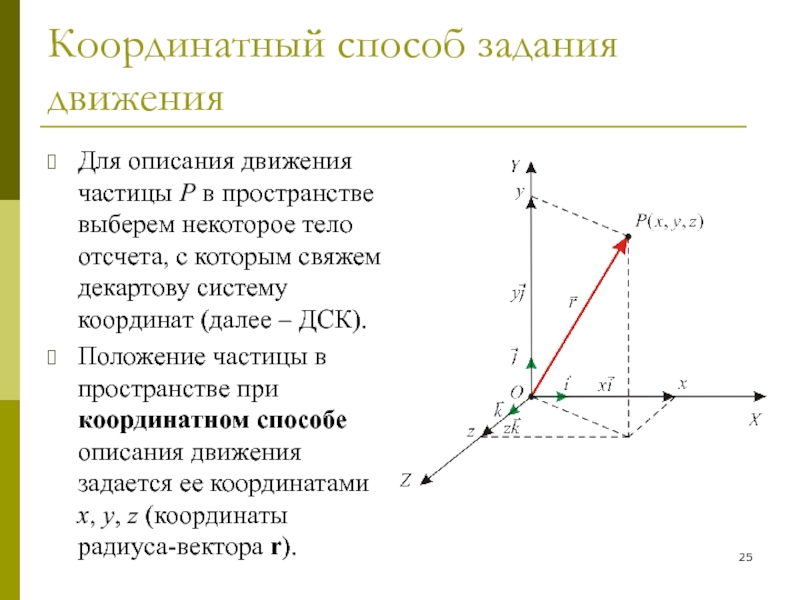
Для описания движения частицы P в пространстве
выберем некоторое тело отсчета, с которым свяжем декартову систему координат
(далее – ДСК).
Положение частицы в пространстве при координатном способе описания движения задается ее координатами x, y, z (координаты радиуса-вектора r).
Слайд 26Закон движения
Законом движения называется зависимость от времени координат частицы:
Между векторным
и координатным способами описания движения существует простая связь. Любой вектор
можно задать его проекциями на оси координат. Например, радиус-вектор частицы:
где i, j, k – орты координатных осей.
Слайд 27Скорость при координатном способе описания движения
Скорость v, как и любой
вектор, может быть представлена через проекции на оси ДСК:
Т.о., скорость
v частицы можно представить в следующем виде:
Видно, что компоненты скорости, выраженные через функции x(t), y(t), z(t), равны
Слайд 28Модуль и направление вектора скорости
Для каждого момента времени t можно
определить модуль и направление (с помощью направляющих косинусов) вектора скорости
v:
Здесь α, β, γ – углы, образованные вектором v с осями X, Y и Z соответственно
Слайд 29Ускорение при координатном способе задания движения
Ускорение a, как и любой
вектор, может быть представлен через проекции на оси ДСК:
Т.о., скорость
v частицы можно представить в следующем виде:
Видно, что компоненты скорости, выраженные через функции x(t), y(t), z(t), равны
Слайд 30Модуль и направление вектора ускорения
Для каждого момента времени t можно
определить модуль и направление (с помощью направляющих косинусов) вектора ускорения
a:
Здесь α′, β′, γ′ – углы, образованные вектором a с осями X, Y и Z соответственно
Слайд 31Путь
Пусть частица, двигаясь вдоль некоторой траектории, переместилась из точки 1
в точку 2.
Путь s (или Δs) равен измеренному вдоль траектории
расстоянию, пройденному частицей в процессе движения (длина траектории).
Путь является величиной скалярной, неотрицательной и неубывающей.
Слайд 32Связь между путем и модулем скорости частицы
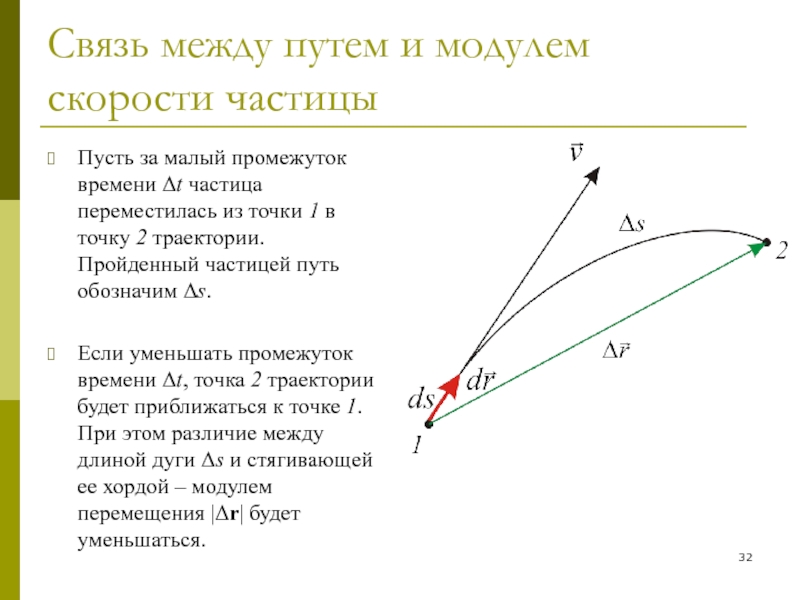
Пусть за малый промежуток
времени Δt частица переместилась из точки 1 в точку 2
траектории. Пройденный частицей путь обозначим Δs.
Если уменьшать промежуток времени Δt, точка 2 траектории будет приближаться к точке 1. При этом различие между длиной дуги Δs и стягивающей ее хордой – модулем перемещения |Δr| будет уменьшаться.
Слайд 33Связь между путем и модулем скорости частицы
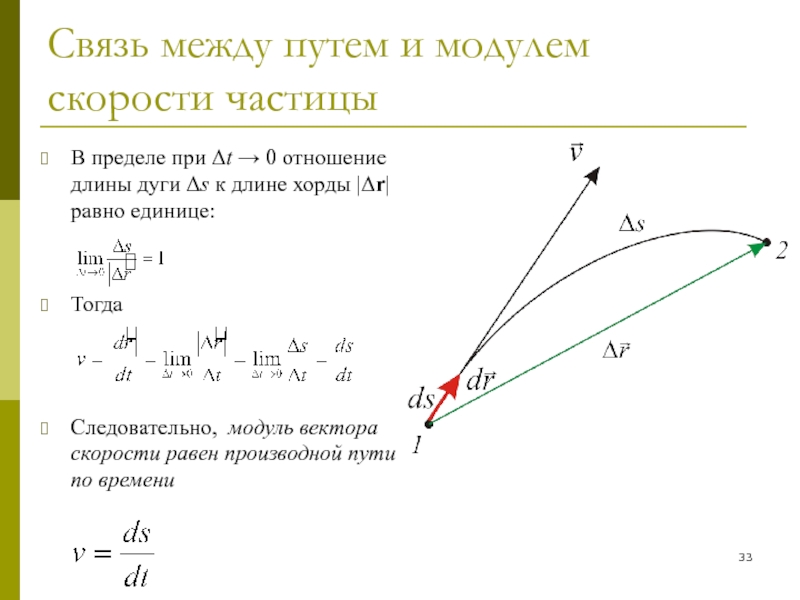
В пределе при Δt
→ 0 отношение длины дуги Δs к длине хорды |Δr|
равно единице:
Тогда
Следовательно, модуль вектора скорости равен производной пути по времени
Слайд 34Связь между путем и модулем скорости частицы
Зная зависимость модуля скорости
v от времени, можно вычислить пройденный частицей путь:
Интегрируя это равенство,
получим:
Слайд 35Графическое определение пути
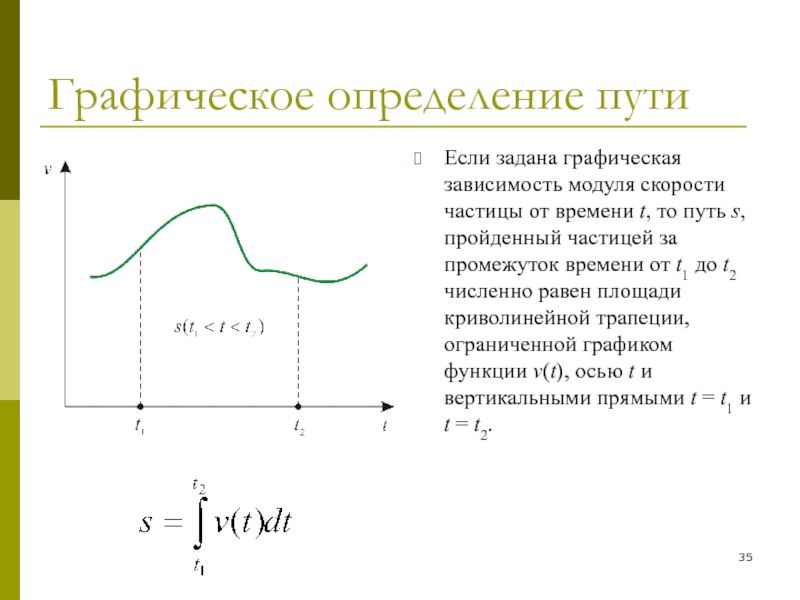
Если задана графическая зависимость модуля скорости частицы от
времени t, то путь s, пройденный частицей за промежуток времени
от t1 до t2 численно равен площади криволинейной трапеции, ограниченной графиком функции v(t), осью t и вертикальными прямыми t = t1 и t = t2.
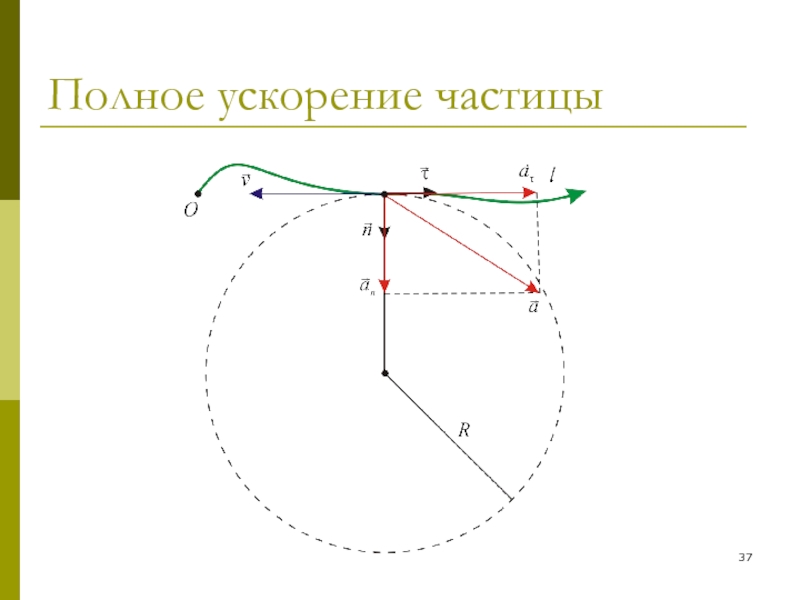
Слайд 36Полное ускорение частицы
Полное ускорение частицы a можно представить в виде
суммы двух перпендикулярных друг другу составляющих:
Модуль полного ускорения:
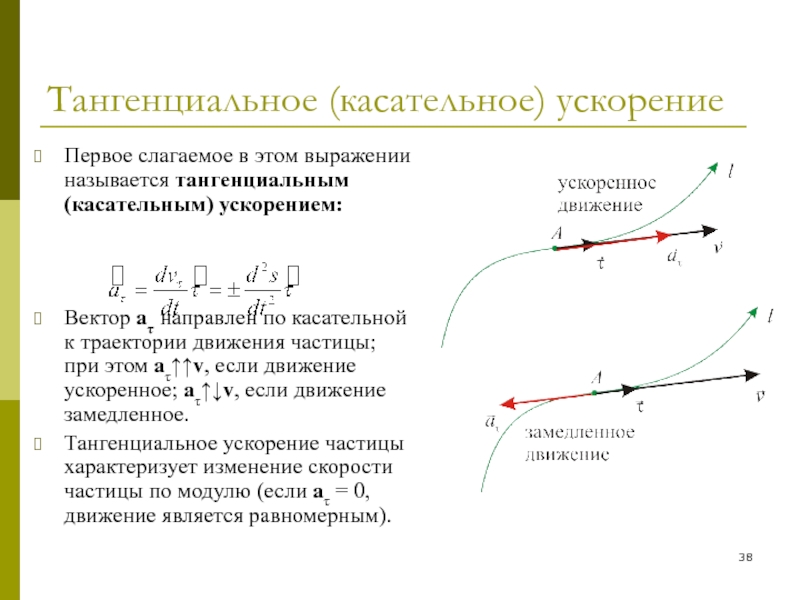
Слайд 38Тангенциальное (касательное) ускорение
Первое слагаемое в этом выражении называется тангенциальным (касательным)
ускорением:
Вектор aτ направлен по касательной к траектории движения частицы; при
этом aτ↑↑v, если движение ускоренное; aτ↑↓v, если движение замедленное.
Тангенциальное ускорение частицы характеризует изменение скорости частицы по модулю (если aτ = 0, движение является равномерным).
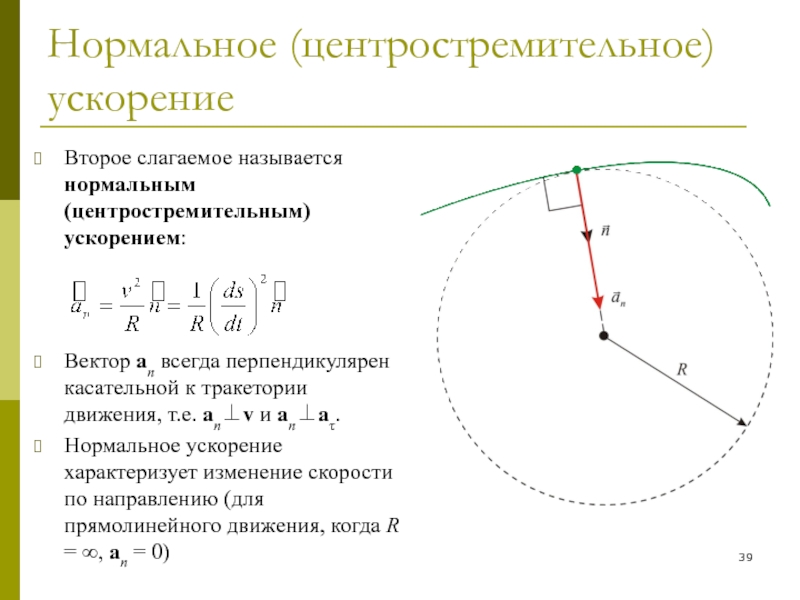
Слайд 39Нормальное (центростремительное) ускорение
Второе слагаемое называется нормальным (центростремительным) ускорением:
Вектор an всегда
перпендикулярен касательной к тракетории движения, т.е. an⊥v и an⊥aτ.
Нормальное ускорение
характеризует изменение скорости по направлению (для прямолинейного движения, когда R = ∞, an = 0)
Слайд 40ГЛАВА 1
ОСНОВЫ КИНЕМАТИКИ
1.4 Твердое тело в механике.
Виды движения
твердого тела
Слайд 41Абсолютно твердое тело
Абсолютно твердым телом в механике называют тело, при
движении которого расстояния между любыми двумя его точками остаются неизменными.
Таким
образом, твердое тело не деформируется под действием внешних сил.
Слайд 42Виды движения
абсолютно твердого тела
Различают 5 видов движения абсолютно твердого
тела:
поступательное движение;
вращение вокруг неподвижной оси;
плоское движение;
вращение вокруг неподвижной точки;
свободное движение
Первые
2 вида являются основными, остальные можно свести к одному из основных или к их совокупности.
Слайд 43Поступательное движение абсолютно твердого тела
При поступательном движении любая прямая, жестко
связанная с движущимся телом, остается параллельной своему начальному положению.
Слайд 44Вращение абсолютно твердого тела вокруг неподвижной оси
Вращением вокруг неподвижной оси
называется движение, при котором существуют по крайней мере 2 неподвижные
точки тела
Прямая, проходящая через эти точки, называется осью вращения
Все лежащие на оси точки неподвижны, а остальные точки тела вращаются по окружностям, перпендикулярным к оси вращения; скорости этих точек направлены по касательным к этим окружностям.
Слайд 45Плоское движение абсолютно твердого тела
При плоском движении траектория каждой точки
твердого тела расположена в некоторой фиксированной плоскости; плоскости движения всех
точек твердого тела параллельны между собой (т.е. все точки тела движутся в параллельных плоскостях).
Слайд 46Вращение абсолютно твердого тела
вокруг неподвижной точки
Вращение вокруг неподвижной точки
называется движение твердого тела, имеющего одну неподвижную точку (т.е. это
движение твердого тела, при котором существует только одна точка, скорость которой равна нулю)
Слайд 47Свободное движение абсолютно твердого тела
При свободном движении никаких кинематических ограничений
на движение твердого тела не накладывается.
Слайд 48Число степеней свободы
Число степеней свободы тела – это количество независимых
переменных (величин), которые необходимо задать, чтобы определить положение тела в
пространстве.
Пример. Число степеней свободы материальной точки равно 3 (три независимые переменные (координаты) x, y, z).
Слайд 49ГЛАВА 1
ОСНОВЫ КИНЕМАТИКИ
1.5 Вращение твердого тела
вокруг неподвижной оси
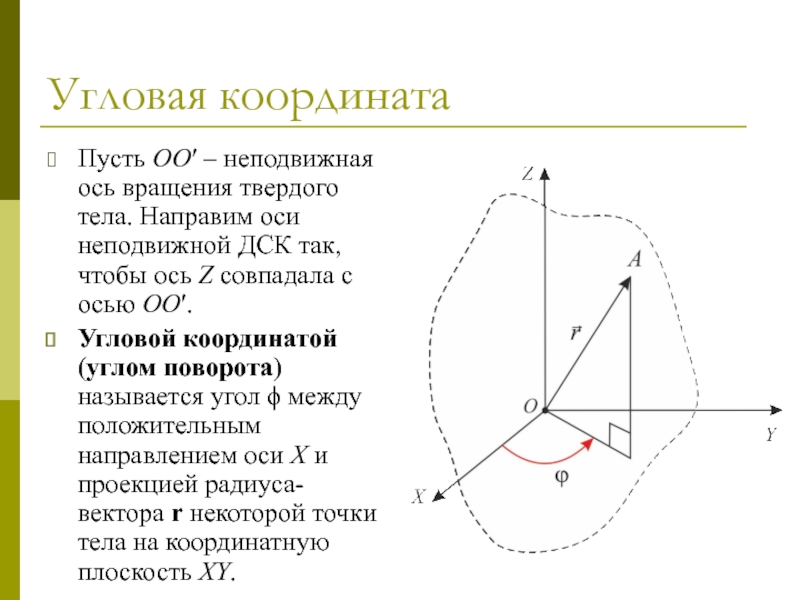
Слайд 50Угловая координата
Пусть OO′ – неподвижная ось вращения твердого тела. Направим
оси неподвижной ДСК так, чтобы ось Z совпадала с осью
OO′.
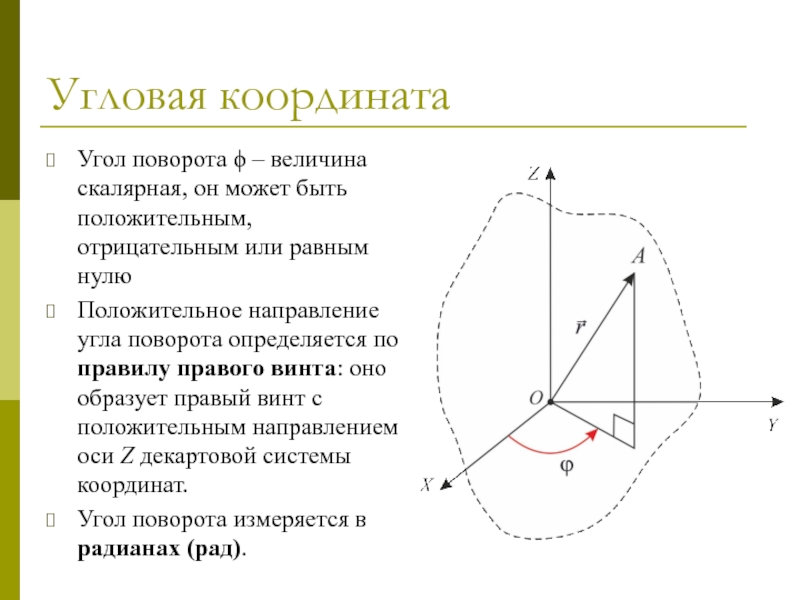
Угловой координатой (углом поворота) называется угол ϕ между положительным направлением оси X и проекцией радиуса-вектора r некоторой точки тела на координатную плоскость XY.
Слайд 51Угловая координата
Угол поворота ϕ – величина скалярная, он может быть
положительным, отрицательным или равным нулю
Положительное направление угла поворота определяется по
правилу правого винта: оно образует правый винт с положительным направлением оси Z декартовой системы координат.
Угол поворота измеряется в радианах (рад).
Слайд 52Вектор элементарного поворота
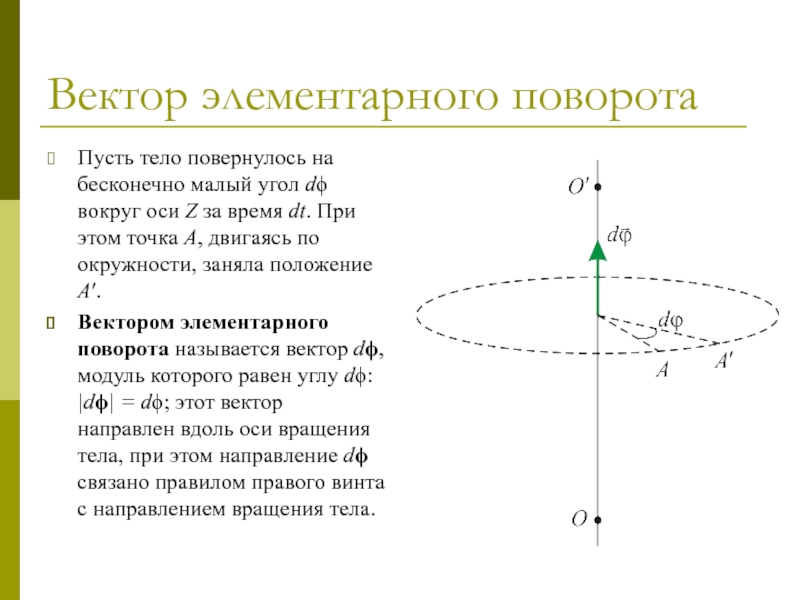
Пусть тело повернулось на бесконечно малый угол dϕ
вокруг оси Z за время dt. При этом точка A,
двигаясь по окружности, заняла положение A′.
Вектором элементарного поворота называется вектор dϕ, модуль которого равен углу dϕ: |dϕ| = dϕ; этот вектор направлен вдоль оси вращения тела, при этом направление dϕ связано правилом правого винта с направлением вращения тела.
Слайд 53Угловая скорость
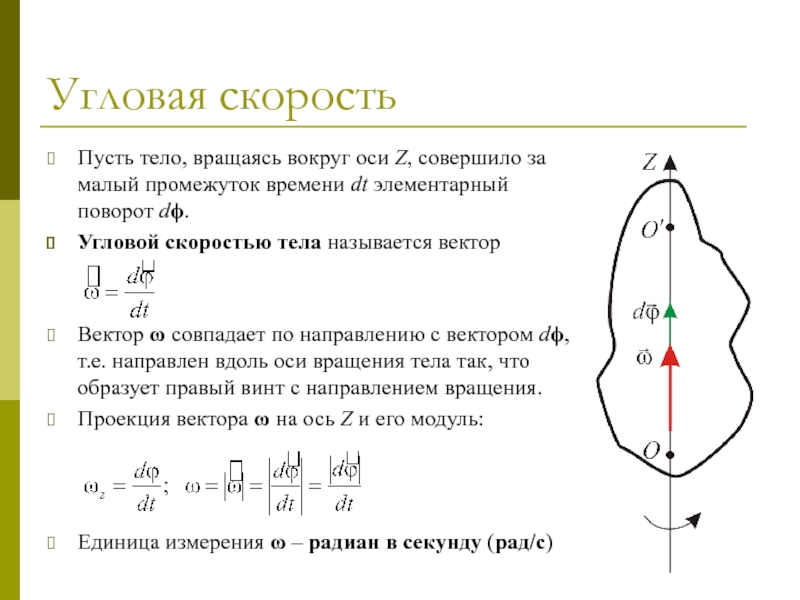
Пусть тело, вращаясь вокруг оси Z, совершило за малый
промежуток времени dt элементарный поворот dϕ.
Угловой скоростью тела называется вектор
Вектор
ω совпадает по направлению с вектором dϕ, т.е. направлен вдоль оси вращения тела так, что образует правый винт с направлением вращения.
Проекция вектора ω на ось Z и его модуль:
Единица измерения ω – радиан в секунду (рад/с)
Слайд 54Угловое ускорение
Угловым ускорением называется вектор, равный производной угловой скорости тела
по времени:
Проекция вектора углового ускорения ε на ось вращения Z:
Единица
углового ускорения в системе СИ – радиан на секунду в квадрате (рад/с2)
Слайд 55Угловое ускорение
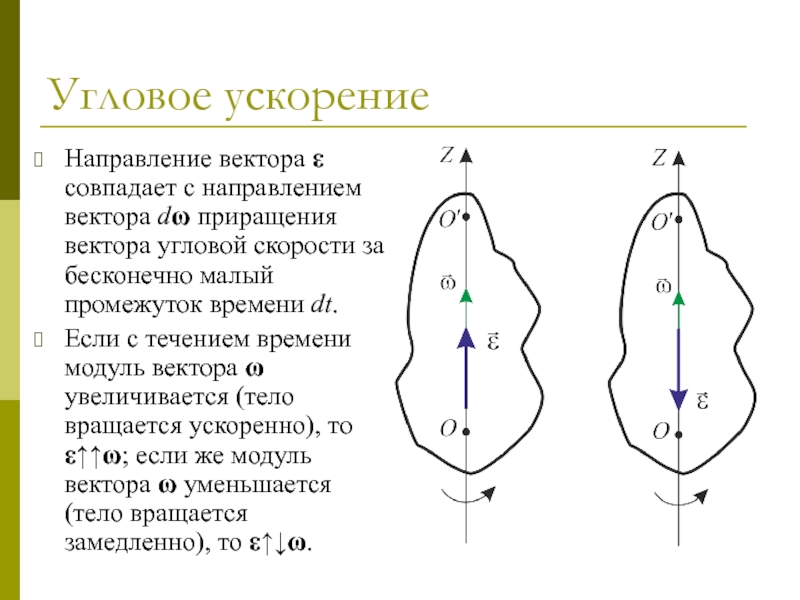
Направление вектора ε совпадает с направлением вектора dω приращения
вектора угловой скорости за бесконечно малый промежуток времени dt.
Если с
течением времени модуль вектора ω увеличивается (тело вращается ускоренно), то ε↑↑ω; если же модуль вектора ω уменьшается (тело вращается замедленно), то ε↑↓ω.
Слайд 56Связь между линейными и угловыми кинематическими величинами
Постановка задачи. Пусть твердое
тело вращается вокруг неподвижной оси Z с угловой скоростью ω
и угловым ускорением ε.
Найдем связь между линейными величинами – скоростью vA и ускорением aA произвольной точки A тела с угловыми величинами – угловой скоростью ω и угловым ускорением ε тела
Слайд 57Связь между линейными и угловыми кинематическими величинами
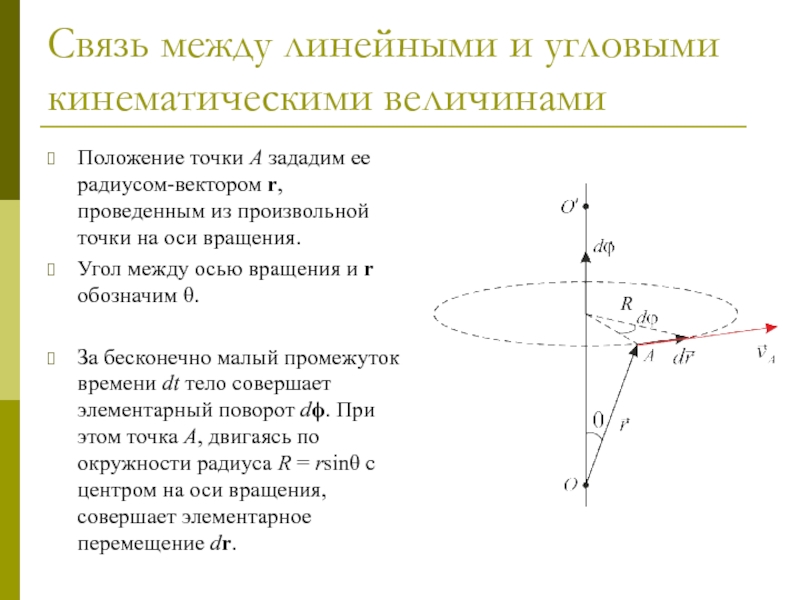
Положение точки A зададим
ее радиусом-вектором r, проведенным из произвольной точки на оси вращения.
Угол
между осью вращения и r обозначим θ.
За бесконечно малый промежуток времени dt тело совершает элементарный поворот dϕ. При этом точка A, двигаясь по окружности радиуса R = rsinθ с центром на оси вращения, совершает элементарное перемещение dr.
R
Слайд 58Линейная скорость точки АТТ
Модуль элементарного перемещения точки A:
или в векторной
форме:
Тогда скорость точки A:
Слайд 59Угловое ускорение точки АТТ
Найдем теперь выражение для ускорения точки A.
Согласно определению ускорения,
Первое слагаемое – это тангенциальное ускорение:
Второе слагаемое –
это нормальное ускорение:
Слайд 60Угловое ускорение точки АТТ
Таким образом, полное ускорение точки A твердого
тела:
Слайд 61ГЛАВА 1
ОСНОВЫ КИНЕМАТИКИ
1.6 Плоское движение твердого тела
Слайд 62Плоское движение твердого тела
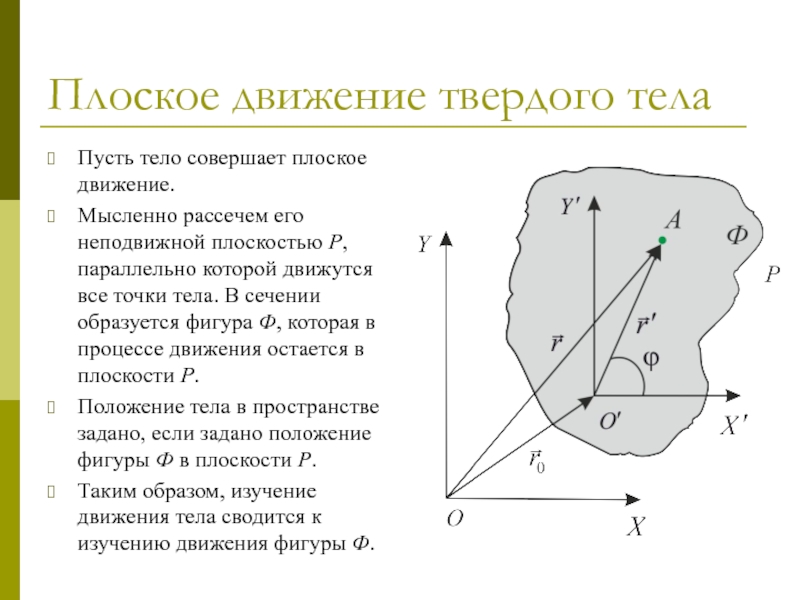
Пусть тело совершает плоское движение.
Мысленно рассечем его
неподвижной плоскостью P, параллельно которой движутся все точки тела. В
сечении образуется фигура Ф, которая в процессе движения остается в плоскости P.
Положение тела в пространстве задано, если задано положение фигуры Ф в плоскости P.
Таким образом, изучение движения тела сводится к изучению движения фигуры Ф.
Слайд 63Описание плоского движения твердого тела
Рассмотрим 2 системы отсчета: неподвижную OXY
и связанную с телом систему отсчета O′X′Y′.
Выберем произвольно точки O1
и A тела (точка O′ – начало подвижной координат).
Обозначим: r и r′ – радиус-вектора точки A тела относительно неподвижной и подвижной систем отсчета; r0 – радиус-вектор точки O′ относительно неподвижной системы отсчета. Тогда
Слайд 64Линейная скорость точки твердого тела при его плоском движении
Дифференцируем последнее
равенство по времени, получаем:
Здесь vA – скорость точки A тела
относительно неподвижной системы отсчета; v0 – скорость точки O′ тела в неподвижной системе отсчета; v′ – относительная скорость (скорость точки A относительно движущейся системы отсчета), обусловленная вращением тела вокруг проходящей через точку O′ перпендикулярной к плоскости движения неподвижной оси.
Слайд 65Мгновенная ось вращения
Таким образом, плоское движение твердого тела представляет собой
совокупность 2-х видов движения – поступательного вместе с произвольной точкой
O′ тела и вращения вокруг проходящей через эту точку неподвижной оси.
Если в некоторый момент времени скорость точки O′, относительно которой рассматривается вращение, равна нулю (v0 = 0), то проходящая через точку O′ ось, перпендикулярная к плоскости P, называется мгновенной осью вращения.
Слайд 66Вращение твердого тела вокруг неподвижной точки. Свободное движение
Вращение твердого тела
вокруг неподвижной точки в любой момент времени представляет собой вращение
вокруг мгновенной оси, проходящей через эту точку. С течением времени мгновенная ось, вообще говоря, непрерывно перемещается как в теле, так и в пространстве.
Свободное движение твердого тела можно рассматривать как совокупность двух движений – поступательного движения вместе с произвольной точкой тела и вращения вокруг проходящей через эту точку мгновенной оси, положение которой с течением времени непрерывно меняется как в теле, так и в пространстве.