Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Индуктивные умозаключения и их виды
Содержание
- 1. Индуктивные умозаключения и их виды
- 2. Вопросы1. Логическая природа индукции2. Научная индукция. Индуктивные методы установления причинных связей
- 3. Дедуктивные умозаключения позволяют выводить из истинных посылок
- 4. В определении индукции в логике выявляются два
- 5. «Что такое мужество?» — спросил когда-то у
- 6. Слайд 6
- 7. В то время как древние греки на
- 8. Напомнив об этом Лахесу, Сократ пояснил: «Я
- 9. В мужестве, утверждал Сократ, есть нечто общее,
- 10. На помощь растерявшемуся Лахесу Сократ призвал другого
- 11. Сократ удивился. Ведь подобный признак мужества можно
- 12. Сколько не бились ученики над загадкой
- 13. При втором подходе, присущем современной математической логике, индукцией называется умозаключение, дающее вероятностное суждение.
- 14. В зависимости от избранного основания выделяют индукцию полную и неполную. По другому основанию выделяют математическую индукцию.
- 15. Полной индукцией называется такое умозаключение, в котором
- 16. Земля вращается вокруг Солнца по эллиптической орбите.
- 17. Посылками в полной индукции могут быть и
- 18. Полная индукция дает достоверное заключение, поэтому она
- 19. По способам обоснования заключения неполная индукция делится
- 20. Слайд 20
- 21. Характерной и очень распространенной ошибкой является “поспешное
- 22. На основе популярной индукции народ вывел немало
- 23. Слайд 23
- 24. Слайд 24
- 25. 2. Индукция через анализ и отбор фактовВ
- 26. Так вычисляют среднюю урожайность поля, судят о
- 27. Изучая свойства серебра, люди обнаружили, что серебро
- 28. Позавчера двоечнику Н. перебежала дорогу черная кошка,
- 29. Дома вода кипит при температуре 100 градусов.На
- 30. Бэкон, Фрэнсис (Bacon, Francis) (1561–1626), барон Веруламский, виконт Сент-Олбанский, английский государственный деятель, эссеист и философ
- 31. Джон Стюарт Милль (1806-1873)
- 32. Метод единственного сходства
- 33. Суть метода единственного сходства заключается в следующем.
- 34. ПРИМЕР рассуждения на основе метода единственного сходства.
- 35. Слайд 35
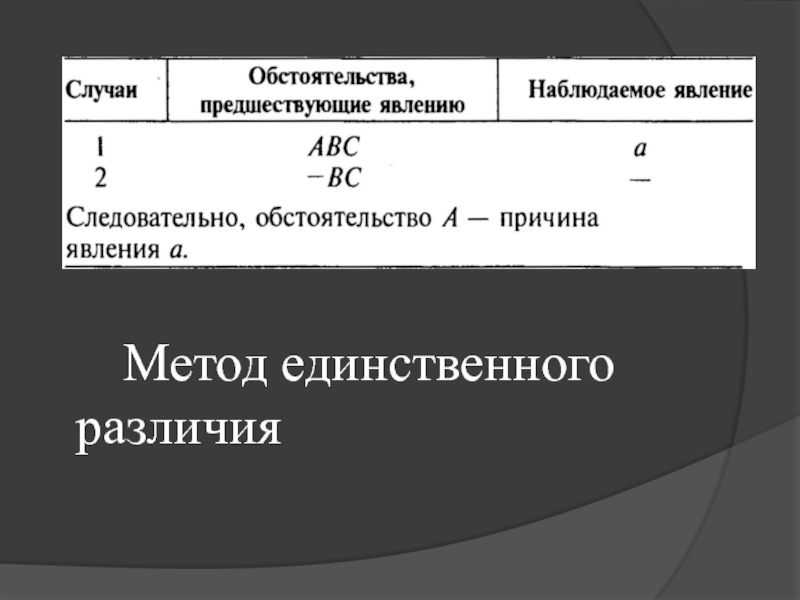
- 36. Метод единственного различия
- 37. Рассматриваются два случая. В первом обстоятельства ABC
- 38. ПРИМЕР: В прошлом веке считали, что животным
- 39. Н. И. Лунин
- 40. Слайд 40
- 41. Соединенный метод единства и различия
- 42. В первых случаях группы обстоятельств, сходные в
- 43. ПРИМЕР: Бобовые растения: горох, бобы, чечевица, соя
- 44. Слайд 44
- 45. Бугорки на корнях бобовых растений
- 46. Метод сопутствующих изменений
- 47. Этот метод заключается в следующем. Пусть обстоятельства
- 48. ПРИМЕР: Долгое время замечали, что высота морских
- 49. Слайд 49
- 50. Известно, например, что средний вес новорожденного ребенка
- 51. Слайд 51
- 52. Метод остатков. Суть этого метода заключается в
- 53. С помощью этого метода была открыта планета
- 54. Урбен Жан Жозеф Леверье (1811—1877)
- 55. Видимый облик планеты Нептун вы можете увидеть
- 56. Скачать презентанцию
Вопросы1. Логическая природа индукции2. Научная индукция. Индуктивные методы установления причинных связей
Слайды и текст этой презентации
Слайд 2Вопросы
1. Логическая природа индукции
2. Научная индукция. Индуктивные методы установления причинных
связей
Слайд 3Дедуктивные умозаключения позволяют выводить из истинных посылок при соблюдении соответствующих
правил истинные заключения.
Индуктивные умозаключения обычно дают нам не достоверные, а
лишь правдоподобные заключения.Слайд 4В определении индукции в логике выявляются два подхода.
Первый, осуществляемый в
традиционной (не в математической) логике, в которой индукцией называется умозаключение
от знания меньшей степени общности к новому знанию большей степени общности (т. е. от отдельных частных случаев мы переходим к общему суждению).Слайд 5 «Что такое мужество?» — спросил когда-то у своих учеников великий
греческий философ Сократ. Один из них, по имени Лахес, ответил,
почти не задумываясь, что мужествен в битве тот, «кто, оставаясь в строю на своем месте, старается отражать неприятелей и не бежит». Сократ согласился. Стойкость и смелость воинов действительно относятся к мужеству. Но это ведь еще не все мужество. Учитель ждал объяснения сути, а не примера мужественного поступка. Тем более, что и пример оказался не самым удачным.Слайд 7В то время как древние греки на войне предпочитали держаться
плотным строем, скифы, наоборот, атаковали, рассыпавшись по всему полю, и
дрались не менее смело, когда убегали. Так они заманивали противника в погоню за собой, чтобы затем одолеть, расстроив его ряды. Да и сами греки порой поступали так же.Спартанцы, например, в битве при Платее своим бегством вынудили персидских щитоносцев нарушить строй. Когда же те увлеклись преследованием бегущих, спартанцы внезапно повернули назад и победили неповоротливых персов в рукопашном бою. Подвижность и смекалка здесь пригодились грекам больше, чем стойкое, но неразумное сопротивление.
Слайд 8 Напомнив об этом Лахесу, Сократ пояснил: «Я хотел от тебя
узнать о мужественных не только в пехоте, но и в
коннице и вообще в военном деле, и не только на войне, а также во время опасностей на море, в болезнях, бедности или в государственных делах, и опять еще не о тех только, что мужественны относительно скорбей и страхов, но и кто силен в борьбе с вожделениями и удовольствиями».Слайд 9 В мужестве, утверждал Сократ, есть нечто общее, тождественное для любых
жизненных ситуаций. «Постарайся же и ты, Лахес, сказать... что это
за сила, которая, оставаясь одною и тою же при удовольствии и при огорчении, и при всех случаях... равно зовется мужеством?» В ответ ученик признался: «Понимать-то я, кажется, понимаю, что такое мужество, а вот только не знаю, как это оно сейчас от нас ушло, что я не успел схватить его и выразить словом».Слайд 10 На помощь растерявшемуся Лахесу Сократ призвал другого участника их беседы
— полководца Никия. Тот заявил, что мужество «есть некоторого рода
мудрость». Сократ опять не возражал, но потребовал объяснения: «Что это за наука или наука о чем?» Под наукой (или мудростью) Никий разумел «знание опасного и безопасного на войне и во всех других случаях».Слайд 11Сократ удивился. Ведь подобный признак мужества можно найти почти повсюду.
Врачи знают, что опасно в болезнях, земледельцы и ремесленники —
в своих делах. Каждый на своем месте знает, чего ему следует опасаться. Однако от этого знания никто не становится более мужественным. Да и вообще, не всякое знание добродетельно. Мудрость дает нам силу духа. Здесь Никий был прав.Но мудрость содержится отнюдь не во всех науках, а лишь в тех, что приносят благо. То же стоит сказать и о мужестве. Сообразительность не делает героями подлецов, а безрассудный азарт или дурное упорство никому не приносят пользы.
Слайд 12 Сколько не бились ученики над загадкой Сократа, разрешить ее до
конца они так и не смогли. В итоге учитель заключил,
что спорившие не достигли поставленной цели. «Все мы, — сказал он, — одинаково оказываемся в затруднении». Так заканчивается знаменитый философский диалог о мужестве «Лахес», дошедший до нас из глубины веков в изложении Платона (преемника Сократа), основателя первой в мире научной академии.Слайд 13При втором подходе, присущем современной математической логике, индукцией называется умозаключение,
дающее вероятностное суждение.
Слайд 14В зависимости от избранного основания выделяют индукцию полную и неполную.
По другому основанию выделяют математическую индукцию.
Слайд 15Полной индукцией называется такое умозаключение, в котором общее заключение о
всех элементах класса предметов делается на основании рассмотрения каждого элемента
этого класса. В полной индукции изучаются все предметы данного класса, а посылками служат единичные суждения. Например:Слайд 16Земля вращается вокруг Солнца по эллиптической орбите.
Марс вращается вокруг
Солнца по эллиптической орбите.
Юпитер вращается вокруг Солнца по эллиптической
орбите. Сатурн вращается вокруг Солнца по эллиптической орбите.
Плутон вращается вокруг Солнца по эллиптической орбите.
Венера вращается вокруг Солнца по эллиптической орбите.
Уран вращается вокруг Солнца по эллиптической орбите.
Нептун вращается вокруг Солнца по эллиптической орбите.
Меркурий вращается вокруг Солнца по эллиптической орбите.
Земля, Марс, Юпитер, Сатурн, Плутон, Венера, Уран, Нептун, Меркурий -планеты Солнечной системы.
Все планеты Солнечной системы вращаются вокруг Солнца по эллиптической орбите.
Слайд 17Посылками в полной индукции могут быть и общие суждения. Например:
Все
моржи - водные млекопитающие.
Все ушастые тюлени - водные млекопитающие.
Все настоящие тюлени - водные млекопитающие.
Моржи, ушастые тюлени, настоящие тюлени представляют семейство ластоногих.
Все ластоногие - водные млекопитающие.
Слайд 18Полная индукция дает достоверное заключение, поэтому она часто применяется в
математических и в других самых строгих доказательствах. Чтобы использовать полную
индукцию, надо выполнить следующие условия:1. Точно знать число предметов или явлений, подлежащих рассмотрению.
2. Убедиться, что признак принадлежит каждому элементу этого класса.
3. Число элементов изучаемого класса должно быть невелико.
Слайд 19По способам обоснования заключения неполная индукция делится на следующие три
вида.
/. Индукция через простое перечисление (популярная)
На основании повторяемости одного и
того же признака у ряда однородных предметов и отсутствия противоречащего случая делается общее заключение, что все предметы этого рода обладают этим признаком. Например, на основе этой индукции раньше считали, что все лебеди белые - до тех пор пока не встретили в Австралии черных лебедей. Эта индукция дает заключение вероятностное, но не достоверное.Слайд 21Характерной и очень распространенной ошибкой является “поспешное обобщение”. Например, когда,
столкнувшись несколько раз с ошибками в свидетельских показаниях, говорят: “Все
свидетели ошибаются”, или ученику заявляют: “Ты ничего не знаешь по данному вопросу” и т. п.Слайд 22На основе популярной индукции народ вывел немало полезных примет: ласточки
низко летают - быть дождю; если закат солнца красный, то
завтра будет ветреный день, и др.Слайд 252. Индукция через анализ и отбор фактов
В популярной индукции наблюдаемые
объемы выбираются случайно, без всякой системы. В индукции через анализ
и отбор фактов стремятся исключить случайность обобщений, так как изучаются планомерно отобранные, наиболее типичные предметы - разнообразные по времени, способу получения и существования и другим условиям.Слайд 26Так вычисляют среднюю урожайность поля, судят о всхожести семян, о
качестве больших партий товаров, составе найденных полезных ископаемых. Например, при
изучении качества рыбных консервов банки берутся из разных холодильников, выпущенные в разные сроки, различными заводами, из различных сортов рыбы.Слайд 27Изучая свойства серебра, люди обнаружили, что серебро активирует кислород, уничтожающий
бактерии. С помощью серебра очищают питьевую воду. Хирурги применяют серебросодержащие
кремы при лечении ожогов и скрепляют кости цементом, который содержит бактерицидные соли серебра. Многим тысячам людей, пострадавшим от тяжелых ожогов, жизнь спасли, применив препараты, включающие серебро. Так, на основе индукции через отбор, планомерно изучая свойства серебра, люди сделали правильные заключения от возможности и необходимости применения серебра при лечении различных заболеваний.Слайд 28Позавчера двоечнику Н. перебежала дорогу черная кошка, и он получил
двойку.
Вчера двоечнику Н. перебежала дорогу черная кошка, и его родителей
вызвали в школу.Сегодня двоечнику Н. перебежала дорогу черная кошка, и его исключили из школы
_______________________________________
Во всех несчастьях двоечника Н. виновата черная кошка
Слайд 29Дома вода кипит при температуре 100 градусов.
На улице вода кипит
при температуре 100 градусов.
В лаборатории вода кипит при температуре 100
градусов.___________________________
Вода везде кипит при температуре 100 градусов.
Слайд 30Бэкон, Фрэнсис (Bacon, Francis) (1561–1626), барон Веруламский, виконт Сент-Олбанский, английский
государственный деятель, эссеист и философ
Слайд 33Суть метода единственного сходства заключается в следующем. Рассматриваются различные случаи,
когда наблюдается явление а. Во всех случаях явлению а предшествуют
группы обстоятельств, сходные только в отношении обстоятельства А. Отсюда делается вывод о том, что обстоятельство А является причиной (в указанном выше смысле) явления а.Слайд 34ПРИМЕР рассуждения на основе метода единственного сходства. Английский физик Д.
Брюстер следующим образом открыл причину переливов радужных цветов на поверхности
перламутровых раковин. Случайно он получил отпечаток перламутровой раковины на воске и обнаружил на поверхности воска ту же игру радужных цветов, что и на раковине. Он сделал отпечатки раковины на гипсе, смоле, каучуке и других веществах и убедился, что не особый химический состав вещества перламутровой раковины, а определенное химическое строение ее внутренней поверхности вызывает эту прекрасную игру цветов.Слайд 37Рассматриваются два случая. В первом обстоятельства ABC предшествуют явлению а;
во втором одно из обстоятельств (А) отсутствует, явление а тоже
отсутствует. Делается вывод о том, что отсутствующее обстоятельство является причиной явления а.Слайд 38ПРИМЕР: В прошлом веке считали, что животным для поддержания жизни
необходимо потреблять лишь белки и соли. Это мнение опроверг в
1880 г. русский доктор Н.И. Лунин. Он проделал следующий опыт. Одну группу мышей кормил обычной пищей, а другую — очищенными белками (обстоятельство В) и солями (обстоятельство С). Мыши второй группы через некоторое время погибли (второй случай по схеме). Лунин сделал вывод о том, что животным кроме белков и солей нужно что-то еще. Затем этот недостающий компонент питания был открыт. Им оказались витамины.Слайд 42В первых случаях группы обстоятельств, сходные в отношении одного обстоятельства,
предшествуют явлению а. В последних случаях в группах обстоятельств отсутствует
А, остальные обстоятельства имеют место, а явление а отсутствует.Слайд 43ПРИМЕР: Бобовые растения: горох, бобы, чечевица, соя и т.д. —
не только не нуждаются в азотных удобрениях, но и сами
обогащают землю азотом. Другие, небобовые растения нуждаются в азотном удобрении. В чем причина того, что бобовые растения не нуждаются в азотных удобрениях и даже обогащают землю азотом? Наблюдали различные бобовые растения. Оказалось, что все они имеют на корнях белые бугорки, т.е. все они сходны в одном обстоятельстве А. Небобовые растения не имеют на корнях белых бугорков, т.е. при сходстве других обстоятельств обстоятельство А у них отсутствует. Сделали заключение о том, что белые бугорки на корнях бобовых растений являются причиной обогащения почвы азотом. Затем было установлено, что в этих бугорках живут бактерии, которые обогащают почву азотом.Слайд 47Этот метод заключается в следующем. Пусть обстоятельства ABC предшествуют явлению
а. Если изменение одного из предшествующих обстоятельств (А) (при неизменности
остальных) вызывает изменение явления а, то изменение обстоятельства А является причиной изменения явления а. (В некоторых случаях посредством этого метода выясняется, что изменяющееся обстоятельство А Является причиной изменяющегося явления а.)Слайд 48ПРИМЕР: Долгое время замечали, что высота морских приливов и их
периодичность связаны с изменениями положения Луны. Наибольшие приливы бывают в
дни полнолуний и новолуний, наименьшие — в дни, когда линии, мысленно проведенные от Земли к Луне, а от Луны к Солнцу, образуют прямой угол. Сделали заключение о том, что изменение положения Луны вызывает изменение морских приливов и отливов.Методом сопутствующих изменений пользуются в тех случаях, когда предшествующие явлению обстоятельства нельзя
изолировать друг от друга, т.е. когда нельзя применить метод единственного различия.