Слайд 1ИНФОРМАТИКА
ОСНОВЫ
МАТЕМАТИЧЕСКОЙ
ЛОГИКИ
Лепустин А.В.
Ст. преп. ОИТ ОШИТР
Слайд 2Лекция 1
История математической логики
Высказывания
Таблицы истинности (ТИ)
Построение ТИ по формуле
Слайд 3История алгебры логики
Логика – наука, изучающая методы доказательств и опровержений.
Математическая логика – это современная форма логики, которая полностью опирается
на формальные математические методы.
С помощью алгебры логики пытаются решать традиционные логические задачи алгебраическими методами.
Слайд 5ВЫСКАЗЫВАНИЯ
Алгебра логики – это раздел математики, изучающий высказывания и логических
операций над ними.
Высказывания рассматриваются только с точки зрения их логических
значений (истинности или ложности)
смысл высказываний не рассматривается
Слайд 6ВЫСКАЗЫВАНИЯ
Объектами логики являются логические высказывания, принимающие значения логических величин.
Логические величины
– понятия, выражаемые словами ИСТИНА, ЛОЖЬ.
Слайд 7ВЫСКАЗЫВАНИЯ
Положительная логика:
ИСТИНА = 1 ЛОЖЬ = 0
Отрицательная логика:
ИСТИНА = 0 ЛОЖЬ =
Слайд 8ВЫСКАЗЫВАНИЯ
Высказыванием называется утвердительное повествовательное предложение, про которое есть смысл говорить,
истинно оно или ложно.
Слайд 9ИСТИНО
ВЫСКАЗЫВАНИЯ
Высказыванием называется утвердительное повествовательное предложение, про которое есть смысл говорить,
истинно оно или ложно.
Пример:
«9 делится на 3 без
остатка»;
«5>2»;
«Рим – столица Франции»;
«Для всякого целого n>2 уравнение xn+yn=zn не
имеет решения в натуральных числах».
ИСТИНО
ИСТИНО
ЛОЖНО
?
Теорема сформулирована в 1637, доказана в 1995
Слайд 10ВЫСКАЗЫВАНИЯ
Высказывания обычно обозначаются буквами
латинского алфавита: A, B, C, …, X,
Y, Z
Высказываниями не являются:
вопросительные и восклицательные предложения;
предложения, в которых
выражается призыв произвести какие-либо действия;
отвлеченные предложения и т. д.
Пример:
«Давай пойдём обедать»;
«2+3».
Слайд 11ВЫСКАЗЫВАНИЯ
Высказывательная форма – это повествовательное предложение, которое прямо или косвенно
содержит хотя бы одну переменную и становится высказыванием, когда все
переменные замещаются своими значениями.
Пример:
«В городе A более миллиона жителей»;
«У него голубые глаза».
Слайд 12ВЫСКАЗЫВАНИЯ
Алгебра логики рассматривает любое высказывание только с одной точки зрения
– является ли оно истинным или ложным.
Слайд 13ВЫСКАЗЫВАНИЯ
Является ли высказыванием?
СОЛНЦЕ ЯВЛЯЕТСЯ ЗВЕЗДОЙ
Слайд 14ВЫСКАЗЫВАНИЯ
Является ли высказыванием?
ЗЕМЛЯ ВРАЩАЕТСЯ ВОКРУГ СОЛНЦА
Слайд 15ВЫСКАЗЫВАНИЯ
Является ли высказыванием?
СОЛНЦЕ ВРАЩАЕТСЯ ВОКРУГ ЗЕМЛИ
Слайд 16ВЫСКАЗЫВАНИЯ
Является ли высказыванием?
СЕЙЧАС ДЕНЬ
Слайд 17ВЫСКАЗЫВАНИЯ
Является ли высказыванием?
В ДАННЫЙ МОМЕНТ МЫ НАХОДИМСЯ НА УРОКЕ
Слайд 18ВЫСКАЗЫВАНИЯ
Является ли высказыванием?
ЗАВТРА Я ПОЙДУ В ШКОЛУ
Слайд 19ВЫСКАЗЫВАНИЯ
Является ли высказыванием?
Площадь поверхности Индийского океана равна 75 млн. км2
Слайд 21ТАБЛИЦЫ ИСТИННОСТИ
Таблица истинности для функции n переменных – таблица, состоящая
из n+1 столбцов и 2n строк, в которой:
в n
столбцах слева перебираются все наборы значений переменных-аргументов,
в правом столбце записываются значения функции, вычисленные по каждой комбинации значений.
Слайд 23ТАБЛИЦЫ ИСТИННОСТИ
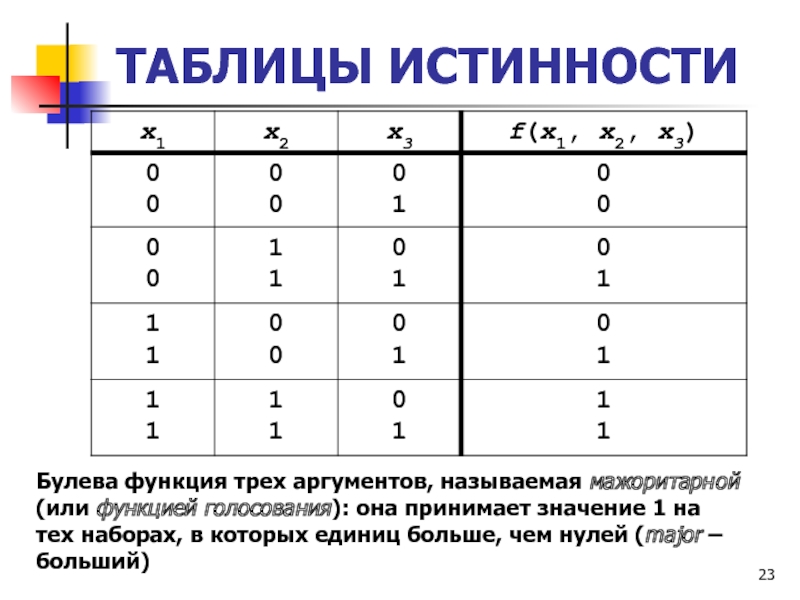
Булева функция трех аргументов, называемая мажоритарной (или функцией голосования):
она принимает значение 1 на тех наборах, в которых единиц
больше, чем нулей (major – больший)
Слайд 24ТАБЛИЦЫ ИСТИННОСТИ
Левая часть ТИ постоянна для всех функций с одинаковым
числом аргументов. Поэтому, задавая несколько таких функций, можно не повторять
левую часть таблицы, а в ее правой части перечислить столбцы значений всех функций
Слайд 25ТАБЛИЦЫ ИСТИННОСТИ
Булевы функции f1(x1, x2), f2(x1, x2), f3(x1, x2) могут
быть заданы общей таблицей:
Слайд 26ТАБЛИЦЫ ИСТИННОСТИ
Теорема о числе булевых функций
Число различных булевых функций, зависящих
от n переменных, равно
Слайд 28ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Все примеры высказываний, приведенные ранее, представляют собой высказывания, утверждающие
какой-либо один факт, то есть являются простыми
Простое высказывание – это
высказывание, в котором нельзя выделить часть, которая, в свою очередь, является высказыванием
Слайд 29ЛОГИЧЕСКИЕ ОПЕРАЦИИ
В логике, как и в любом литературном языке, из
простых высказываний можно создавать составные, используя логические связки
Литературный вариант:
Мальчики
Петров и Сидоров являются шахматистами
Логический вариант:
(Петров – шахматист) И (Сидоров – шахматист)
Два простых высказывания:
А=«Петров – шахматист»
В=«Сидоров – шахматист»
Логическая связка И
Слайд 30ЛОГИЧЕСКИЕ ОПЕРАЦИИ
В логике, как и в любом литературном языке, из
простых высказываний можно создавать составные, используя логические связки
Мы хотим отрицать
утверждение
Х=«Земля – безжизненная планета»
А=«Земля – не безжизненная планета»
В=«не(Земля – безжизненная планета)»
А – простое? составное?
В – простое? составное?
Слайд 31ЛОГИЧЕСКИЕ ОПЕРАЦИИ
С литературной точки зрения предпочтительнее, естественно, высказывание А
С точки
же зрения логики разницы в использовании выражений нет, можно сказать,
что высказывание A равно высказыванию B (если нет привязки к X; в противном случае А – переменная, В – функция)
Слайд 32ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Попытка предположить события, которые произойдут (или не произойдут) в
будущем и описать нашу реакцию на них:
«Если завтра пойдет снег,
то мы поиграем в снежки на перемене»
Два простых высказывания:
А=«завтра пойдет снег»
В=«мы поиграем в снежки на перемене»
Логическая связка «если…то…»
Слайд 33ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Рассмотренные логические связки, в основном, используются для словесной интерпретации
логического выражения
Связки, используемые в формальном выражении, получили название логические операции
(или элементарные булевы функции)
Слайд 34ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Вопросы на понимание:
Что такое
«формальное выражение»?
Что такое
«функция»?
Слайд 35ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Для удобства задания функции формальным образом будем пользоваться таблицами
истинности
Если значение функция зависит от значения некой переменной, то говорят,
что эта переменная является аргументом функции
Рассмотрим все элементарные булевы функции двух и менее аргументов
(n – количество аргументов)
Слайд 36ЛОГИЧЕСКИЕ ОПЕРАЦИИ
При n=0 имеем две функции:
Константа 0
Константа 1
Слайд 37ЛОГИЧЕСКИЕ ОПЕРАЦИИ
При n=1 имеем четыре функции:
Функции f0 и f3 не
зависят от x, уже были рассмотрены
– тождественная функция (читается «х»)
– функция отрицания (читается «не х»)
Слайд 38ОТРИЦАНИЕ
Операция f2 выражается связкой НЕ
Названия:
инверсия (лат. inversum – наоборот)
отрицание
Обозначения:
Единственная
унарная операция
Слайд 39ЛОГИЧЕСКИЕ ОПЕРАЦИИ
При n=2 имеем 16 функций:
Функции f0, f3, f5, f10,
f12, f15 не зависят хотя бы от одной из переменных
x1 и x2, и поэтому уже были рассмотрены ранее. Остальные 10 функций являются операциями над двумя переменными, они называются бинарными операциями.
Слайд 40КОНЪЮНКЦИЯ
Операция f1 выражается связкой И
Названия:
конъюнкция (лат. conjunctio – соединение)
логическое
умножение
Обозначения:
Слайд 41КОНЪЮНКЦИЯ
Для запоминания:
истинность операции требует истинности обоих аргументов одновременно
Слайд 42ДИЗЪЮНКЦИЯ
Операция f7 выражается связкой ИЛИ
(в неразделительном смысле этого слова)
Названия:
дизъюнкция (лат. disjunctio – разделение)
логическое сложение
Обозначения:
Слайд 43ДИЗЪЮНКЦИЯ
Для запоминания:
истинность операции требует истинности хотя бы одного из
аргументов
Слайд 44ИСКЛЮЧАЮЩЕЕ ИЛИ
Операция f6 выражается связкой ИЛИ
(в разделительном смысле этого
слова)
Названия:
исключающее ИЛИ
сумма по модулю 2
Обозначение:
Слайд 45ИСКЛЮЧАЮЩЕЕ ИЛИ
Для запоминания:
истинность операции требует, чтобы
значения аргументов были различны
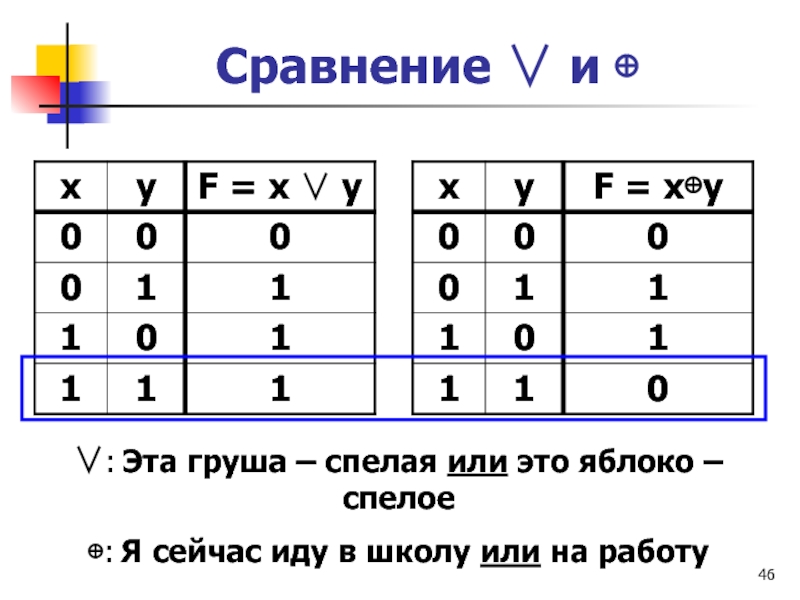
Слайд 46Сравнение и
: Эта груша – спелая или это
яблоко – спелое
: Я сейчас иду в школу или на
работу
Слайд 47ИМПЛИКАЦИЯ
Операция f13 выражается связками:
«если…, то…»
«из…следует…»
«…влечет…»
Названия:
импликация
логическое следование
Обозначение:
Слайд 48ИМПЛИКАЦИЯ
Для запоминания:
истинность операции требует, чтобы
выполнялось математическое
Слайд 49ЭКВИВАЛЕНТНОСТЬ
Операция f9 выражается связками:
«тогда и только тогда, когда»
«необходимо и достаточно»
«…равносильно…»
«…такой же, как…»
Названия:
эквивалентность
двойная импликация
Обозначения:
Слайд 50ЭКВИВАЛЕНТНОСТЬ
Для запоминания:
истинность операции требует, чтобы
значения аргументов были одинаковыми
Слайд 51ДРУГИЕ ОПЕРАЦИИ
Обратная импликация f11
Стрелка Пирса f8
Штрих Шеффера f14
Коимпликация f2
Обратная коимпликация
Слайд 52ОБОЗНАЧЕНИЯ
В дальнейшем будем считать основными обозначениями операций следующие:
конъюнкция:
дизъюнкция:
эквивалентность:
Слайд 53ВАЖНО !!!
Высказывания А и В, образующие любые составные высказывания А?В,
могут быть совершенно не связаны по содержанию, например:
А=«три меньше
двух»
В=«пингвины живут в Антарктиде»
Слайд 54ВАЖНО !!!
Алгебра логики рассматривает любое высказывание только с одной точки
зрения:
является ли оно
истинным или ложным.
Слайд 56ПРИОРИТЕТ ОПЕРАЦИЙ
Приоритеты операций в порядке убывания:
Унарное отрицание (НЕ).
Конъюнкция (И).
Все
остальные бинарные операции.
Слайд 57ПРИОРИТЕТ ОПЕРАЦИЙ
Необходимо иметь в виду:
операция НЕ имеет высший приоритет
при вычислениях инверсии переменных, например:
в случае вычисления инверсии выражения вначале
вычисляется значение выражения, а затем оно инвертируется:
Слайд 58ПРИОРИТЕТ ОПЕРАЦИЙ
В остальных случаях пользуются следующими правилами:
скобки изменяют порядок выполнения
действий (но не приоритет операций!) в конкретном выражении
если в формуле
подряд следуют несколько операций одинакового приоритета, то они выполняются слева направо.
Слайд 59ПРИОРИТЕТ ОПЕРАЦИЙ
Аналогия из математики: 4/5*2 :
(4/5)*2 = 1.6 4/(5*2) = 0.4
В
логике:
Слайд 61ВИДЫ ЛОГИЧЕСКИХ ФОРМУЛ
Все логические формулы можно разделить на три группы:
Выполнимые
формулы
Тождественно истинные формулы (тавтологии)
Тождественно ложные формулы (противоречия)
Слайд 62ВИДЫ ЛОГИЧЕСКИХ ФОРМУЛ
Все пары логических формул, зависящих от одного и
того же набора переменных-параметров, можно разделить на три группы:
Равносильные
(тождественные) формулы
Совместимые формулы
Противоположные (инверсные) формулы
Слайд 63ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ПО ФОРМУЛЕ
Слайд 64ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
Задание:
Построить таблицу истинности по формуле
Слайд 65ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
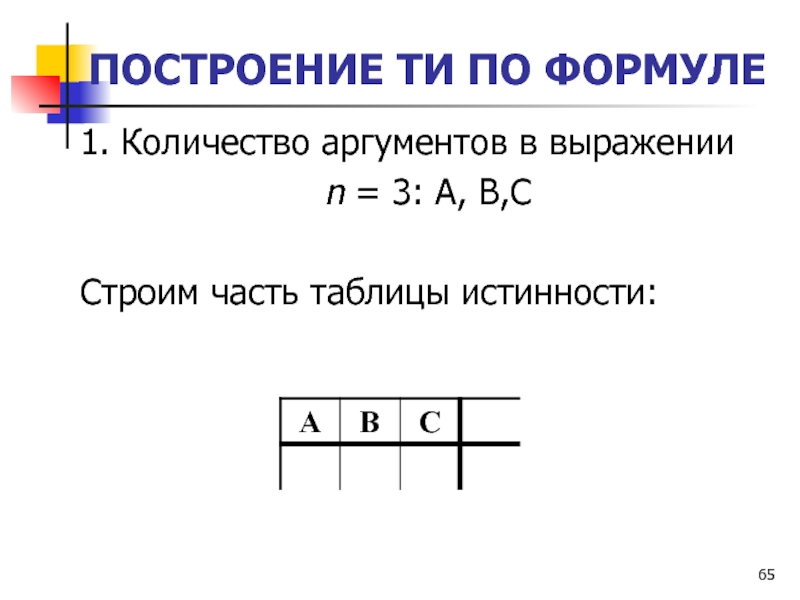
1. Количество аргументов в выражении
n = 3:
A, B,C
Строим часть таблицы истинности:
Слайд 66ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
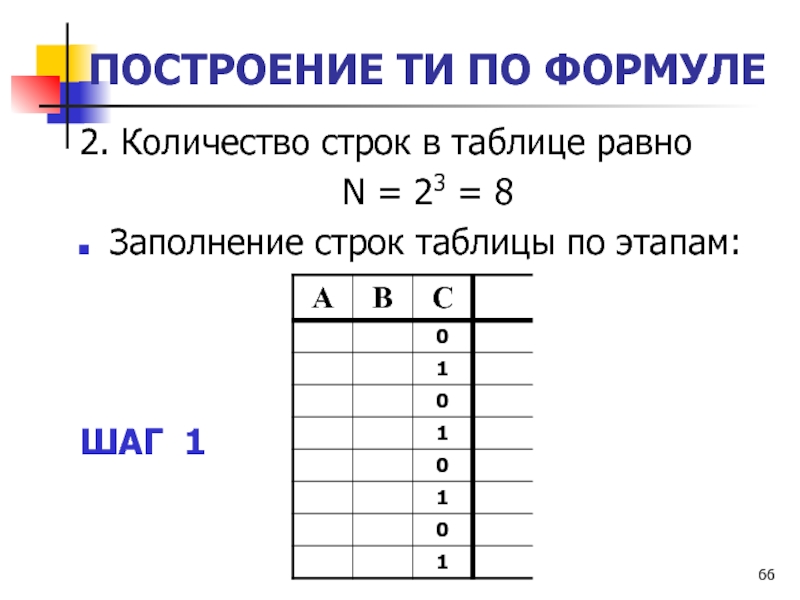
2. Количество строк в таблице равно
N =
23 = 8
Заполнение строк таблицы по этапам:
ШАГ 1
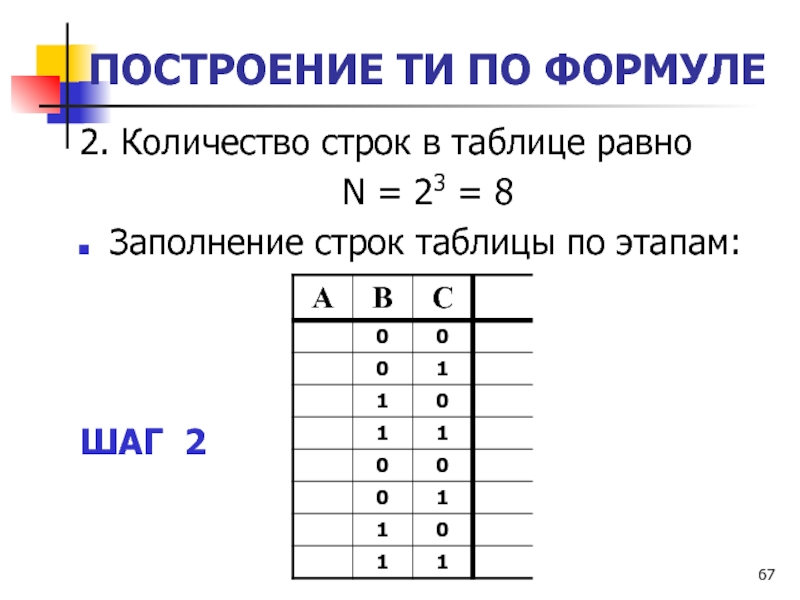
Слайд 67ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
2. Количество строк в таблице равно
N =
23 = 8
Заполнение строк таблицы по этапам:
ШАГ 2
Слайд 68ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
2. Количество строк в таблице равно
N =
23 = 8
Заполнение строк таблицы по этапам:
ШАГ 3
Контроль столбца
A: верхняя половина – нули, нижняя – единицы.
Слайд 69ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
3. Количество операций в выражении – 4.
Порядок их выполнения следующий:
Слайд 70ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
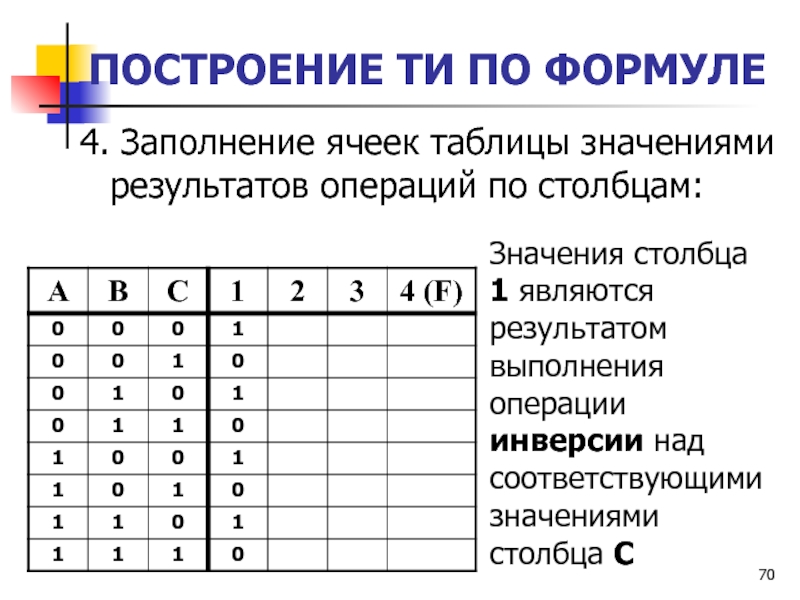
4. Заполнение ячеек таблицы значениями результатов операций
по столбцам:
Значения столбца 1 являются результатом выполнения операции инверсии
над соответствующими значениями столбца С
Слайд 71ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
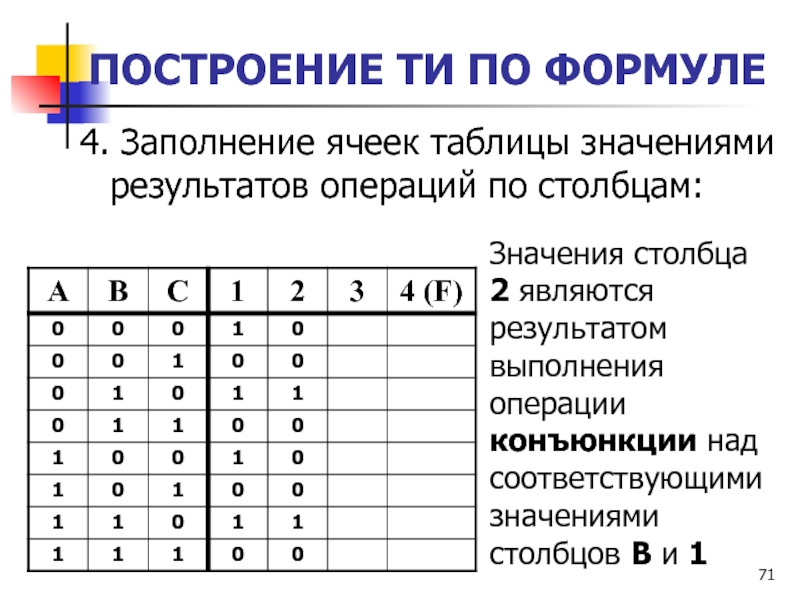
4. Заполнение ячеек таблицы значениями результатов операций
по столбцам:
Значения столбца 2 являются результатом выполнения операции конъюнкции
над соответствующими значениями столбцов B и 1
Слайд 72ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
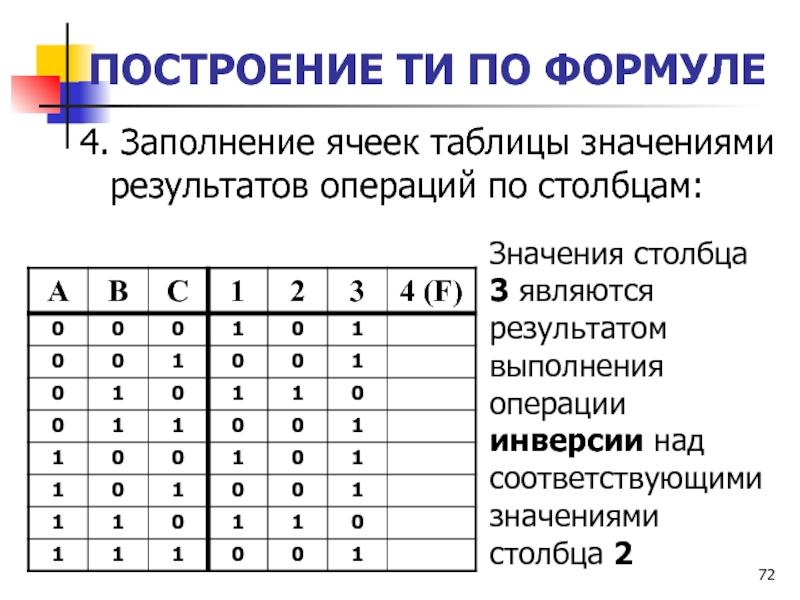
4. Заполнение ячеек таблицы значениями результатов операций
по столбцам:
Значения столбца 3 являются результатом выполнения операции инверсии
над соответствующими значениями столбца 2
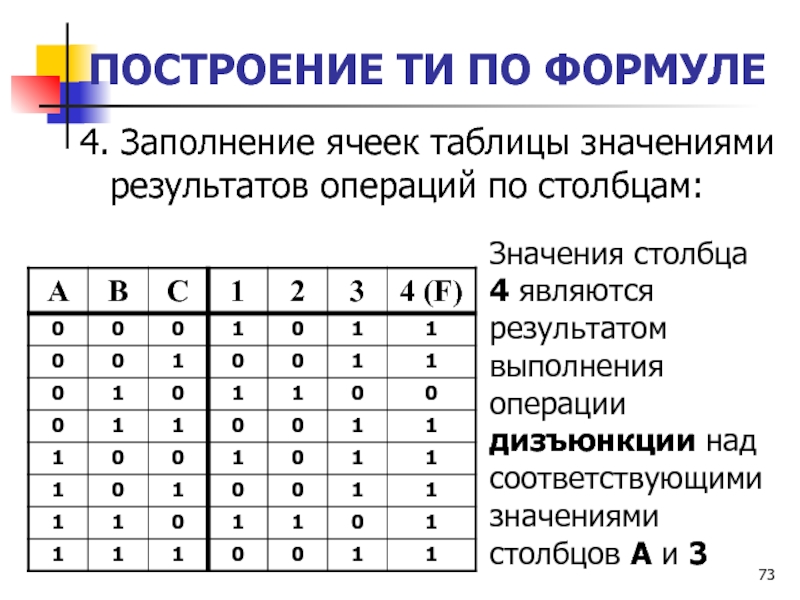
Слайд 73ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
4. Заполнение ячеек таблицы значениями результатов операций
по столбцам:
Значения столбца 4 являются результатом выполнения операции дизъюнкции
над соответствующими значениями столбцов A и 3
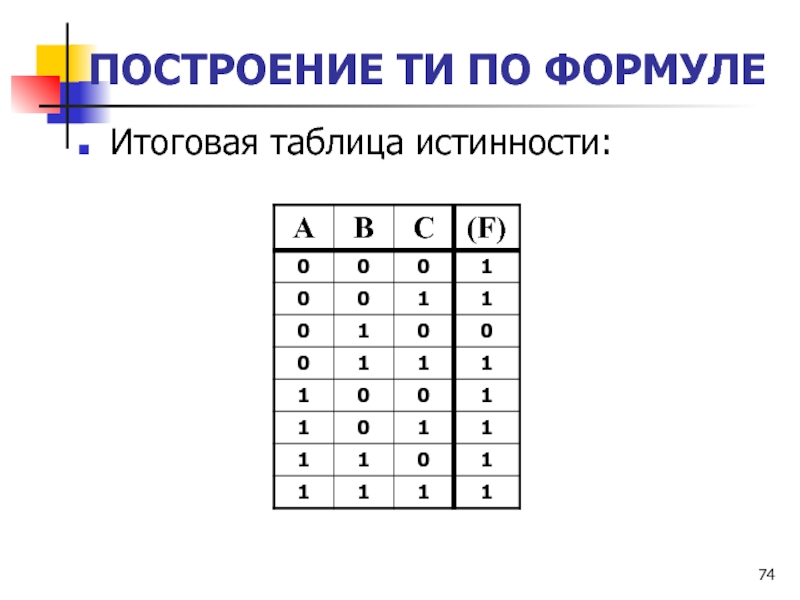
Слайд 74ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
Итоговая таблица истинности:
Слайд 75ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
Существуют формулы, в которых порядок выполнения операций
можно выстроить по-разному
Пример
Для формулы
неважно, результат какой из конъюнкций будет посчитан прежде
Слайд 76ПОСТРОЕНИЕ ТИ ПО ФОРМУЛЕ
Существуют формулы, в которых порядок выполнения операций
можно выстроить по-разному
Пример
Для формулы
неважно, результат какой из дизъюнкций будет посчитан прежде
Слайд 77ВАЖНО !!!
По сути, изменяя порядок, переходим к равносильной формуле
В
таких случаях стоит очень внимательно оценивать приоритет выполнения операций и
хорошо знать законы тождественных преобразований
Слайд 79ДОМАШНЕЕ ЗАДАНИЕ №1
В чем отличие понятий «порядок выполнения действий в
формуле» и «приоритет операций»?
Можно ли сократить первое понятие до
«порядок выполнения действий»?
Можно ли перефразировать второе понятие в «приоритет операций в формуле»?
Слайд 80ДОМАШНЕЕ ЗАДАНИЕ №1
В чем отличие понятий «формула» и «функция»?
Может
ли одна функция быть представлена несколькими формулами?
Корректен ли вопрос
«Может ли одна формула быть представлена несколькими функциями?», и если да, то ответьте на него.
Может ли одна формула представлять несколько функций?
Слайд 81ДОМАШНЕЕ ЗАДАНИЕ №1
Постройте таблицы истинности формул:
Слайд 82ДОМАШНЕЕ ЗАДАНИЕ №1
Постройте таблицы истинности формул: