Информационные технологии

свойства информации
Требует наличия
Только самой информации
Информации и ее пользователя
Информации, пользователя и

цели использования

Мера

количественной меры информации впервые предложил Р. Хартли в 1928 году
Количество

информации по формуле Хартли:

где i – количество информации (бит); N – количество элементарных сообщений.

Сам термин произошел от слияния слов binary digit - двоичная цифра

Из формулы Хартли вытекает основное определение бита

Бит равен информации, которая передается при приеме одного из двух равновероятных сообщений.

Производные единицы информации:
килобайт (кбайт, кб), мегабайт (Мбайт, Мб) гигабайт (Гбайт,

Гб) и т.д.
1 кб =1024 байта - 210 (1024) байтов.
1 Мб = 1024 кбайта = 220(1024 x 1024) байтов.
1 Гб = 1024 Мбайта - 230 (1024 х 1024 х 1024)байтов.

Бит - двоичная единица информации.

1 бит – это количество информации, которое можно получить при ответе на вопрос типа «да - нет»

Математически бит отображается состоянием 1 или 0 одного разряда двоичной системы счисления.

При получении информации в 1 бит неопределенность уменьшается в 2 раза

Другие свойства бита

семантической информации, то:
1. При SП  0 пользователь не понимает

поступающую информацию и IС  0
2. При SП   пользователю уже известна поступающая информация и IС  0

Максимальное значение IС приобретает при таком согласовании с тезаурусом пользователя SП, когда поступающая информация с одной стороны понятна пользователю, а с другой, несет ранее неизвестные ему сведения

системы, где эта информация используется
IП() = П(/) - П()
В такой

постановке единицей измерения ценности информации являются денежные единицы.

Где IП() - ценность информационного сообщения  для системы управления ;
П() - ожидаемый экономический эффект функционирования системы управления ;
П(/) - ожидаемый экономический эффект функционирования системы управления , при условии, что для управления будет использована информация, содержащаяся в сообщении .

временем
Случайный процесс общего типа
Случайный процесс с дискретным временем
Дискретный случайный процесс

с непрерывным временем

По признакам, связанным с пространством состояний и с параметром времени выделяют следующие классы случайных процессов

изменением степени неосведомленности получателя
Пусть мера неосведомленности равна H().
После

получения некоторого сообщения  неосведомленность уменьшилась и стала H(/).
Тогда количество информации I() в сообщении , определится так:

I() = H() - H(/)

Количество полученной информации измеряется уменьшением неопределенности состояния системы

обладать тем или иным алфавитом, который должен быть заранее известен

приемнику информации

3. В качестве меры неопределенности следует использовать величину равную логарифму вероятности, взятому с противоположным знаком

2. Синтаксическое количество информации зависит, по определению, только от статистических свойств появления элементов алфавита в сообщении

Этот показатель получил название
информационная энтропия

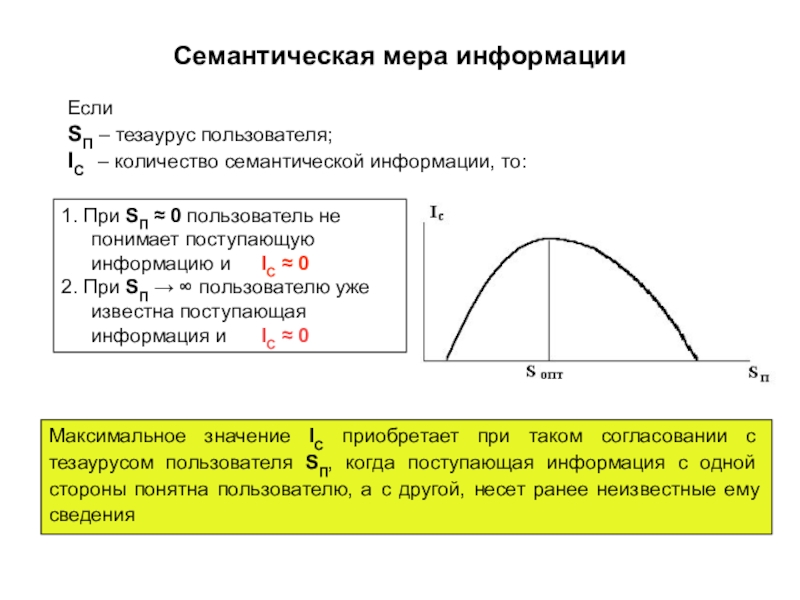
Мичиганского университета Клод Шеннон, которому было тогда 21 год, имея

два диплома бакалавра - по электротехнике и по математике, сумел ликвидировать разрыв между алгебраической теорией логики и ее практическим приложением. Свои идеи относительно связи между двоичным исчислением, булевой алгеброй и электрическими схемами Шеннон развил в докторской диссертации, опубликованной в 1938 году

В 1948 году опубликовал фундаментальную работу A Mathematical Theory of Communication, в которой сформулированы основы теории информации.

Большую ценность представляет другая работа – Communication Theory of Secrecy Systems (1949), в которой сформулированы математические основы криптографии.

C 1956 – член Национальной академии наук США и Американской академии искусств и наук.

Клод Элвуд Шеннон – один из создателей математической теории информации, в значительной мере предопределил своими результатами развитие общей теории дискретных автоматов, которые являются важными составляющими кибернетики

p(2),....p(i),.....p(N) – вероятности появления элементов алфавита x1,

x2,....xi,.....xN

Формула К. Шеннона

Для случая, когда вероятность появления для всех элементов алфавита одинакова p(1) = p(2) ...= p(N) = 1/N

H(/) при H(/) = 0 получаем:
I() =

H()

Количество информации, приносимое в среднем одним элементом (знаком) сообщения равно энтропии источника

При использовании двоичного алфавита N = 2 и p(1) = p(2) = 0,5 это количество информации равно одному биту

Так как N = mn

Если сообщение содержит n разрядов и его алфавит состоит из m различных символов то при одинаковой вероятности их появления

I = logN = nlogm

того, какой элемент xj был предшествующий, а условная вероятность их

совместного появления p(i|j), то сначала вычисляется условная энтропия

Для получения безусловной энтропии источника необходимо провести усреднение по вероятностям появления элементов

величина ограниченная
3
Энтропия равна 0,если вероятность одного из состояний источника информации

равна 1

4

Энтропия максимальна при равной вероятности всех состояний источника информации

5

Энтропия объединенных статистически независимых источников информации равна сумме их энтропий

6

Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля состояний

возможное число реализаций случайной аналоговой величины сделать конечным и равным

N, то Каждая из реализаций C1, C2,....Ci,.....CN будет иметь определенную вероятность появления. Тогда энтропия и среднее количество информации в каждой реализации определятся известным равенством