Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интеграл и его
Содержание
- 1. Интеграл и его
- 2. Функция F(x) называется первообразной функции f(x) на
- 3. Определите, является ли функция F(x)
- 4. Совокупность всех первообразных F(x) + C функции
- 5. Найдем неопределенный интеграл:
- 6. Формула Ньютона-Лейбница для вычисления определенного интеграла:
- 7. Найдем определенный интеграл:
- 8. Физический смысл определенного интеграла
- 9. Путь пройденный точкой за промежуток времени от
- 10. Дано уравнение скорости движения тела:
- 11. Геометрический смысл определенного интеграла
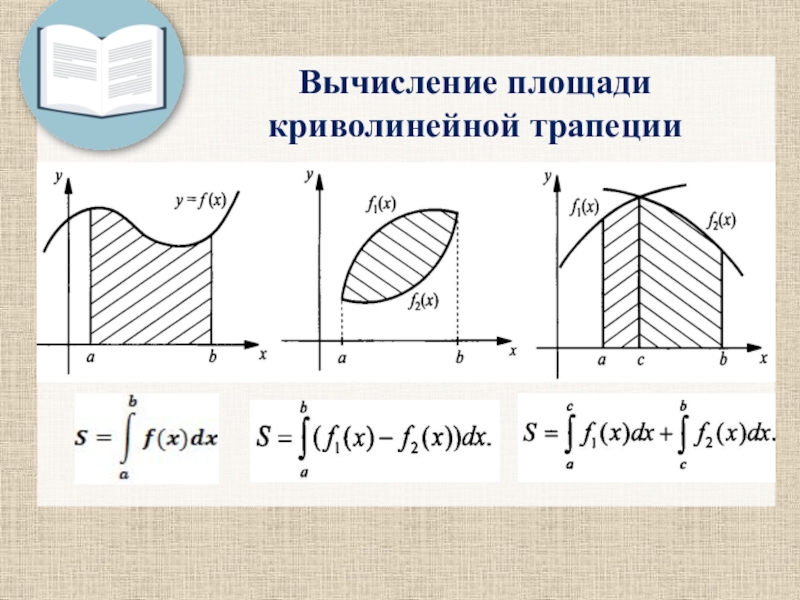
- 12. Вычисление площади криволинейной трапеции
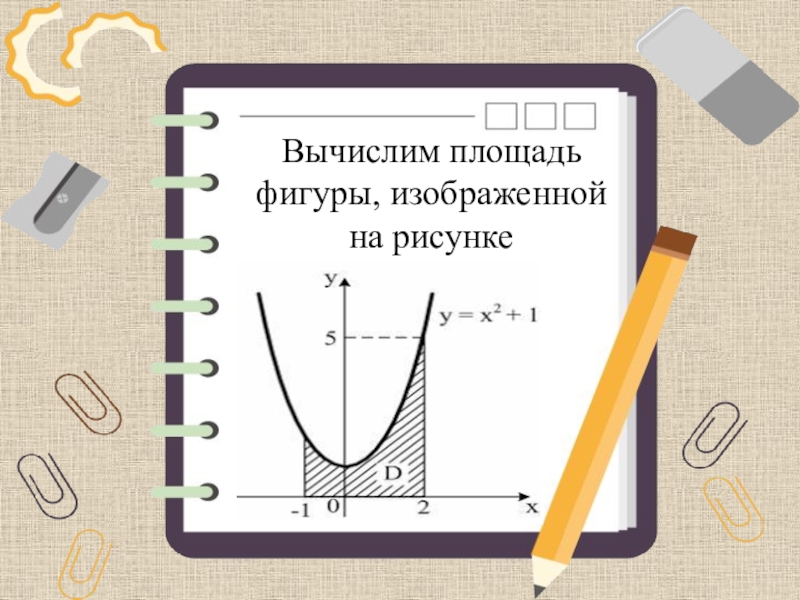
- 13. Вычислим площадь фигуры, изображенной на рисунке
- 14. Решение: Ответ: площадь фигуры составляет 6 ед2
- 15. Спасибо за внимание!
- 16. Скачать презентанцию
Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех х из этого промежутка выполняется равенство:
Слайды и текст этой презентации
Слайд 2Функция F(x) называется первообразной функции f(x) на некотором промежутке, если
для всех х из этого промежутка выполняется равенство:
Слайд 3 Определите, является ли функция F(x) = 5x4 + 12x
первообразной для функции f(x) = 12 + 20x3 ?
Решение:
Проверим,
выполняется ли свойствоFʹ(x) = (5x4 + 12x)ʹ = 5(x4)ʹ + 12(x)ʹ =
= 5 ∙ 4x3 + 12∙ 1= 20x3 + 12
Получили, что Fʹ(x) = f(x), значит
F(x) – первообразная для f(x)
Слайд 4Совокупность всех первообразных F(x) + C функции f(x) определенных на
некотором промежутке называется неопределенным интегралом и обозначается:
Слайд 9Путь пройденный точкой за промежуток времени от t = a
до t = b, равен определенному интегралу
от скорости v(t)
Слайд 10Дано уравнение скорости движения тела:
(м/с).
Найдите путь, пройденный телом
за 2 с
от начала движения.Решение:
Ответ: пройденный путь равен 16 м