Интеллектуальный анализ данных

в сырых данных ранее неизвестных, нетривиальных, практически полезных и доступных

интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности и использование обнаруженных знаний для прогнозирования.

Интеллектуальный анализ данных

регрессионный анализ, факторный анализ, дисперсионный анализ).
Многомерный статистический анализ (компонентный

анализ, дискриминантный анализ, многомерный регрессионный анализ, канонические корреляции и др.).
Анализ временных рядов (динамические модели и прогнозирование).

Методы Data Mining

аналогов, прототипов) – алгоритм Apriori
нечеткая логика
деревья решений (ID3, C4.5)
системы обработки

экспертных знаний
Кластеризация (Гюстафсон-Кессель, Fuzzy C-means)

из заранее известных классов.
Кластеризация — разделение множества входных векторов на

группы (кластеры) по степени «похожести» друг на друга.
Сокращение описания — для визуализации данных, лаконизма моделей, упрощения счета и интерпретации, сжатия объемов собираемой и хранимой информации.
Ассоциация — поиск повторяющихся образцов. Например, поиск «устойчивых связей в корзине покупателя» — вместе с пивом часто покупают орешки.
Прогнозирование
Анализ отклонений — Например, выявление нетипичной сетевой активности позволяет обнаружить вредоносные программы.
Визуализация

Задачи Data Mining

объекта на основании значений других параметров.
Определяемый параметр – зависимая переменная,

параметры участвующие в определении – независимые переменные

Задача классификации

о клиенте (возраст, пол, профессия, доход). Определенная часть клиентов, воспользовавшись

продуктом фирмы, осталась ей верна; другие клиенты больше не приобретали продукты фирмы. На этом уровне мы определяем тип задачи - это задача классификации.
На втором уровне определяем действие - прогностическое моделирование. С помощью прогностического моделирования мы с определенной долей уверенности можем отнести новый объект, в данном случае, нового клиента, к одному из известных классов - постоянный клиент, или это, скорее всего, его разовая покупка.
На третьем уровне мы можем воспользоваться приложением для принятия решения. В результате приобретения знаний, фирма может существенно снизить расходы, например, на рекламу, зная заранее, каким из клиентов следует активно рассылать рекламные материалы.

Пример (определения надежности клиентов фирмы)

результатов на основании других наборов данных
Модели классификации – описывают правила

или наборы правил, в соответствии с которыми можно отнести описание любого нового объекта к одному из классов
Модели последовательностей – описывают функции, позволяющие прогнозировать изменение непрерывных числовых параметров.

Модели Data Mining

факторов
Регрессионные модели – описывают функциональные зависимости между зависимыми и независимыми

показателями и переменными в понятной человеку форме
Модели кластеров – описывают группы, на которые можно разделить объекты, данные о которых подвергаются анализу. Группируются объекты на основе данных, описывающих сущность объектов

отличаются чем-либо от основного множества записей
Итоговые модели – выявление ограничений

на данные анализируемого массива
Ассоциативные модели – выявление закономерностей между связанными событиями

структуре, где каждому объекту соответствует единственный узел, дающий решение.
Под правилом

понимается логическая конструкция, представленная в виде "если ... то ...".
Большинство из известных алгоритмов являются "жадными алгоритмами". Если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой атрибут, который дал бы лучшее разбиение. И поэтому на этапе построения нельзя сказать даст ли выбранный атрибут, в конечном итоге, оптимальное разбиение.

Деревья решений

CART, C4.5, NewId, ITrule, CHAID, CN2 и т.д. Но наибольшее

распространение и популярность получили следующие два:
CART (Classification and Regression Tree) – это алгоритм построения бинарного дерева решений – дихотомической классификационной модели. Каждый узел дерева при разбиении имеет только двух потомков. Как видно из названия алгоритма, решает задачи классификации и регрессии.
C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации.

формализовать свои знания;
извлечение правил на естественном языке;
интуитивно понятная

классификационная модель;
высокая точность прогноза, сопоставимая с другими методами (статистика, нейронные сети);
построение непараметрических моделей.

Преимущества

функция оценки качества разбиения;
механизм отсечения дерева;
алгоритм обработки пропущенных значений;
построение деревьев

регрессии.

Алгоритм CART

построения дерева правило, формируемое в узле, делит заданное множество примеров

(обучающую выборку) на две части – часть, в которой выполняется правило (потомок – right) и часть, в которой правило не выполняется (потомок – left). Для выбора оптимального правила используется функция оценки качества разбиения.

Бинарное представление

с числом примеров в каждом N1 и N2 соответственно, тогда

показатель качества разбиения будет равен


Наилучшим считается то разбиение, для которого Ginisplit(T) минимально.
Обозначим N – число примеров в узле – предке, L, R – число примеров соответственно в левом и правом потомке, li и ri – число экземпляров i-го класса в левом/правом потомке. Тогда качество разбиения оценивается по следующей формуле:

xi

всего выбирается как среднее арифметическое двух соседних упорядоченных значений переменной xi обучающей выборки. Если переменная категориального типа, то в узле формируется правило xi V(xi), где V(xi) – некоторое непустое подмножество множества значений переменной xi в обучающей выборке.
На каждом шаге построения дерева алгоритм последовательно сравнивает все возможные разбиения для всех атрибутов и выбирает наилучший атрибут и наилучшее разбиение для него.

Правила разбиения

с общим предком, которые могут быть объединены, т.е. отсечены в

родительский узел без увеличения ошибки классификации. R(t) = R(l) + R(r), где r и l – листы узла t. Продолжать пока таких пар больше не останется. Так мы получим дерево, имеющее такую же стоимость как Tmax при = 0, но менее ветвистое, чем Tmax

посредством тестирования на тестовой выборке. Естественно, качество тестирования во многом

зависит от объема тестовой выборки и 'равномерности' данных, которые попали в обучающую и тестовую выборки.

Выбор финального дерева

встречающиеся наборы элементов, а затем, на втором, извлечь из них

правила. Количество элементов в наборе будем называть размером набора, а набор, состоящий из k элементов, – k-элементным набором.

Алгоритм Apriori

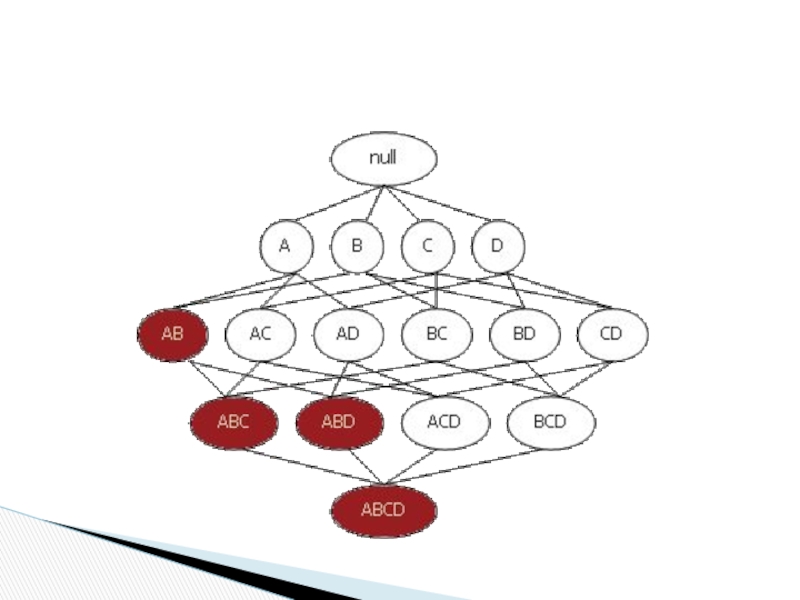
ресурсов и, соответственно, времени. Примитивный подход к решению данной задачи

– простой перебор всех возможных наборов элементов. Apriori использует одно из свойств поддержки, гласящее: поддержка любого набора элементов не может превышать минимальной поддержки любого из его подмножеств.
Например, поддержка 3-элементного набора {Хлеб, Масло, Молоко} будет всегда меньше или равна поддержке 2-элементных наборов {Хлеб, Масло}, {Хлеб, Молоко}, {Масло, Молоко}. Дело в том, что любая транзакция, содержащая {Хлеб, Масло, Молоко}, также должна содержать {Хлеб, Масло}, {Хлеб, Молоко}, {Масло, Молоко}, причем обратное не верно.
Это свойство носит название анти-монотонности и служит для снижения размерности пространства поиска.

решетки, начинающейся с пустого множества, затем на 1 уровне 1-элементные

наборы, на 2-м – 2-элементные и т.д. На k уровне представлены k-элементные наборы, связанные со всеми своими (k-1)-элементными подмножествами.
На первом шаге алгоритма подсчитываются 1-элементные часто встречающиеся наборы. Для этого необходимо пройтись по всему набору данных и подсчитать для них поддержку, т.е. сколько раз встречается в базе.
Следующие шаги будут состоять из двух частей: генерации потенциально часто встречающихся наборов элементов (их называют кандидатами) и подсчета поддержки для кандидатов.

k++) {
Ck = Apriorigen(Fk-1) // генерация кандидатов
для всех транзакций t∈T

{
Ct = subset(Ck, t) // удаление избыточных правил
для всех кандидатов c ∈ Ct
c.count ++
}
Fk = { c ∈ Ck | c.count >= minsupport} // отбор кандидатов
}
Результат ∪Fk

Общее описание алгоритма

набора размера (k-1) добавлением элемента из другого (k-1)- элементного набора. Алгоритм

этой функции Apriorigen в виде небольшого SQL-подобного запроса. insert into Ck select p.item1, p.item2, …, p.itemk-1, q.itemk-1 From Fk-1 p, Fk-1 q where p.item1= q.item1, p.item2 = q.item2, … , p.itemk-2 = q.itemk-2, p.itemk-1 < q.itemk-1
Удаление избыточных правил. На основании свойства анти-монотонности, следует удалить все наборы c Ck если хотя бы одно из его (k-1) подмножеств не является часто встречающимся.

Генерация кандидатов

дерева содержат хэш-таблицы с указателями на потомков, а листья –

на кандидатов.
Хэш-дерево строится каждый раз, когда формируются кандидаты. Первоначально дерево состоит только из корня, который является листом, и не содержит никаких кандидатов-наборов. Каждый раз когда формируется новый кандидат, он заносится в корень дерева и так до тех пор, пока количество кандидатов в корне-листе не превысит некоего порога. Как только количество кандидатов становится больше порога, корень преобразуется в хэш-таблицу, т.е. становится внутренним узлом, и для него создаются потомки-листья. И все примеры распределяются по узлам-потомкам согласно хэш-значениям элементов, входящих в набор, и т.д. Каждый новый кандидат хэшируется на внутренних узлах, пока он не достигнет первого узла-листа, где он и будет храниться, пока количество наборов опять же не превысит порога.

Подсчет поддержки каждого кандидата

нужно "пропустить" каждую транзакцию через дерево и увеличить счетчики для

тех кандидатов, чьи элементы также содержатся и в транзакции. На корневом уровне хэш-функция применяется к каждому элементу из транзакции. Далее, на втором уровне, хэш-функция применяется ко вторым элементам и т.д. На k-уровне хэшируется k-элемент. И так до тех пор, пока не достигнем листа. Если кандидат, хранящийся в листе, является подмножеством рассматриваемой транзакции, тогда увеличиваем счетчик поддержки этого кандидата на единицу.

через дерево, можно проверить удовлетворяют ли значения поддержки кандидатов минимальному

порогу. Кандидаты, для которых это условие выполняется, переносятся в разряд часто встречающихся. Кроме того, следует запомнить и поддержку набора, она нам пригодится при извлечении правил. Эти же действия применяются для нахождения (k+1)-элементных наборов и т.д.

множества, лежащего в условии правила. Например, имеется часто встречающийся набор

{A, B, C} и требуется подсчитать достоверность для правила AB->C. Поддержка самого набора нам известна, но и его множество {A, B}, лежащее в условии правила, также является часто встречающимся в силу свойства анти-монотонности, и значит его поддержка нам известна. Тогда мы легко сможем подсчитать достоверность.
Чтобы извлечь правило из часто встречающегося набора F, следует найти все его непустые подмножества. И для каждого подмножества s мы сможем сформулировать правило s->(F – s), если достоверность правила conf(s->(F – s)) = supp(F)/supp(s) не меньше порога minconf.

Генерация правил

если знаменатель имеет максимальное значение, а это происходит в том

случае, когда в условии правила имеется набор, состоящий из одного элемента. Все супермножества данного множества имеют меньшую или равную поддержку и, соответственно, большее значение достоверности. Это свойство может быть использовано при извлечении правил. Если мы начнем извлекать правила, рассматривая сначала только один элемент в условии правила, и это правило имеет необходимую поддержку, тогда все правила, где в условии стоят супермножества этого элемента, также имеют значение достоверности выше заданного порога.