Слайд 1Лектор – Юшко Сергей Владимирович
кафедра ИКГиАП
ауд. Д-504
ИНЖЕНЕРНАЯ ГРАФИКА
Слайд 2Инженерная графика – дисциплина, изучающая вопросы изображения изделий на плоскости.
Целями
освоения дисциплины «Инженерная графика» являются
а) формирование знаний о
способах отображения пространственных форм на плоскости, о правилах выполнения чертежей,
б) обучение технологии построения чертежей,
в) обучение способам применения пакета графических программ для изготовления и редактирования чертежей,
г) раскрытие сущности процессов, составляющих проектно-конструкторскую компетентность современного специалиста в инновационной экономике.
Слайд 3В результате освоения дисциплины обучающийся должен:
Знать:
а) способы отображения
пространственных форм на плоскости,
б) правила и условности при выполнении
чертежей
2) Уметь:
а) выполнять и читать чертежи технических изделий и схем технологических процессов,
б) использовать средства компьютерной графики для изготовления чертежей
3) Владеть:
а) способами и приемами изображения предметов на плоскости,
б) одной из графических систем
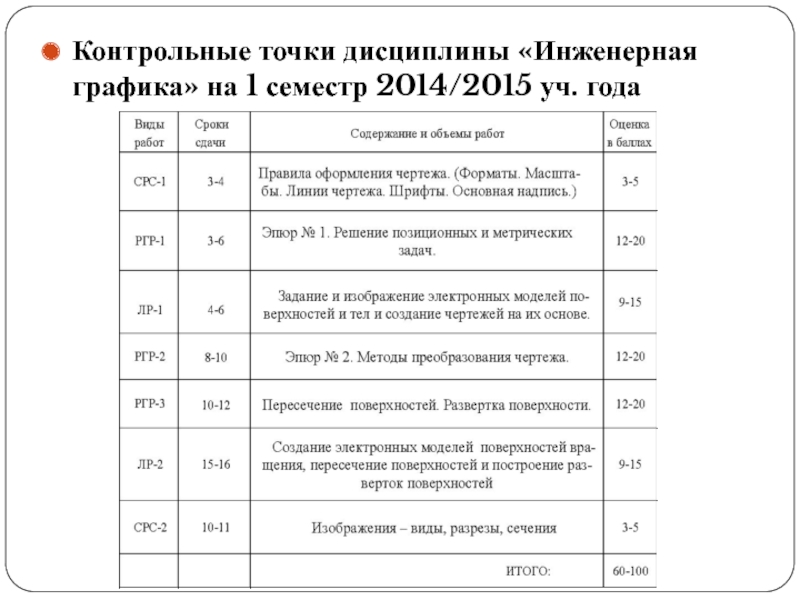
Слайд 4Контрольные точки дисциплины «Инженерная графика» на 1 семестр 2014/2015 уч.
года
Слайд 5СРС №1. Правила оформления чертежа
ГОСТ 2.301-68 -Форматы
ГОСТ 2.302-68 - Масштабы
ГОСТ
2.303-68 - Линии
ГОСТ 2.304-81 - Шрифты
ГОСТ 2.104-2006 – Основные надписи
GOSTEDU.ru
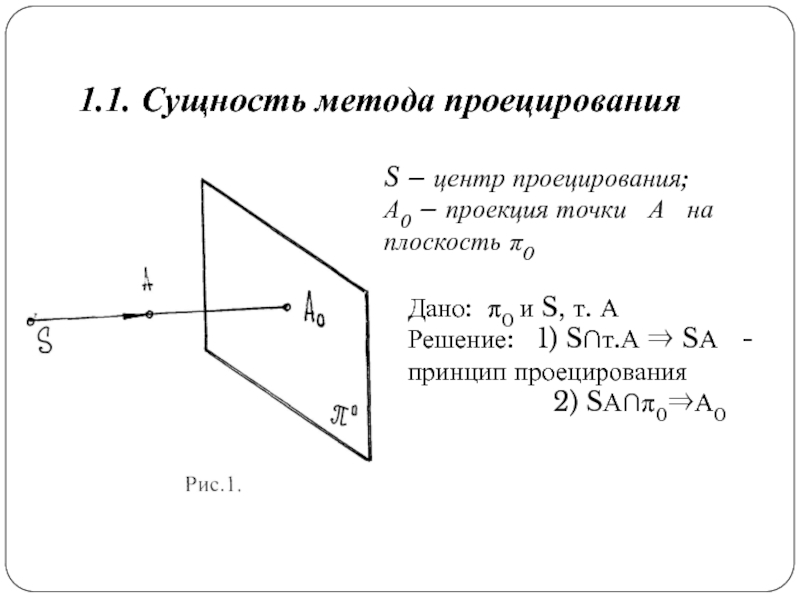
Слайд 61.1. Сущность метода проецирования
S – центр проецирования;
А0 – проекция точки
А на плоскость π0
Дано: π0 и S, т.
А
Решение: 1) S∩т.А SА - принцип проецирования
2) SА∩π0А0
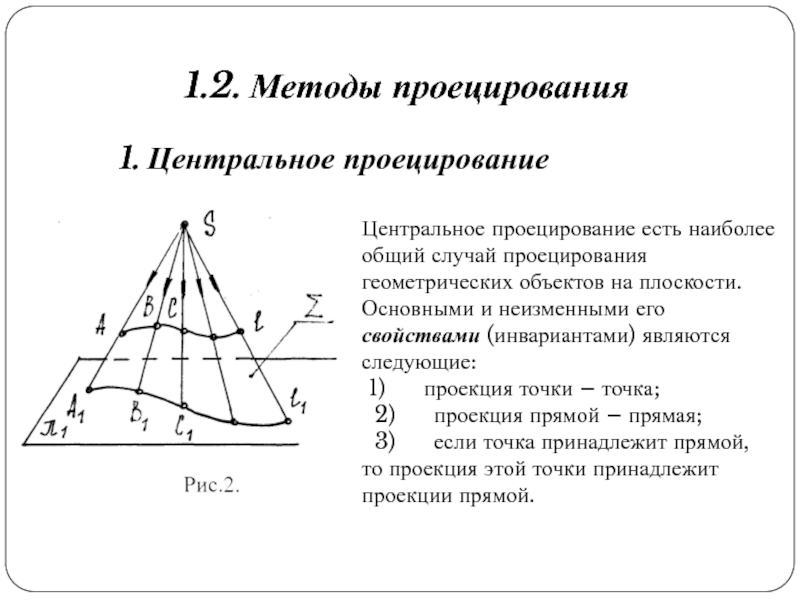
Слайд 71.2. Методы проецирования
1. Центральное проецирование
Центральное проецирование есть наиболее общий случай
проецирования геометрических объектов на плоскости.
Основными и неизменными его свойствами
(инвариантами) являются следующие:
1) проекция точки – точка;
2) проекция прямой – прямая;
3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.
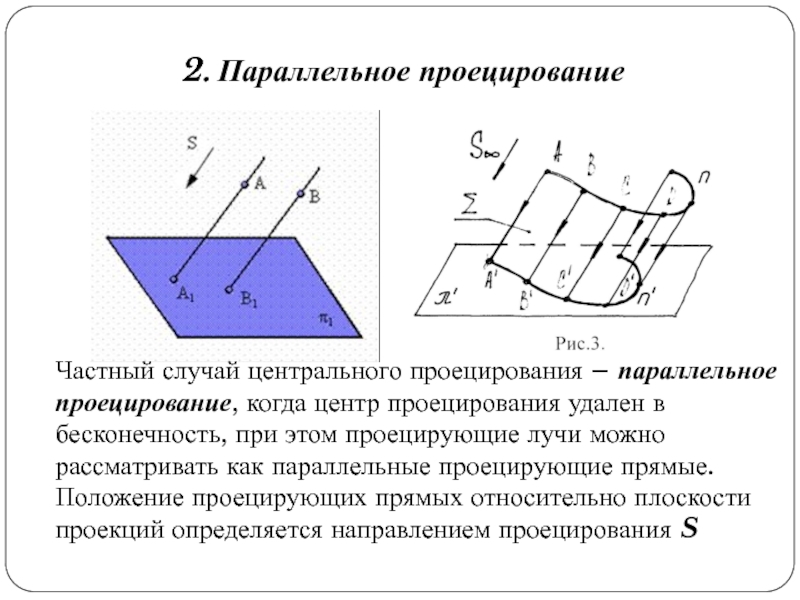
Слайд 82. Параллельное проецирование
Частный случай центрального проецирования – параллельное проецирование, когда
центр проецирования удален в бесконечность, при этом проецирующие лучи можно
рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S
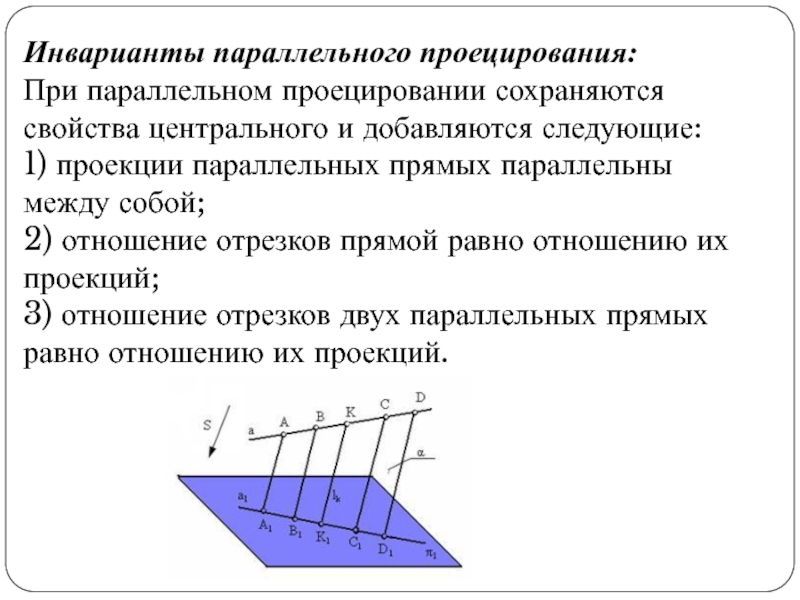
Слайд 9Инварианты параллельного проецирования:
При параллельном проецировании сохраняются свойства центрального и добавляются
следующие:
1) проекции параллельных прямых параллельны между собой;
2) отношение отрезков
прямой равно отношению их проекций;
3) отношение отрезков двух параллельных прямых равно отношению их проекций.
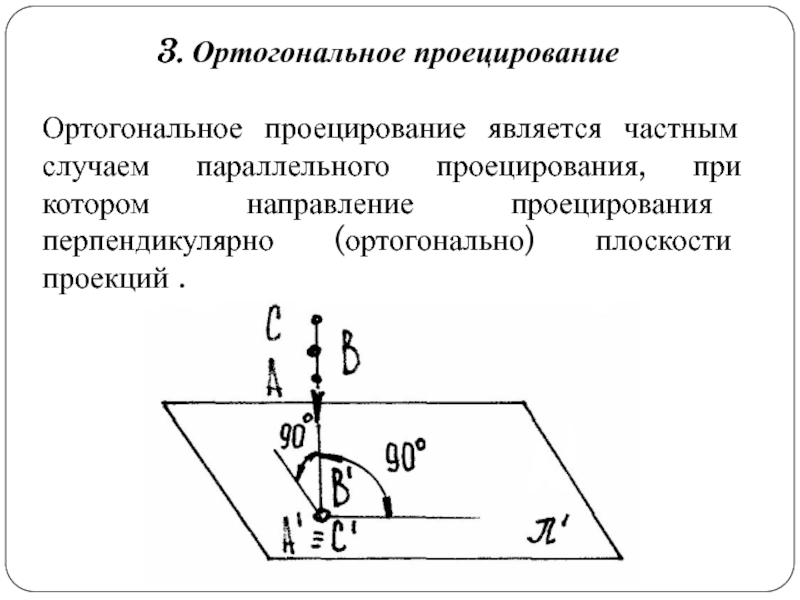
Слайд 10Ортогональное проецирование является частным случаем параллельного проецирования, при котором направление
проецирования перпендикулярно (ортогонально) плоскости проекций .
3. Ортогональное проецирование
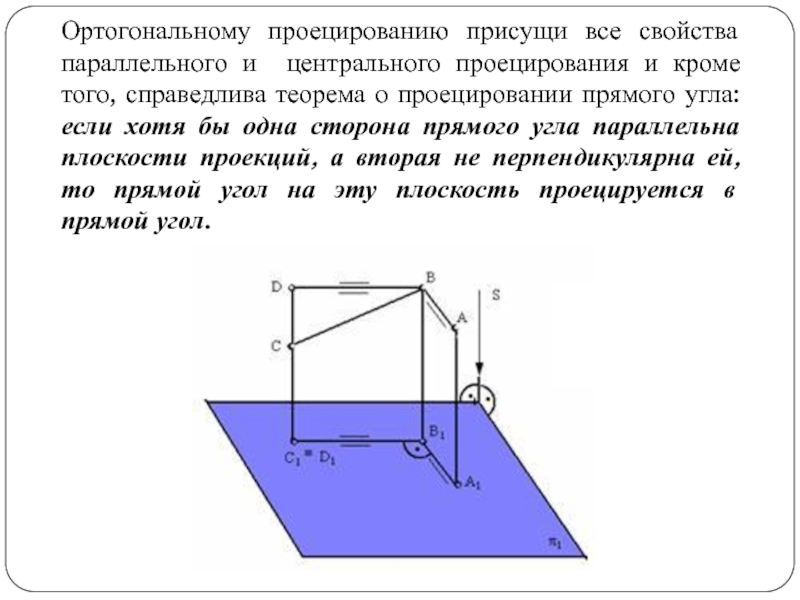
Слайд 11Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и
кроме того, справедлива теорема о проецировании прямого угла: если хотя
бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.
Слайд 12 К проекционным изображениям в начертательной геометрии предъявляются следующие основные
требования:
1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу)
– возможность определять форму и размеры объекта, его положение и связь с окружающей средой;
2. Наглядность – чертеж должен создавать пространственное представление о форме предмета;
3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты;
4. Простота – изображение должно быть простым по построению и должно допускать однозначное описание объекта в виде последовательности графических операций.
Слайд 13Гаспар Монж (10.5.1746-28.7.1818)- французский геометр и общественный деятель, Член Парижской
Академии Наук.
По праву считается создателем начертательной геометрии.
В 1799г. издал
трактат «Ceometrie descriptive» - «Начертательная геометрия»
1.3. Система трех плоскостей проекций.
Эпюр Монжа
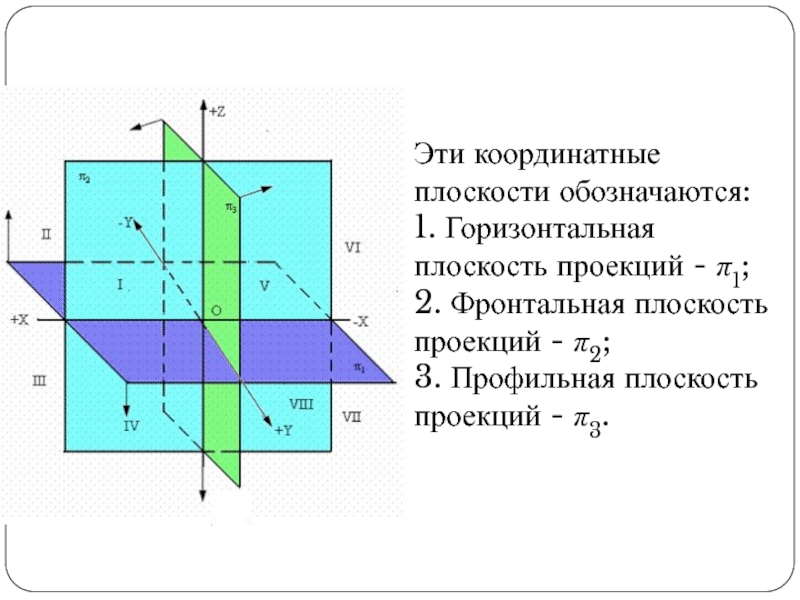
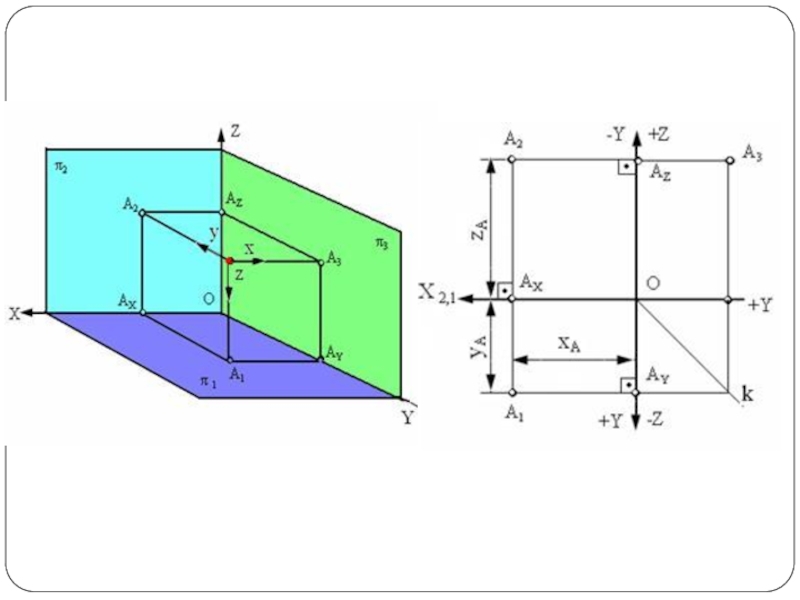
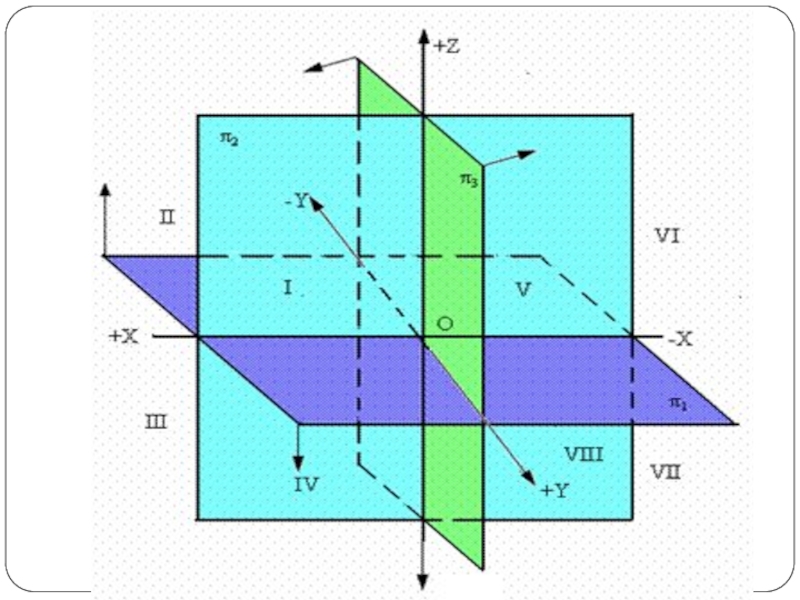
Слайд 14Эти координатные плоскости обозначаются:
1. Горизонтальная плоскость проекций - π1;
2. Фронтальная плоскость
проекций - π2;
3. Профильная плоскость проекций - π3.
Слайд 17Для построения плоской модели пространственной геометрической фигуры каждая ее точка
проецируется ортогонально на плоскости проекций π1, π2 и π3, которые затем
совмещаются в одну плоскость.
Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром Монжа.
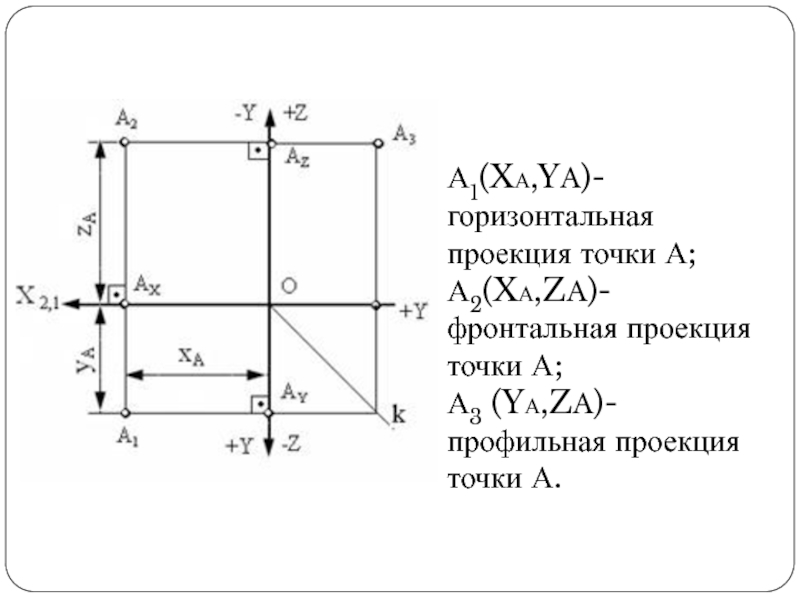
Слайд 18А1(XА,YA)- горизонтальная проекция точки А;
А2(XА,ZA)- фронтальная проекция точки А;
А3 (YА,ZA)- профильная
проекция точки А.
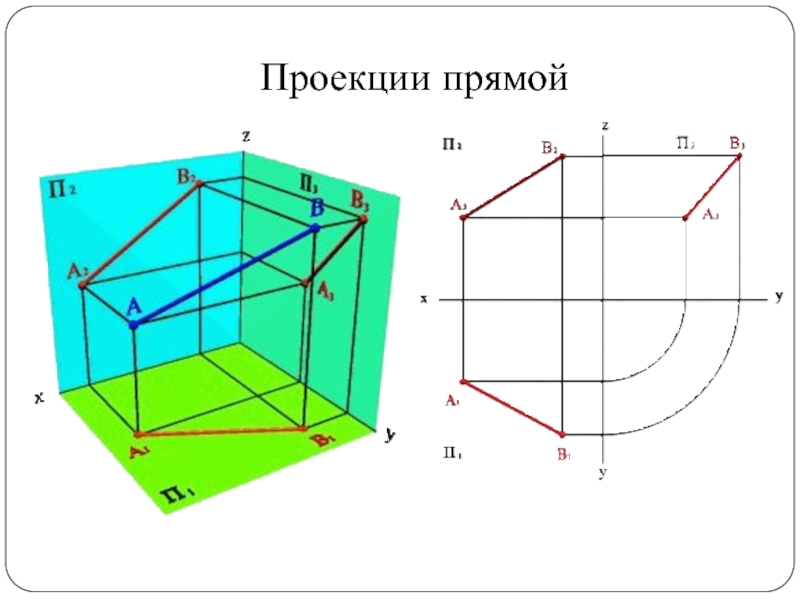
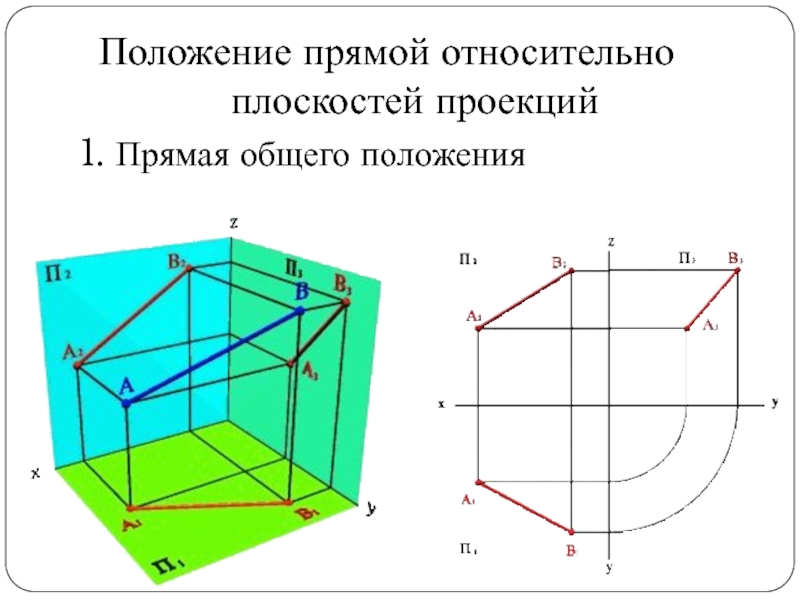
Слайд 20Положение прямой относительно
плоскостей проекций
1. Прямая общего положения
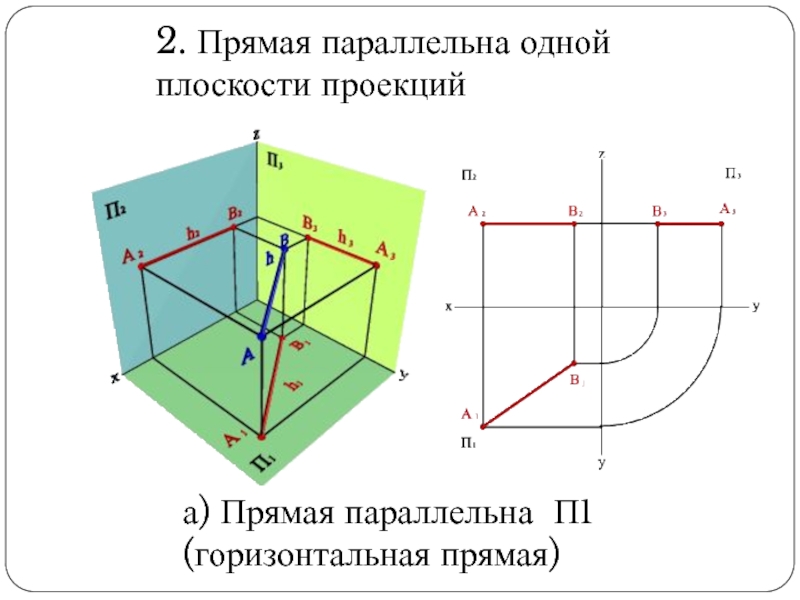
Слайд 212. Прямая параллельна одной
плоскости проекций
а) Прямая параллельна П1
(горизонтальная прямая)
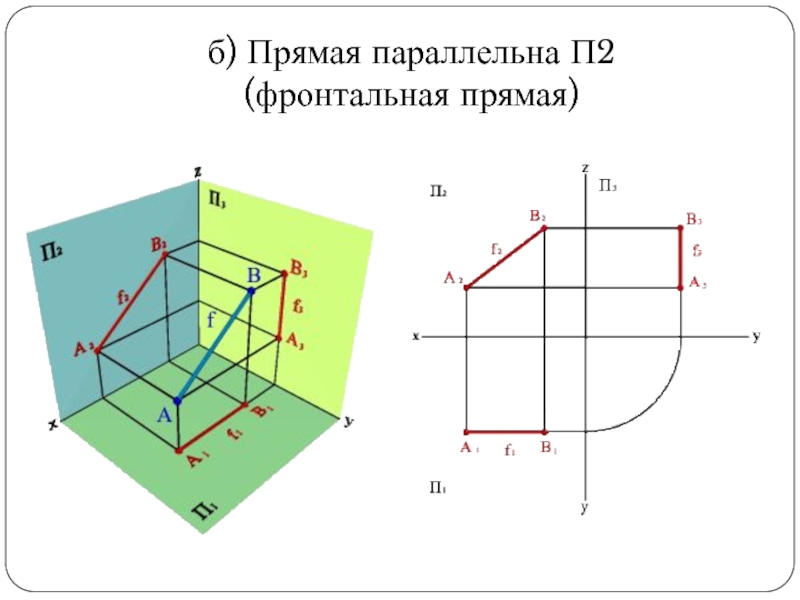
Слайд 22б) Прямая параллельна П2
(фронтальная прямая)
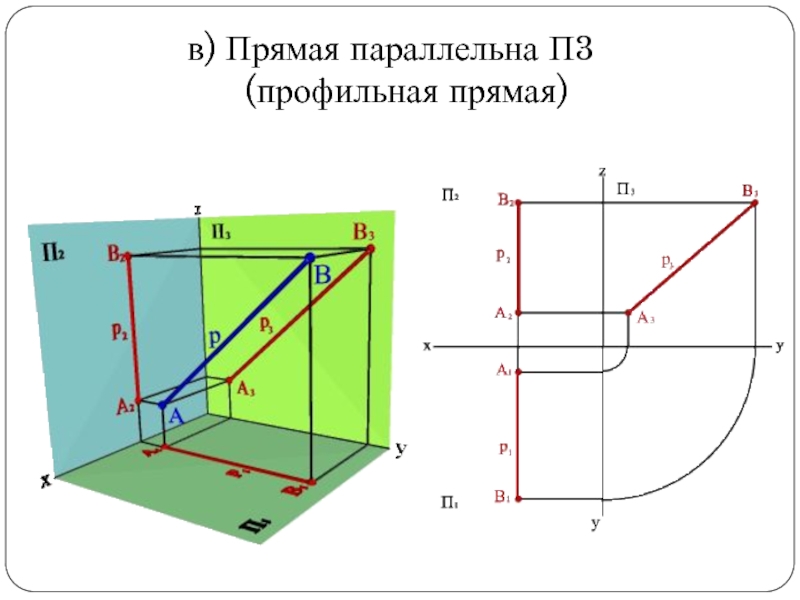
Слайд 23в) Прямая параллельна П3
(профильная прямая)
Слайд 243. Прямая параллельна двум
плоскостям проекций,
т.е. перпендикулярна третьей.
Такие прямые
называют проецирующими
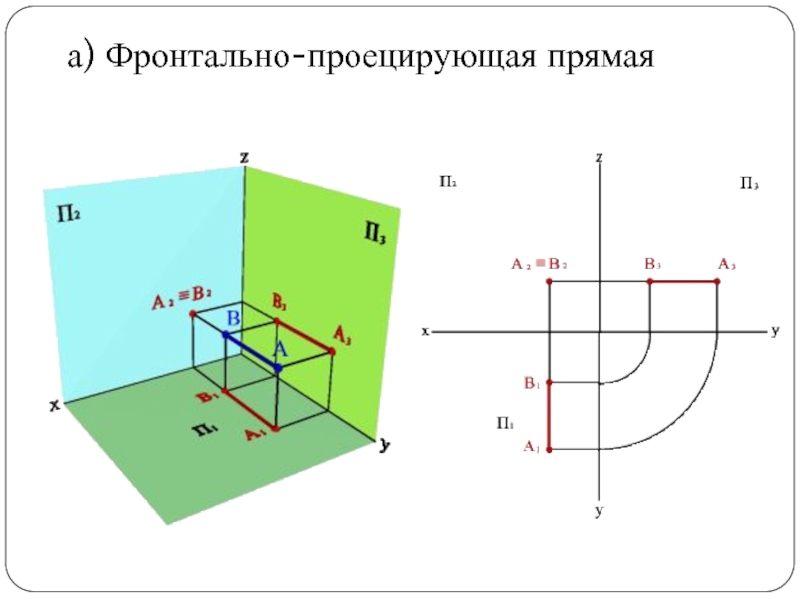
Слайд 25а) Фронтально-проецирующая прямая
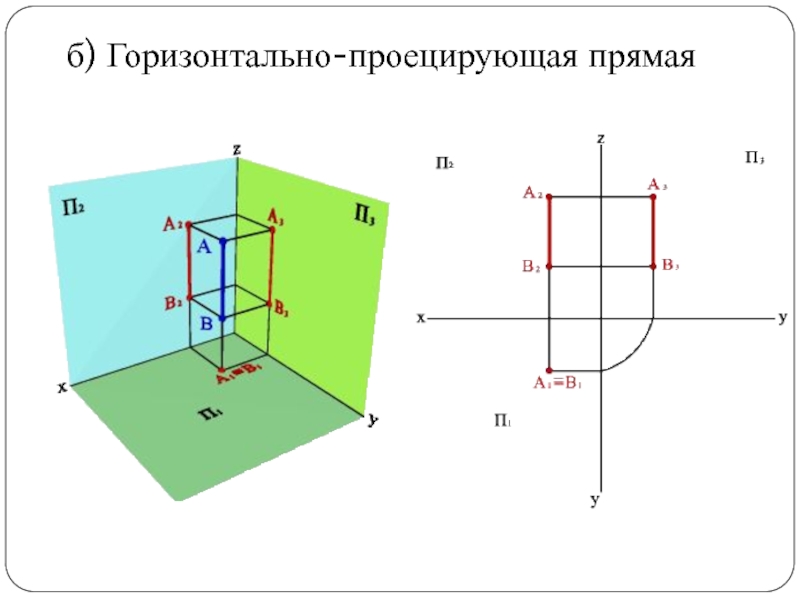
Слайд 26б) Горизонтально-проецирующая прямая
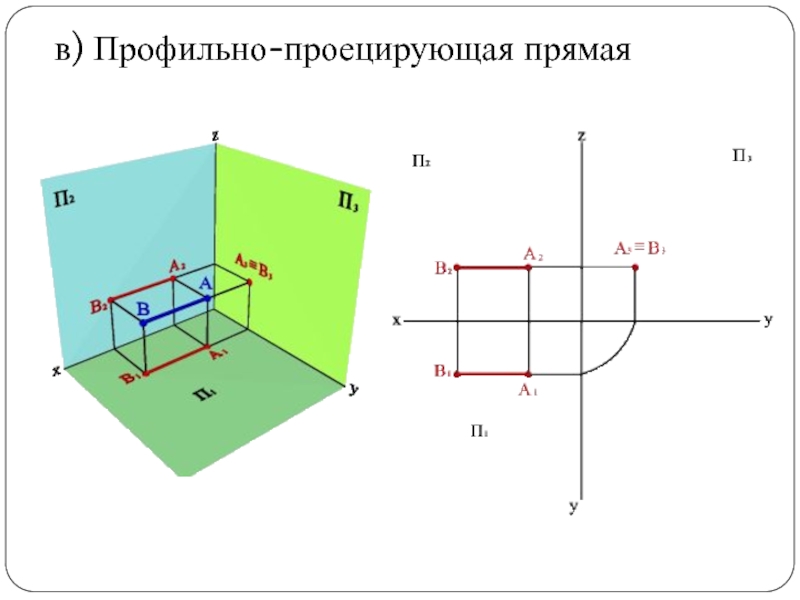
Слайд 27в) Профильно-проецирующая прямая
Слайд 28Взаимное расположение точки и прямой
Если точка принадлежит прямой,
то её
проекции должны принадлежать
одноименным проекциям этой прямой
(аксиома принадлежности точки
прямой)
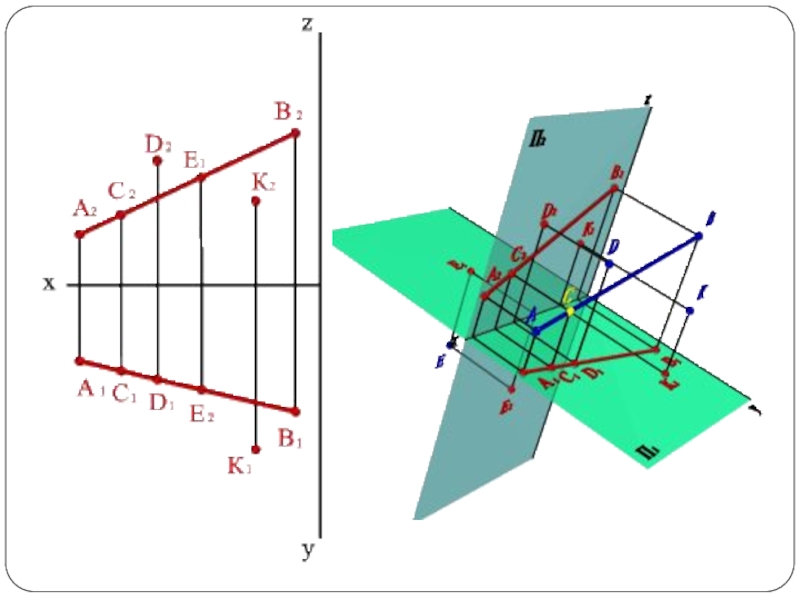
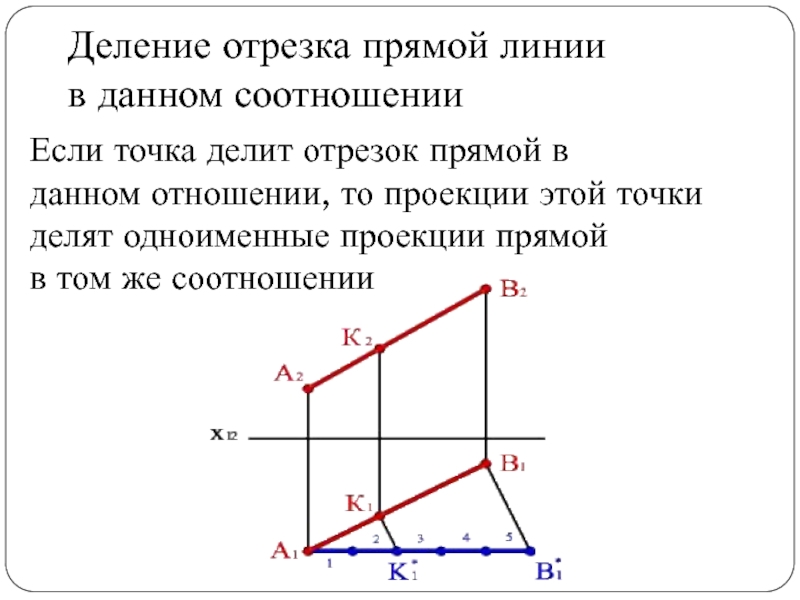
Слайд 30Деление отрезка прямой линии
в данном соотношении
Если точка делит отрезок
прямой в
данном отношении, то проекции этой точки
делят одноименные
проекции прямой
в том же соотношении
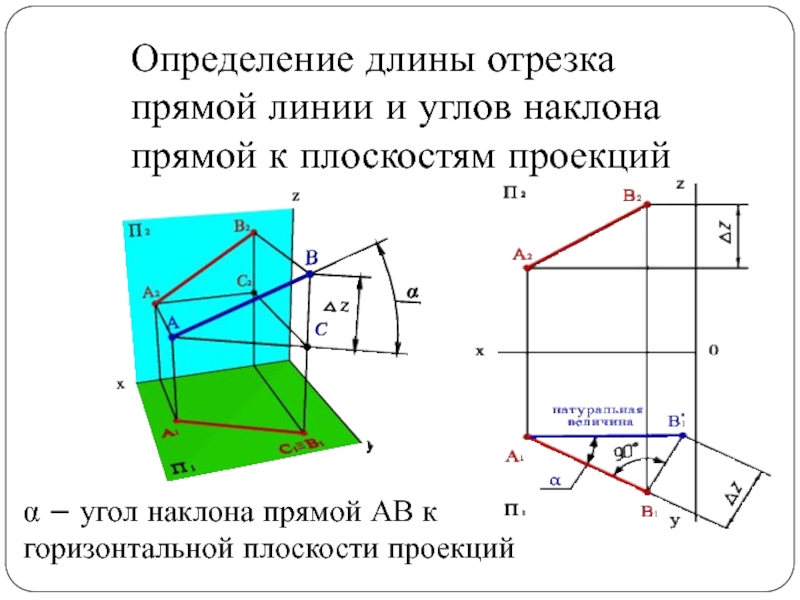
Слайд 31Определение длины отрезка
прямой линии и углов наклона
прямой к
плоскостям проекций
α – угол наклона прямой АВ к
горизонтальной плоскости
проекций
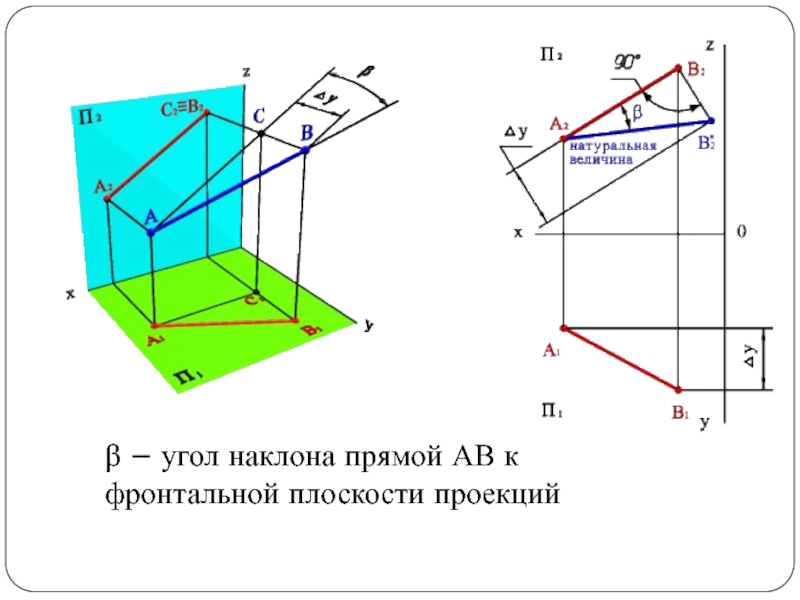
Слайд 32β – угол наклона прямой АВ к
фронтальной плоскости проекций
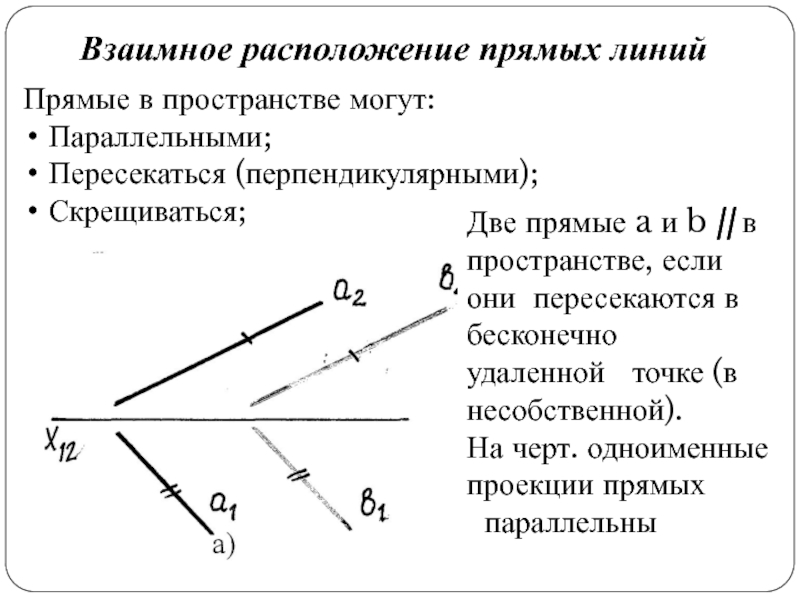
Слайд 33Взаимное расположение прямых линий
Прямые в пространстве могут:
Параллельными;
Пересекаться (перпендикулярными);
Скрещиваться;
Две прямые a
и b || в пространстве, если они пересекаются в бесконечно
удаленной
точке (в несобственной).
На черт. одноименные проекции прямых
параллельны
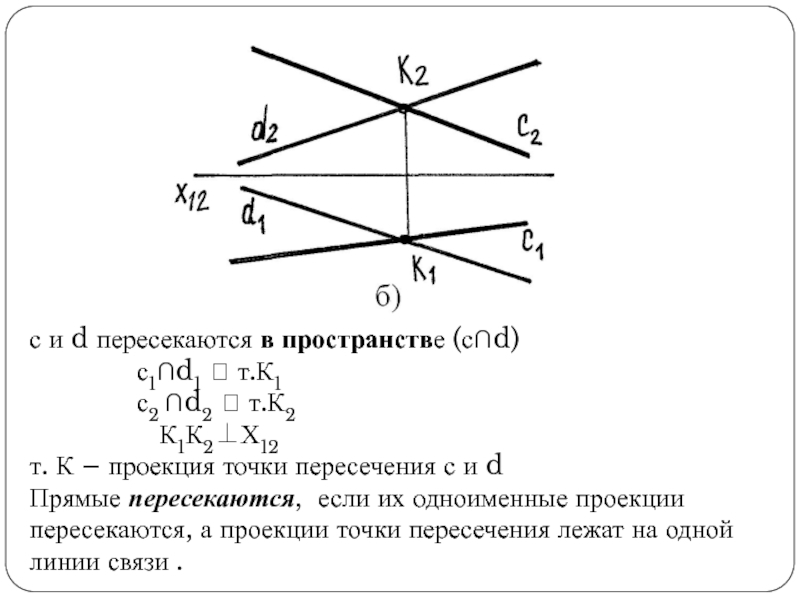
Слайд 34с и d пересекаются в пространстве (с∩d)
с1∩d1 т.К1
с2 ∩d2 т.К2
К1К2Х12
т. К – проекция точки пересечения с и d
Прямые пересекаются, если их одноименные проекции пересекаются, а проекции точки пересечения лежат на одной линии связи .
Слайд 35ℓ и m – скрещивающиеся прямые,
т.к.
ℓ 2 ∩ m2 т.12 ≡ т.22 ,
т.1 т.2
Прямые скрещиваются, если они не пересекаются и не параллельны между собой, а точки пересечения их одноимённых проекций не лежат на одной линии связи.
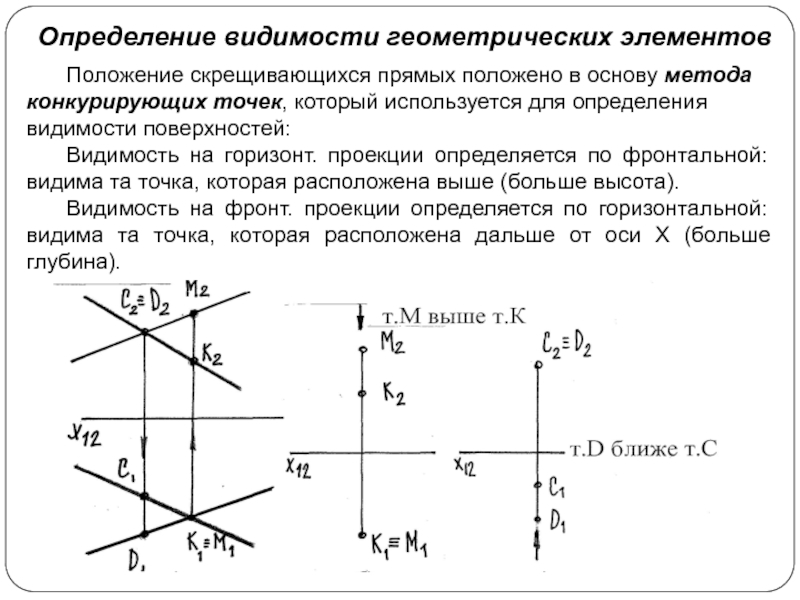
Слайд 36Положение скрещивающихся прямых положено в основу метода конкурирующих точек, который
используется для определения видимости поверхностей:
Видимость на горизонт. проекции определяется
по фронтальной: видима та точка, которая расположена выше (больше высота).
Видимость на фронт. проекции определяется по горизонтальной: видима та точка, которая расположена дальше от оси Х (больше глубина).
Определение видимости геометрических элементов