Используются материалы из: Фадд e ев М.А., Чупрунов Е.В. Лекции по атомной

физике (2008, Физматлит).
Волновая механика Шредингера вскоре была дополнена рядом новых

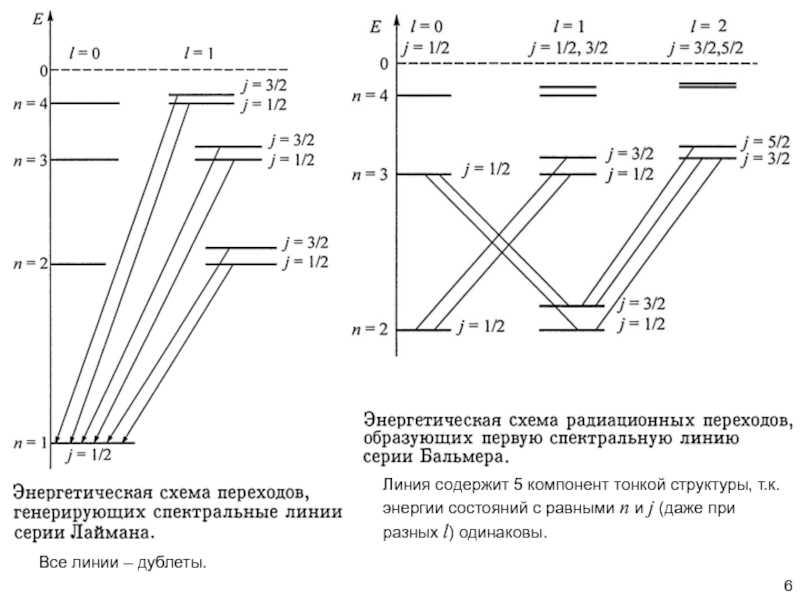
положений, что позволило корректно описать магнитные свойства атомов, «тонкую структуру» атомных спектров, а также свойства многоэлектронных атомов – все то, что не могло быть описано «старой квантовой теорией».
Одно из таких дополнений состояло во введении понятия «спина» -- собственного, «внутреннего» момента количества движения микрообъектов.
Еще в 1925 г. была выдвинута гипотеза о вращении электрона вокруг своей оси («spin»), что, в принципе, могло бы позволить объяснить наличие у него собственного момента импульса и магнитного момента. Это потребовалось для объяснения дублетной структуры оптических спектров щелочных металлов и результатов экспериментов по изучению магнетизма атомов – опыта Штерна-Герлаха и др.
Однако численные оценки показали несостоятельность этого предположения – для получения магнитного момента, равного магнетону Бора, требовалось предположить либо большой радиус электрона, либо сверхсветовую скорость вращательного движения.

6.9. Спин. Фермионы и бозоны. Принцип Паули. Многоэлектронные атомы.

спина в квантовую механику. Спин рассматривается как собственный момент импульса

микрообъекта, не связанный с ни с перемещением, ни с вращением в пространстве. Изменение величины его проекции на выделенное направление представляет собой «внутреннюю степень свободы», дополнительную по отношению к координатам. Уравнение Шредингера, специальным образом дополненное для учета наличия этой степени свободы, получило название «уравнения Паули».
(В 1928 г. Дирак показал, что существование спина следует из релятивистской теории.)

Wolfgang Ernst Pauli (1900-1958)

Каждый микрообъект характеризуется параметром s, обычно (не вполне корректно) называемым спином. Это его инвариант, наряду с массой покоя и зарядом.
Число возможных проекций «внутреннего» момента количества движения (собственных значений Sz оператора проекции спина, различающихся на ħ), для объекта равняется 2s+1 . Это целое число, поэтому s может быть лишь целым или полуцелым.
Для электрона s=1/2, что соответствует двум значениям проекции момента импульса Sz= ħ/2.

бозонами.
Помимо электрона, фермионами являются протон и нейтрон. Для них, как

и для электрона, s=1/2.
Фотон является бозоном с s=1, проекции момента импульса Sz=ħ (для частиц без массы покоя нулевое значение запрещено).
Помимо момента импульса, со спином связан и магнитный момент. Раздвоение линий в опыте Штерна-Герлаха было связано именно со спиновым магнитным моментом.
В атомах спиновые и орбитальные магнитные моменты взаимодействуют между собой и с электрическим полем ядра. В проведенном рассмотрении состояний атома водорода такое взаимодействие, называемое «спин-орбитальным», не учитывалось – потенциальная составляющая гамильтониана соответствовала простому кулоновскому притяжению электрических зарядов.
Спин-орбитальное взаимодействие вносит небольшие добавки в энергии состояний, снимающие вырождение многих из них. Следствием является появление «тонкой структуры» оптических спектров – то, что многие спектральные линии представляют собой дублеты, триплеты и т.д.

состояния. Энергии состояний зависят от квантовых чисел n и j)

отбора», выделяющих среди пар стационарных состояний атомов такие, между которыми

возможны переходы с излучением или поглощением фотонов. (О таких правилах говорилось еще применительно к модели Бора-Зоммерфельда.)
Одно из таких правил: орбитальные квантовые числа начального и конечного состояний радиационного перехода l1 и l2 должны удовлетворять условию
l =l1 – l2 = 1 .
Это правило можно рассматривать как отражающее закон сохранения момента импульса. Фотон обладает спином s=1 и при излучении «уносит» ненулевой момент импульса, в подавляющем большинстве случаев ħ. Поэтому «запрещенным» (маловероятным), например, оказывается переход 2s1s между двумя состояниями с l=0.

На следующем слайде приведены примеры анализа тонкой структуры некоторых линий спектра испускания водорода, учитывающий правила отбора.

энергии состояний с равными n и j (даже при разных

l) одинаковы.

сложным, чем атом водорода. В частности, к многоэлектронным атомам.
Экспериментальные данные

свидетельствуют, что спектры состояний многоэлектронных атомов дискретны. Об этом говорит, в частности, линейчатый характер оптических спектров многоэлектронных атомов и результаты изучения атомных столкновений (опыт Франка-Герца и последующие опыты).
В первом приближении (в пренебрежении спин-орбитальным взаимодействием) нейтральный атом можно представить системой из Z электронов (масса m, заряд –e) и ядра с зарядом Ze, взаимодействующих посредством кулоновских сил.
Волновая функция (пространственная часть) представляется зависящей от координат всех электронов:

Гамильтониан такой системы будет иметь вид:
, где

k – лапласиан для k-того электрона, в декартовых координатах имеющий вид

.
Однако даже в данном приближении это уравнение не

имеет аналитических решений. (Решения заведомо существуют, но не могут быть выражены через аналитические функции.) Поэтому используются способы приближенного, в том числе, численного решения.
Результаты теоретического исследования многоэлектронных систем потребовали введения (постулирования) некоторых дополнительных принципов и представлений.
Одно из них – представление о тождественности микрочастиц.

Все электроны обладают одинаковыми параметрами: массой, зарядом и спином. В классической физике частицы можно различить, отслеживая их траектории. Однако для микрообъектов (электронов), входящих в состав квантовых систем, этого не позволяет сделать принцип неопределенности.



неразличимыми. Признание этого накладывает дополнительные требования на вид волновых функций

квантовых систем
.
Они должны обладать свойством некоторой симметрии по отношению к перестановкам аргументов .
Математически доказывается, что это требование в конечном итоге приводит к результату, известному как принцип запрета Паули или просто принцип Паули:
«В системе тождественных фермионов все частицы должны находиться в различных состояниях.»
Заметим: бозоны (частицы с целым спиновым числом) не должны подчиняться этому принципу.

Принцип запрета был предложен Паули в 1925 г., еще до создания волновой механики. Как и постулаты Бора, его можно считать базовым постулатом, отражающим совокупность экспериментальных данных. В последующие теории эти постулаты входят в ином качестве – как следствия их собственных базовых положений. Таким образом работает принцип соответствия.
В описании многоэлектронных атомов принцип Паули играет важнейшую роль.

метод Хартри-Фока ( или метод самосогласованного поля).
Общую волновую функцию

системы
представляют через волновые функции , каждая из которых описывает состояние отдельного (k-того) электрона поле, создаваемом совместно ядром и остальными (Z–1) электронами, пребывающими в других (в соответствии с
принципом Паули) состояниях. Поле электронов характеризуется эффективным
потенциалом , волновая функция получается решением уравнения
Шредингера

с гамильтонианом

.

Полная энергия состояния атома получается суммированием энергий одноэлектронных состояний Ek .

для k-того электрона требуется

знание волновых функций остальных электронов, которые еще только должны быть определены в рамках той же процедуры.
Хартри предложил решать эту проблему методом последовательных приближений. В качестве исходных берутся, например, волновые функции состояний водородоподобного иона с зарядом ядра Z, по ним рассчитываются эффективные поля для одноэлектронных состояний, одноэлектронные волновые функции получаются решением уравнений Шредингера с соответствующими гамильтонианами, по ним уточняются эффективные поля, и т.д.
В дальнейшем метод Хартри был усовершенствован.
С его помощью были рассчитаны одноэлектронные волновые функции для основных состояний атомов всех химических элементов, а также для многих возбужденных состояний атомов и ионов. По полученным численным данным были построены аналитические аппроксимации.
Таким образом, задачу определения одноэлектронных волновых функций многоэлектронных атомов и соответствующих им энергий состояний можно считать решенной – благодаря конечности числа химических элементов.

и выделение стационарного состояния отдельного электрона в системе тождественных взаимодействующих

частиц является приближением – как и приписывание одноэлектронному состоянию определенных значений квантовых чисел и наблюдаемых величин.
Тем не менее, описанный метод позволил получить значения наблюдаемых величин (например, положения спектральных линий), подтверждаемых экспериментом. Поэтому его использование оправдано.
Вводится упрощенная классификация одноэлектронных состояний (определенных без учета спин-орбитального взаимодействия), основанная на значениях
приписываемых им квантовых чисел n, l, m и mS (проекция спина).
Энергии одноэлектронных состояний, определенные методом Хартри-Фока, зависят лишь от квантовых чисел n и l, причем зависимость от главного квантового числа n – более резкая.
Вводятся определения электронной оболочки и электронного слоя, основанные на значениях энергии одноэлектронных состояний (а не на каких-либо параметрах пространственных распределений).
Набор состояний электронов с фиксированными значениями квантовых чисел n и l называется электронной оболочкой.
Энергии состояний одной электронной оболочки равны (в пределах используемого приближения, не учитывающего спин-орбитального взаимодействия).

m (целые числа от –l до l) и ms (–1/2

и 1/2). Оно не зависит от n равно 2(2l+1).
Обозначения оболочек и числа состояний приведены в таблице:




Набор состояний с фиксированным значением главного квантового числа n называется электронным слоем. Число электронных оболочек в электронном слое
определяется диапазоном изменения l (целые числа от 0 до n–1) и равно n.
Число состояний в слое равно 2n2.
Обозначения слоев и числа состояний приведены в таблице:



Примеры:
K-слой содержит единственную электронную оболочку 1s;
M-слой содержит электронные оболочки 3s, 3p и 3d.

не более одного электрона. Иными словами, состояние может быть либо

заполненным, либо вакантным (пустым).
Электронная конфигурация – распределение электронов по электронным оболочкам, то есть, по состояниям с различными значениями n и l.
Энергия атома EA в рамках данного приближения (где состояния с равными n и l вырождены) получается суммированием энергий заполненных одноэлектронных состояний Enl:
,
где qnl – число заполненных состояний в оболочке nl.
Основное состояние атома характеризуется наименьшей энергией. В основном состоянии заполнены одноэлектронные состояния с наименьшими энергиями.

Описанные закономерности основаны на приближенном описании состояний многоэлектронных атомов, однако в общих чертах соответствуют опытным данным.
В частности, n-ный период в таблице Менделеева содержит 2n2 элементов; атомам инертных газов в основном состоянии соответствуют электронные конфигурации с
полностью заполненными электронными слоями.
Более детальные закономерности выявляются при использовании более корректных и сложных моделей, разработанных в рамках квантовой механики.