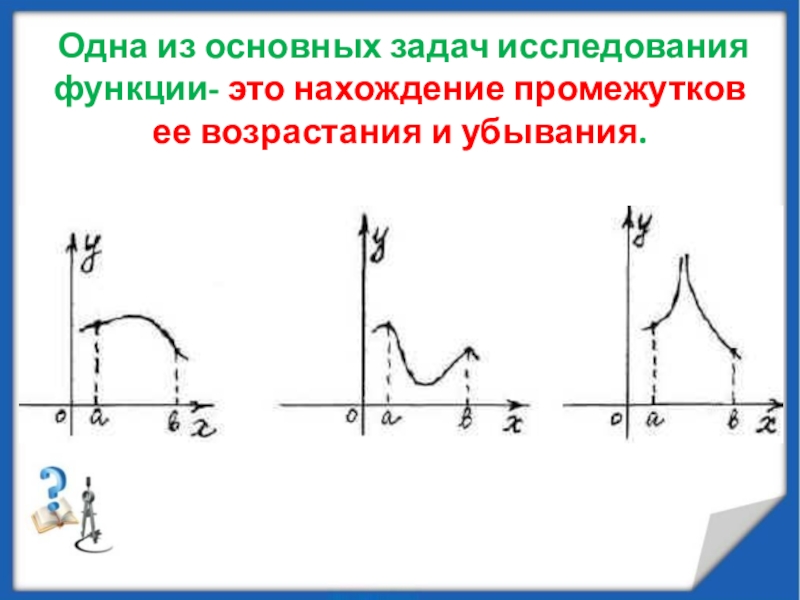
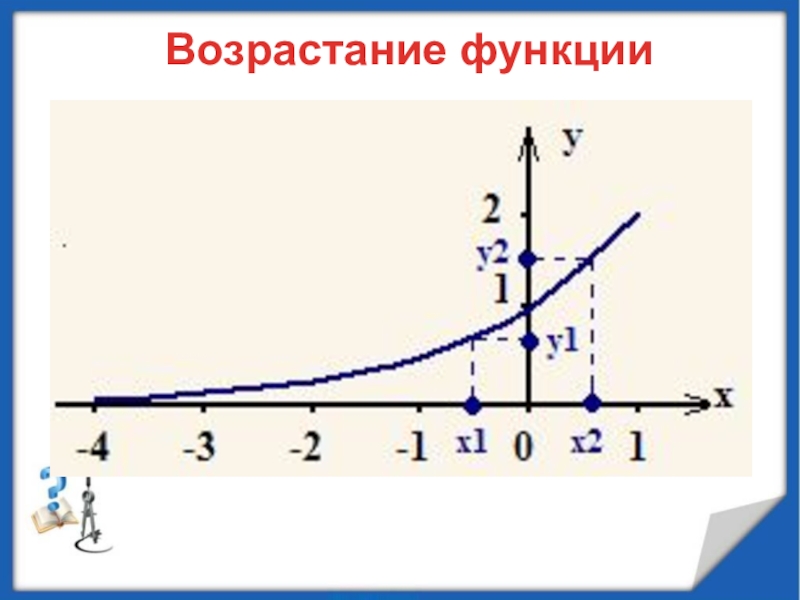
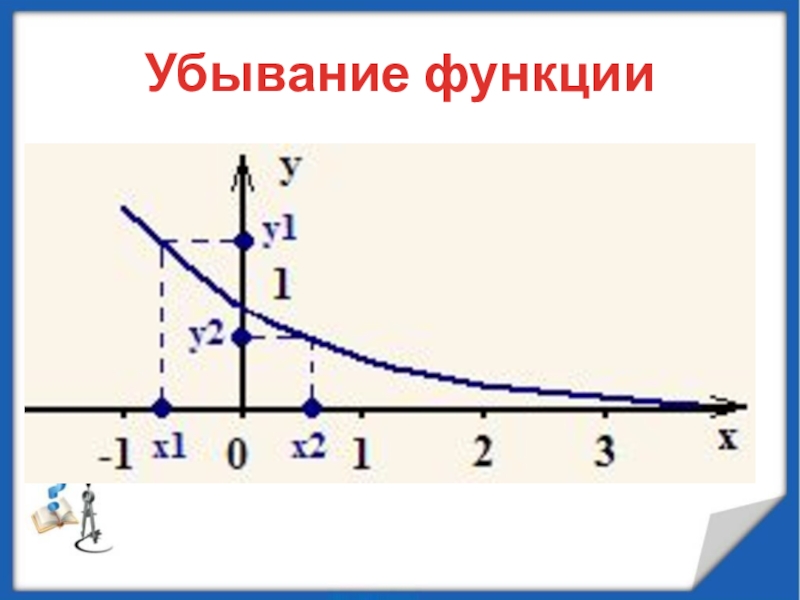
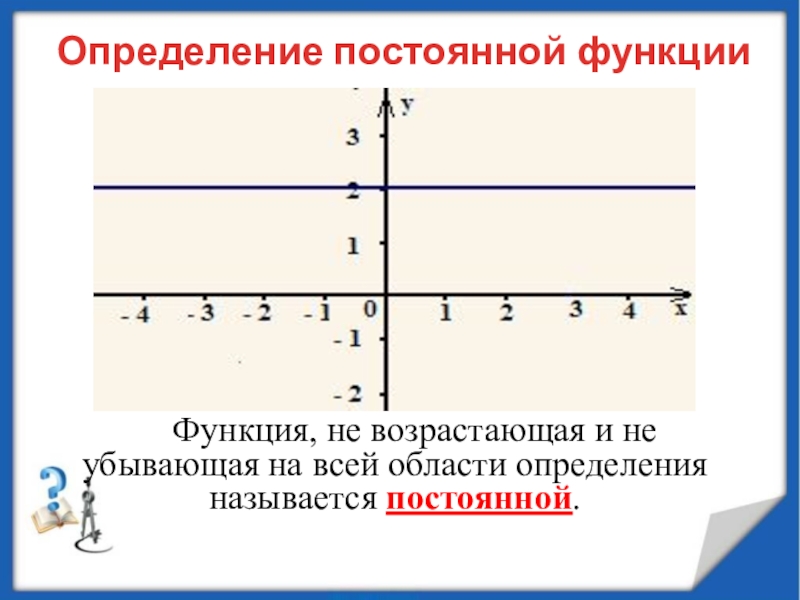
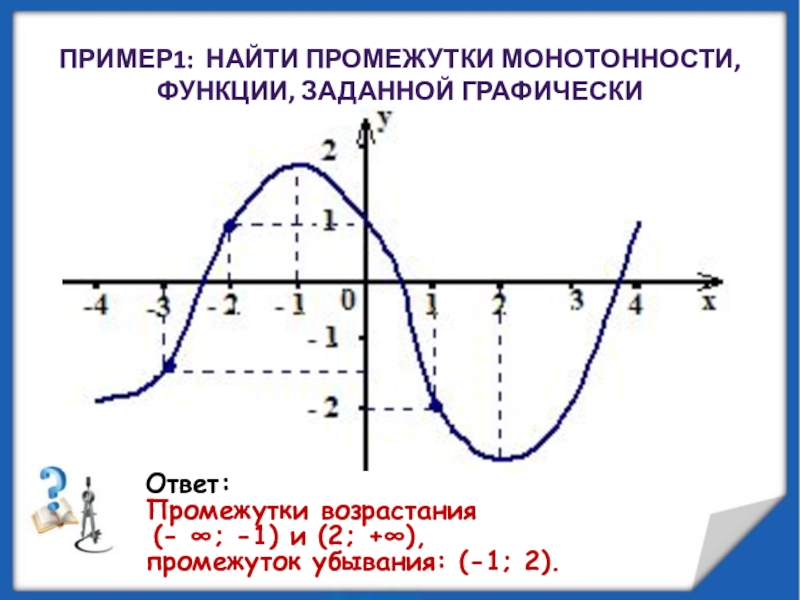
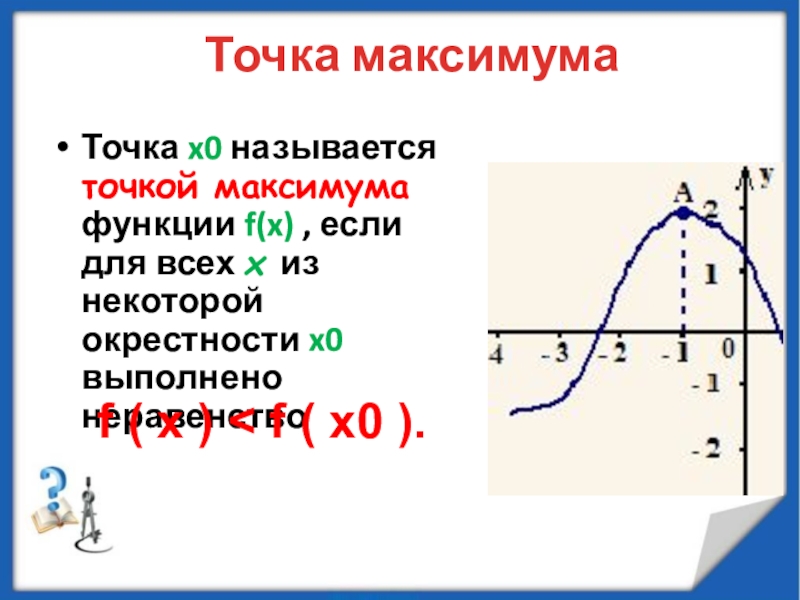
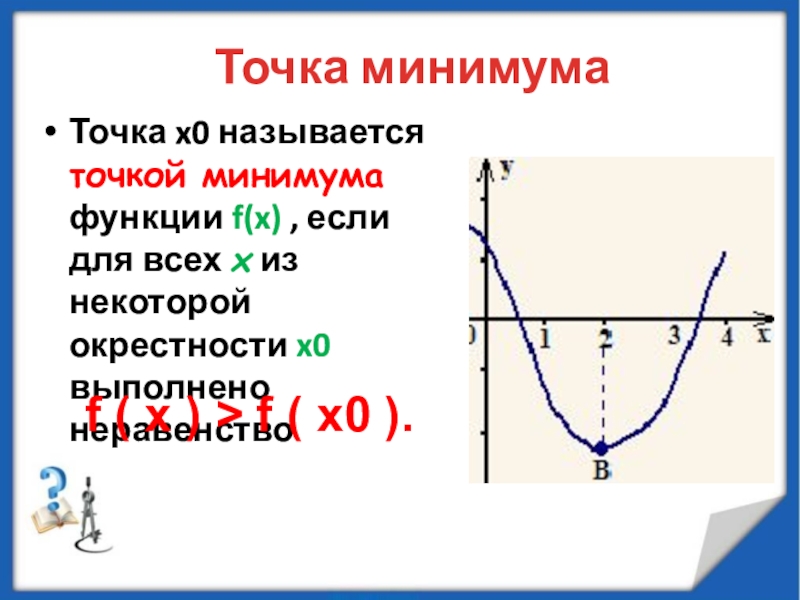
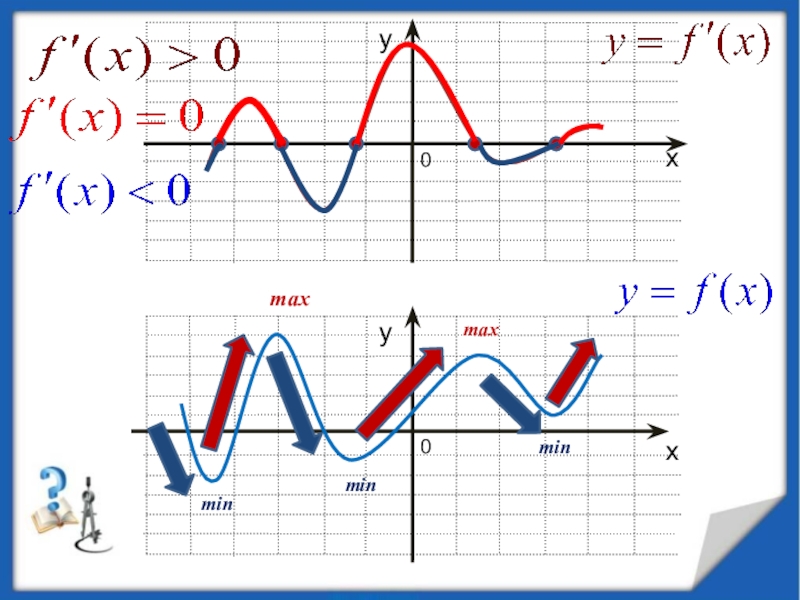
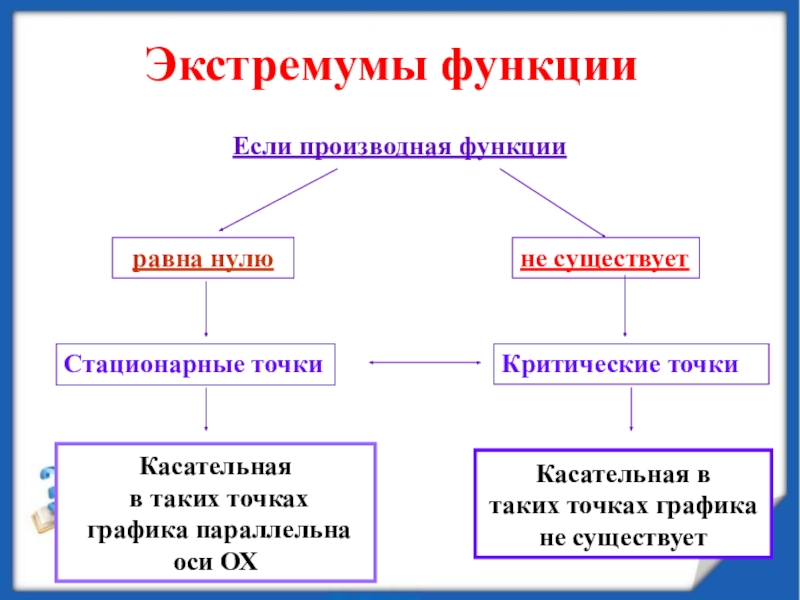
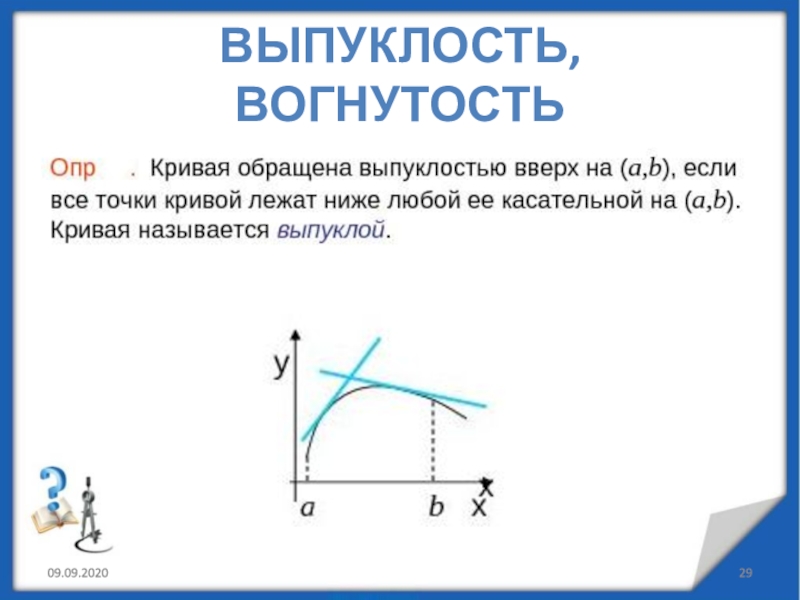
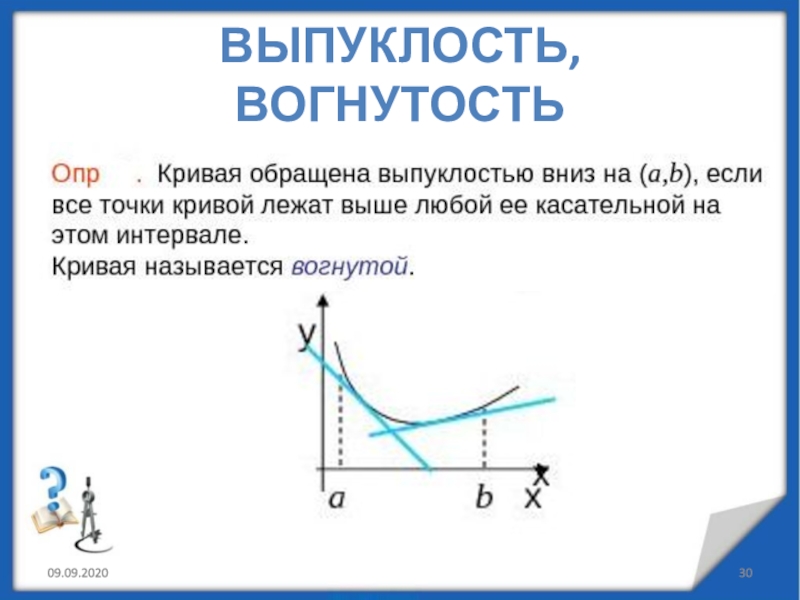
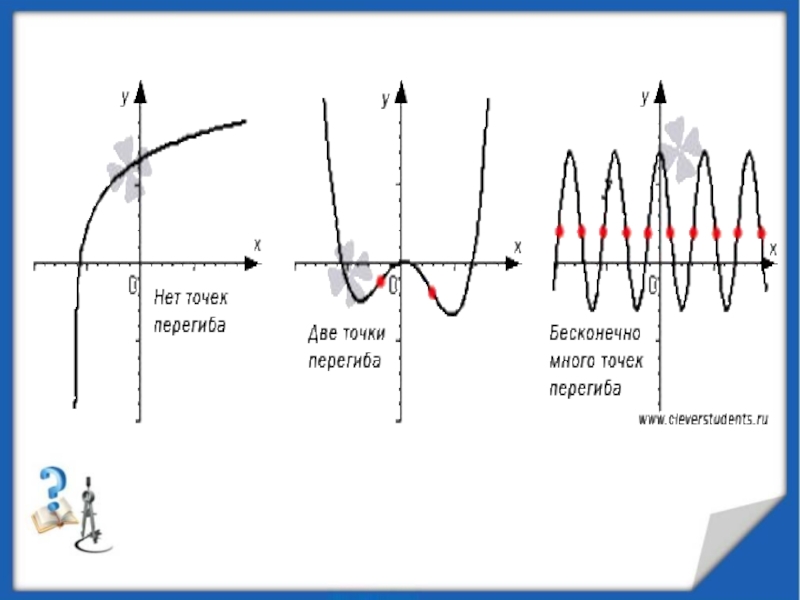
минимумы.
Правило нахождения интервалов монотонности и экстремумы. Исследование функции на монотонность
и экстремум.Отыскание наибольших и наименьших значений функций. Задачи на отыскание наибольших и наименьших значений величин.
Основные вопросы: