Слайд 1Кафедра общественного здоровья и здравоохранения
По дисциплине «Доказательная медицина»
Тема: Этапы статистического
исследования.
лекция № 6 для студентов 1 курса, обучающихся по специальности
060101 -– «Лечебное дело»
Зав. кафедрой ОЗиЗ
К.м.н. доц. Шульмин А. В.
Красноярск, 2011
Слайд 2Цель лекции
Ознакомление с основными этапами статистического исследования
Слайд 3План лекции:
I. Формирование цели и задач исследования.
II. Организация исследования.
III. Сбор
информации.
IV. Обработка информации.
V. Анализ результатов исследования.
VI. Внедрение результатов исследования в
практику и оценка эффективности внедрения.
Слайд 4Формирование цели и задач исследования
Цель - отвечает на вопрос зачем
проводится данное исследование.
Задачи исследования - дают ответ на вопрос как
будет достигнута цель.
Слайд 6Цель любого исследования доказательство чего либо
Доказывать можно как наличие, так
и отсутствие факта (воздействие препарата и т. д.).
Доказанное отсутствие результата
это тоже результат!
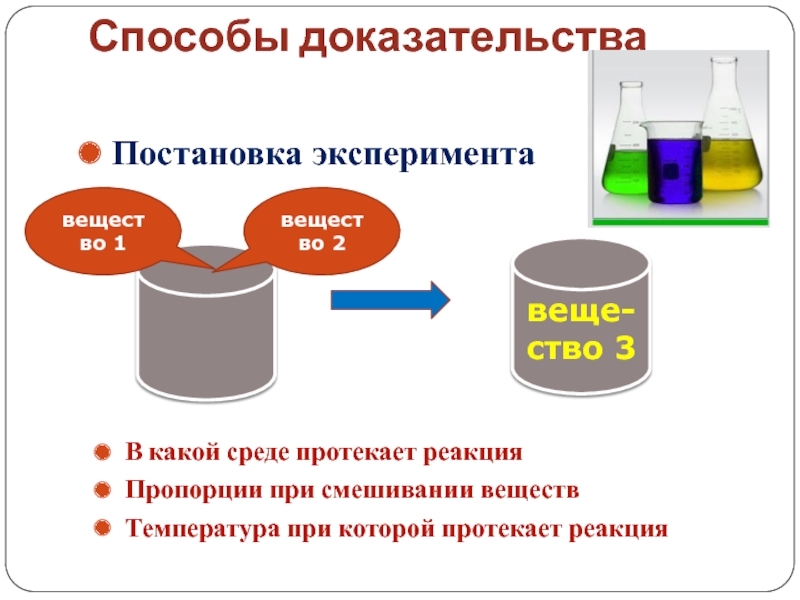
Слайд 7Способы доказательства
Постановка эксперимента
вещество 1
вещество 2
веще-ство 3
В какой среде протекает
реакция
Пропорции при смешивании веществ
Температура при которой протекает реакция
Слайд 8Френк Йейтс (1937)
«Большинству биологических объектов свойственна вариабельность, и прелесть
простоты и воспроизводимости физических и химических экспериментов утрачивается. А значит,
на передний план выдвигаются статистические проблемы»
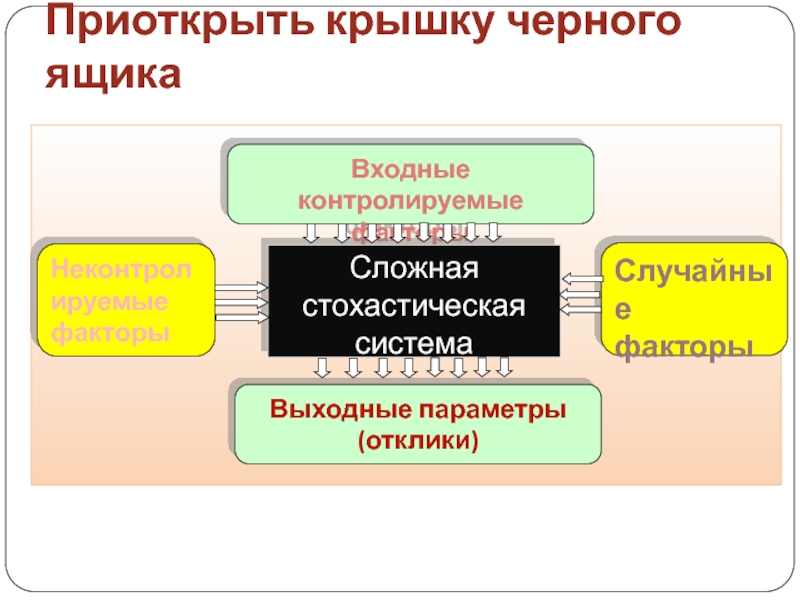
Слайд 10Что нужно для доказательства?
Что бы доказать математическую теорему: интеллект, чистые
листы бумаги и ручка;
Что бы доказать наличие химических или физических
реакций: интеллект, инструментарий, реагенты и приборы фиксирующие результаты;
Что бы ДОКАЗАТЬ ВОЗДЕЙСТВИЕ ФАКТОРА или группы факторов НА БИОЛОГИЧЕСКИЙ ОБЪЕКТ: интеллект, инструментарий, реагенты и приборы фиксирующие результаты и НАУКА СТАТИСТИКА
Слайд 11Для чего нужно конкретное исследование?
Наука
Наука
Наука
Наука
Практика
Слайд 12Организация исследования:
План исследования предусматривает методику проведения исследования, дает раскладку организационных
вопросов (что, где, когда, сколько?).
Определяет субъектов исследования.
Слайд 13Организация исследования:
Программа исследования(отвечает на вопрос как делать) состоит из трех
главных компонентов :
программы сбора материала;
программы его разработки (табличной
сводки);
программы анализа.
Прежде всего устанавливается объект исследования и единица наблюдения.
Слайд 14Организация исследования:
Под объектом наблюдения понимают статистическую совокупность, состоящую из отдельных
предметов или явлений - единиц наблюдений, взятых в определённых границах
времени и пространства.
Единица наблюдения - первичный элемент статистической совокупности, являющейся носителем признаков, подлежащих регистрации, изучению в ходе исследования.
Учетные признаки – признаки подлежащие регистрации в ходе статистического исследования.
Слайд 21Вопрос №1 Где это будет работать.
Эксперимент в условиях клинической базы
Внедрение
в работу практического врача участковой больницы
или
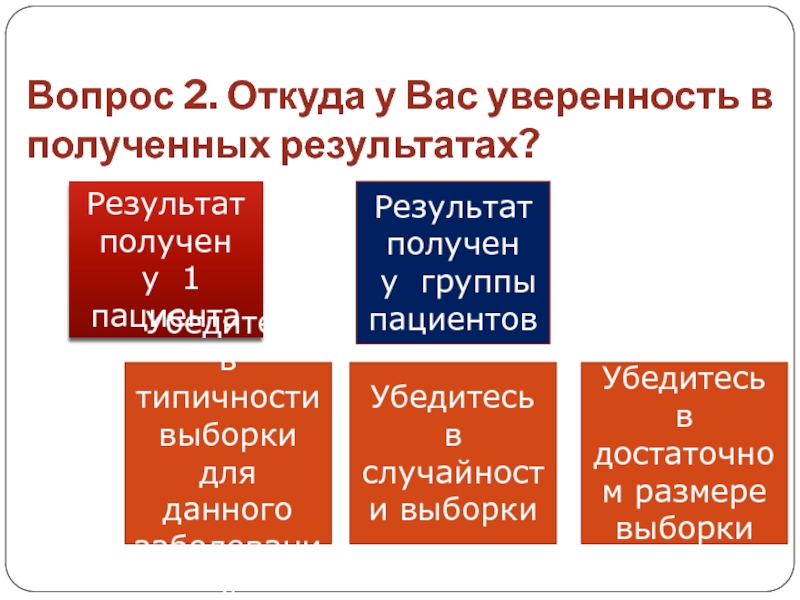
Слайд 23Вопрос 2. Откуда у Вас уверенность в полученных результатах?
Результат получен
у 1
пациента
Результат получен
у группы
пациентов
Убедитесь в типичности выборки
для данного заболевания
Убедитесь в случайности выборки
Убедитесь в достаточном размере выборки
Слайд 24Вопрос 3. Почему Вам должны верить?
Результат получен
у группы
пациентов
Докажите
типичность выборки для данного заболевания
Докажите случайность формирования выборки
Докажите достаточный размер
выборки
Слайд 25Пример нерепрезентативной выборки
В США одним из наиболее известных исторических примеров
нерепрезентативной выборки считается случай, происшедший во время президентских выборов в
1936 году[1]. Журнал «Литрери Дайджест», успешно прогнозировавший события нескольких предшествующих выборов, ошибся в своих предсказаниях, разослав десять миллионов пробных бюллетеней своим подписчикам, а также людям, выбранным по телефонным книгам всей страны и людям из регистрационных списков автомобилей. В 25 % вернувшихся бюллетеней (почти 2,5 миллиона) голоса были распределены следующим образом:
57 % отдавали предпочтение кандидату-республиканцу Альфу Лэндону 40 % выбрали действующего в то время президента-демократа Франклина Рузвельта
На действительных же выборах, как известно, победил Рузвельт, набрав более 60 % голосов. Ошибка «Литрери Дайджест» заключалась в следующем: желая увеличить репрезентативность выборки, — так как им было известно, что большинство их подписчиков считают себя республиканцами, — они расширили выборку за счёт людей, выбранных из телефонных книг и регистрационных списков. Однако они не учли современных им реалий и в действительности набрали ещё больше республиканцев: во время Великой депрессии обладать телефонами и автомобилями могли себе позволить в основном представители среднего и высшего класса (то есть большинство республиканцев, а не демократов).

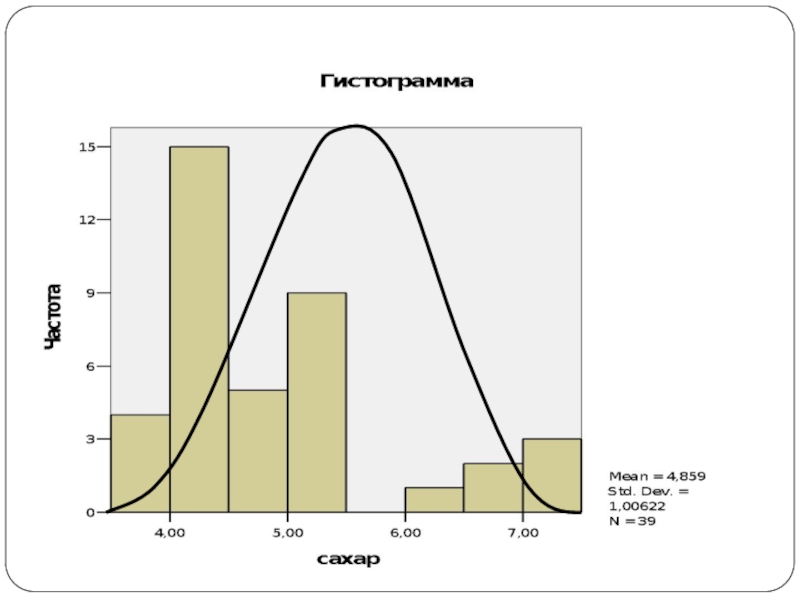
Слайд 26Распространенное выражение
Уровень сахара в крови у исследуемой группы составил 4,9±1,0(δ)
ммоль/л.
Слайд 28Медиана и процентили
Уровень сахара в крови у исследуемой группы составил
4,3 [3,7;6,2] ммоль/л (Ме [P10;P90]).
Слайд 29Sample saze
Andrey Rodionov MD, MPH
Исследования сплошные и выборочные
Что такое сплошные
и выборочные исследования?
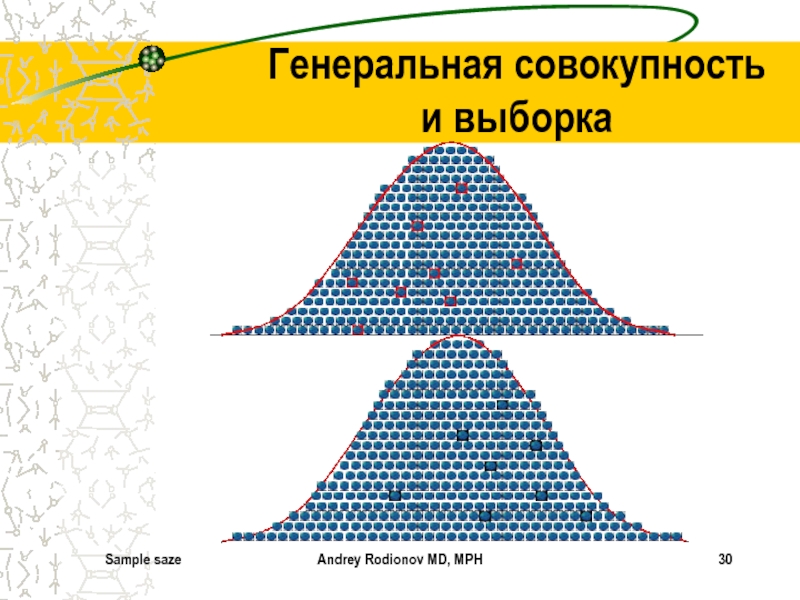
Понятие о генеральной совокупности
Все субъекты, подходящие для проведения
исследования
Самая большая генеральная совокупность – все человечество
Методы аналитической статистики при исследовании генеральной совокупности не применяются
Понятие выборки
Слайд 30Sample saze
Andrey Rodionov MD, MPH
Генеральная совокупность и выборка
Слайд 31Sample saze
Andrey Rodionov MD, MPH
Допущение
Результаты, полученные на
выборке можно распространить на всю генеральную
совокупность (с известным допущением, выражаемым через вероятности ά- и β-ошибок)
Слайд 32Sample saze
Andrey Rodionov MD, MPH
Почему исследователи любят выборочные исследования
Меньше работы
Меньше
денег
Меньше времени
Меньше головной боли (?)
Слайд 33Sample saze
Andrey Rodionov MD, MPH
Оптимальный размер выборки
В интересах исследователя
В интересах
реально существующей ситуации в генеральной совокупности
Слайд 34Sample saze
Andrey Rodionov MD, MPH
Вопросы, предваряющие процедуру выборки
Как сделать репрезентативную
выборку?
или
Как избежать ошибки отбора selection bias
и
Насколько я готов ошибиться исходя
из того, что обследована будет не генеральная совокупность а выборка из нее?
Слайд 35Sample saze
Andrey Rodionov MD, MPH
Способы формирования выборки. Понятие о рандомизации
Выборки
не основанные на вероятностях non-probability samples
Выборки вероятностные probability samples
Рандомизация randomization
Слайд 36Sample saze
Andrey Rodionov MD, MPH
Виды выборки не основанной на вероятностях
Простая
случайная simple random sample
Систематическая выборка systematic sample
Удобная выборка sample of
convenience
Слайд 37Простая вероятностная выборка:
Простая повторная выборка. Использование такой выборки основывается
на предположении, что каждый респондент с равной долей вероятности может
попасть в выборку. На основе списка генеральной совокупности составляются карточки с номерами респондентов. Они помещаются в колоду, перемешиваются и из них наугад вынимается карточка, записывается номер, потом возвращается обратно. Далее процедура повторяется столько раз, какой объём выборки нам необходим. Минус: повторение единиц отбора.
Sample saze
Andrey Rodionov MD, MPH
Слайд 38Систематическая вероятностная выборка.
Sample saze
Andrey Rodionov MD, MPH
Является упрощенным вариантом
простой вероятностной выборки. На основе списка генеральной совокупности через определённый
интервал (К) отбираются респонденты. Величина К определяется случайно. Наиболее достоверный результат достигается при однородной генеральной совокупности, иначе возможны совпадение величины шага и каких-то внутренних циклических закономерностей выборки (смешение выборки). Минусы: такие же как и в простой вероятностной выборке.
Слайд 39«Удобная» выборка.
Процедура «удобной» выборки состоит в установлении контактов с
«удобными» единицами выборки — с группой студентов, спортивной командой, с друзьями
и соседями. Если необходимо получить информацию о реакции людей на новую концепцию, такая выборка вполне обоснована. «Удобную» выборку часто используют для предварительного тестирования анкет.
Sample saze
Andrey Rodionov MD, MPH
Слайд 40Sample saze
Andrey Rodionov MD, MPH
Виды вероятностной выборки
Кластерная выборка cluster sample
Стратифицированная
выборка stratified sample
Зонная выборка zone sample
Многоэтапная выборка multilevel sample
Слайд 41Серийная (гнездовая, кластерная) выборка.
Единицы отбора представляют собой статистические серии (семья,
школа, бригада и т. п.). Отобранные элементы подвергаются сплошному обследованию. Отбор статистических
единиц может быть организован по типу случайной или систематической выборки. Минус: Возможность большей однородности, чем в генеральной совокупности.
Sample saze
Andrey Rodionov MD, MPH
Слайд 42Sample saze
Andrey Rodionov MD, MPH
Простая случайная выборка
Жребий (к/ф «Гараж»)
Кубики
Генератор случайных
чисел
Программа PEPI
Слайд 43Sample saze
Andrey Rodionov MD, MPH
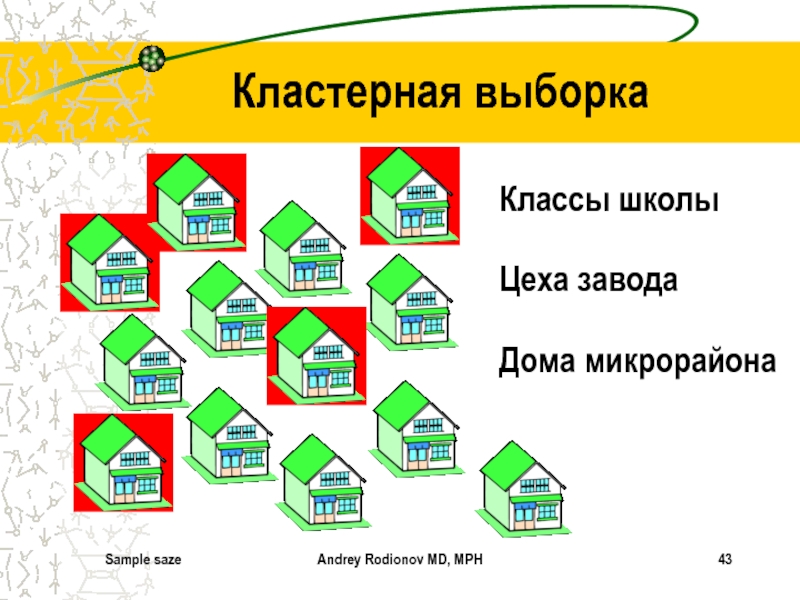
Кластерная выборка
Классы школы
Цеха завода
Дома микрорайона
Слайд 44Sample saze
Andrey Rodionov MD, MPH
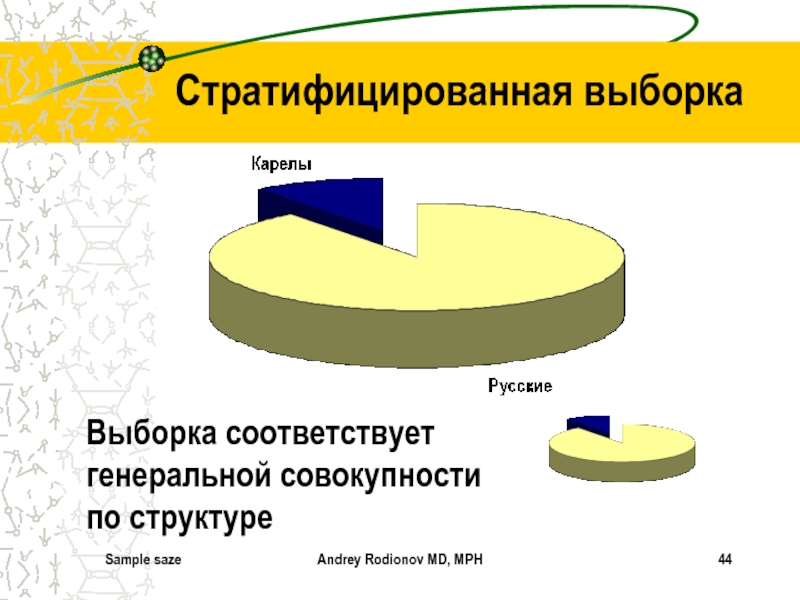
Стратифицированная выборка
Выборка соответствует генеральной совокупности по
структуре
Слайд 45Sample saze
Andrey Rodionov MD, MPH
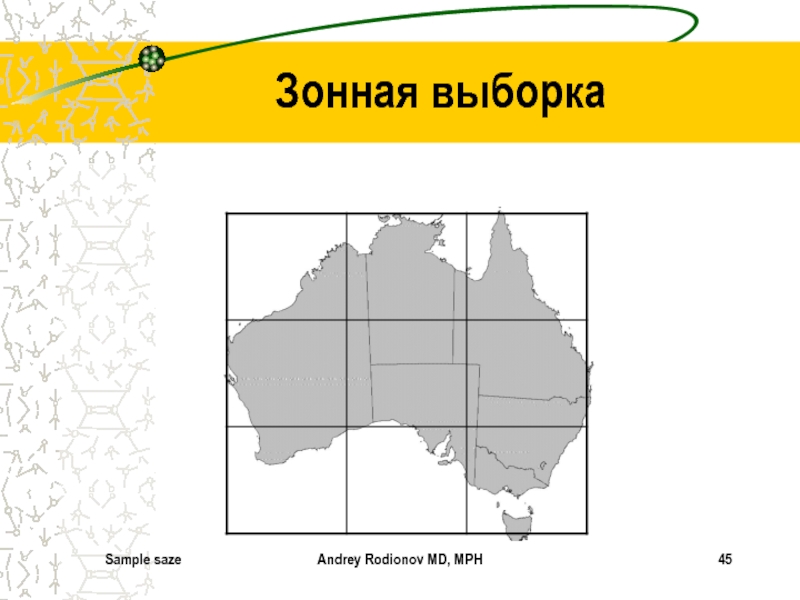
Зонная выборка
Слайд 46Sample saze
Andrey Rodionov MD, MPH
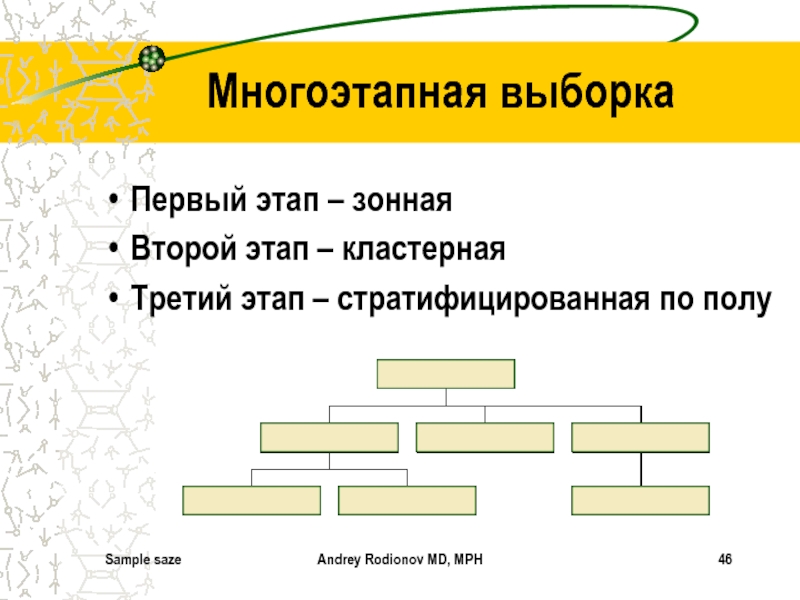
Многоэтапная выборка
Первый этап – зонная
Второй этап
– кластерная
Третий этап – стратифицированная по полу
Слайд 47Sample saze
Andrey Rodionov MD, MPH
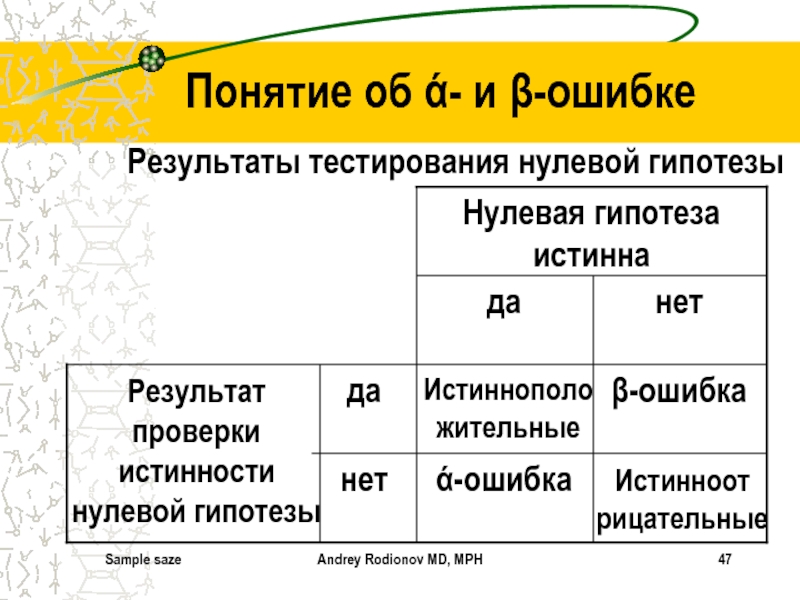
Понятие об ά- и β-ошибке
Результаты тестирования
нулевой гипотезы
Истинноот рицательные
ά-ошибка
нет
β-ошибка
Истинноположительные
да
Результат проверки истинности нулевой гипотезы
нет
да
Нулевая гипотеза истинна
Слайд 48Sample saze
Andrey Rodionov MD, MPH
ά- и β-ошибки в выборочном исследовании
Вероятность
ошибки – P value, величина p.
Какую величину p мы можем
допустить?
pά <0.05
pβ <0.2 (0.1)
Что такое pά <0.05 pβ <0.2
0.05 0.2
5% 20%
1/20 1/5
Слайд 49Sample saze
Andrey Rodionov MD, MPH
Величина pά для выборки
Величина p
говорит о том, что я готов найти различия по какому-нибудь
параметру менее чем в 5% выборок одинаковой численности, формируя их одну за другой случайным образом из генеральной совокупности, или что меньше чем одна выборка из двадцати не будет адекватно представлять по этому параметру генеральную совокупность или более чем 95% (более чем 19 из 20) всех таких выборок будут адекватно представлять генеральную совокупность.
Слайд 50Sample saze
Andrey Rodionov MD, MPH
Размер выборки
От чего зависит минимальный допустимый
размер выборки?
Слайд 51Sample saze
Andrey Rodionov MD, MPH
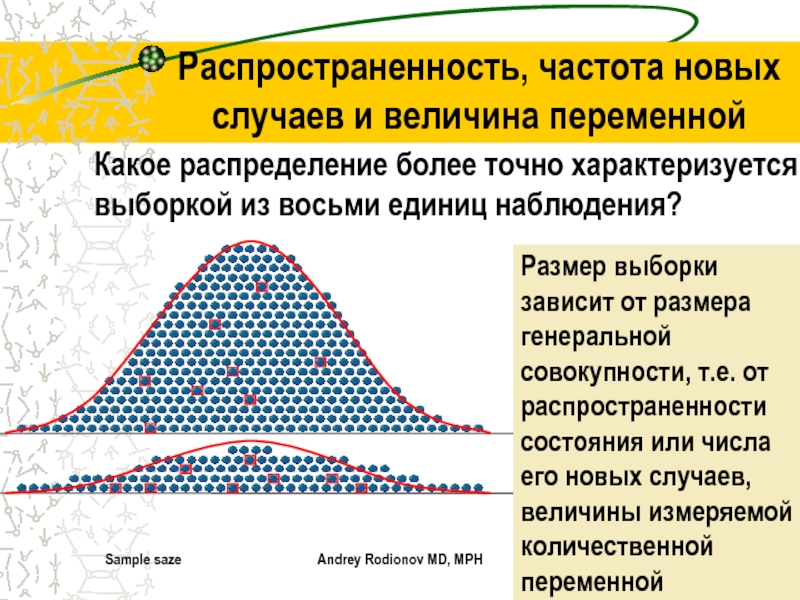
Распространенность, частота новых случаев и величина
переменной
Какое распределение более точно характеризуется выборкой из восьми единиц наблюдения?
Размер
выборки зависит от размера генеральной совокупности, т.е. от распространенности состояния или числа его новых случаев, величины измеряемой количественной переменной
Слайд 52Sample saze
Andrey Rodionov MD, MPH
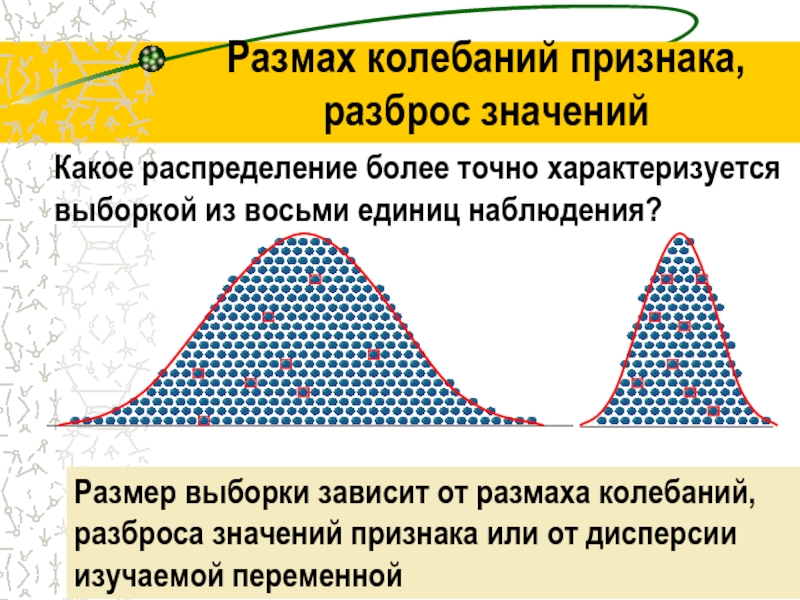
Размах колебаний признака,
разброс значений
Какое распределение более точно характеризуется
выборкой из восьми единиц наблюдения?
Размер выборки зависит от размаха колебаний, разброса значений признака или от дисперсии изучаемой переменной
Слайд 53Sample saze
Andrey Rodionov MD, MPH
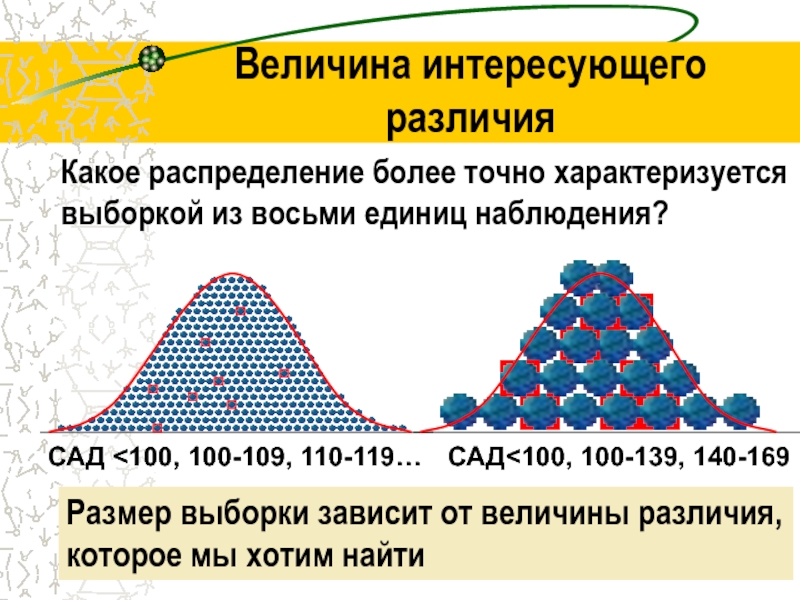
Величина интересующего различия
САД
100-139, 140-169
Какое распределение более точно характеризуется выборкой из восьми единиц
наблюдения?
Размер выборки зависит от величины различия, которое мы хотим найти
Слайд 54Sample saze
Andrey Rodionov MD, MPH
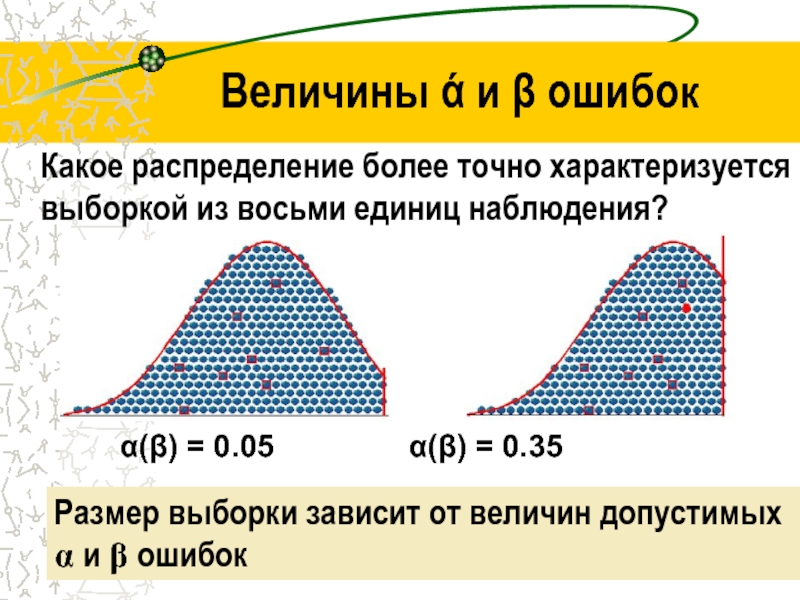
Величины ά и β ошибок
Какое распределение
более точно характеризуется выборкой из восьми единиц наблюдения?
Размер выборки зависит
от величин допустимых α и β ошибок
α(β) = 0.05 α(β) = 0.35
Слайд 55Sample saze
Andrey Rodionov MD, MPH
Обобщенная формула
РВ – минимальный размер выборки
Распр
– распространенность, частота новых случаев или величина изучаемой переменной
α и
β- ошибки – обычно 0.05 и 0.2(0.1) соответственно
МЗР – минимальное значимое различие, обнаружение которого нами запланировано
Для нормального распределения
Zά (для ά=0.05) = 1.96 Zβ (для β=0.2) = 0.84
Слайд 56Sample saze
Andrey Rodionov MD, MPH
Для парного t - теста
n –
количество пар
Sd – стандартное отклонение для n различий
D – минимальное
значимое различие
Zα – для α=5% = 1.96
Zβ – для β=20% = 0.84
Слайд 57Sample saze
Andrey Rodionov MD, MPH
Для двух независимых групп
n – размер
группы (при условии, что n=n1=n2
S – стандартное отклонение для n
различий
D – минимальное значимое различие
Zα – для α=5% = 1.96
Zβ – для β=20% = 0.84
Слайд 58Sample saze
Andrey Rodionov MD, MPH
Для сравнения пропорций
Настоящая формула очень сложная
Иногда
с практической и познавательной целью используют упрощенную формулу
Она дает чуть
меньшее значение n, чем должно быть в действительности и чуть большую вероятность β-ошибки
Слайд 59Sample saze
Andrey Rodionov MD, MPH
Для сравнения пропорций (2)
n – размер
групп 1 и 2, при условии, что n=n1=n2
p (доля1+доля2)/(группа1+группа2)
D –
минимально приемлемые различия
Zα = 1.96
Zβ = 0.84
Слайд 60Sample saze
Andrey Rodionov MD, MPH
Для оценки величины
n – размер группы
Zα
= 1.96
SD – стандартное отклонение для измеряемой величины
M – величина
измеряемой переменной
Слайд 61Sample saze
Andrey Rodionov MD, MPH
Вместо заключения
Откуда брать недостающие данные для
расчета минимального размера выборки
Литературные данные
Пилотное исследование
Используйте проверенные компьютерные программы (PEPI)
Доступна
бесплатная версия
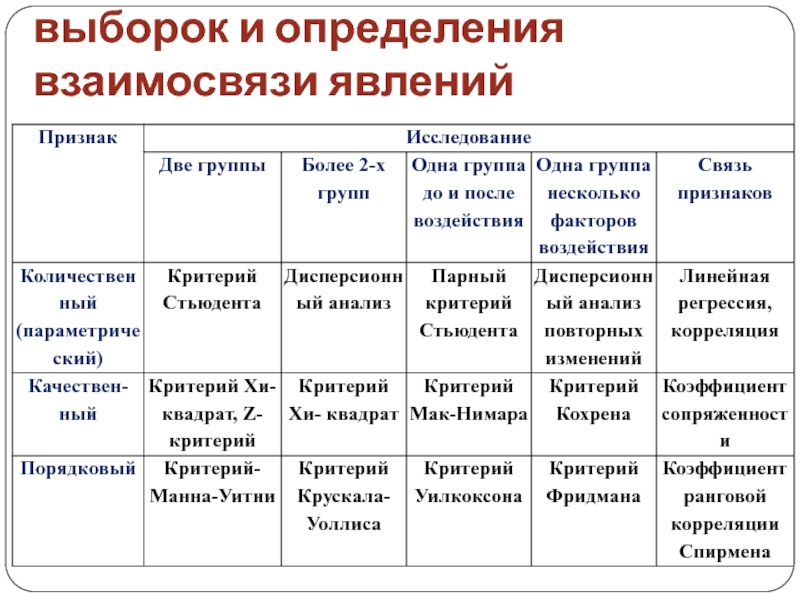
Слайд 63Выбор метода сравнения выборок и определения взаимосвязи явлений
Слайд 64Ограничение применения Z - критерия
При применении Z критерия или как
его иногда называют, критерия Стьюдента для долей, должно выполнятся правило
np и n(1 – p) больше 5 или 500 для %. Если хотя бы для одной выборки это условие не выполняется, то критерий z неприменим, и нужно воспользоваться точным критерием Фишера.
Пример выборка 20 человек соотношение признака 20% к 80%, 20*20=400<500
Слайд 65Ограничение применения критерия Хи-квадрат
Для критерия Хи-квадрат консервативное правило гласит, что
ни одно значение ожидаемой частоты в группе должно быть меньше
5, и общая выборка должна составлять, как минимум, 20 человек в противном случае нужно воспользоваться точным критерием Фишера.
Многие статистические пакеты учитывают этот принцип!!!
Слайд 66Факторный анализ
Общее правило для факторного анализа применять его не менее,
чем для 300 случаев, или, более мягкое правило, - не
менее, чем 50 испытуемых для каждого фактора. Comprey & Lee (1992) приводят такие указания касательно размера выборки в факторном анализе: 50 очень плохо, 100 плохо, 200 сойдет, 300 хорошо, 500 очень хорошо, 1000 отлично.
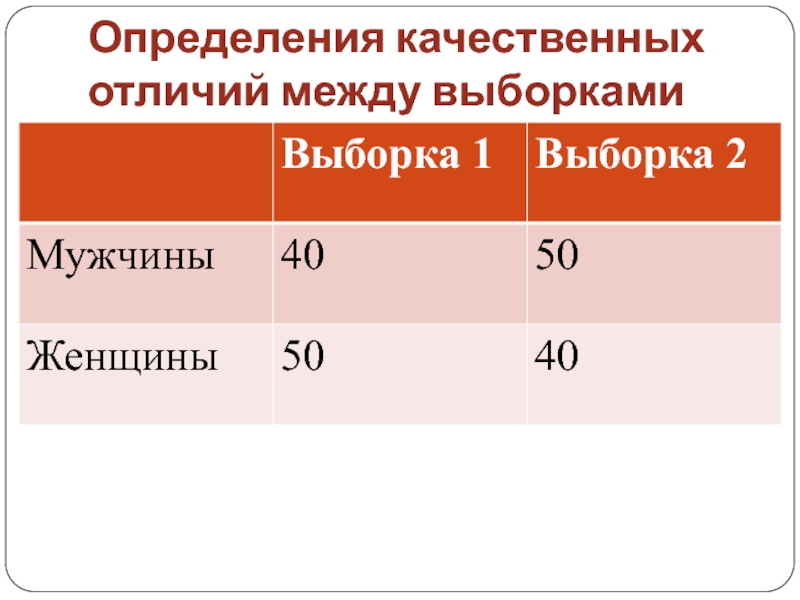
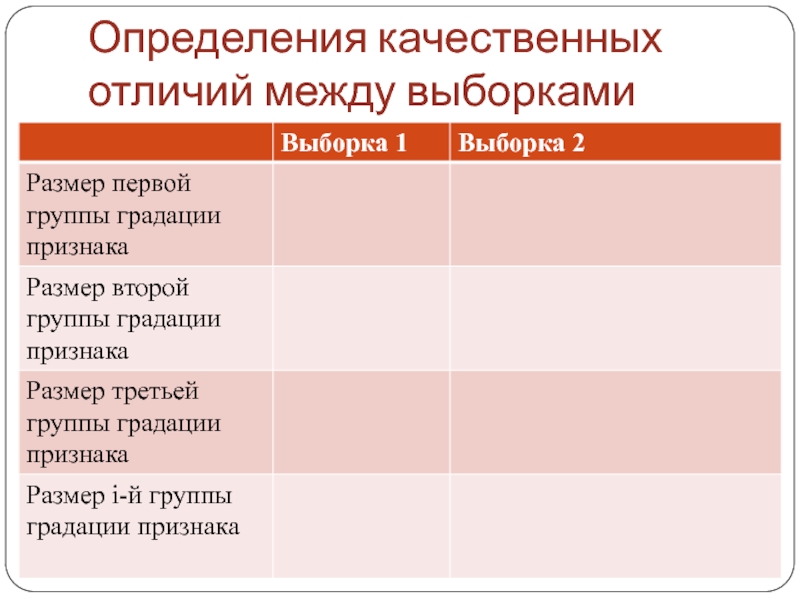
Слайд 67Определения качественных отличий между выборками
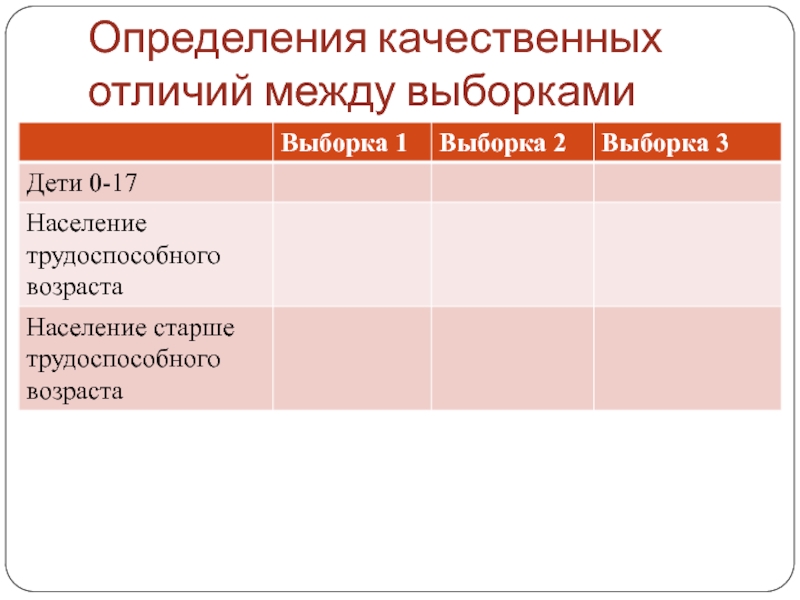
Слайд 68Определения качественных отличий между выборками
Слайд 69Определения качественных отличий между выборками
Слайд 70 “Для проверки в клинике имеются два пути, отнюдь не
исключающие друг друга и одинаково важные. Я разумею путь статистического
доказательства, с одной стороны, и точное клиническое наблюдение каждого отдельного случая — с другой”.
В. А. Манассеин
Слайд 71Выводы:
Таким образом мы рассмотрели:
Правила представления результатов исследования и оценка медицинских
публикаций
Слайд 72Рекомендованная литература по теме занятия:
- обязательная;
Павлушков И.В. Основы высшей
математики и математической статистики: Учебник для мед. вузов
- дополнительная;
1. А.
Петри, К. Сэбин Наглядная медицинская статистика. – М.: ГЭОТАР- Медиа, 2009. – С. 71-86.
2. Зайцев В. М., Лифляндский В. Г., Маринкин В. И. Прикладная медицинская статистика: Учебное пособие. - СПб.: Фолиант, 2006. – С. 262-286.




















![Кафедра общественного здоровья и здравоохранения
По дисциплине Доказательная Медиана и процентилиУровень сахара в крови у исследуемой группы составил 4,3 [3,7;6,2] ммоль/л (Ме [P10;P90]). Медиана и процентилиУровень сахара в крови у исследуемой группы составил 4,3 [3,7;6,2] ммоль/л (Ме [P10;P90]).](/img/thumbs/999c42082dd266b2d613302c4f413a88-800x.jpg)