Капиллярная конденсация

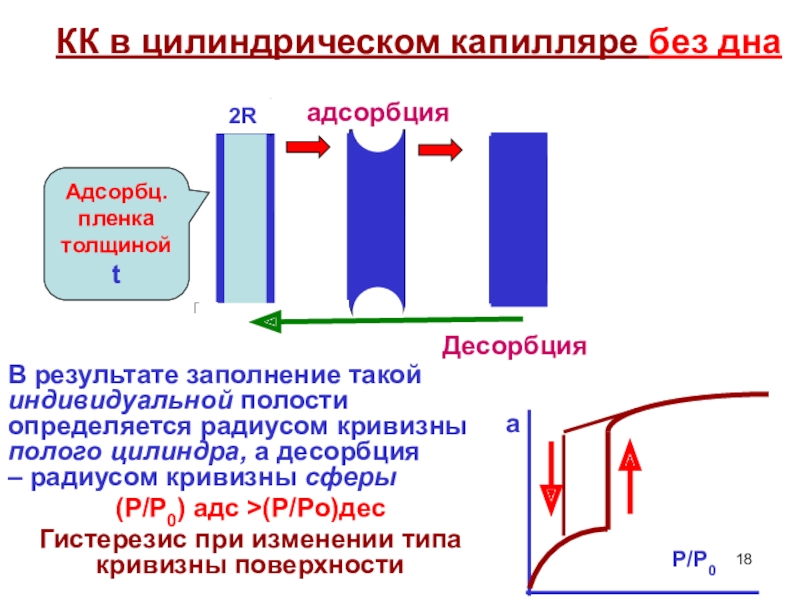
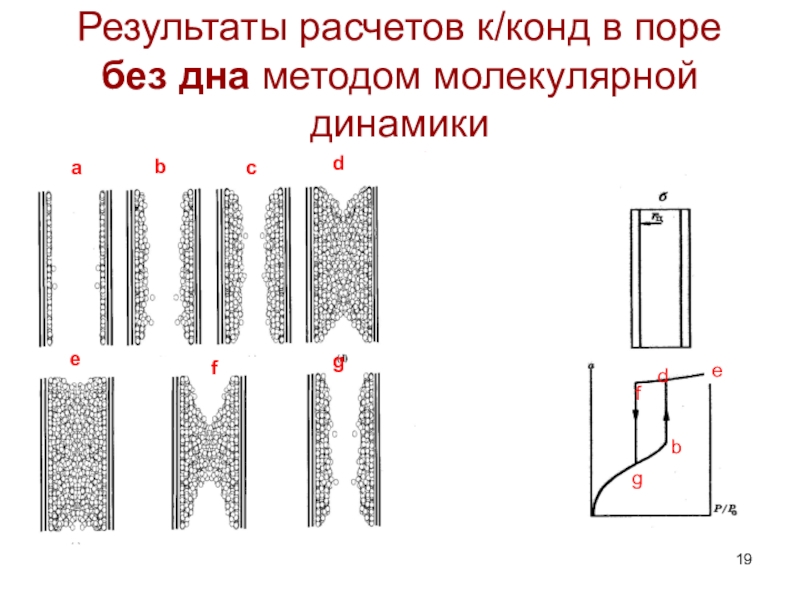
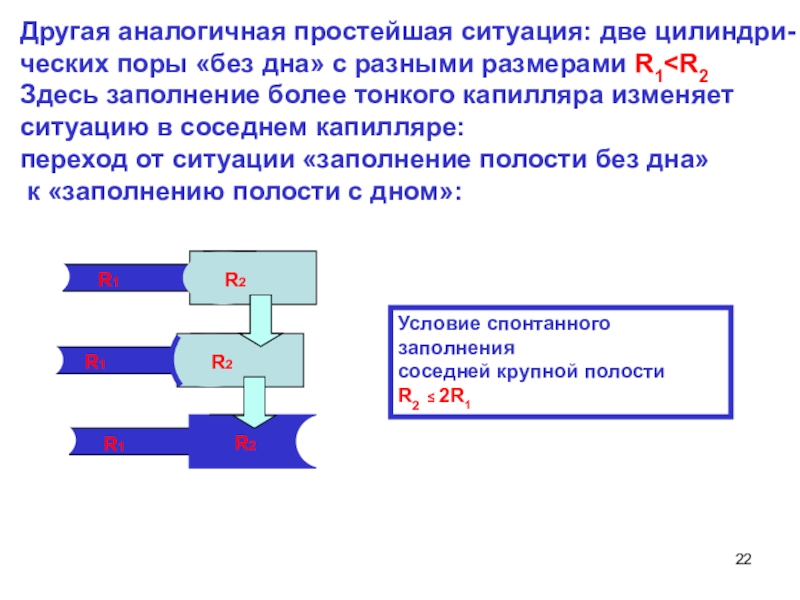
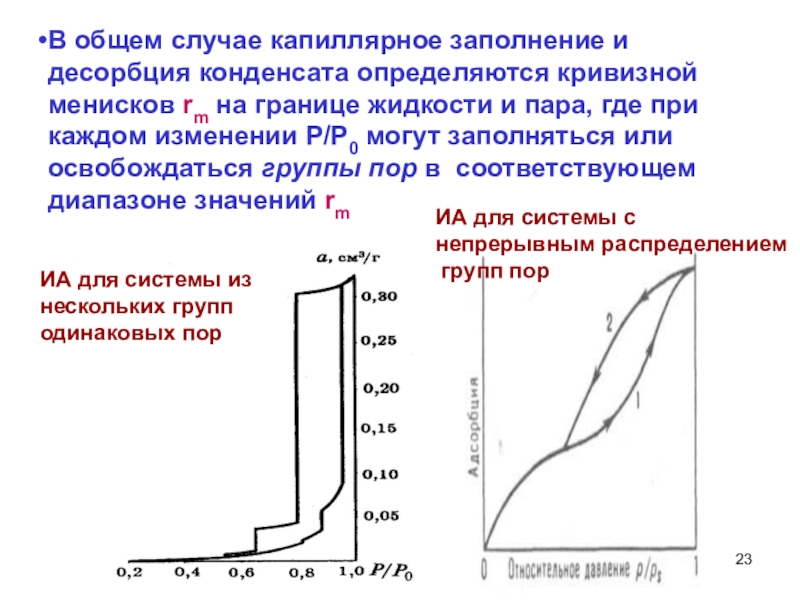
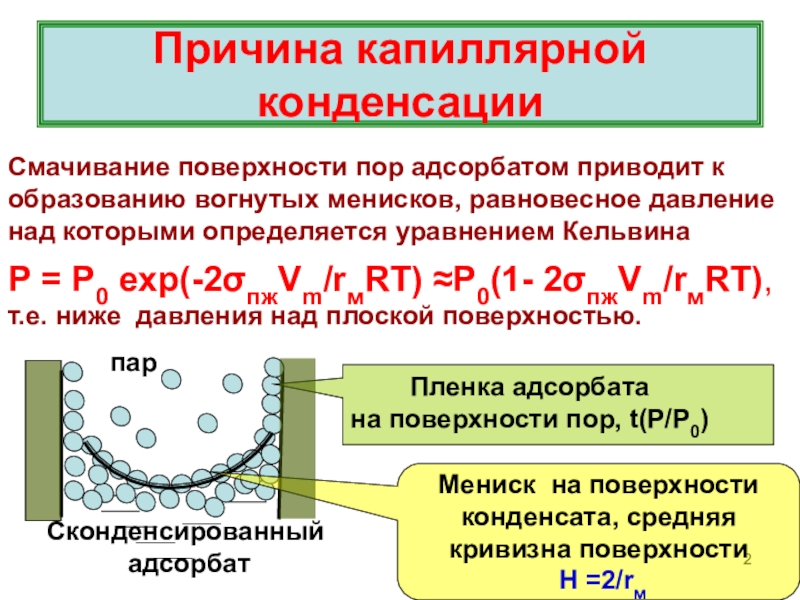
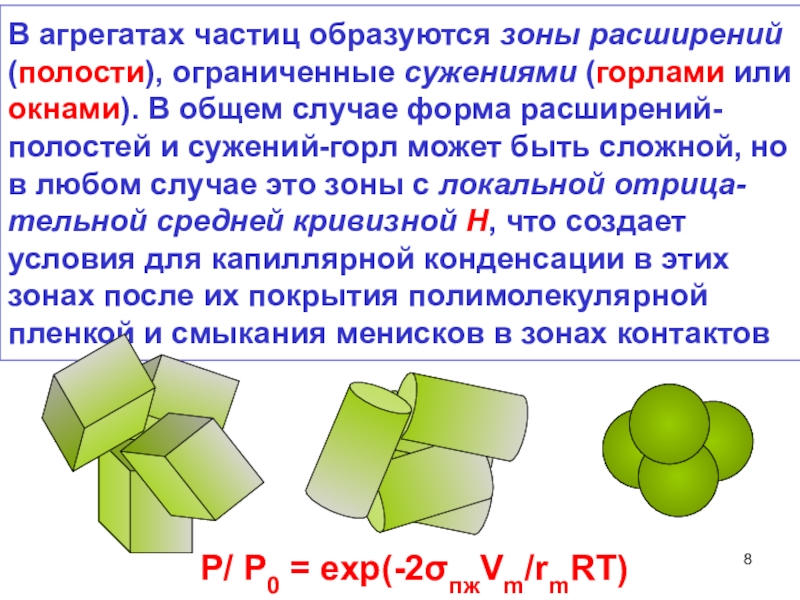
с объемным заполнением мезопор при относительном давлении паров Р/Р0< 1.

Необходимые условия КК: наличие мезопор, смачиваемость их поверхности жидкой фазой адсорбата, температура ниже критической Ткр для адсорбата (при Т > Ткр КК не возможна).
КК можно рассматривать как фазовый переход
1 рода: пар→ж (заполнение на адс. ветви) и ж → пар (испарение при десорбции).

давления над плоской поверхностью.
Смачивание поверхности пор адсорбатом приводит к
образованию

вогнутых менисков, равновесное давление
над которыми определяется уравнением Кельвина

и необратимой (с гистерезисом).
В случае обратимости внешняя форма ИА

аналогична получаемой для непористых или макропорис-тых систем и может быть выявле-на, например, сравнительным анализом с ИА на действительно непористых материалах

Область начала
КК

= ехр(+2пжVm/rmRT)
Растет только полимолекулярная пленка t(P/P0) на поверхности

средней кривизной Н, что создает условия для капиллярной конденсации в

этих зонах после их покрытия полимолекулярной пленкой

Р/ Р0 = ехр(-2пжVm/rmRT)

средней отрицательной кривизной.
Р/ Р0 = ехр(-2пжVm/rmRT)

или окнами). В общем случае форма расширений-полостей и сужений-горл может

быть сложной, но в любом случае это зоны с локальной отрица-тельной средней кривизной Н, что создает условия для капиллярной конденсации в этих зонах после их покрытия полимолекулярной пленкой и смыкания менисков в зонах контактов

Р/ Р0 = ехр(-2пжVm/rmRT)

поверхности
в зонах контактов (в простейшем случае –цилиндрические).
Их кривизна по

мере заполнения убывает (область обрати-
мой капиллярной конденсации). В момент смыкания тип
поверхности не меняется, но дальнейшее заполнение
повышает среднюю кривизну. Критическое значение
радиуса кривизны ~ радиус кривизны вписанного
цилиндра. Десорбция из такого элемента определяется
радиусом сферического мениска на торцах упаковки
Rп > Rг

упрощения – сферическое, то на дне образуется сферический мениск с

радиусом кривизны rm = R - t, который меньше радиуса кривизны цилиндрического мениска rm = 2(R - t).
Поэтому ситуация при к/к и десорбции из цилиндрической поры «с дном» существен-но отличается от ситуации в цилиндричес-кой поре без дна (изменение формы мениска)

Р/Р0=ехр[-пжVm/rmRT], Происходит спонтанное заполнение с образованием на торцах полусферических менисков

с дальнейшим дозаполнением до равновесных значений радиуса кривизны.
Десорбция в этом случае определяется менисками на торцах заполненного капилляра и происходит при давлении, соответствующем потере стабильности сферического мениска с rm=R - t (гистерезис при изменении формы мениска)

индивидуальной полости определяется радиусом кривизны полого цилиндра, а десорбция

– радиусом кривизны сферы
(Р/Р0) адс >(P/Po)дес
Гистерезис при изменении типа кривизны поверхности

Р/Р0

а



размера и формы
Ближайшее окружение полости простейшей формы может влиять

на особенности ее заполнения при адсорбции и освобождения при десорбции (кооперативные эффекты при адсорбции и десорбции) с соответствующим проявлением гистерезиса

разными размерами R1

соседнем капилляре:
переход от ситуации «заполнение полости без дна»
к «заполнению полости с дном»:

менисков rm на границе жидкости и пара, где при каждом

изменении Р/Р0 могут заполняться или освобождаться группы пор в соответствующем диапазоне значений rm

геометрическими особенностями данного элемента и его ближайшего окружения «ближний порядок),

а десорбция – его связью с внешней поверхностью гранулы или поверхностью незаполненных макропор или (дальний порядок).