Кинематика поступательного движения

t в уравнениях (2.1) и (2.2) получим уравнение траектории движения

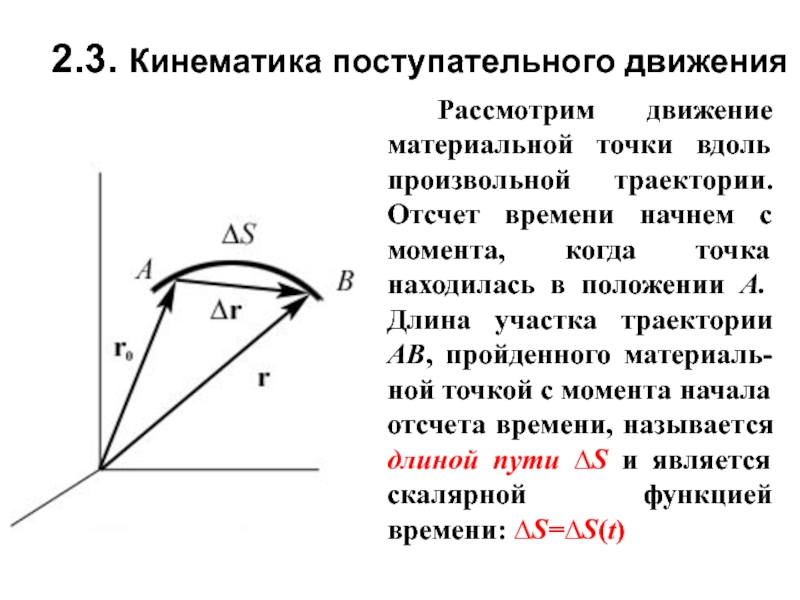
материальной точки.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве.
В зависимости от формы траектории движение может быть прямолинейным (поступательным), криволинейным и вращательным.

Отсчет времени начнем с момента, когда точка находилась в положении

А. Длина участка траектории АВ, пройденного материаль-ной точкой с момента начала отсчета времени, называется длиной пути ∆S и является скалярной функцией времени: ∆S=∆S(t)

криволинейной траектории так, что в момент времени t ей соответствует

радиус–вектор . В течение малого промежутка времени точка пройдет путь ∆S и получит элементарное (бесконечно малое ) перемещение

Вектором средней скорости < > называется приращение радиус–вектора точки к промежутку времени Δt :
(2.3)

2.4. Скорость

фиксированный момент времени.
Мгновенная скорость – векторная величина, равная первой производной

радиус–вектора движущейся точки по времени.

2.4. Скорость

касательной, то вектор скорости направлен по касательной к траектории в

сторону движения, поэтому модуль мгновенной скорости




Таким образом, модуль мгновенной скорости равен первой производной пути по времени
(2.4)

2.4. Скорость

течением времени изменяется. В данном случае пользуются скалярной величиной

– средней скоростью неравномерного движения . Из рис. 3 вытекает, что , так как , и только в случае прямолинейного движения .
Если выражение ds=υdt (см. формулу 2.4) проинтегрировать по времени в пределах от t до t+∆t, то найдем длину пути, пройденного точкой за время ∆t:


(2.5)

2.4. Скорость

мгновенной скорости постоянно; тогда выражение (2.5) примет вид:

Длина пути, пройденного точкой за промежуток времени от t1 до t2 дается интегралом:

2.4. Скорость

Содержание

как быстро изменяется скорость с течением времени.

Физической величиной характеризующей быстроту изменения скорости по модулю и направлению является ускорение.
Рассмотрим плоское движение, то есть движение, при котором все участки траектории точки лежат в одной плоскости.
Пусть вектор задает скорость точки А в момент времени t. За время Δt движущаяся точка перешла в положение В и приобрела скорость, отличную от как по модулю, так и по направлению и равную

2.5. Ускорение и его составляющие.

(рис.4).
Разложим вектор на две составляющие. Для

этого из точки А (рис.4) по направлению скорости
отложим вектор , по
модулю равный . Очевидно, что вектор , равный Δυτ, определяет изменение скорости за время Δt по модулю:
Δυτ=υ1-υ

Рис. 4

Вторая же составляющая характеризует изменение скорости за время Δt по направлению.

скорости, определяя тем самым быстроту изменения скорости по модулю.
Найдем вторую

составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому можно считать дугу окружности радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и ЕАД следует Δυn /AB= Δυ1 /r, но т.к. AB = υ·Δt , то

.
Поскольку

, угол ЕАD стремится к нулю, и т.к. треугольник ЕАD равнобедренный, то угол АDЕ между
и стремится к прямому. Следовательно, при ∆t→0 векторы и оказываются взаимно перпен-дикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор , перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения равная

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена

по касательной к траектории), а нормальная составляющая ускорения – быстроту изменения скорости по направлению (направлена к центру кривизны траектории).

классифицировать следующим образом:
1. aτ = 0, an= 0 – прямолинейное

равномерное движение;

2. aτ = a = const, an = 0 – прямолинейное
равнопеременное движение.

При таком виде движения .

Если начальный момент времени t1=0 , а начальная скорость υ1 =υ0, то, обозначив t2= t и υ2 =υ, получим a = (υ - υ0)/t, откуда

с

переменным ускорением.

4. aτ = 0, an=const.
При aτ = 0 скорость по модулю не меняется, а изменяется по направлению. Из формулы an= υ2/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным.

Проинтегрировав эту формулу в пределах от нуля до произвольного момента t, найдем, что длина пути пройденного точкой, в случае равнопеременного движения

движение.

6. aτ = const, an ≠ 0 – криволинейное равнопеременное
движение.

7. aτ = f(t), an ≠ 0 - криволинейное движение
с переменным ускорением.

Содержание

гладкой полусферы радиуса R.  На какой высоте он оторвётся от

поверхности. Ответ: 2R/3
Цилиндр радиуса R лежит на двух тонких стержнях. С какой относительной скоростью V должны раздвигаться стержни, чтобы падения цилиндра происходило без контакта с ними. Ответ:
С какой скоростью шарик должен двигаться по верхней ступени лестницы, чтобы удариться о среднюю и нижнюю ступень только по одному разу. Ширина и высота ступеней - b. Ответ:

гравитационного поля Земли на примере выстрела из пушки. Если пушка

расположена в точке с коорди-натами (0, 0, 0), то снаряд будет двигаться по траектории, которая описывается следующими уравнениями:

X=(υcosϕ)t Y = (υsinϕ)t - gt2/2,
где υ - скорость снаряда вдоль ствола пушки,  ϕ - угол между стволом пушки и горизонтом (ось X), t - время, g - ускорение свободного падения в поле тяжести Земли. Подставляя t из первого уравнения во второе, находим уравнение траектории движения снаряда:
Y = X tg ϕ - (g/2 υ 2)(1 + tg2 ϕ) X2

Дальше

параболическую форму. Из этого уравнения находим максимальную дальность стрельбы  Xmax

(при этом Y=0) и максимальную высоту полёта Ymax (первая производная Y по координате X равна нулю):
Xmax = υ2sin(2 ϕ)/g Ymax = υ2sin2 ϕ/2g
Из первого уравнения видно, что максимальная дальность полёта снаряда достигается при стрельбе под углом  ϕ, равном 45°.

Назад