КЛАСТЕРНЫЙ АНАЛИЗ

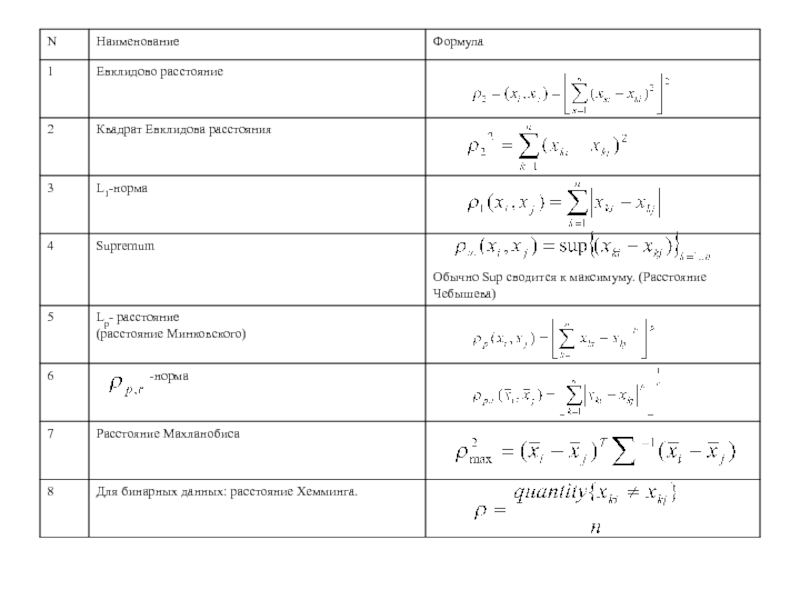
на основании данных , находящихся в множестве Х разбить их

на m групп таким образом , чтобы


Такое разбиение должно отвечать некоторому критерию сходства, т.е. элементы из одного класса отвечают критерию сходства, а элементы из разных классов- нет.
Имеется некоторая целевая функция, которая определяет правило, по которому мы относим элементы к тому или иному классу. Предполагается, что каждый элемент относится строго к одному классу- это детерминированная постановка задачи.
Кластеризация может быть и нечетной. Может быть вероятностная постановка задачи кластеризации.
Существует задача разделения смесей, когда по совместной выборке необходимо оценить характеристики классов.
Мы будем рассматривать кластерный анализ в детерминированном смысле.
Задача классификации может решаться очень успешно, если вначале провести кластеризацию.

чем базируется задача кластеризации:
Результат кластеризации зависит от критерия, по которому

будет проходить кластеризация. Большинство методов основано на понятии расстояния между объектами.

метрические методы основаны функции расстояния между объектами.

линейному преобразованию.





(Нужно доказать свойство инвариантности. Выписать формулы
и т.д.)
Если имеется

m объектов, то можно определить матрицу расстояний между этими объектами для каждой пары xi и xj
Условно обозначим

следующим образом:
и обладают следующими свойствами:









rij-коэффициент корреляции.

то rij определяется немного не так.

Меру сходства очень просто

построить из меры расстояния:





Фактически это обратная функция
Может быть мера сходства для бинарных объектов , которая определяется следующим образом:



-число совпадений единиц (если все совпадают, то Sij =1,если нет, то Sij =0)
nij -число совпадений нулей

это расстояние, которое определяется минимальным расстоянием между элементами рассматриваемых кластеров.

объектами)




Расстояние между центрами тяжести (или между математическими ожиданиями)
средний вектор.

Расстояние по

принципу средней связи.

–элементов в Xi:
Мы можем ввести функцию разброса:







Здесь можно минимизировать только

положение mi.
Этот критерий хорошо работает, когда предполагается, что кластеры хорошо разнесены.

образом:






Где Si -матрица рассеяния внутри группы, Sw – суммарная матрица

рассеяния внутри группы.
Есть понятия расстояния между группами:



где -общее среднее, ST – общее рассеивание

на минимизации определителя матрицы рассеивания (данный критерий эквивалентен линейным преобразованиям):

классифицированы по объему выборки .

1) Малые выборки (10-100 объектов)
2)

Большие выборки (100-1000 и больше объектов)

Задачи кластеризации с точки зрения априорной информации:

1) Число кластеров априорно задано
2)Число кластеров априорно не задано и их нужно определить
3)Число кластеров априорно не задано, но не требуется их точно определять в процессе обработки информации

Имеются следующие виды процедур:

1)Иерархические. Они отличаются большим объемом вычислений.
2)Параллельные процедуры. На каждом шагу анализируется вся выборка.
3)Процедуры последовательного типа: на каждом шагу анализируется один элемент выборки. Цель-минимизация некоторого функционала разбиения.

переборы
N-количество элементов



Пример: N=500 c=5, тогда полных переборов: М

и хj
передвигаем эту выборку в xj

(физически она остается на месте в пространстве, но относится уже к хj)
Критерий качества:

i->j , то


(2)




(старые х)

, а это будет тогда, когда

разделение по группам .
x1,x2,…xc Пусть с известно.
Вычисляем I и

средние m1,m2,…mc .
Цикл:
2) выбрать следующую выборку кандидата на передвижение
3) если Ni =1 , то перейти к следующему, иначе вычислить:




4) Передвинуть x в ХК ,если для всех I

5) Вновь вычислить I =

к Цикл
N- число выборок
Это типичная последовательная процедура.

d , можно задать любое расстояние, Евклидово, Махланобиуса и т.д.
Каждый

группа описывается средним:
Отличия к группе определяются как:

средних
2. Классифицируем n-выборок, разбивая их на классы по ближайшим соседям
3. Вновь

вычисляем среднее как среднее значение выборок в своем классе.
4. Если какое-либо среднее изменило значение, переходим в Цикл, иначе остановка
5. остановка.

минимизирует сумму квадратов расстояний всех точек, входящих в кластерную область,

до центра кластера структура алгоритма состоит из к-шагов.
Шаг 1. Выбираем К исходных центров кластеров


Этот выбор производится произвольно и обычно в качестве исходных центров кластеров используем первые к- результатов выборки из заданного множества образов.
Шаг 2. На к-том шаге итерации заданное множество образов {x} распределяется по к- кластерам по правилу мин расстояния:


для всех i=1,2… к: , Sj(k) - множество образов, входящих в кластер с центром zj(k)
В случае равенства решения принимается произвольным образом

центры кластеров
zj(k+1), j=1,2,…k. Исходя из условия, что сумма

квадратов расстояний между всеми образами принадлежит множеству Sj(k) и новым центрам кластера д.б. минимально,
таким образом, новый центр кластера выбирается так, чтобы минимизировать показатель качества


центр zj(k+1), обеспечивающий минимизацию показателя качества, является, в сущности, выборочным средним, определенным по множеству Sj(k). Как



Nj- число выборочных образов, входящих в множество Sj(k)

меняется от N (число выборок) до 1.
Основаны на построении деревьев,

описывающих взаимосвязи между кластерами.

x3, … xN
* * * … *
Используем

матрицу взаимных расстояний, т.к. каждый кластер состоит из 1-го элемента
Ищутся классы, ближайшие по данной ветке. Получаем следующее разбиение S(2), которой соответствует расстояние и так далее:




Но на каком-то этапе можем получить довольно устойчивую кластеризацию.

, N

- количество элементов выборок
цикл:
2) Если , то остановка
- заданное количество кластеров, текущее количество кластеров
3) Найти ближайшую пару кластеров xi , xj
4) Объединяем xi и xj и уничтожаем хi . Положить -1
5) Переход к циклу.
Аналогично можно осуществлять эту процедуру и снизу.