Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кодирование информации в компьютере
Содержание
- 1. Кодирование информации в компьютере
- 2. Представление чиселДля записи информации о количестве объектов
- 3. Позиционные и непозиционные системы счисленияВсе системы счисления
- 4. Позиционные системы счисленияПервая позиционная система счисления была
- 5. Основание системы счисленияКоличество различных символов, используемых для
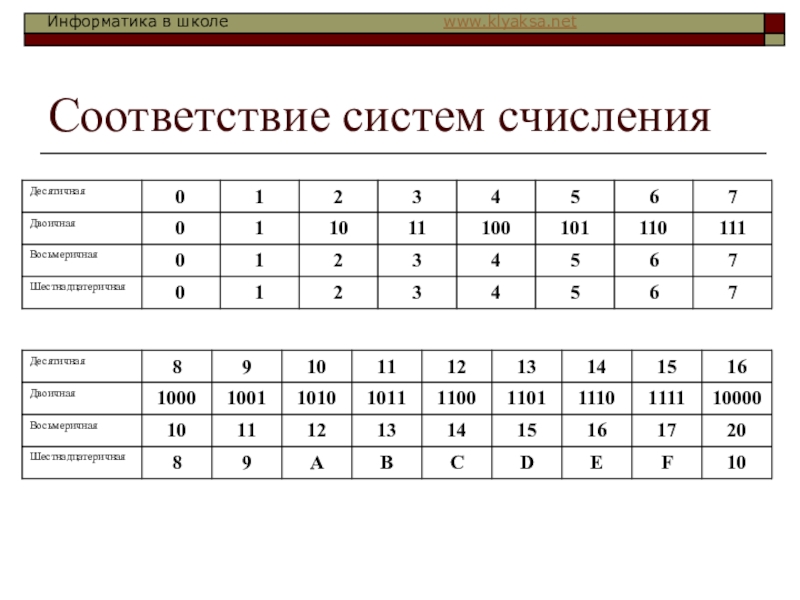
- 6. Соответствие систем счисления
- 7. Двоичное кодирование текстовой информацииДля кодирования одного символа
- 8. Перевод чисел из одной системы счисления в
- 9. Перевод чисел из одной системы счисления в
- 10. В позиционной системе счисления с основанием q
- 11. Aq =±(an–1 qn–1+ an–2 qn–2+…+
- 12. Двоичная система счисленияДвоичной системой счисления называется позиционная
- 13. Правило перевода целых десятичных чисел в двоичную
- 14. 1) последовательно выполнять деление данного числа и
- 15. Каждый знает, что дроби бывают обыкновенные и
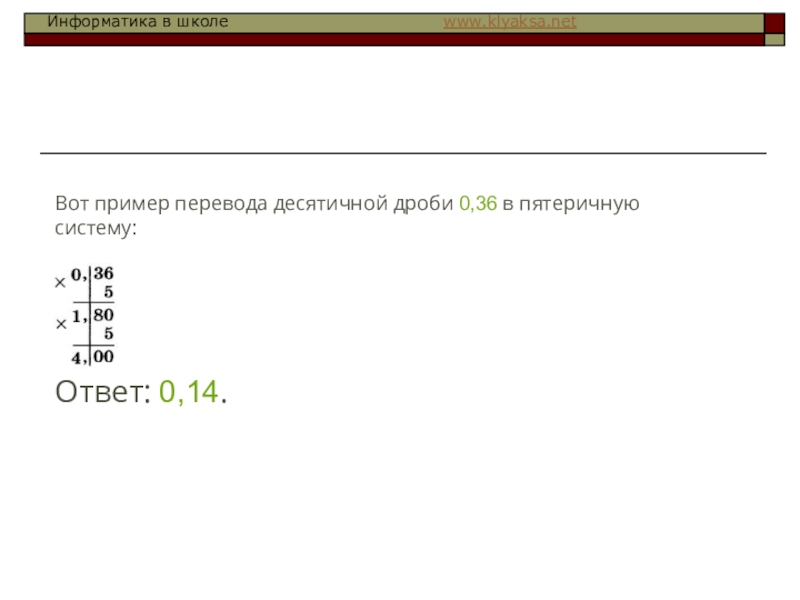
- 16. Вот пример перевода десятичной дроби 0,36 в пятеричную систему: Ответ: 0,14.
- 17. Обратите внимание: после четвертого умножения мы снова
- 18. Перевод целых десятичных чисел в любую другую
- 19. Пример перевода из двоичной в десятичную систему
- 20. Еще раз повторим алгоритм перевода чисел из
- 21. Для перевода смешанного числа в десятичную систему
- 22. Переведите десятичное число 0,816 в двоичную систему
- 23. Переведем целую часть числа в двоичную систему:Переведем
- 24. Спасибо за внимание
- 25. Слайд 25
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Представление чисел
Для записи информации о количестве объектов используются числа. Числа
записываются с использование особых знаковых систем, которые называют системами счисления.
счисления – совокупность приемов и правил записи чисел с помощью определенного набора символов.Слайд 3Позиционные и непозиционные системы счисления
Все системы счисления делятся на две
большие группы:
Количественное значение каждой цифры числа зависит от того, в
каком месте (позиции или разряде) записана та или иная цифра.0,7 7 70
Количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.
XIX
Слайд 4Позиционные системы счисления
Первая позиционная система счисления была придумана еще в
Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней
использовалось шестьдесят цифр!В XIX веке довольно широкое распространение получила двенадцатеричная система счисления.
В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
Слайд 5Основание системы счисления
Количество различных символов, используемых для изображения числа в
позиционных системах счисления, называется основанием системы счисления.
Слайд 7Двоичное кодирование текстовой информации
Для кодирования одного символа требуется один байт
информации.
Учитывая, что каждый бит принимает значение 1 или 0, получаем,
что с помощью 1 байта можно закодировать 256 различных символов.28=256
Слайд 8Перевод чисел из одной системы счисления в другую
Чтобы перевести число
из позиционной системы счисления с основанием p в десятичную, надо
представить это число в виде суммы степеней p и произвести указанные вычисления в десятичной системе счисления.Например, переведем число 10112 в десятичную систему счисления. Для этого представим это число в виде степеней двойки и произведем вычисления в десятичной системе счисления.
10112 = 1*23 + 0*22 + 1*21 + 1*20 = 1*8 + 0*4 + 1*2 + 1*1 = 8 + 0 + 2 + 1 = 1110
Рассмотрим еще один пример. Переведем число 52,748 в десятичную систему счисления.
52,748 = 5*81 + 2*80 + 7*8-1 + 4*8-2 = 5*8 + 2*1 + 7*1/8 +4*1/64 = 40 + 2 + 0,875 + 0,0625 = 42,937510
Слайд 9Перевод чисел из одной системы счисления в другую
Перевод из десятичной
системы счисления в систему счисления с основанием p осуществляется последовательным
делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.Переведем десятичное число 2010 в двоичную систем счисления (основание системы счисления p=2). В итоге получили 2010 = 101002.
Слайд 10В позиционной системе счисления с основанием q любое число может
быть представлено в виде:
Aq =±(an–1qn–1+ an–2 qn–2+…+ a0
q0+ a–1q–1+…+ a–m q–m) Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
Основная формула
Слайд 11Aq =±(an–1 qn–1+ an–2 qn–2+…+ a0 q0+
a–1 q–1+…+ a–m q–m)
Примеры записи чисел в
развёрнутой форме:2012=2103 +0102 +1101 +2100
0,125=110-1 +210-2 +510–3
14351,1=1104 +4103 +3102 +5101 +1100 +110–1
Развёрнутая форма
Слайд 12Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с
основанием 2.
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно
записать:an–1an–2…a1a0 = an–12n–1 + an–22n–2 +…+ a020
Например:
100112 =124+023+022+121+120 = 24 +21 + 20 =1910
Правило перевода двоичных чисел в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа
Слайд 13Правило перевода целых десятичных чисел в двоичную систему счисления
an–12n–1+an–22n–2+… a121 +a0
= an–12n–2 +…+ a1 (остаток a0)
2
an–12n–1+an–22n–2+… a1= an–12n–3+…+ a2 (остаток a1)
2
. . .
an–12n–1+an–22n–2+… a2
= an–12n–4 +…+ a3 (остаток a2)
2
На n-м шаге получим набор цифр: a0a1a2…an–1
Слайд 141) последовательно выполнять деление данного числа и получаемых целых частных
на основание новой системы счисления до тех пор, пока не
получим частное, равное нулю;2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
Цифровые весы
Правило перевода целых десятичных чисел в систему счисления с основанием q
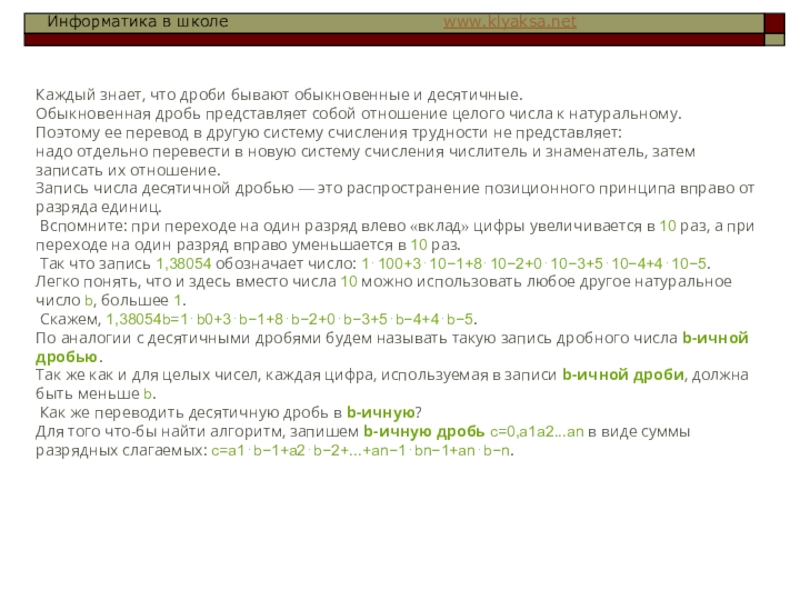
Слайд 15Каждый знает, что дроби бывают обыкновенные и десятичные.
Обыкновенная дробь
представляет собой отношение целого числа к натуральному.
Поэтому ее перевод
в другую систему счисления трудности не представляет: надо отдельно перевести в новую систему счисления числитель и знаменатель, затем записать их отношение.
Запись числа десятичной дробью — это распространение позиционного принципа вправо от разряда единиц.
Вспомните: при переходе на один разряд влево «вклад» цифры увеличивается в 10 раз, а при переходе на один разряд вправо уменьшается в 10 раз.
Так что запись 1,38054 обозначает число: 1⋅100+3⋅10−1+8⋅10−2+0⋅10−3+5⋅10−4+4⋅10−5.
Легко понять, что и здесь вместо числа 10 можно использовать любое другое натуральное число b, большее 1.
Скажем, 1,38054b=1⋅b0+3⋅b−1+8⋅b−2+0⋅b−3+5⋅b−4+4⋅b−5.
По аналогии с десятичными дробями будем называть такую запись дробного числа b-ичной дробью.
Так же как и для целых чисел, каждая цифра, используемая в записи b-ичной дроби, должна быть меньше b.
Как же переводить десятичную дробь в b-ичную?
Для того что-бы найти алгоритм, запишем b-ичную дробь c=0,a1a2...an в виде суммы разрядных слагаемых: c=a1⋅b−1+a2⋅b−2+...+an−1⋅bn−1+an⋅b−n.
Слайд 17
Обратите внимание: после четвертого умножения мы снова получили дробь 0,36.
Это
значит, что дальше процесс будет повторяться и никогда не закончится!
Тем самым после перевода числа 0,36 в семеричную систему счисления получается бесконечная периодическая дробь:
0,23432343...7= 0,(2343)7. При переводе конечной b-ичной дроби в десятичную систему тоже может получиться бесконечная дробь.
К примеру, запись 0,13 представляет одну треть и, следовательно, в десятичной системе будет выглядеть как бесконечная десятичная дробь 0,33333...=0,(3).
А теперь попытаемся перевести ту же дробь в семеричную систему счисления:
Слайд 18Перевод целых десятичных чисел в любую другую системы счисления осуществляется
делением числа на основание новой системы счисления до тех пор,
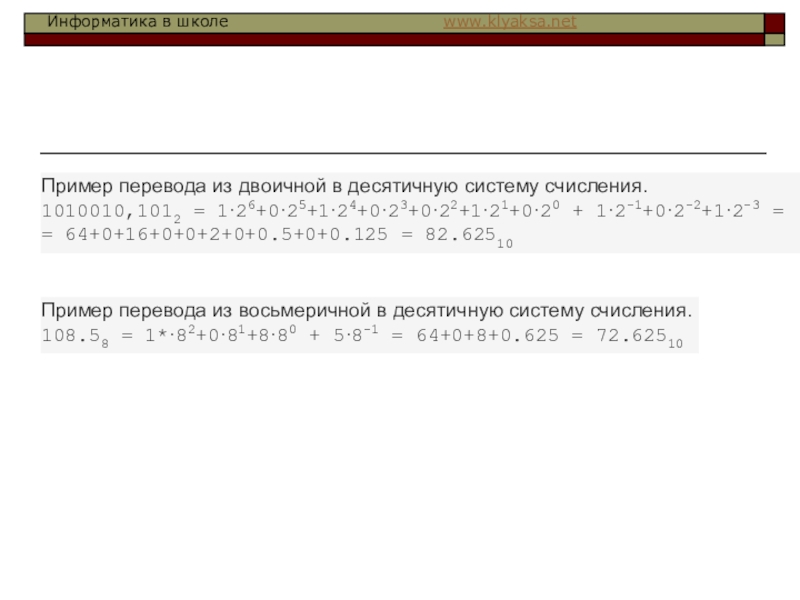
пока в остатке не останется число меньшее основания новой системы счисления. Новое число записывается в виде остатков деления, начиная с последнего. Перевод правильной десятичной дроби в другую ПСС осуществляется умножением только дробной части числа на основание новой системы счисления до тех пор пока в дробной части не останутся все нули или пока не будет достигнута заданная точность перевода. В результате выполнения каждой операции умножения формируется одна цифра нового числа начиная со старшего. Перевод неправильной дроби осуществляется по 1 и 2 правилу. Целую и дробную часть записывают вместе, отделяя запятой.Слайд 19Пример перевода из двоичной в десятичную систему счисления.
1010010,1012 = 1·26+0·25+1·24+0·23+0·22+1·21+0·20
+ 1·2-1+0·2-2+1·2-3 =
= 64+0+16+0+0+2+0+0.5+0+0.125 = 82.62510
Пример перевода из
восьмеричной в десятичную систему счисления.108.58 = 1*·82+0·81+8·80 + 5·8-1 = 64+0+8+0.625 = 72.62510
Слайд 20Еще раз повторим алгоритм перевода чисел из одной системы счисления
в другую ПСС
Из десятичной системы счисления:
разделить число на основание переводимой
системы счисления;найти остаток от деления целой части числа;
записать все остатки от деления в обратном порядке;
Из двоичной системы счисления
Для перевода в десятичную систему счисления необходимо найти сумму произведений основания 2 на соответствующую степень разряда;
Для перевода числа в восьмеричную необходимо разбить число на триады. Например, 1000110 = 1 000 110 = 1068
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить число на группы по 4 разряда. Например, 1000110 = 100 0110 = 4616
Слайд 21Для перевода смешанного числа в десятичную систему из любой другой
следует пронумеровать разряды числа, начиная с нуля, справа налево от
младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.Переведите число 105,4 из восьмеричной системы в десятичную.
Решение:
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :
Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
Слайд 22Переведите десятичное число 0,816 в двоичную систему с точностью до
сотых.
Решение:
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на
2 и выписываем целые части,начиная с первой: