КОЛЕБАНИЯ И ВОЛНЫ В ЗАМАГНИЧЕННОЙ ПЛАЗМЕ

Типичным случаем для низкотемпературной и высокотемпературной плазмы является

ее расположение во внешнем магнитном поле. Для лабораторной плазмы – это специально созданные сильные магнитные поля необходимые для магнитной термоизоляции плазмы, для космической плазмы – это магнитные поля Земли, Солнца, звезд и т.д. В некоторых случаях собственное магнитное поле плазмы в силу протекания сильных токов является достаточно значительным. Ввиду данных причин колебания и волны в плазме могут происходить в присутствии магнитных полей и имеют свою специфику. Первые наблюдения распространения плазменных волн в магнитосфере Земли были сделаны в начале XX века. Некоторые плазменные волны были предсказаны теоретически, как, например, альфвеновские, а затем были обнаружены в космической плазме и в плазменных установках.

магнитного поля в плазму. Будем считать, что плазма обладает очень

большой или в пределе бесконечной проводимостью. Этот случай возможен для высокотемпературной полностью ионизованной плазмы и упрощает теоретическое рассмотрение. Рассмотрим контур S, который движется вместе с плазмой и спустя время Δt занимает положение S’ (рис.1).
B


Рис.1

Предполагается, что если произойдет смещение данного контура поперек магнитного поля, то индуцируемые в плазме токи создадут такие магнитные поля, которые складываясь с исходным полем обеспечат постоянство магнитного потока:

или

Данный

принцип может существовать за счет высокой проводимости плазмы и связывается с вмороженностью силовых линий магнитного поля в плазму.
Рассмотрим волны в плазме, связанные с упругостью силовых линий магнитного поля в плазме. Предположим, что в плазме создано постоянное магнитное поле (рис.2) и рассмотрим тонкие магнитные трубки. Допустим, что произошло возмущение данных трубок в перпендикулярном направлении с помощью электрического поля.
B

Рис.2

В силу вмороженности плазмы, при изгибе магнитной трубки плазма увлечет за собой силовые линии магнитного поля.

конце, поперечная волна смещения может начать движение вдоль данной силовой

линии с определенной скоростью. Приведем вывод для величины показателя преломления и скорости данных волн.
Дрейфовая скорость в скрещенных электрическом и магнитном полях записывается в виде:


Элементарное смещение частиц плазмы в данных полях связано с ларморовским радиусом:


Поляризацию единицы объема (дипольный момент) можно представить следующим образом:

электрического поля в виде:


Выразим из последнего выражения

ε и подставим в него полученные формулы:




Полученную формулу для диэлектрической проницаемости плазмы можно теперь использовать для вывода скорости волн:

с выражением, стоящим под корнем, тогда формула для скорости альфвеновских

(магнитогидродинамических) волн представляется в виде:


Выражение для скорости данных волн впервые было получено шведским физиком Альфвеном (1942 г.). Скорость волн прямо пропорциональна магнитному полю, что было проверено в ряде экспериментов.
Для рассмотрения диэлектрической проницаемости плазмы напомним основные результаты для плазмы в отсутствии магнитного поля. Общим выражением для диэлектрической проницаемости водородной плазмы с учетом обоих компонент (электронной и протонной) является следующее:

Рис.3

Графическая зависимость для ε с учетом только электронной частоты выглядит следующим образом (рис.3). Волны распространяются в плазме при частотах ω>ωp, а показатель преломления принимает значения от 0 до 1.
Рассмотрим волны в плазме в присутствии магнитного поля. Положим, что магнитное поле направлено вдоль оси z и вдоль данной оси распространяется электромагнитная волна ( ) с частотой равной ω. Основные уравнения, которые используют для вывода диэлектрической проницаемости следующие: уравнение непрерывности, уравнение движения и уравнения Максвелла:

и запишем уравнение для возмущенной величины:

Запишем также

уравнения для возмущенных величин :



Приведем основные результаты, которые следуют из решения системы данных уравнений. Диэлектрическая проницаемость плазмы представляется в виде тензора:

εzz), которая может описывать плазму в отсутствие магнитного поля. Другие

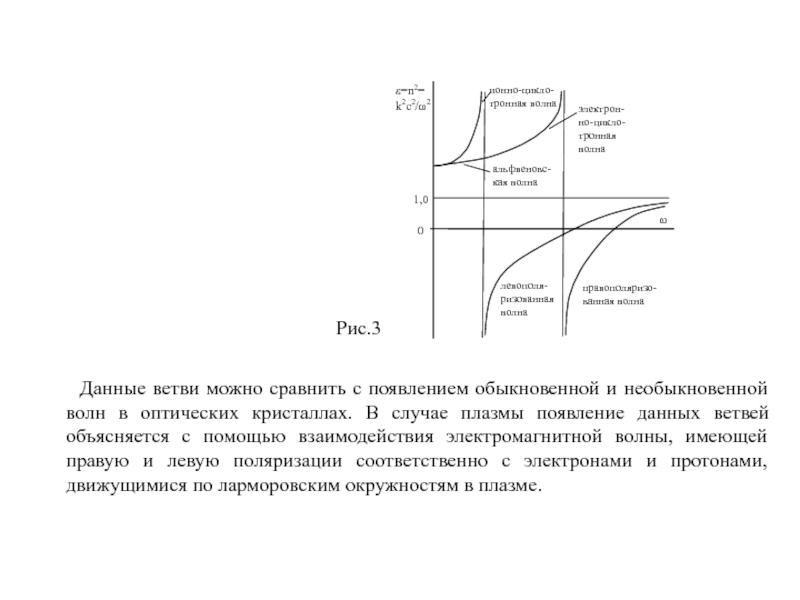
компоненты (ε1 и ε2) свойственны для плазмы в присутствии магнитного поля. Представим графическое изображение диэлектрической проницаемости в зависимости от частоты (рис.4). Сверху на графике расположены две низкочастотные ветви: ионно-циклотронная и электронно-циклотронная волны, а также альфвеновская волна. Следует заметить, циклотронные частоты и являются асимптотами для данных ветвей. Внизу на графике располагаются высокочастотные компоненты: левополяризованная волна и правополяризованная волны, которые отвечают за резонансное взаимодействие с протонной и электронной составляющими плазмы.

Рис.3

Данные ветви можно сравнить с появлением обыкновенной и необыкновенной волн в оптических кристаллах. В случае плазмы появление данных ветвей объясняется с помощью взаимодействия электромагнитной волны, имеющей правую и левую поляризации соответственно с электронами и протонами, движущимися по ларморовским окружностям в плазме.