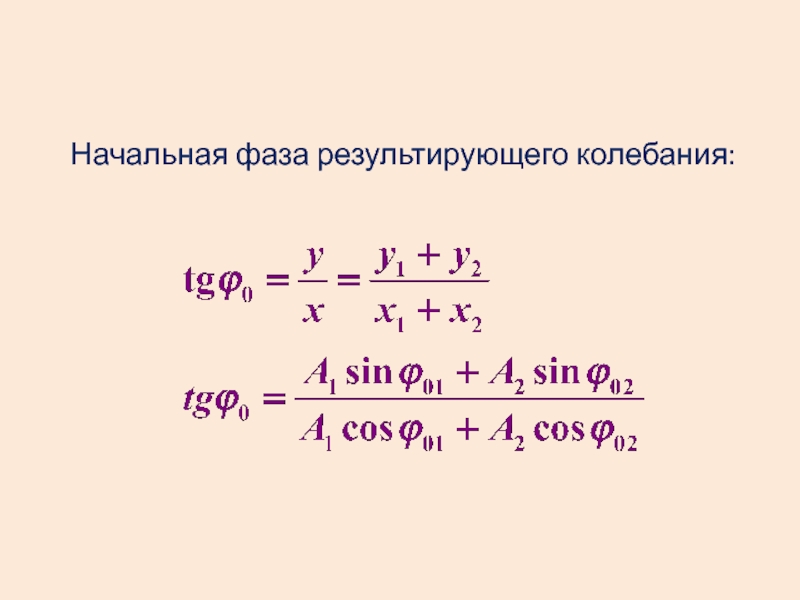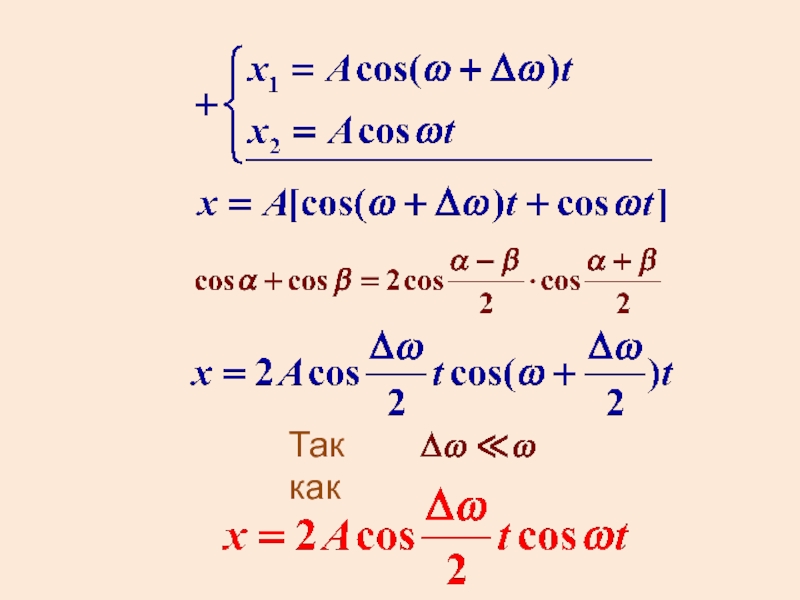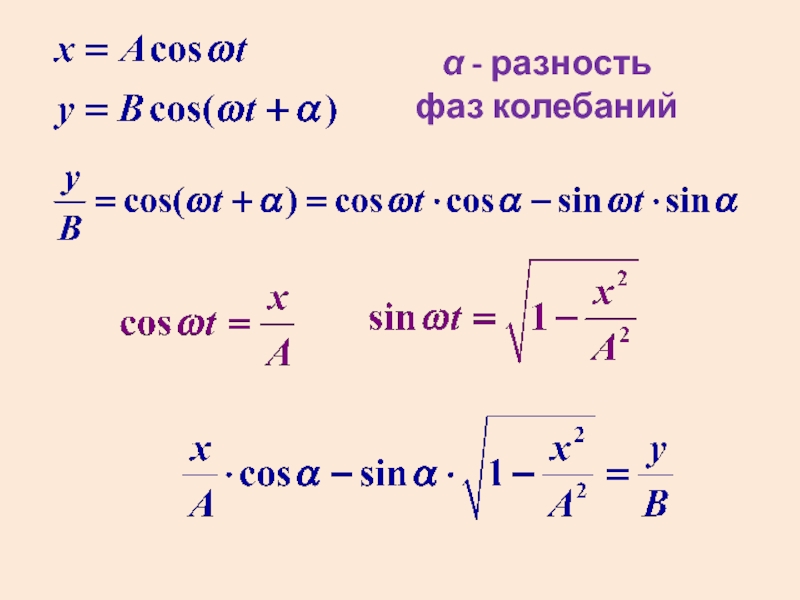Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КОЛЕБАНИЯ Колебания – это процессы, повторяющиеся во времени. По природе могут
Содержание
- 1. КОЛЕБАНИЯ Колебания – это процессы, повторяющиеся во времени. По природе могут
- 2. Физическую систему, совершающую колебания, называют осциллятором (маятником).
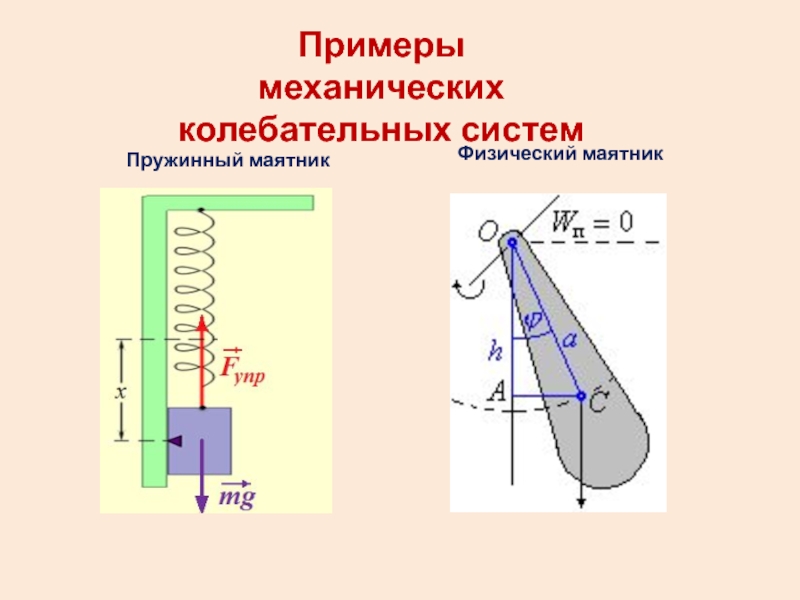
- 3. Примеры механических колебательных системПружинный маятникФизический маятник
- 4. Крутильный маятникМатематический маятник
- 5. Свободные (собственные) колебания происходят без переменных внешних
- 6. N – число колебаний, совершенных за время
- 7. Запишем второй закон Ньютона
- 8. Дифференциальное уравнение свободных гармонических колебаний
- 9. Гармонические колебания происходят по закону синуса или
- 10. A — амплитуда колебаний (максимальное значение колеблющейся
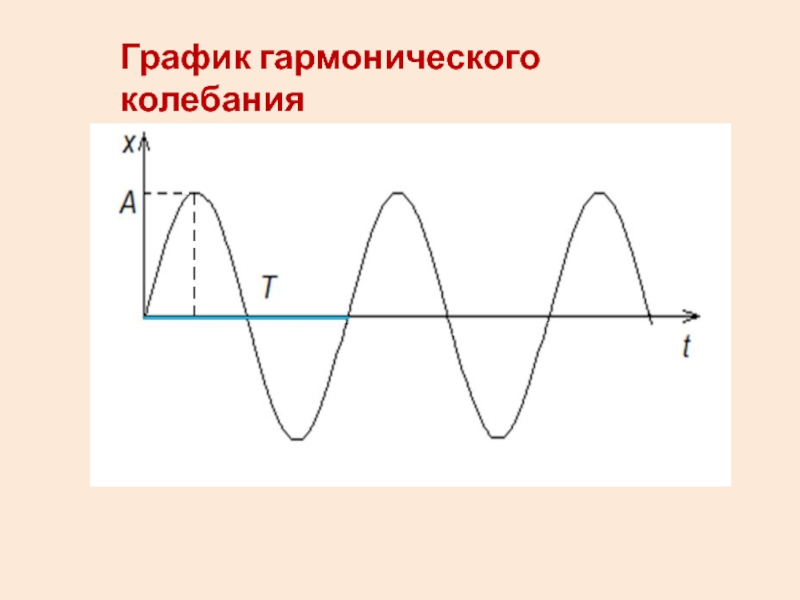
- 11. График гармонического колебания
- 12. Скорость и ускорение при гармонических колебанияхПусть МТ
- 13. Ускорение опережает координату по фазе на π радиан. Амплитуда ускорения:
- 14. Слайд 14
- 15. Энергия гармонического колебанияКинетическая:Потенциальная: и изменяются со сдвигом фаз π/2.Полная энергия:
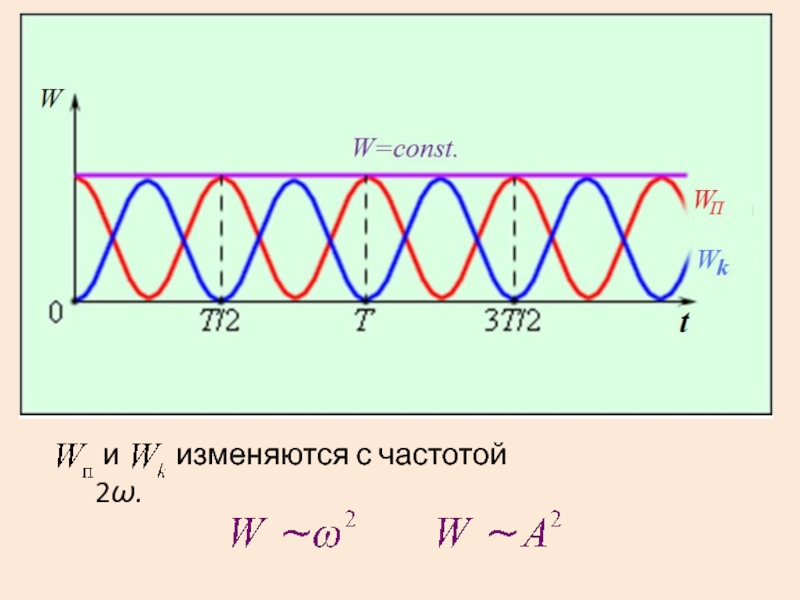
- 16. и изменяются с частотой 2ω.
- 17. Векторная диаграммаГармонические колебания можно представить в виде
- 18. x
- 19. Сложение колебаний одного направления Сложение колебаний
- 20. Пусть частоты колебаний равны.
- 21. Результирующую амплитуду находим по теореме косинусов.Если
- 22. Начальная фаза результирующего колебания:
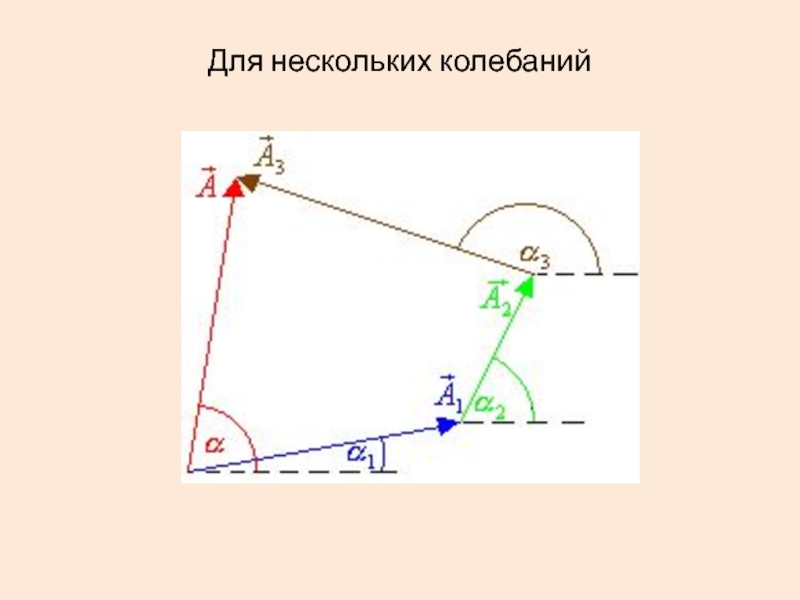
- 23. Для нескольких колебаний
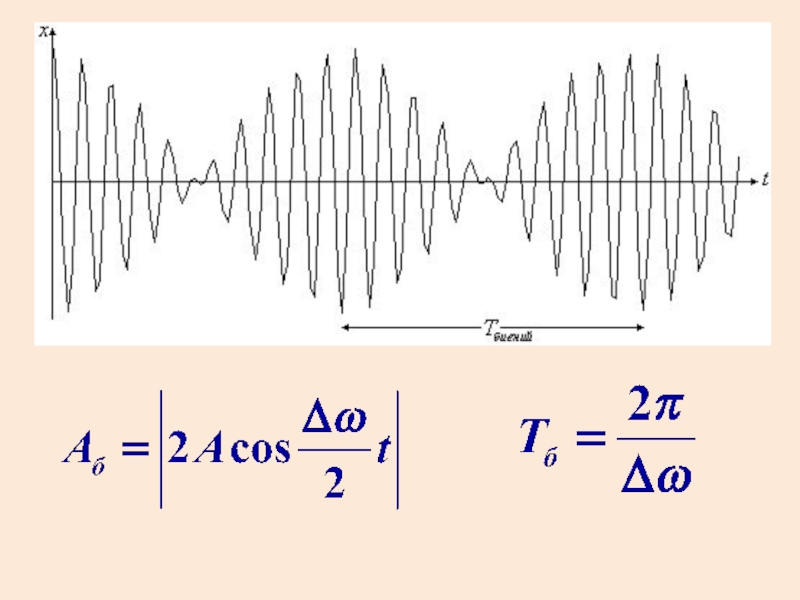
- 24. Биения При сложении однонаправленных колеба-ний неравных частот
- 25. Так как
- 26. Слайд 26
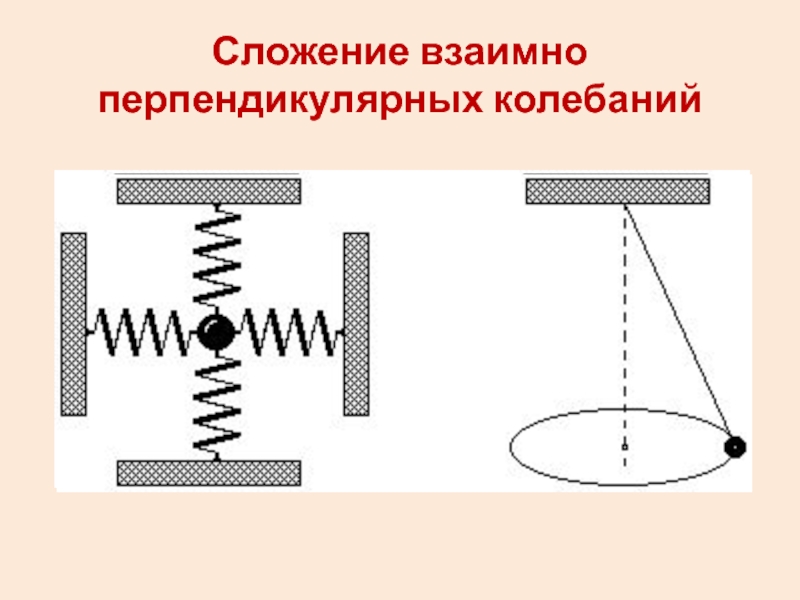
- 27. Сложение взаимно перпендикулярных колебаний
- 28. - разность фаз колебаний
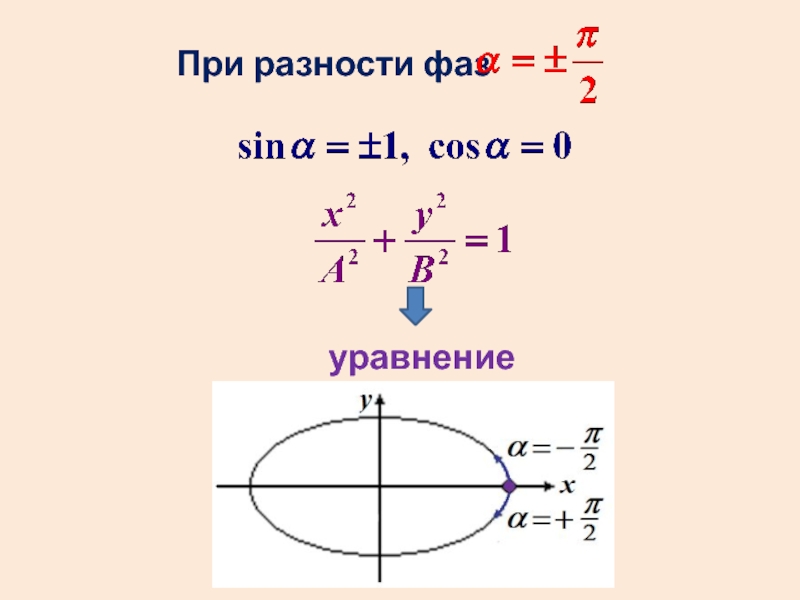
- 29. Уравнение эллипса
- 30. уравнение прямой линииПустьПусть уравнение прямой линии
- 31. При разности фаз уравнение эллипса
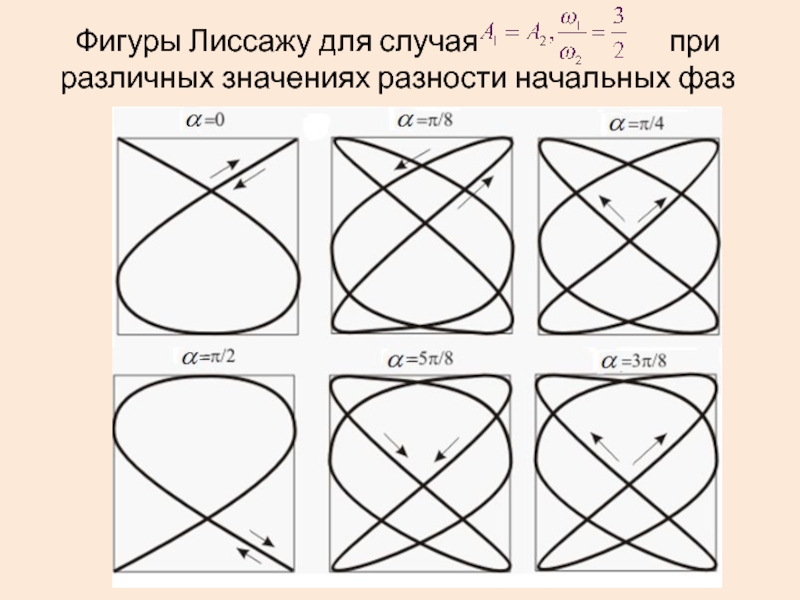
- 32. Фигуры Лиссажу для случая
- 33. Физический и математический маятникиФизический маятник - это
- 34. – расстояние от точки подвеса до центра массlПолучили диф. уравнение гармонического колебания .
- 35. Математический маятник – частный случай физического. Тело, подвешенное на нити, можно считать материальной точкой.Для математического маятникаm
- 36. Возьмем физический и математический маятники. Меняя длину
- 37. Точка O’ - это центр качания физического
- 38. Затухающие колебания Уравнение затухающих колебанийПусть на маятник
- 39. b — коэффициент затухания,
- 40. A0 - начальная амплитуда,- начальная фаза
- 41. Слайд 41
- 42. Характеристики затухания Время релаксации t — время,
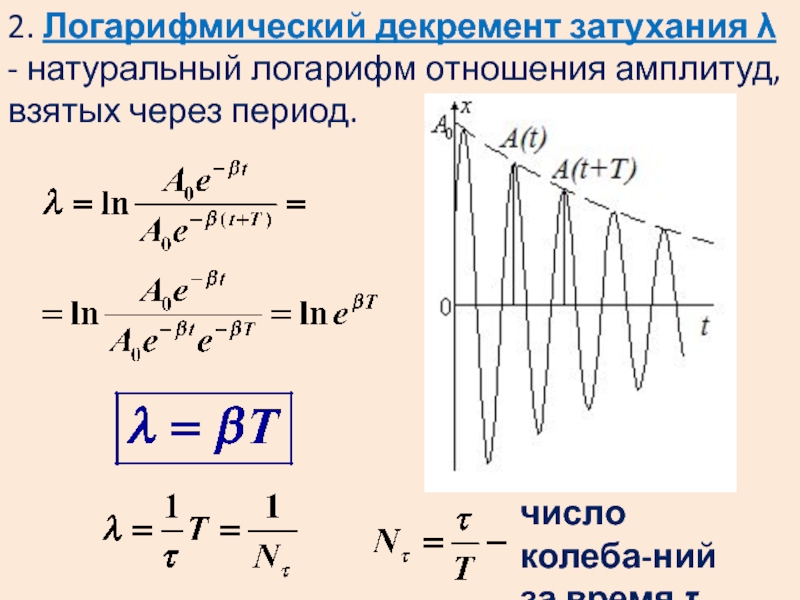
- 43. 2. Логарифмический декремент затухания - натуральный
- 44. Для мех. к.
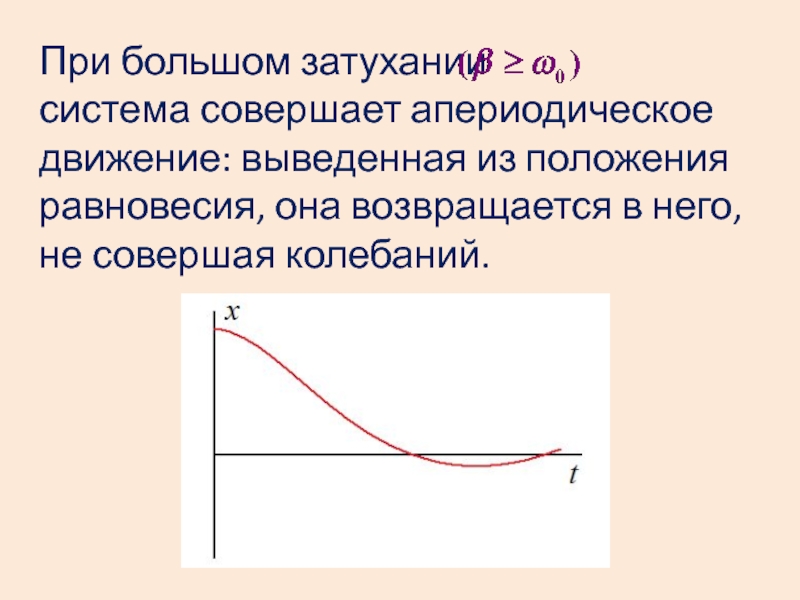
- 45. При большом затухании
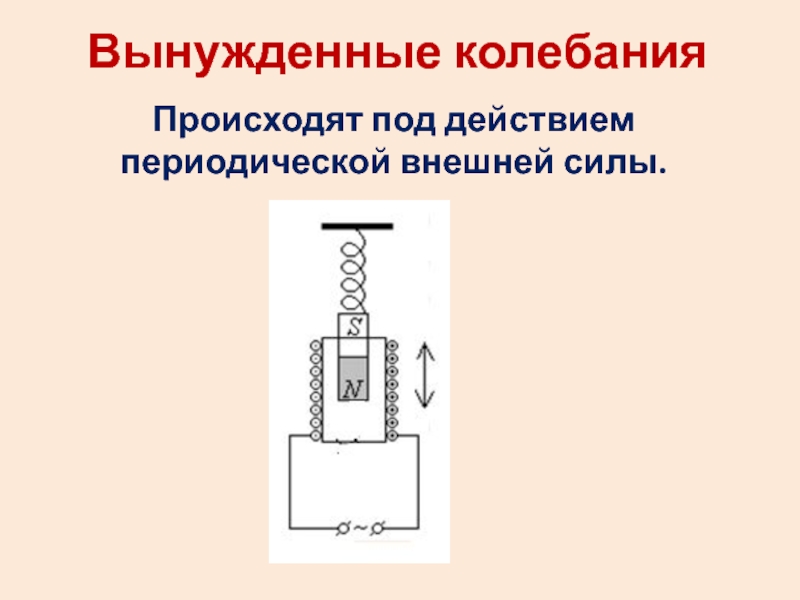
- 46. Вынужденные колебанияПроисходят под действием периодической внешней силы.
- 47. Добавим в уравнение движения периоди-ческую силу
- 48. Дифференциальное уравнение вынужденного колебанияРешение
- 49. Установившиеся вынужденные колебания - это гармонические колебания
- 50. Как А зависит от ?Пусть нет затухания
- 51. Если есть затухание (всегда), то ампли-туда колебаний
- 52. Резонансные кривые при разном уровне затухания
- 53. Если = 0 (статический случай), то
- 54. При малых по резонансной кривой можно определить добротность:
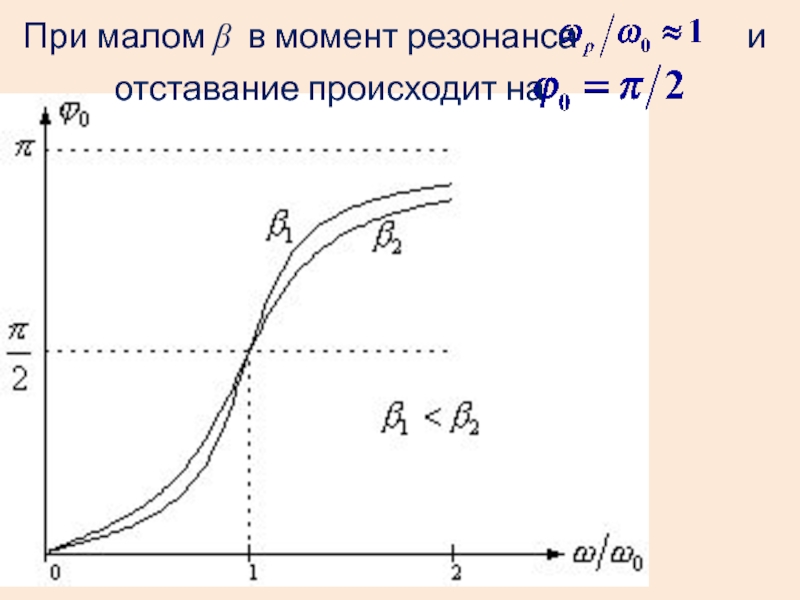
- 55. Вынужденные колебания отстают по фазе от колебаний вынуждающей силы на величину
- 56. . При малом b в момент резонанса
- 57. Слайд 57
- 58. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1КОЛЕБАНИЯ
Колебания – это процессы, повторяющиеся во времени.
По природе могут быть:
механическими;
электромагнитными;
тепловыми
и др.
Слайд 5Свободные (собственные) колебания происходят без переменных внешних воздействий.
Колебания периодические, если
значения изменяющихся величин повторяются через равные промежутки времени. Время одного
полного колебания - это период Т.Слайд 6N – число колебаний, совершенных за время t.
Частота колебаний –
это число колебаний в единицу времени.
Значит
Круговая (циклическая) частота – число
колебаний за 2π секунд. (Гц)
(рад./c)
Слайд 7Запишем второй закон Ньютона
:
Г.к. происходят под действием упругой или
квазиупругой силыГармонические колебания
Слайд 9Гармонические колебания происходят по закону синуса или косинуса.
х – значение
колеблющейся величины в момент времени t (отклонение от положения равновесия)
Решение
этого ур-яСлайд 10A — амплитуда колебаний (максимальное значение колеблющейся величины);
- циклическая частота;
-
начальная фаза колебаний.
Величина
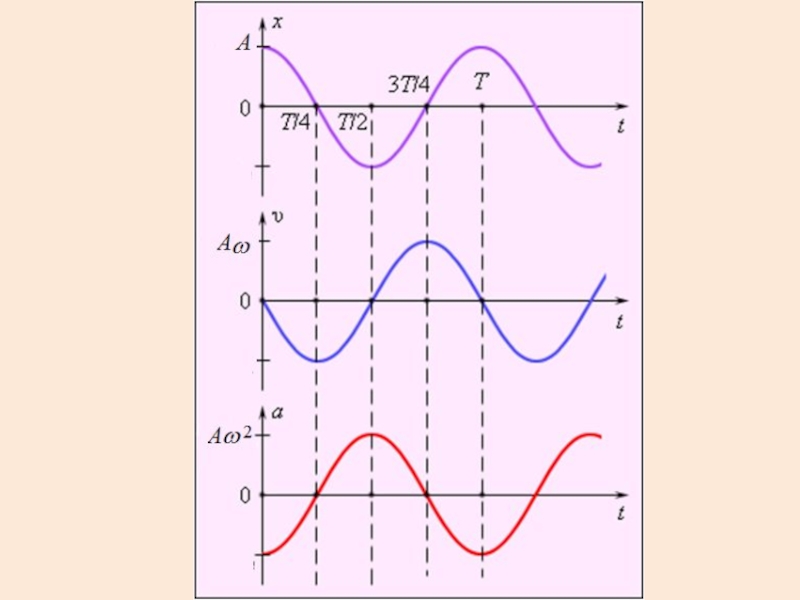
- это фаза колебаний. Именно она определяет значение х в данный момент времени.Слайд 12Скорость и ускорение при гармонических колебаниях
Пусть МТ совершает колебания вдоль
оси х.
Скорость опережает координату на π/2.
Амплитуда скорости:
Слайд 15Энергия гармонического колебания
Кинетическая:
Потенциальная:
и изменяются со сдвигом
фаз π/2.
Полная энергия:
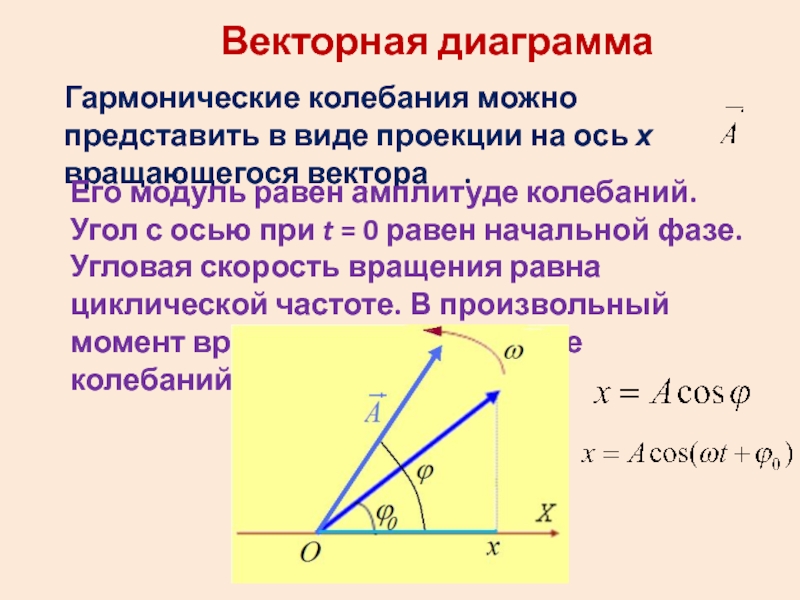
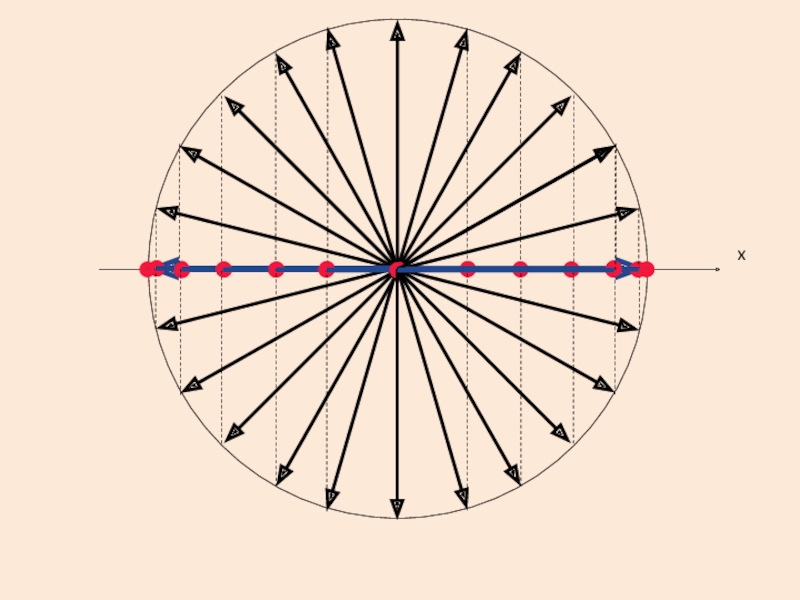
Слайд 17Векторная диаграмма
Гармонические колебания можно представить в виде проекции на ось
х вращающегося вектора .
Его модуль равен амплитуде колебаний.
Угол с осью при t = 0 равен начальной фазе. Угловая скорость вращения равна циклической частоте. В произвольный момент времени угол равен фазе колебаний.Слайд 21Результирующую амплитуду находим по теореме косинусов.
Если
,
то колебания происходят в одной фазе (синфазны). Тогда и
Если ,
то колебания происходят в противофазе. Тогда
Слайд 24Биения
При сложении однонаправленных колеба-ний неравных частот один вектор “обгоняет”
другой. Амплитуда результирующего коле-бания зависит от времени. Если частоты колебаний
близки, наблюдаются биения. Это периодические изменения амплитуды результирующего колебания.Пусть - разность частот колебаний. Начальную фазу примем равной нулю.
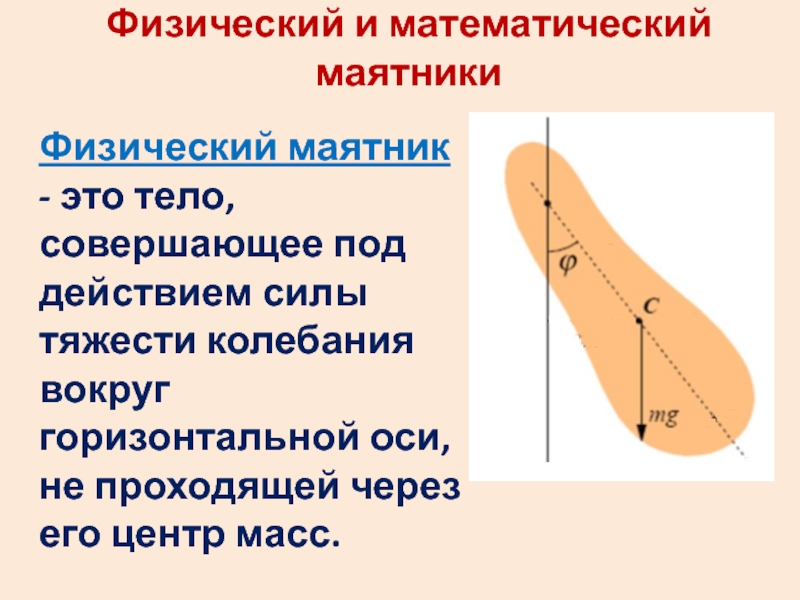
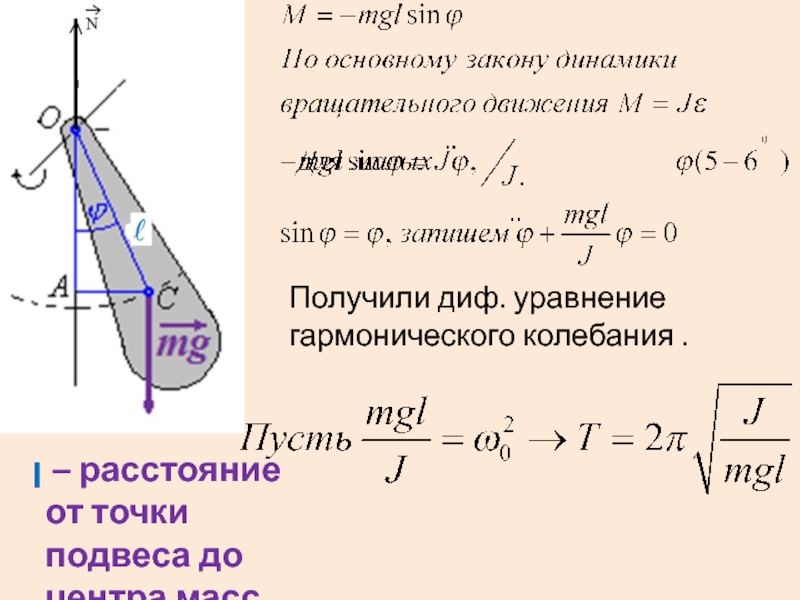
Слайд 33Физический и математический маятники
Физический маятник - это тело, совершающее под
действием силы тяжести колебания вокруг горизонтальной оси, не проходящей через
его центр масс.Слайд 34 – расстояние от точки подвеса до центра масс
l
Получили диф.
уравнение гармонического колебания .
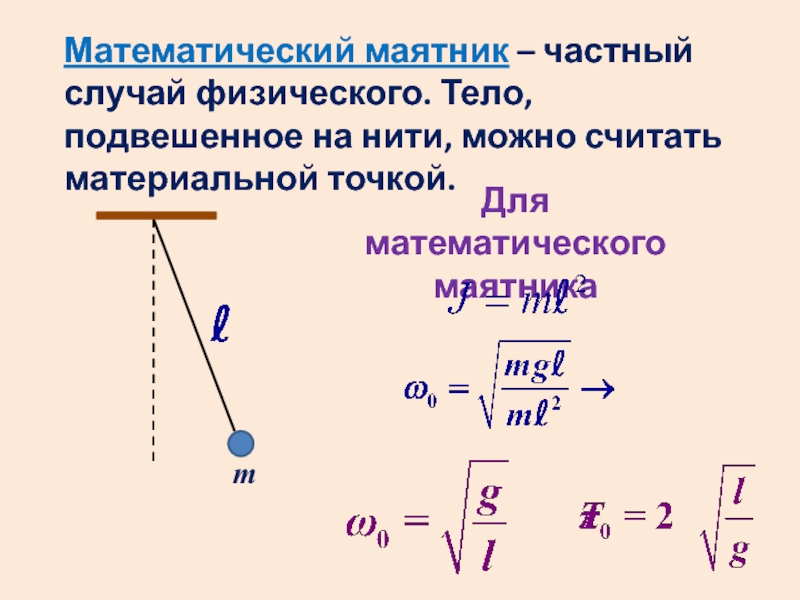
Слайд 35Математический маятник – частный случай физического. Тело, подвешенное на нити,
можно считать материальной точкой.
Для математического маятника
m
Слайд 36Возьмем физический и математический маятники. Меняя длину нити математичес-кого маятника
l, добьемся, чтобы периоды колебаний совпадали.Такую длину l назы-вают приведенной
длиной физического маятника. Обозначим ее L.мат.
физ.
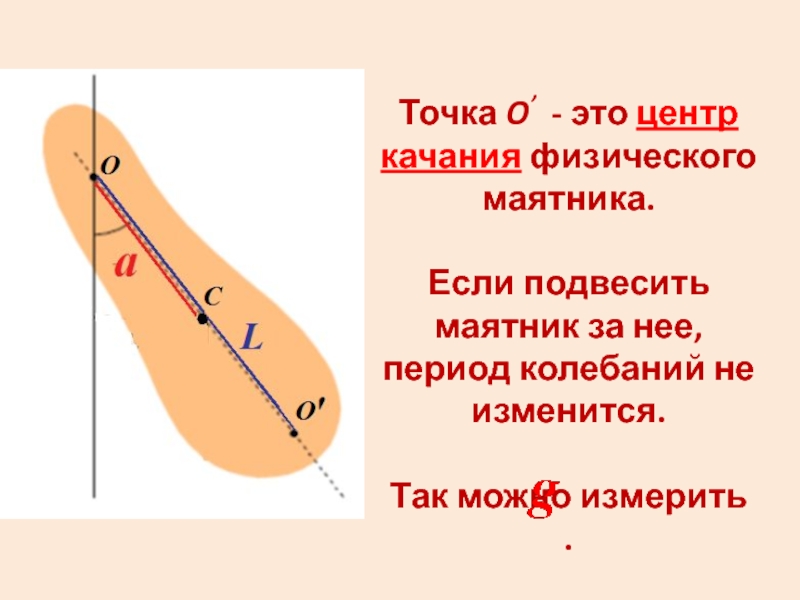
Слайд 37Точка O’ - это центр качания физического маятника.
Если подвесить
маятник за нее, период колебаний не изменится.
Так можно измерить
.
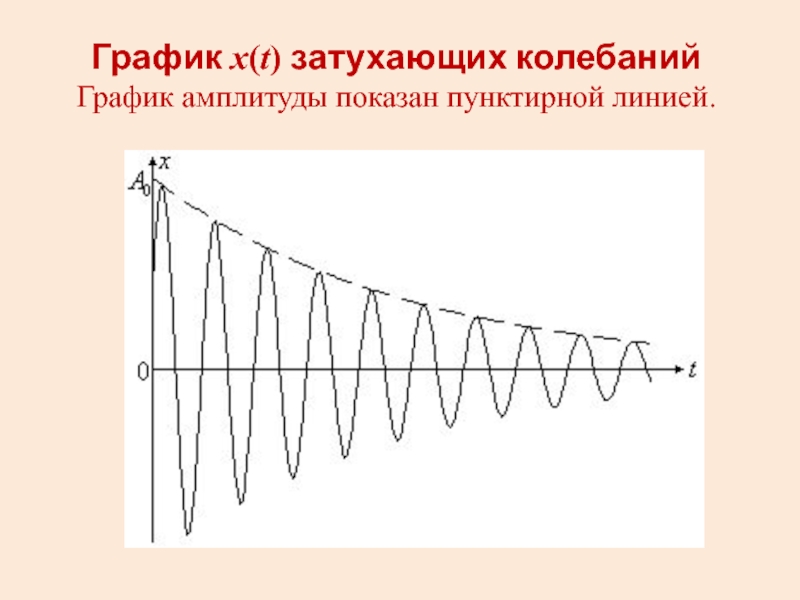
Слайд 38Затухающие колебания
Уравнение затухающих колебаний
Пусть на маятник массы m кроме
квазиупругой силы
действует сила сопротивления, — коэффициент сопротивления.
Тогда
Слайд 39 b — коэффициент затухания,
w0 — собственная
циклическая частота.
Уравнение движения принимает вид:
Это дифференциальное уравнение затухающих колебаний
Делим на массу:
Обозначим:
Слайд 40
A0 - начальная амплитуда,
- начальная фаза колебаний,
- циклическая
частота затухающих колебаний:
амплитуда затухающих колебаний
При его решение:
Слайд 42
Характеристики затухания
Время релаксации t — время, за которое амплитуда
колебаний уменьшается в e раз.
или
Слайд 432. Логарифмический декремент затухания - натуральный логарифм отношения амплитуд,
взятых через период.
число колеба-ний за время
Слайд 45При большом затухании
система совершает апериодическое движение: выведенная из положения равновесия, она возвращается
в него, не совершая колебаний.Слайд 47Добавим в уравнение движения периоди-ческую силу
.
амплитуда,
циклическая частота
внешнего воздействия
квазиупругая сила
сила сопро-тивления
внешняя сила
Слайд 49Установившиеся вынужденные колебания - это гармонические колебания с частотой равной
частоте вынуждающей силы w .
Амплитуда вынужденных колебаний:
Она зависит
от амплитуды вынуждающей силы и от частоты ее колебаний w . Слайд 50Как А зависит от ?
Пусть нет затухания и =
0.
Амплитуда колебаний неограниченно возрастает при
Слайд 51Если есть затухание (всегда), то ампли-туда колебаний резко возрастает при
некоторой частоте внешнего воздейст-вия, уже не равной
.Это явление называют резонансом.