Кривые поверхности

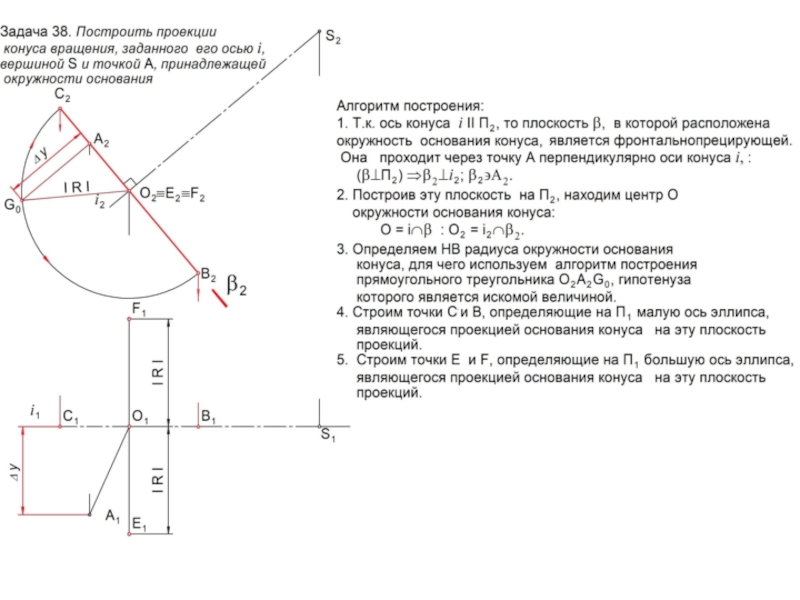
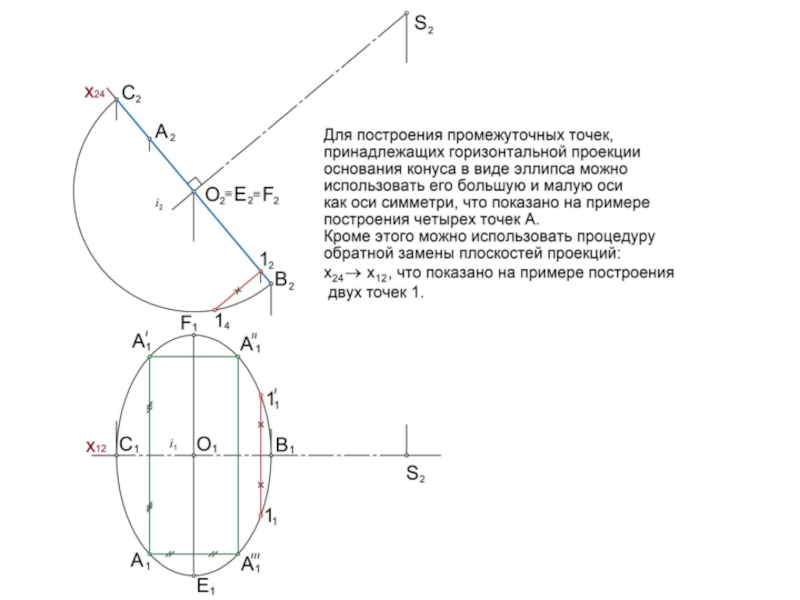
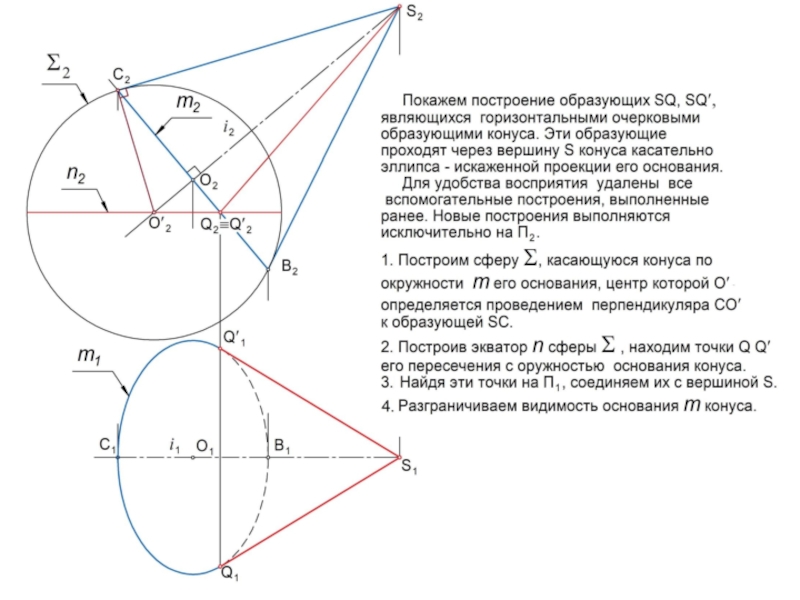
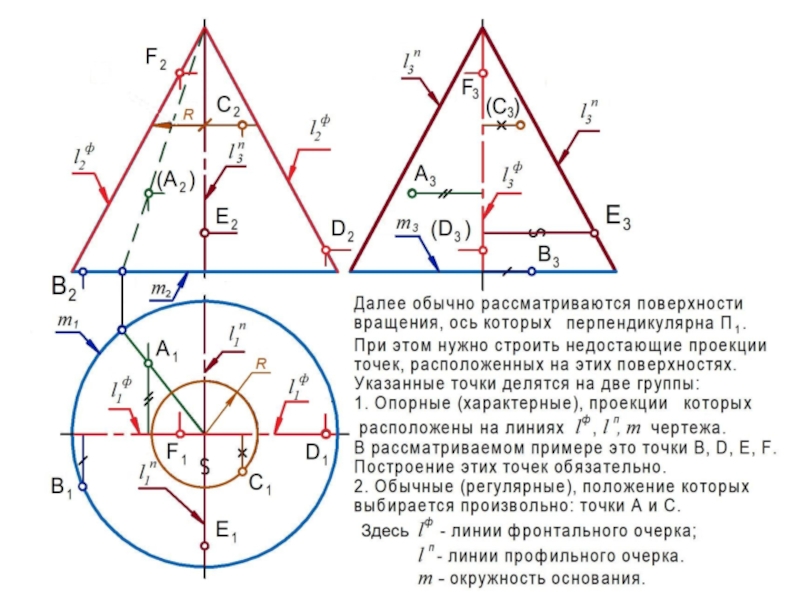
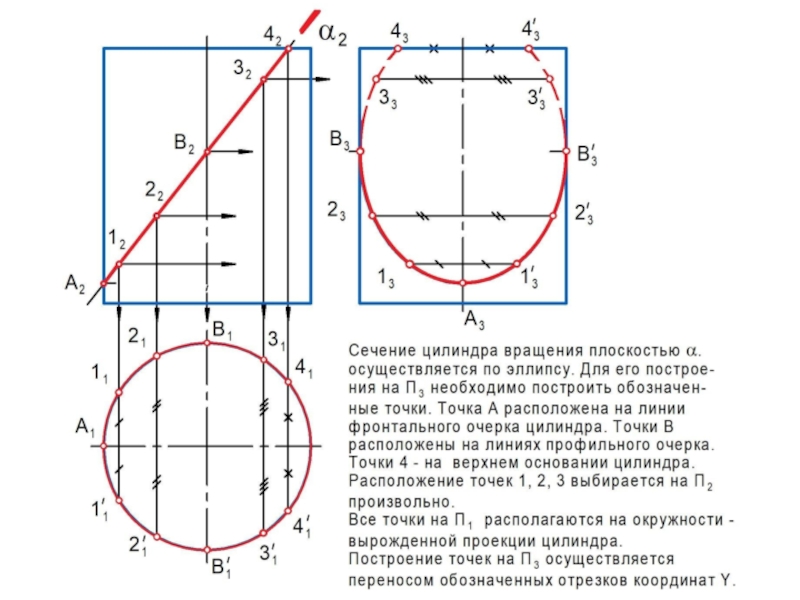
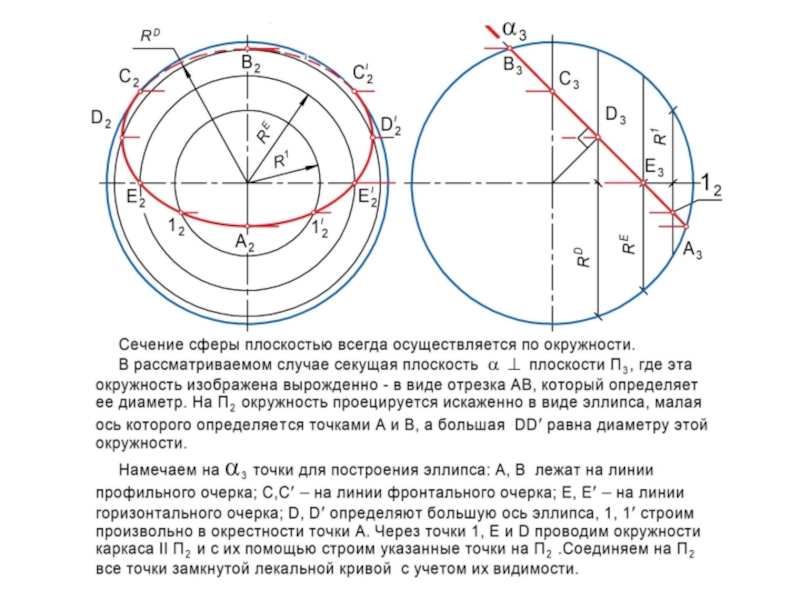
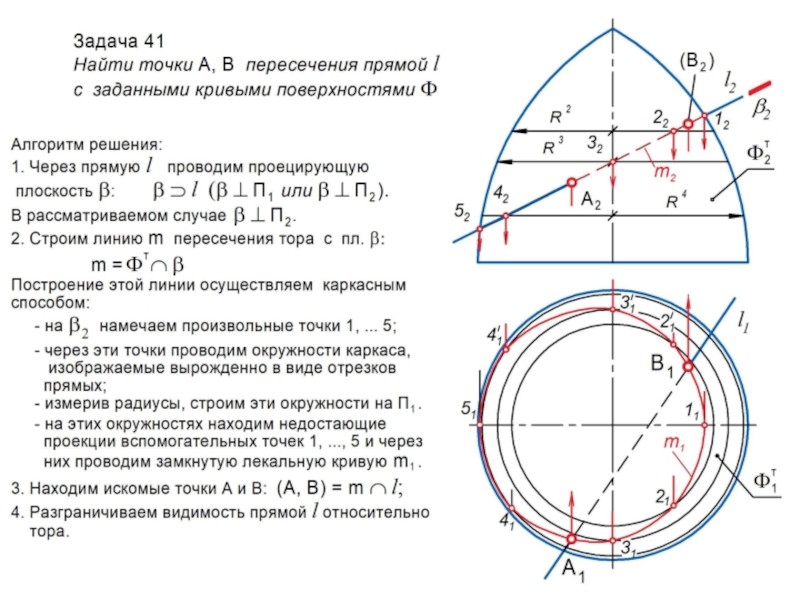
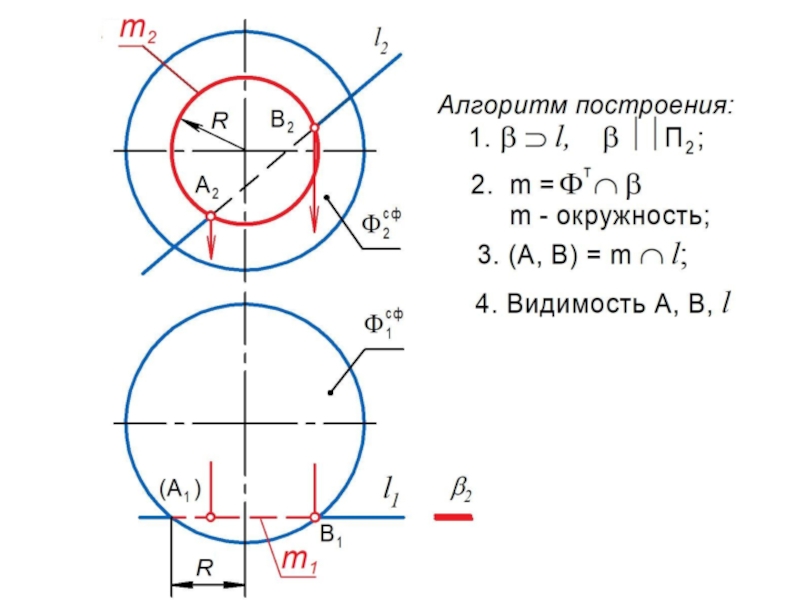
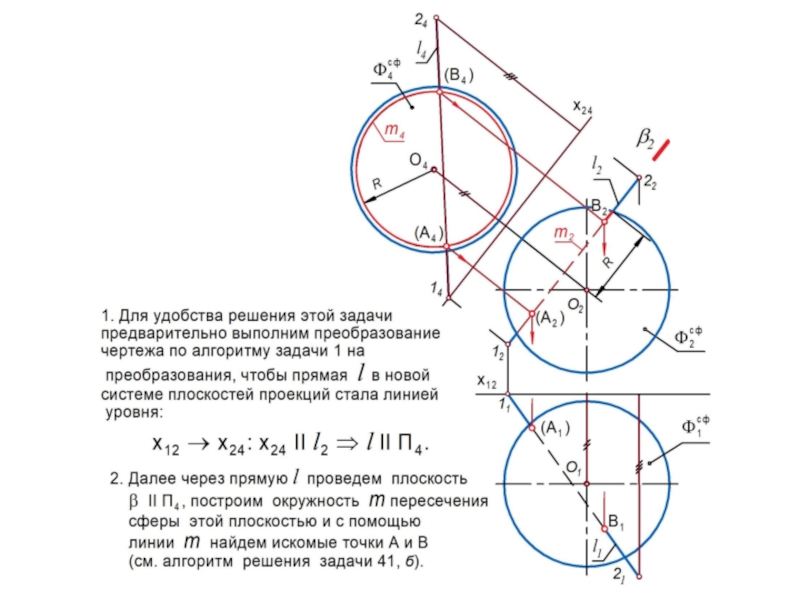
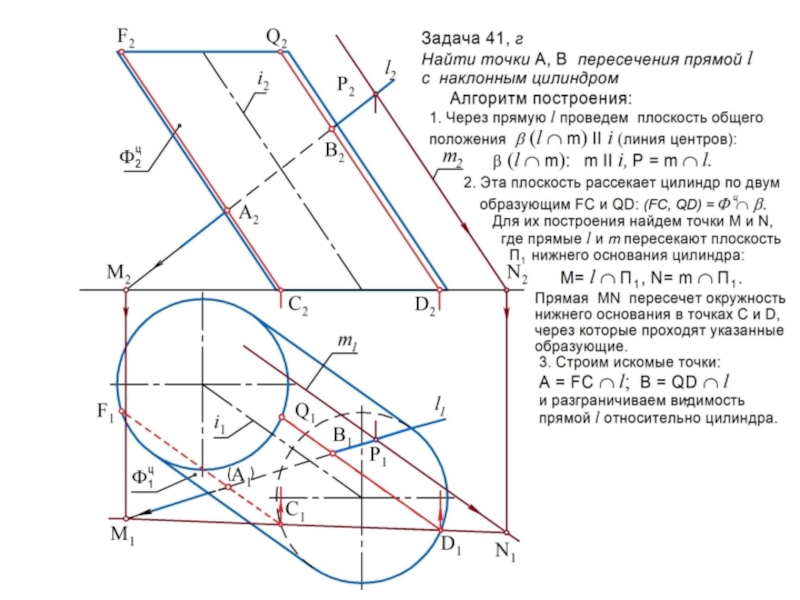
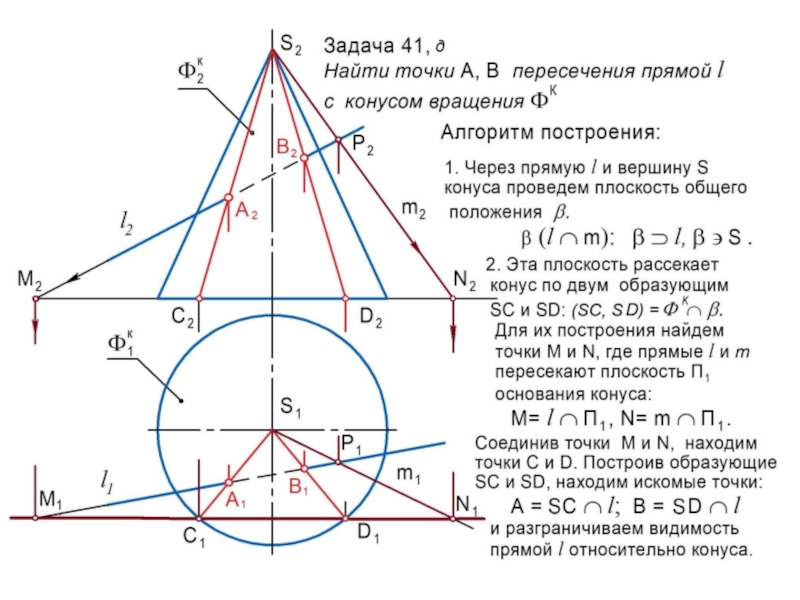
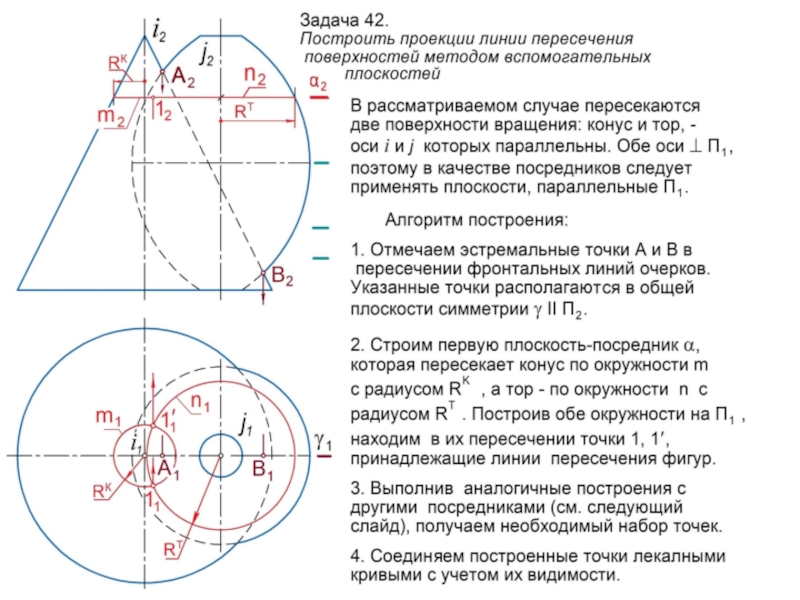
линии l или поверхности , которые называются образующими.
Наибольшее распространение среди

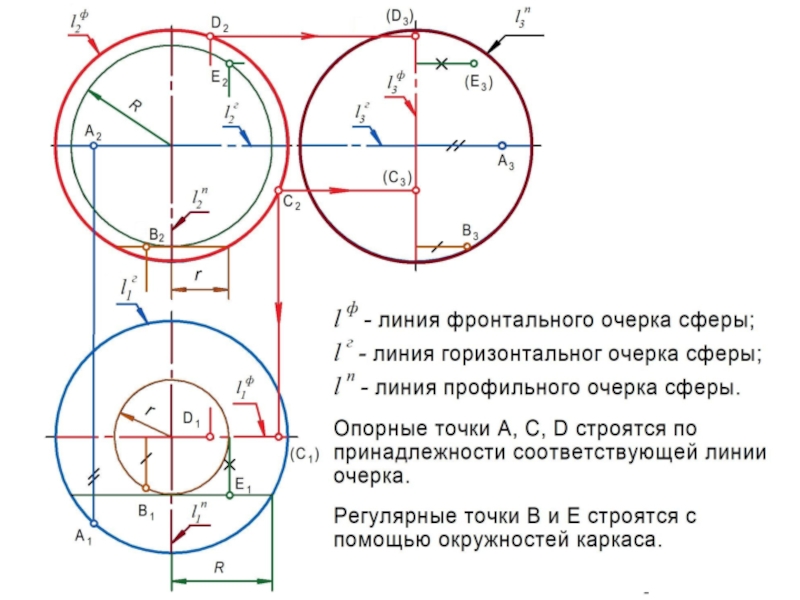
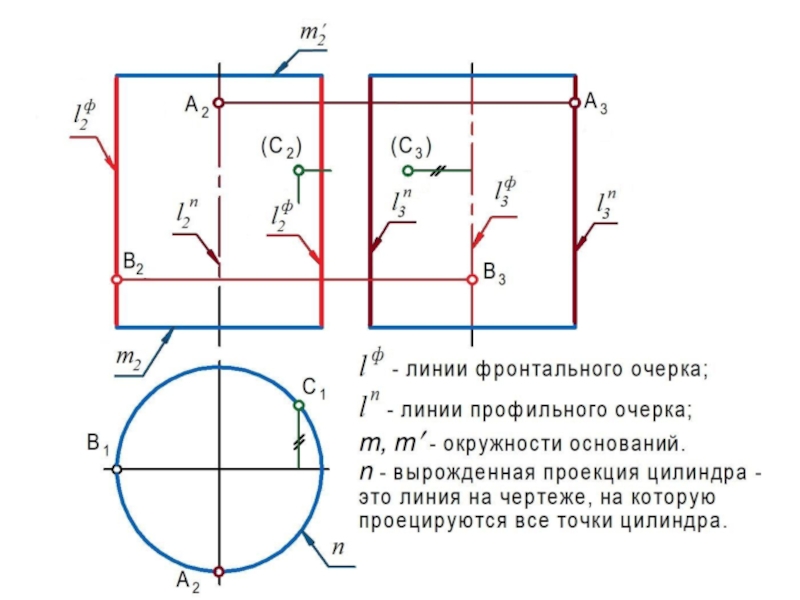
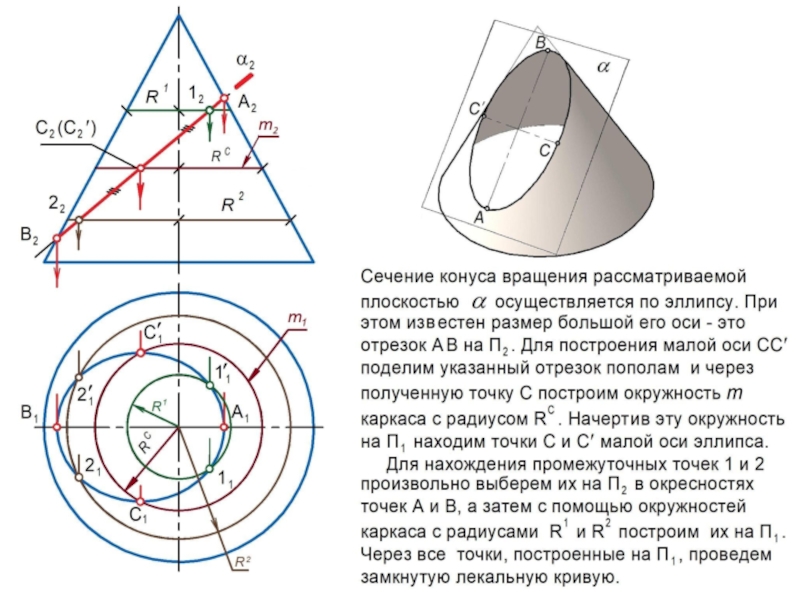
них получили поверхности вращения: цилиндр, конус, сфера, тор, эллипсоид и др., образующиеся вращением вокруг неподвижной оси линии l или поверхности  .
Для решения позиционных задач на кривых поверхностях применяется каркасный способ.
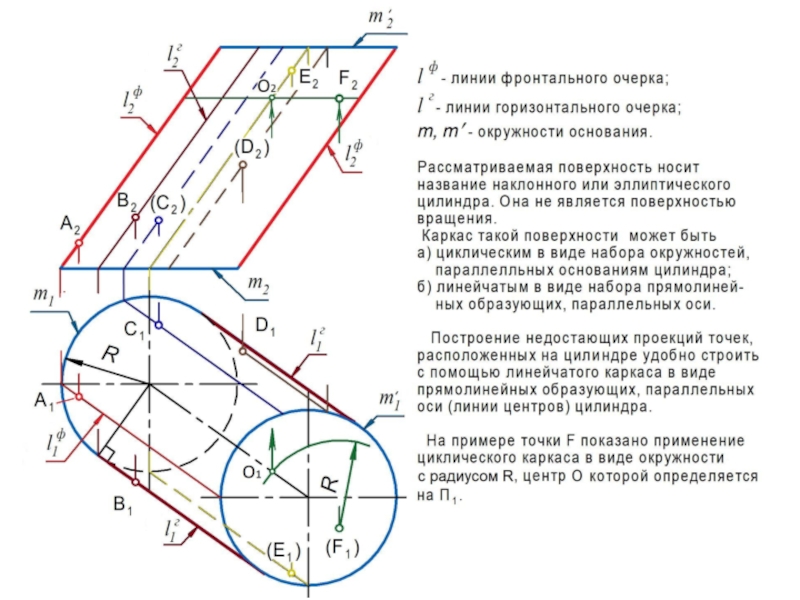
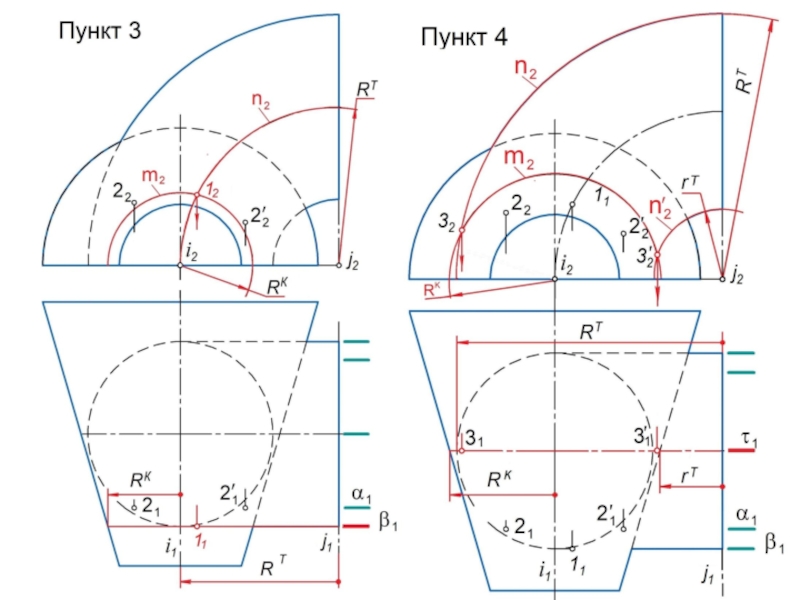
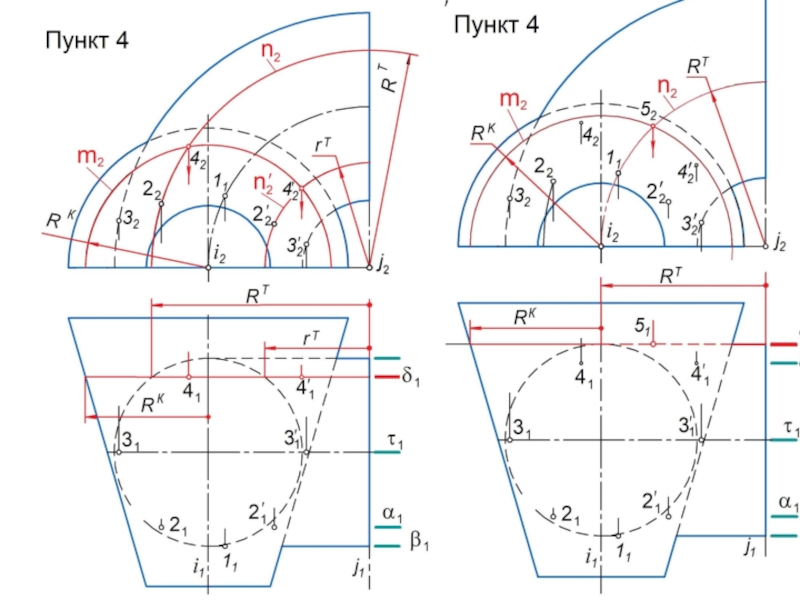
Каркасом поверхности называется совокупность линий, таким образом ее заполняющих, что в общем случае через любую точку поверхности проходит единственная линия каркаса.
При решении задач на поверхностях вращения используют каркасы:
а) линейчатый - совокупность прямых линий, заполняющих поверхность;
б) циклический – совокупность окружностей , заполняющих поверхность.
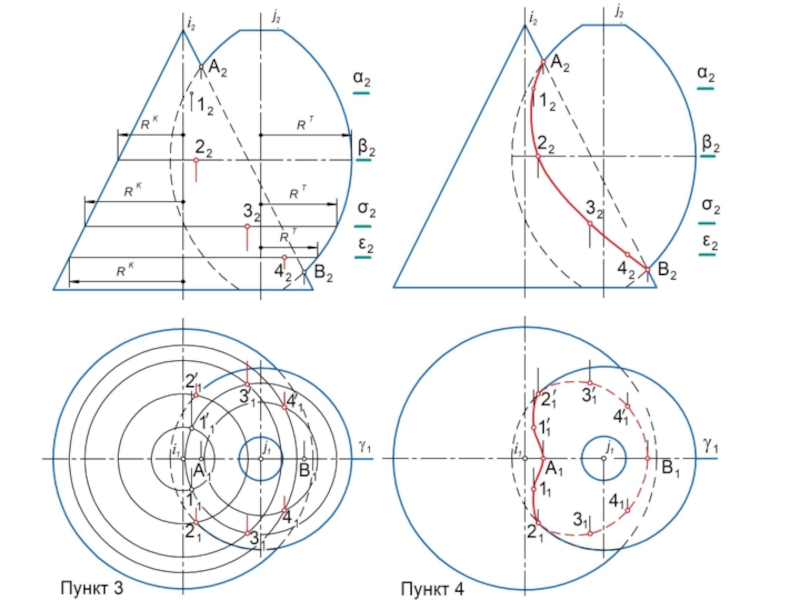
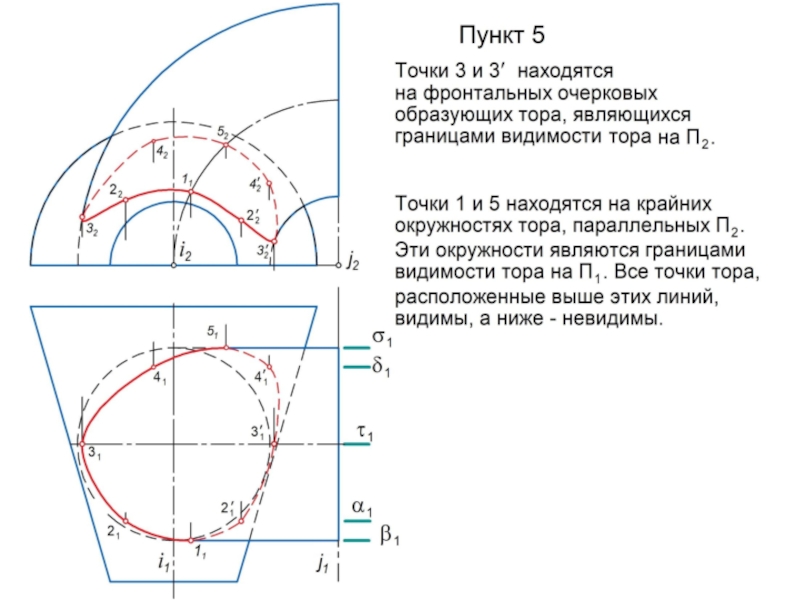
Очерком (очертанием) кривой поверхности является совокупность
линий, образующихся в результате пересечения с плоскостью проекций проецирующих поверхностей, построенных касательно заданной
поверхности.

 и  .
Необходимо построить линию

l их пересечения.
Обычно решение поставленной задачи начинается с построения опорных (характерных) точек этой линии.
К таким точкам относятся:
экстремальные, лежащие в общей плоскости симметрии пересекающихся поверхностей. Здесь экстремум означает min или max удаления точек от плоскостей проекций;
принадлежащие очерковым образующим заданных
поверхностей и определяющие видимость линии l.
Далее строится набор промежуточных (регулярных) точек, необходимых для плавного соединения точек линии l. При этом используется следующий алгоритм:
Строят поверхность-посредник , которая должна пересекать заданные поверхности по простейшим линиям каркаса (прямым или окружностям).

=    .
3. Строят линию n пересечения поверхностей

 и  : n =    .
4. Строят точки 1, 2, … пересечения линий m и n : (1, 2, …) = m  n .
Эти точки принадлежат искомой линии l.
5. Изменяют положение или размеры поверхности-посредника  и
повторяют п. п. 2 … 5 алгоритма.
6. Построив необходимое количество промежуточных точек,
последовательно соединяют все точки плавной лекальной кривой с
учетом их видимости.
В зависимости от вида поверхности-посредника  различают два
метода решения задачи на пересечение поверхностей:
1) метод вспомогательных плоскостей, если посредник  – это
плоскость;
2) метод вспомогательных сфер, если посредник  – это сфера.