Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ ГИДРОГАЗОДИНАМИКА
Содержание
- 1. КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ ГИДРОГАЗОДИНАМИКА
- 2. Чтобы описать движение жидкости, мы должны задать
- 3. Рассмотрим случай, когда нет Магнитного поля; Проводимости;Температура
- 4. Общая теория движения жидкостей будет описываться следующей
- 5. Приняв выше, что жидкость является несжимаемой, мы
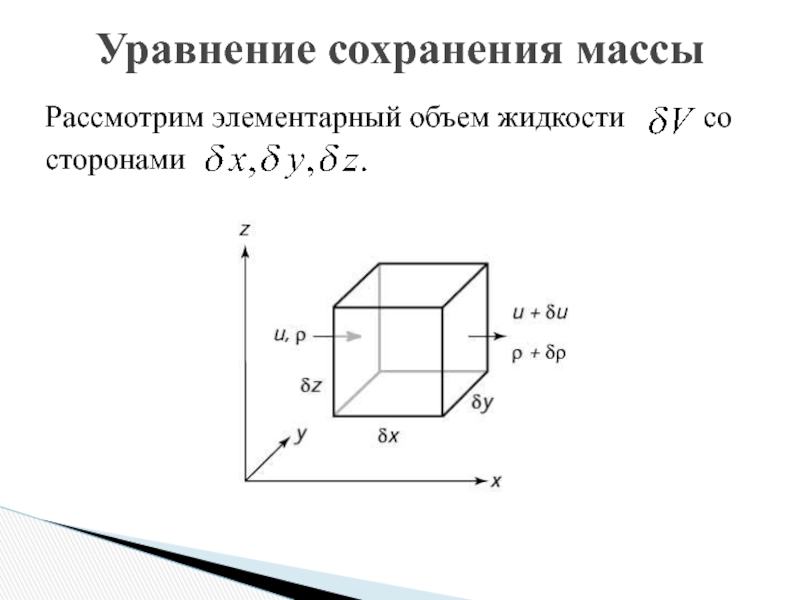
- 6. Уравнение сохранения массыРассмотрим элементарный объем жидкости состоронами
- 7. Уравнение сохранения массы
- 8. Уравнение сохранения массы
- 9. Уравнение сохранения массы
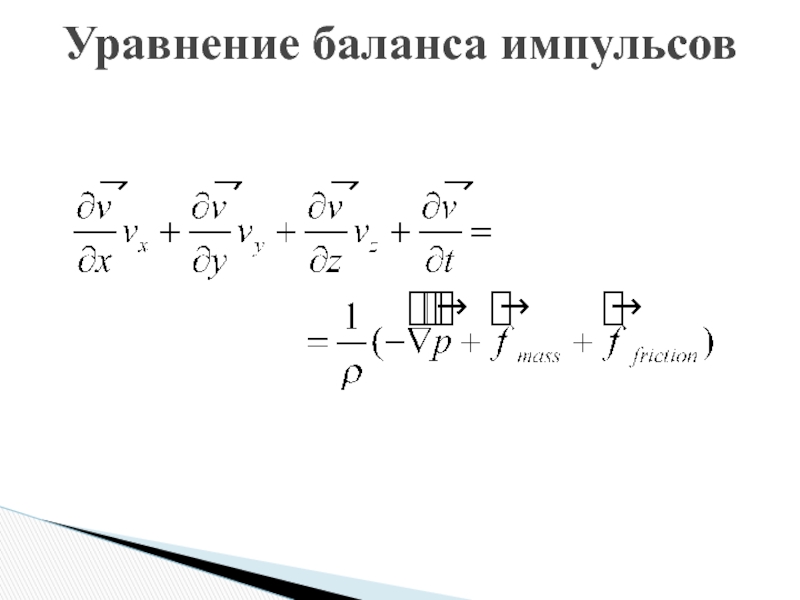
- 10. Уравнение баланса импульсов
- 11. Ускорение жидкостиВ уравнениинам известно все кроме ускорения.
- 12. Ускорение жидкостиПредставьте, что мы пометили одну капельку
- 13. Ускорение жидкостиФактически в направлении оси х она
- 14. Ускорение жидкостиВ уравнениинам известно все кроме ускорения.
- 15. Уравнение баланса импульсов
- 16. Скачать презентанцию
Чтобы описать движение жидкости, мы должны задать в каждой точке ее некие свойства. Скорость; Давление; Температура; Магнитное поле и т. д. Число полей, необходимых для полного описания ситуации, зависит от сложности
Слайды и текст этой презентации
Слайд 1КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ ГИДРОГАЗОДИНАМИКА
Лекция 2
ОСНОВЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
(Часть 2
– Движение жидкости)
Слайд 2Чтобы описать движение жидкости, мы должны задать в каждой точке
ее некие свойства.
Скорость;
Давление;
Температура;
Магнитное поле и т.
д. Число полей, необходимых для полного описания ситуации, зависит от сложности задачи.
Описание движения жидкости
Слайд 3Рассмотрим случай, когда нет
Магнитного поля;
Проводимости;
Температура считается постоянной.
Фактически мы
уменьшим сложность нашей работы, допустив, что плотность постоянна, т. е.
что жидкость существенно несжижаема.Основные допущния
Слайд 4Общая теория движения жидкостей будет описываться следующей системой уравнений:
Уравнение
состояния;
Уравнение сохранения массы;
Уравнение баланса импульсов;
Уравнение сохранения энергии.
Общая
теория движения ждкостейСлайд 5Приняв выше, что жидкость является несжимаемой, мы определили уравнение состояния
в виде
Уравнение состояния
Легко определить, когда такое предположение о постоянстве
будет хорошим: если скорость потока гораздо меньше скорости звуковой волны, то нам не нужно заботиться об изменениях плотности.Слайд 11Ускорение жидкости
В уравнении
нам известно все
кроме ускорения. Самым простым было
бы предположение, что ускорение равно
, однако это совсем неверно.Производная выражает изменение скорости v в фиксированной точке пространства.
Слайд 12Ускорение жидкости
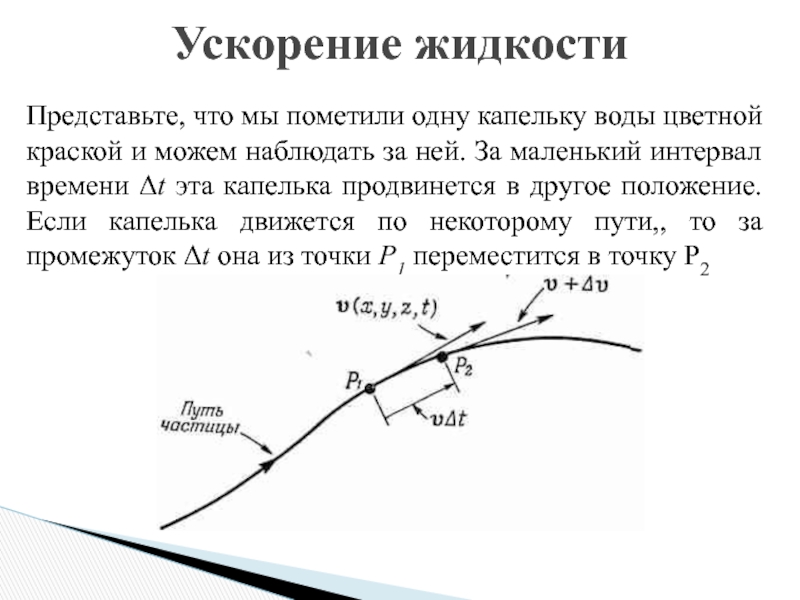
Представьте, что мы пометили одну капельку воды цветной краской
и можем наблюдать за ней. За маленький интервал времени t
эта капелька продвинется в другое положение. Если капелька движется по некоторому пути,, то за промежуток t она из точки Р1 переместится в точку Р2Слайд 13Ускорение жидкости
Фактически в направлении оси х она передвинется на расстояние
vxt, в направлении оси у на расстояние vуt, а в
направлении оси z — на расстояние vzt. Мы видим, что если — скорость частицы в момент t, то скорость той же самой частицы в момент t+t представляет величинуТогда имеем:
Слайд 14Ускорение жидкости
В уравнении
нам известно все
кроме ускорения. Самым простым было
бы предположение, что ускорение равно
, однако это совсем неверно.Производная выражает изменение скорости v в фиксированной точке пространства.