Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КУРС ЛЕКЦИЙ МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ В ГЕОЛОГИИ Курамшин Ринат
Содержание
- 1. КУРС ЛЕКЦИЙ МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ В ГЕОЛОГИИ Курамшин Ринат
- 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕПРОСТРАНСТВЕННЫХГЕОЛОГИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ
- 3. СВОЙСТВА ГЕОЛОГИЧЕСКИХОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕПЕРЕМЕННЫЕ
- 4. СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕРассмотрим и
- 5. Рассмотрим параметры геометрии сети наблюдений и области
- 6. Равномерная сеть характеризуется постоянным шагом h –
- 7. Плотность сети – количество наблюдений на единицу
- 8. Размер области наблюдения влияет на некоторые характеристики.ПРИМЕР:
- 9. Результаты измерений пространственных переменных сводят в матрицу,
- 10. ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
- 11. Математическое моделирование геологического объекта ставит своей целью
- 12. В детерминированных моделях предполагается, что пространственная переменная
- 13. Случайные функции основаны на предположении о том,
- 14. Геостатистические модели содержат предположение о том, что
- 15. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
- 16. Линейная интерполяционная модельПолиномиальная модельМодель обратных расстоянийСплайн-модельДетерминированные модели геологических объектов бывают следующих видов: ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
- 17. В основе модели лежит предположение о том,
- 18. Линейную интерполяцию можно представить графически в виде
- 19. Линейная интерполяция может быть выполнена и в
- 20. Следует отметить, что линейная интерполяционная модель, как
- 21. В основе модели лежит предположение о том,
- 22. В основу модели положена идея о том,
- 23. Сплайн – это кусочно-непрерывная гладкая функция, состоящая
- 24. В каждом полиноме четыре неизвестных коэффициента a,
- 25. Нахождение коэффициентов a, b, с, d сводится
- 26. В n – 2 пунктах стыковки должны быть равны
- 27. Могут быть заданы и другие условия, например
- 28. Для уменьшения объема вычислений, рекомендуется применять скользящий
- 29. Более сложным является расчет двухмерного сплайна. В
- 30. ВЕРОЯТНОСТНЫЕ МОДЕЛИГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
- 31. ВЕРОЯТНОСТНЫЕ МОДЕЛИ МОДЕЛИ ГЕОЛОГИЧЕСКИХ ПОЛЕЙМодель на основе
- 32. Основой случайной функции служит предположение, что измеренные
- 33. График случайной функцииМОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИСлучайную
- 34. Случайная функция имеет три главные характеристики: математическое
- 35. Математическое ожидание стационарной случайной функции величина постоянная
- 36. Дисперсия случайной функции равна дисперсии отклонений (х):Если из
- 37. Она является аналогом коэффициента корреляции случайных величин,
- 38. Идеальная форма автокорреляционной функцииМОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 39. Следует отметить, что шаг и радиус автокорреляции
- 40. Изучение нестационарной случайной функции начинается с выделения
- 41. ПРИМЕР. Имеются результаты измерения переменной (табл.). Требуется
- 42. После вычитания из исходных данных полинома получим
- 43. На практике часто используют двухмерный (площадной) тренд,
- 44. Существует много способов сглаживания. Наиболее часто сглаживание
- 45. В составе закономерной изменчивости часто присутствует
- 46. Каждая синусоида имеет три характеристики: ГАРМОНИЧЕСКИЙ АНАЛИЗ
- 47. В качестве первой длины волны L чаще
- 48. Количество гармоник N может быть большим, но
- 49. Объединение формул ряда значений пространственной переменной f(x)
- 50. Амплитуды гармоник (Ak) вычисляют когда определены коэффициенты
- 51. Периодическая изменчивость не обязательно должна быть синусоидальной,
- 52. ОСНОВЫ ГЕОСТАТИСТИКИ
- 53. ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИВ основе геостатистической группы
- 54. ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИγ(h) + K(h) = D. На основе гипотезы
- 55. ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИДля непрерывных пространственных переменных
- 56. ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИДля дискретных пространственных переменных
- 57. Вариограмма имеет радиус влияния R, который идентичен
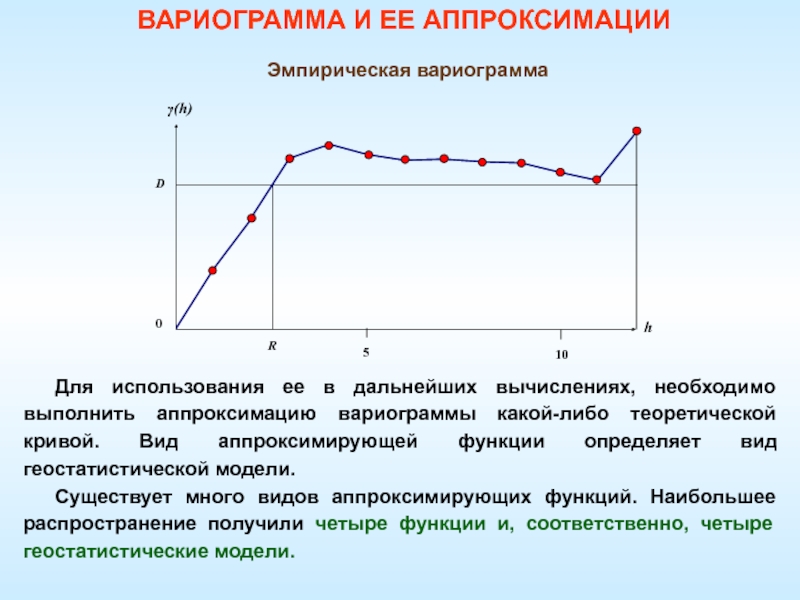
- 58. Эмпирическая вариограммаВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИДля использования ее
- 59. Линейная модель вариограммыПервая модель линейная. В ней
- 60. Полиномиальная модель вариограммыВо второй модели вариограмма аппроксимируется
- 61. Третья модель (сферическая) также аппроксимируется кубическим полиномом,
- 62. Модель Де-ВийсаЧетвертая модель (модель Де-Вийса) характеризуется тем,
- 63. Выбор варианта аппроксимации носит произвольный характер. Наилучшим
- 64. Многие характеристики пространственной переменной зависят от геометрической
- 65. Пусть в геологическом объекте имеется множество точек,
- 66. При увеличении размеров геометрической базы происходит усреднение
- 67. Изменение дисперсии по мере увеличения объема v
- 68. Подобные формулы существуют и для вариограммы:или в
- 69. где k(х) = 1, когда точка х находится внутри
- 70. Геометрический смысл ковариограммы заключается в степени перекрытия
- 71. На основе геостатистических моделей создан новый метод
- 72. Схема точечного кригингаПОНЯТИЕ О КРИГИНГЕПусть имеется область
- 73. ПОНЯТИЕ О КРИГИНГЕгеологический объект изотропный, тогда вокруг
- 74. Прогнозное значение находится в результате выполнения ряда
- 75. 5. Решение системы дает весовые коэффициенты p1,
- 76. При необходимости вычисления прогнозного значения в следующем
- 77. У точечного кригинга имеется один недостаток –
- 78. ПОНЯТИЕ О КРИГИНГЕВ качестве тренда используется аппроксимирующий
- 79. Задание к семинару (группам ГГ-07-8, ГР-07-2 к 29.03.11): РЕШИТЬ ЗАДАНИЯ №9,10,11
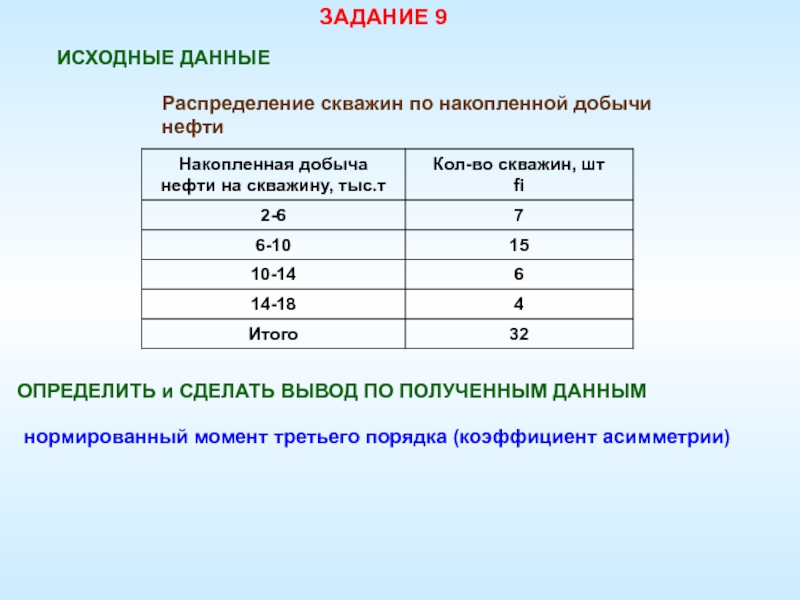
- 80. ЗАДАНИЕ 9ИСХОДНЫЕ ДАННЫЕРаспределение скважин по накопленной добычи
- 81. ЗАДАНИЕ 10ИСХОДНЫЕ ДАННЫЕОПРЕДЕЛИТЬ и СДЕЛАТЬ ВЫВОД ПО
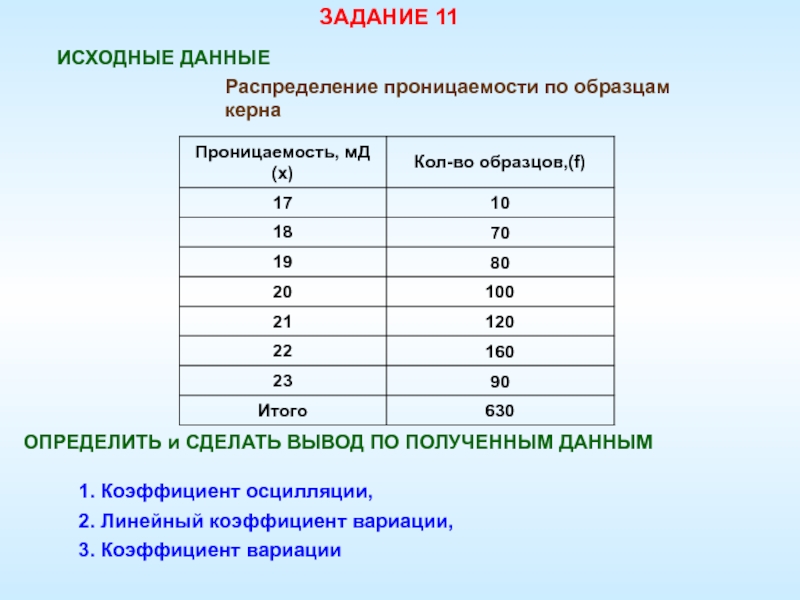
- 82. ЗАДАНИЕ 11ИСХОДНЫЕ ДАННЫЕОПРЕДЕЛИТЬ и СДЕЛАТЬ ВЫВОД ПО
- 83. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1КУРС ЛЕКЦИЙ
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ В ГЕОЛОГИИ
Курамшин Ринат Мунирович
кандидат технических наук,
доцент
кафедры,
Слайд 4СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕ
Рассмотрим и изучим свойства объектов
как функции координат пространства – пространственные переменные.
В роли пространственных
переменных могут выступать мощность отложений песчаных тел, абсолютные отметки кровли и подошвы пласта, изменение пористости и многие другие величины.Пространство, в котором существует изучаемая величина, называется геологическим телом пространственной переменной. В каждой точке или области геологического тела с координатами x, у, z свойство принимает конкретное значение (x, у, z ). В каждой точке или области геологического тела могут быть измерены несколько величин.
Значения пространственной переменной измеряют в пределах геологических объектов конечных размеров по какой-то сети в ограниченных областях геологического тела.
Слайд 5Рассмотрим параметры геометрии сети наблюдений и области измерений.
Геометрия сети
наблюдений характеризуется формой, расположением и плотностью сети.
Сеть бывает одномерная
– вдоль линии, двухмерная – по площади и трехмерная – в объеме геологического тела. Измерения делят на непрерывные и дискретные (прерывистые).
Для математической обработки непрерывные измерения обычно преобразуют в дискретные.
Наблюдения могут размещаться по равномерной, кратной или неравномерной сети.
СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕ
Слайд 6
Равномерная сеть характеризуется постоянным шагом h – равным расстоянием между
пунктами наблюдений.
В двухмерной сети имеется два постоянных шага h1
и h2, которые образуют ячейку сети площадью s = h1h2. Если h1 = h2, то сеть квадратная. Трехмерная сеть имеет три постоянных шага h1, h2, h3, образующих ячейку объемом v = h1h2h3.
В реальных условиях не всегда удается соблюдать строго равномерную сеть наблюдений. Небольшими отклонениями от равномерной сети часто можно пренебречь.
У кратной сети расстояния между пунктами наблюдений непостоянные, но кратные шагу h.
СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕ
Слайд 7Плотность сети – количество наблюдений на единицу длины, площади или
объема геологического объекта. Если сеть наблюдений отличается от равномерной, то
можно говорить о средней плотности сети.Обычно пространственная переменная предполагается непрерывной величиной, плавно меняющей свое значение в геологическом теле. Возможны сравнительно резкие и скачкообразные изменения пространственной переменной, отражающие дискретность строения геологических объектов и позволяющие проводить внутри них геологические границы.
Геометрия области измерения характеризуется формой, размером и ориентировкой.
Форма области может быть точечной, линейной, сферической, цилиндрической и пр. Во многих случаях формой области можно пренебречь, полагая ее точечной.
СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕ
Слайд 8Размер области наблюдения влияет на некоторые характеристики.
ПРИМЕР: при увеличении размера
области уменьшается дисперсия величин. Размером области измерения также часто пренебрегают,
считая измерения точечными, тем более что размеры области обычно на порядок ниже шага сети наблюдений.При уменьшении размеров области некоторые измерения стремятся к предельному значению величины в данной точке, что характерно для непрерывных величин, например для мощности геологических тел.
В других случаях такой предел отсутствует из-за дискретности строения геологических объектов. В этих случаях принято говорить о средних значениях пространственной переменной в некоторой малой области геологического тела.
Ориентировка области измерений имеет значение для анизотропных геологических тел, а их большинство. При различной ориентировке кернового материала в анизотропной среде можно получить разные результаты.
СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕ
Слайд 9Результаты измерений пространственных переменных сводят в матрицу, в которой присутствуют
значения величины и координаты пунктов наблюдений (центров областей измерений)
х, у, z: В зависимости от количества учитываемых координат пространственные переменные и геологические тела делятся на одно-, двух- и трехмерные.
СВОЙСТВА ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ КАК ПРОСТРАНСТВЕННЫЕ ПЕРЕМЕННЫЕ
где n – количество объектов, k – количество величин.
Слайд 11Математическое моделирование геологического объекта ставит своей целью описание поведения пространственной
переменной по имеющимся результатам наблюдений, а также прогнозирование ее значений
в заданных точках или областях геологического объекта. Попутно могут быть решены задачи оценки погрешности прогнозирования, рациональной плотности сети измерений и другие.Реальные геологические объекты обладают большой сложностью. Математические модели геологических объектов не позволяют дать их исчерпывающую характеристику, а отражают лишь наиболее существенные черты. Для каждого геологического объекта можно построить много математических моделей, различающихся характером предположений о поведении величин в пространстве.
Математические модели геологических объектов делятся на детерминированные и вероятностные.
ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
Слайд 12В детерминированных моделях предполагается, что пространственная переменная является неслучайной функцией
координат и однозначно зависит от местоположения пунктов измерений.
В тех
пунктах, где проводились измерения, значения пространственной переменной принимают фактическими, а в промежутках между ними находят путем интерполяции. Способ интерполяции определяет вид математической модели. Среди детерминированных моделей можно выделить модели линейные, полиномиальные, обратных расстояний и сплайн-модели.
В вероятностных моделях предполагается, что значения пространственной переменной (в том числе и в пунктах измерений) содержат элементы случайности.
Различают две группы математических моделей: случайные функции и геостатистические модели. В разных группах по-разному объясняется появление случайной составляющей.
ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
Слайд 13Случайные функции основаны на предположении о том, что значения пространственной
переменной (х) испытывают случайные колебания δ(х) около неслучайной составляющей, называемой
математическим ожиданием m(x):(х) = m(x) + (х).
В геологической литературе математическое ожидание называют также регулярной, координированной, закономерной составляющей или трендом.
Математическое ожидание иногда делят на регулярную f(x) и периодическую (х) составляющие:
m(x) = f(x) + (х).
Может быть несколько периодических составляющих, различающихся амплитудой и длиной волны.
ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
Слайд 14Геостатистические модели содержат предположение о том, что случайный результат измерений
вызван случайным расположением пунктов наблюдений.
Любое перемещение сети наблюдений приводит
к получению новых результатов, но при этом остается неизменным средний квадрат разности между результатами измерений в пунктах, отстоящих друг от друга на шаг h. Полусумма среднего квадрата разностей называется вариограммой γ(h)
Геостатистические модели различаются способом аппроксимации эмпирической вариограммы теоретической вариограммой и после-дующей интерполяцией результатов наблюдений.
ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
Слайд 16Линейная интерполяционная модель
Полиномиальная модель
Модель обратных расстояний
Сплайн-модель
Детерминированные модели геологических объектов бывают
следующих видов:
ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ
ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ
Слайд 17В основе модели лежит предположение о том, что между пунктами
измерений значения пространственной переменной меняются по закону прямой линии.
При
густой сети измерений и слабой изменчивости величин предположение может быть близким к действительности и не повлечет за собой существенных погрешностей при прогнозировании значений между пунктами измерений. Может быть противоположная ситуация, когда величина настолько изменчива, что какое-нибудь разумное предположение о ее поведении между пунктами измерений сделать невозможно.
В этом случае линейная модель выбирается из соображений максимальной простоты, что обеспечивает высокую достоверность прогнозирования.
Подобные соображения используют, например, для оконтуривания залежи при подсчете запасов.
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИОННАЯ МОДЕЛЬ
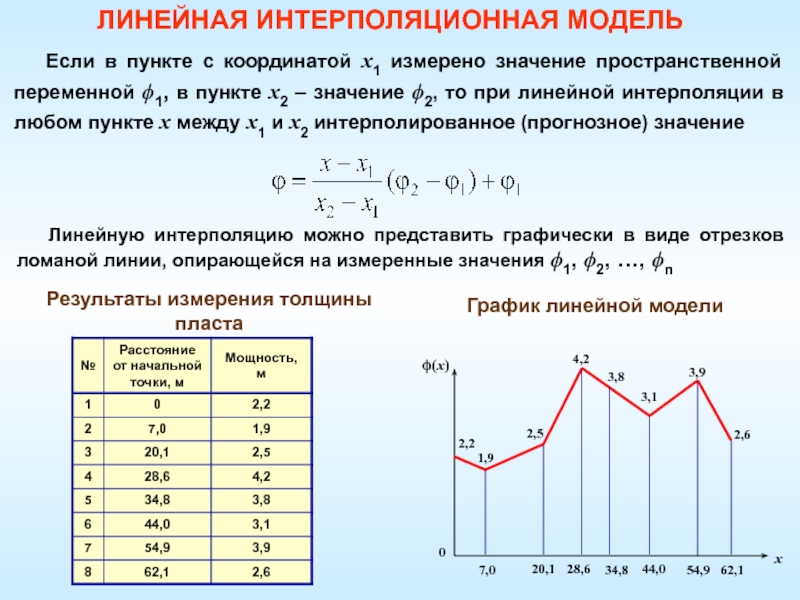
Слайд 18Линейную интерполяцию можно представить графически в виде отрезков ломаной линии,
опирающейся на измеренные значения 1, 2, …, n
График линейной модели
Результаты
измерения толщины пласта
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИОННАЯ МОДЕЛЬ
Если в пункте с координатой х1 измерено значение пространственной переменной 1, в пункте х2 – значение 2, то при линейной интерполяции в любом пункте х между х1 и х2 интерполированное (прогнозное) значение
Слайд 19Линейная интерполяция может быть выполнена и в двухмерном пространстве внутри
треугольника, образованного тремя пунктами наблюдений, не лежащими на одной прямой.
По данным в вершинах треугольника можно найти уравнение плоскости:
= ах + by + c.
Уравнение позволяет вычислять интерполированное значение в любой точке с заданными координатами х и у внутри треугольника.
Если имеется много пунктов наблюдений, то охваченная ими площадь разбивается на несколько треугольников и в каждом из них рассчитывается свое интерполяционное уравнение.
Можно распространить линейную интерполяцию и на трехмерное пространство, которое разделяется на совокупность тетраэдров.
Каждый тетраэдр образован четырьмя пунктами измерений, не лежащими на одной плоскости.
Внутри тетраэдра интерполяция осуществляется с помощью уравнения (гиперплоскости) которое опирается на вершины тетраэдра.
= ах + by + cz + d
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИОННАЯ МОДЕЛЬ
Слайд 20Следует отметить, что линейная интерполяционная модель, как и другие детерминированные
модели, не позволяет оценить погрешность интерполяции без привлечения дополнительных данных.
Чтобы решить эту задачу, надо выполнить дополнительные измерения пространственной переменной внутри интервалов интерполяции и сравнить интерполированные и измеренные данные.
Статистическая обработка таких материалов позволяет выявить, как погрешность интерполяции зависит от расстояния между пунктами наблюдений.
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИОННАЯ МОДЕЛЬ
Слайд 21В основе модели лежит предположение о том, что поведение пространственной
переменной нелинейное и может быть описано полиномиальной функцией, значения которой
совпадают с фактическими данными в пунктах измерений.Полиномиальная функция может быть одно-, двух- и трехмерной. Простейшая одномерная полиномиальная функция имеет вид
ПОЛИНОМИАЛЬНАЯ МОДЕЛЬ
(х) = a0 + a1x + a2x2 + … + akxk.
Порядок полинома k на единицу меньше числа измерений n.
Полиномиальная модель редко применяется на практике, так как по мере увеличения числа измерений степень полинома растет, а при высоких степенях полинома интерполированные значения вычисляются с большой погрешностью и испытывают столь сильные изменения, что часто переходят границы реальности.
Слайд 22В основу модели положена идея о том, что влияние измерений
убывает обратно пропорционально квадрату расстояния r от пункта измерения (как
в законе всемирного тяготения или в электрическом поле заряженных частиц), поэтому модель часто называют потенциальной.Интерполированное значение в каждой точке находят как средневзвешенное из измеренных значений в соседних пунктах n:
МОДЕЛЬ ОБРАТНЫХ РАССТОЯНИЙ
Если расстояние r равно нулю, то в данном пункте принимается измеренное фактическое значение. Для прогнозирования берут три-пять ближайших пунктов измерений или ограничиваются каким-то произвольным радиусом R.
В расчет принимают все пункты измерений в пределах этого радиуса. За пределами радиуса влияние измеренных значений не учитывается.
Слайд 23Сплайн – это кусочно-непрерывная гладкая функция, состоящая из множества полиномиальных
функций третьего порядка, плавно переходящих друг в друга.
Сплайн позволяет
построить плавный график пространственной переменной, хорошо согласующийся с геологическими представлениями, и поэтому весьма популярен. Его можно уподобить гибкой упругой линейке, опирающейся на ординаты фактических значений пространственной переменной. Концы линейки могут быть свободными или закрепленными с заданным углом наклона. Сплайн бывает одно-, двух- и трехмерным. Рассмотрим методику расчета одномерного сплайна.
Пусть имеется n пунктов измерений с координатами x1, x2, …, xn. В каждом пункте измерено значение пространственной переменной 1, 2, …, n. Между пунктами измерений имеется n – 1 отрезок. Каждый отрезок представлен полиномом третьего порядка:
СПЛАЙН-МОДЕЛЬ
= а + bx + cx2 + dx3.
Слайд 24В каждом полиноме четыре неизвестных коэффициента a, b, с, d.
Следовательно, всего имеем 4(n – 1) неизвестный коэффициент.
Их нужно
подобрать такими, чтобы выполнялись следующие условия:в пунктах x1, x2, …, xn значения полиномов должны совпадать с измеренными значениями 1, 2, …, n;
в пунктах стыковки соседних полиномов x1, x2, …, xn-1 не должно быть изломов, т.е. наклоны линий должны быть одинаковыми, что сводится к равенству первых производных от полиномов;
в тех же пунктах стыковки не должно быть скачка кривизны, что соответствует равенству вторых производных от полиномов;
в начальном и конечном пунктах должны быть заданы граничные условия.
СПЛАЙН-МОДЕЛЬ
Слайд 25Нахождение коэффициентов a, b, с, d сводится к решению системы
4(n – 1) уравнения первой
степени, которые получаются следующим образом.Каждое значение полинома должно совпадать с левым измеренным значением каждого отрезка пространственной переменной, что дает n – 1 уравнение:
Каждое значение полинома должно совпадать с правым измеренным значением каждого отрезка пространственной переменной, что дает еще n – 1 уравнение:
СПЛАЙН-МОДЕЛЬ
Слайд 26В n – 2 пунктах стыковки должны быть равны первые производные соседних
полиномов ( = b + 2cx + 3dx2) – равенство касательных:
СПЛАЙН-МОДЕЛЬ
В тех же n – 2 пунктах стыковки
должны быть равны вторые производные соседних полиномов ( = 2с + 6dx) – равенство кривизны:Слайд 27Могут быть заданы и другие условия, например наклон касательной (т.е.
первой производной) в крайних пунктах.
В результате получится необходимое число уравнений
4(n – 1). Решение системы уравнений дает все необходимые коэффициенты полиномов, что позволяет прогнозировать значения пространственной переменной между пунктами измерений.
При большом числе пунктов измерений получается довольно громоздкая система уравнений первой степени, и, хотя ее решение на компьютере не составляет труда, объем вычислений довольно значителен.
СПЛАЙН-МОДЕЛЬ
Нужны еще два уравнения, учитывающие граничные условия в конечных пунктах х1 и хn. Чаще других применяется условие, что в конечных пунктах кривизна нулевая (концы упругой линейки не закреплены), т.е. вторые производные должны быть нулевыми:
Слайд 28Для уменьшения объема вычислений, рекомендуется применять скользящий сплайн.
Для скользящего
сплайна берут четыре или шесть смежных пунктов измерений, по ним
рассчитывают уравнения сплайна, а для построения и прогнозирования выбирают один полином, занимающий среднее положение.Потом осуществляется перемещение на один пункт измерения (скольжение) и расчет повторяется. Эти операции доводят до конечного пункта измерений.
Исключение делается для первого отрезка, для которого используют первое уравнение, и для последнего отрезка, для которого используют последнее уравнение.
СПЛАЙН-МОДЕЛЬ
Слайд 29Более сложным является расчет двухмерного сплайна.
В литературе не удалось
найти полное решение двухмерного сплайна для произвольно расположенных пунктов измерений.
Имеющиеся публикации рассчитаны только на прямоугольную сеть, причем вычисляются сплайны в двух перпендикулярных направлениях, а в промежутках между ними используется интерполяция.
Теоретически можно построить и трехмерный сплайн, но на практике его, по-видимому, не применяют.
СПЛАЙН-МОДЕЛЬ
Слайд 31ВЕРОЯТНОСТНЫЕ МОДЕЛИ МОДЕЛИ ГЕОЛОГИЧЕСКИХ ПОЛЕЙ
Модель на основе случайной функции
Гармонический анализ
Периодограммный
анализ
Вероятностные модели геологических полей бывают нескольких видов:
Слайд 32Основой случайной функции служит предположение, что измеренные значения являются случайными
функциями координат и содержат две составляющие: математическое ожидание m(x) (закономерная
изменчивость, или тренд) и случайные колебания (x) относительно его.Если математическое ожидание – величина постоянная, то случайная функция называется стационарной, в противном случае – нестационарной.
Математическое ожидание позволяет прогнозировать значения пространственной переменной между пунктами измерений, тогда как случайные колебания служат для оценки погрешности прогнозирования.
Стационарная случайная функция может обладать еще одним свойством. Если на любом ее отрезке характеристики одинаковые, то функция эргодичная, что редко используется в геологической практике.
Измеренные значения в отдельных точках называются реализациями случайной функции.
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
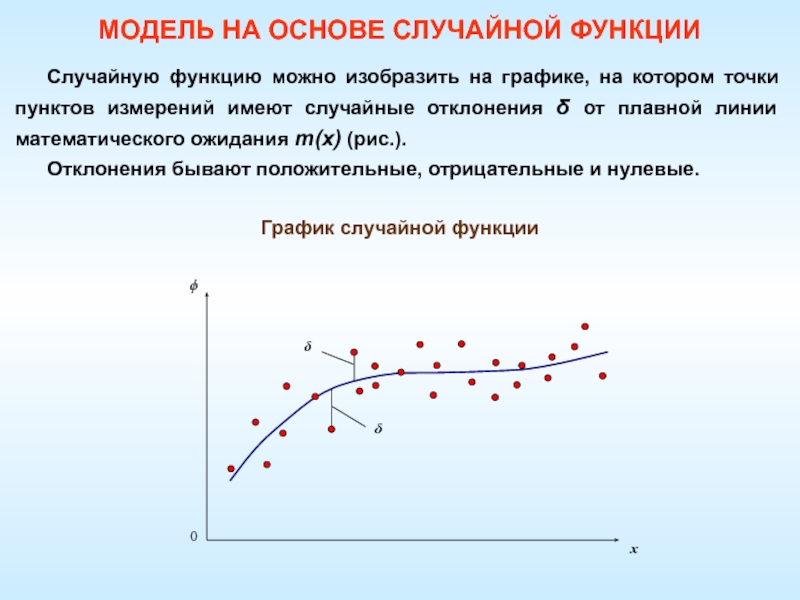
Слайд 33График случайной функции
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
Случайную функцию можно изобразить
на графике, на котором точки пунктов измерений имеют случайные отклонения
от плавной линии математического ожидания m(x) (рис.).Отклонения бывают положительные, отрицательные и нулевые.
Слайд 34Случайная функция имеет три главные характеристики: математическое ожидание, дисперсию случайных
колебаний и автокорреляционную функцию.
Математическое ожидание может рассматриваться как тренд, заданный
на основе теоретических соображений (зависимость плотности от состава руды, кривая радиоактивного распада) или эмпирическим способом, чаще всего в виде полинома. Эмпирический полином является приближенной оценкой математического ожидания.
Вычисление тренда осуществляется по методу наименьших квадратов, а наилучший порядок полинома находят в соответствии с правилом отбора информативных свойств в уравнении множественной регрессии.
Возможен еще один метод оценки математического ожидания путем сглаживания исходных данных способом скользящего окна.
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
Слайд 35Математическое ожидание стационарной случайной функции величина постоянная и равная среднеарифметическому
из всех измеренных значений.
Если из нестационарной случайной функции вычесть
математическое ожидание, то, согласно формуле:она превратится в стационарную с нулевым математическим ожиданием.
Во многих случаях математическое ожидание (закономерная изменчивость, или тренд) слабо проявлено, тогда им пренебрегают, полагая случайную функцию стационарной.
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
m(x) = f(x) + (х).
Слайд 36Дисперсия случайной функции равна дисперсии отклонений (х):
Если из дисперсии извлечь квадратный
корень, то можно получить среднеквадратичное отклонение .
Автоковариационная функция
где m
– количество слагаемых под знаком суммы; h – шаг измерений. МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
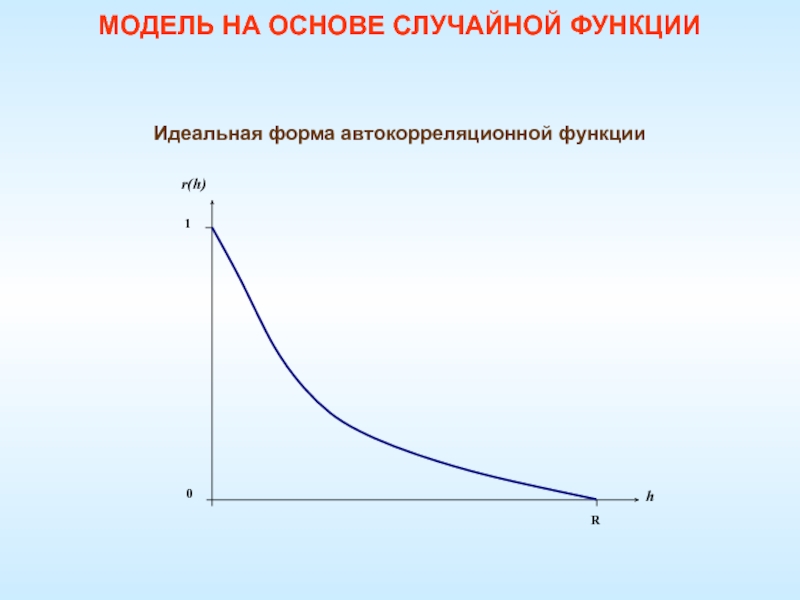
Слайд 37Она является аналогом коэффициента корреляции случайных величин, колеблется в пределах
от –1 до +1 и характеризует зависимость между отклонениями
на расстоянии h.Автокорреляционная функция зависит от шага измерений h. При нулевом шаге она равна единице, при увеличении шага убывает, приближаясь к нулю. В идеальном виде функция показана на рис.
Шаг, при котором автокорреляционная функция неотличима от нуля, называется радиусом автокорреляции R. Он является важной величиной, характеризующей радиус влияния отдельного измерения.
Особый интерес представляет автокорреляционная функция
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
Слайд 39Следует отметить, что шаг и радиус автокорреляции являются векторными величинами.
В изотропной среде радиус влияния одинаков по всем направлениям. В
анизотропной среде, а геологические объекты – большей частью анизотропные тела, радиус автокорреляции зависит от направления. Чем сильнее проявлена изменчивость в каком-либо направлении, тем меньше радиус автокорреляции. Идеальная форма автокорреляционной функции искажается по нескольким причинам. На ее форму сильнее всего влияет периодическая изменчивость, придавая кривой волнистый характер.
Если используется модель стационарной случайной функции, заметно сказывается монотонный тренд. В практических расчетах значения автокорреляционной функции находят по дискретным данным, а ее график имеет вид ломаной линии, состоящей из отдельных отрезков. В этих условиях в качестве радиуса автокорреляции принимается первое пересечение линии автокорреляции с осью абсцисс.
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
Слайд 40Изучение нестационарной случайной функции начинается с выделения математического ожидания.
С помощью заданной функции (тренда) или путем сглаживания исходных данных
с использованием скользящего окна удается выявить только оценку математического ожидания. Чаще всего задается аппроксимирующий полином, коэффициенты и порядок которого были рассмотрены ранее (Метод наименьших квадратов. Выбор порядка полинома при аппроксимации нелинейной зависимости.)После вычитания из исходных данных тренда получается остаток, т.е. случайные отклонения, у которых определяют дисперсию отклонений.
Для вычисления тренда не обязательна равномерная сеть наблюдений, но чтобы построить график исходных измерений, значения координаты х должны быть расположены в порядке возрастания.
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
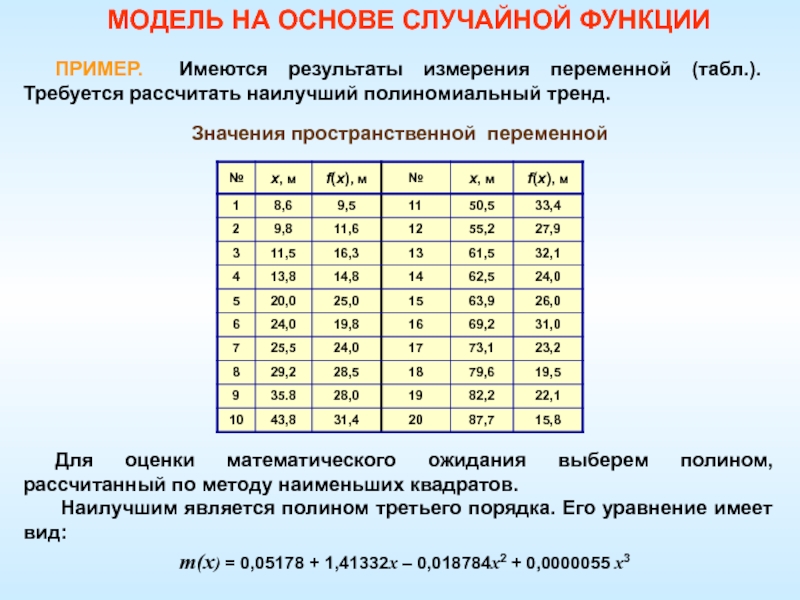
Слайд 41ПРИМЕР. Имеются результаты измерения переменной (табл.). Требуется рассчитать наилучший полиномиальный
тренд.
Значения пространственной переменной
Для оценки математического ожидания выберем полином, рассчитанный
по методу наименьших квадратов. Наилучшим является полином третьего порядка. Его уравнение имеет вид:
m(х) = 0,05178 + 1,41332х – 0,018784х2 + 0,0000055 х3
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
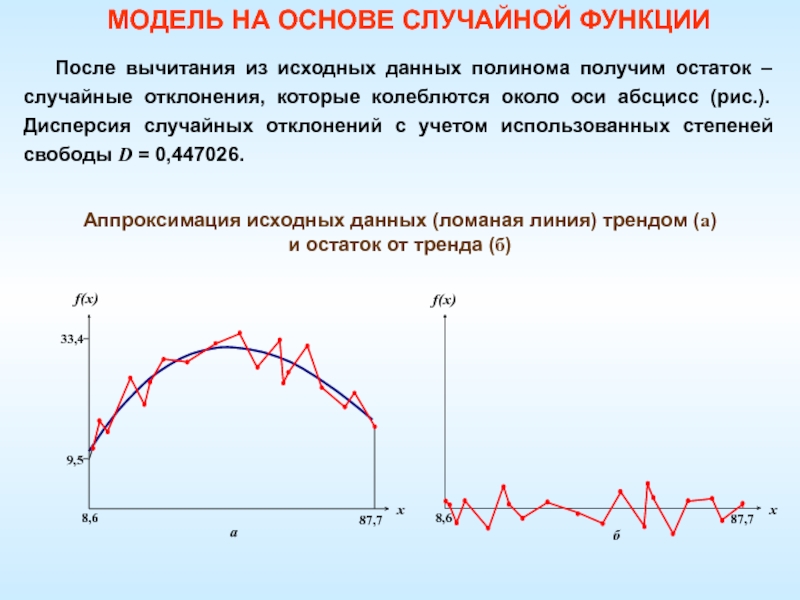
Слайд 42После вычитания из исходных данных полинома получим остаток – случайные
отклонения, которые колеблются около оси абсцисс (рис.). Дисперсия случайных отклонений
с учетом использованных степеней свободы D = 0,447026.Аппроксимация исходных данных (ломаная линия) трендом (а)
и остаток от тренда (б)
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
Слайд 43На практике часто используют двухмерный (площадной) тренд, который аппроксимируют двухмерным
полиномом невысокого порядка (не более третьего), хотя теоретически можно использовать
методику отыскания наилучшего порядка полинома.Тренды высокого порядка требуют большого объема вычислений и часто дают нереальные значения между пунктами измерений.
Еще один способ приближенной оценки математического ожидания основан на методе сглаживания исходных данных с помощью скользящего окна. Его часто называют сглаживающим фильтром и используют для выделения полезного сигнала на фоне случайных помех.
Сглаженные данные характеризуют не математическое ожидание, а тенденцию изменения пространственной переменной.
Сглаживание – простая операция, не требующая больших вычислений.
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
Слайд 44
Существует много способов сглаживания. Наиболее часто сглаживание осуществляется скользящим окном,
содержащим три соседних наблюдения. По этим трем наблюдениям находят среднеарифметическое
значение, которое сопоставляют с серединой окна. Потом окно передвигают на одно наблюдение, расчет повторяют и так поступают до конца ряда измерений.Могут быть использованы окна с различным нечетным числом измерений. Роль измерений в окне также может быть различной – центральным значениям чаще придают бóльший вес.
В случае значительного разброса исходных данных хороший результат дает медианное сглаживание, когда в окне в качестве среднего значения используют медиану.
МОДЕЛЬ НА ОСНОВЕ СЛУЧАЙНОЙ ФУНКЦИИ
Слайд 45 В составе закономерной изменчивости часто присутствует периодическая составляющая.
Из исходных данных выделить и вычесть ее можно с помощью
гармонического или периодограммного анализа.Гармонический анализ позволяет ряд исходных данных представить как сумму синусоид. В отличие от классического гармонического анализа, необходимо выделить наиболее существенные синусоиды, которые вносят основной вклад в изменчивость пространственной переменной.
Периодические явления широко распространены в природе, они находят свое выражение в ритмичном напластовании горных пород, в развитии систем упорядоченных трещин. Для выявления и характеристики периодичности, необходимо применить специальные математические приемы.
Предлагаемая методика характеризуется тем, что в ряду наблюдений последовательно находят синусоиды в порядке убывания их значимости и вычитают из исходных данных. Можно извлечь несколько (иногда одну) важнейших синусоид и этим ограничиться. Но можно извлекать синусоиды до тех пор, пока дисперсия отклонений суммы синусоид от исходных данных с учетом использованных степеней свободы не будет минимальной.
ГАРМОНИЧЕСКИЙ АНАЛИЗ
Слайд 46Каждая синусоида имеет три характеристики:
ГАРМОНИЧЕСКИЙ АНАЛИЗ
амплитуду А;
длину волны L (или обратную ей величину – частоту);
начальную фазу , поэтому каждая синусоида использует три степени свободы.
Кроме того, часто находят дисперсию синусоиды, которая пропорциональна квадрату амплитуды. Ряд значений пространственной переменной f(х) представляют в виде суммы N гармоник (синусоид) k(x):
где a0/2 – свободный член, равный среднеарифметическому значению пространственной переменной.
Слайд 47В качестве первой длины волны L чаще всего принимается длина
ряда наблюдений. Каждая гармоника k(x) выражается формулой:
или в другой форме
записи:где ak, bk – коэффициенты; k – номер гармоники (синусоиды); L/k – длина волны; Ak – амплитуда; k – начальная фаза гармоники; k = 1, 2, …, N.
Амплитуда и начальная фаза связаны с коэффициентами ak, bk соотношениями:
ГАРМОНИЧЕСКИЙ АНАЛИЗ
Слайд 48Количество гармоник N может быть большим, но на практике принимается
конечным. Количество гармоник не должно превышать n/2 (где n –
количество измерений). Наиболее правильно ограничивать их количество по минимальной дисперсии отклонений с учетом степеней свободы.Каждая синусоида использует три степени свободы, поэтому k синусоид поглощают 3k степеней свободы. Для геологических целей обычно выбирают одну или две важнейшие синусоиды, пренебрегая остальными.
За счет ограничения количества синусоид их сумма в формуле ряда значений пространственной переменной приближенно равна пространственной переменной f(х) .
ГАРМОНИЧЕСКИЙ АНАЛИЗ
Слайд 49Объединение формул ряда значений пространственной переменной f(x) и гармоники k(x)
дает ряд Фурье (гармонический ряд):
Коэффициенты ak, bk находят по формулам:
ГАРМОНИЧЕСКИЙ
АНАЛИЗСлайд 50Амплитуды гармоник (Ak) вычисляют когда определены коэффициенты ak и bk
Совокупность всех гармоник образует спектр амплитуд.
Чем больше амплитуда, тем
бόльшую роль играет соответствующая гармоника. Для количественной оценки роли гармоник используют их дисперсии Dk, совокупность которых составляет спектр дисперсий. Сумма дисперсий всех гармоник равна дисперсии пространственной переменной, что позволяет оценить роль каждой гармоники в абсолютных или относительных единицах.
Вычисление дисперсии любой гармоники лучше всего осуществлять путем сравнения остаточных дисперсий до вычитания и после вычитания гармоники из значений пространственной переменной. Уменьшение остаточной дисперсии характеризует дисперсию Dk, поглощенную данной гармоникой.
ГАРМОНИЧЕСКИЙ АНАЛИЗ
Слайд 51Периодическая изменчивость не обязательно должна быть синусоидальной, она может иметь
любую форму.
Можно выявить периодическую изменчивость любой формы путем последовательного
перебора длин волн, кратных шагу наблюдений. Такая методика, по-видимому, не описана в литературе. Предлагается назвать ее периодограммным анализом. Если имеется ряд значений пространственной переменной f(x), измеренных с шагом h, имеющих дисперсию D, то, задавая длину волны, можно выявить периодическую изменчивость (х) при данной длине волны и вычесть ее из исходных данных, что дает отклонение (х) = f(x) – (х).
Разность дисперсии исходных данных и дисперсии отклонений дает дисперсию, поглощенную периодической изменчивостью. Чем больше поглощенная дисперсия, тем сильнее проявлена периодическая изменчивость. Задавая различную длину волны, можно найти наибольшую дисперсию, что и лежит в основе периодограммного анализа.
Отыскание наилучшей длины волны начинается с наименьшей длины волны L = h. Затем длина волны последовательно увеличивается до достижения половины ряда наблюдений N = n/2.
ПЕРИОДОГРАММНЫЙ АНАЛИЗ
Слайд 53ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
В основе геостатистической группы математических моделей лежит
гипотеза о том, что случайный результат измерений обусловлен случайным расположением
сети наблюдений.При перемещении сети наблюдений результаты измерений будут другие, но сохраняется одна характеристика – средний квадрат разности между результатами измерений на расстоянии h. Это возможно при эргодичном характере пространственной переменной.
График вариограммы зависит от характера дискретности пространственной переменной.
Слайд 54ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
γ(h) + K(h) = D.
На основе гипотезы введена вариограмма γ(h)
– главная характеристика в геостатистике. Она равна полусумме среднего квадрата
разности между результатами измерений при шаге h и выражается формулой:Следует отметить, что вариограмма тесно связана со случайными функциями. Сумма вариограммы и ковариации (автокорреляционной функции) равна дисперсии исходных данных:
Слайд 55ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
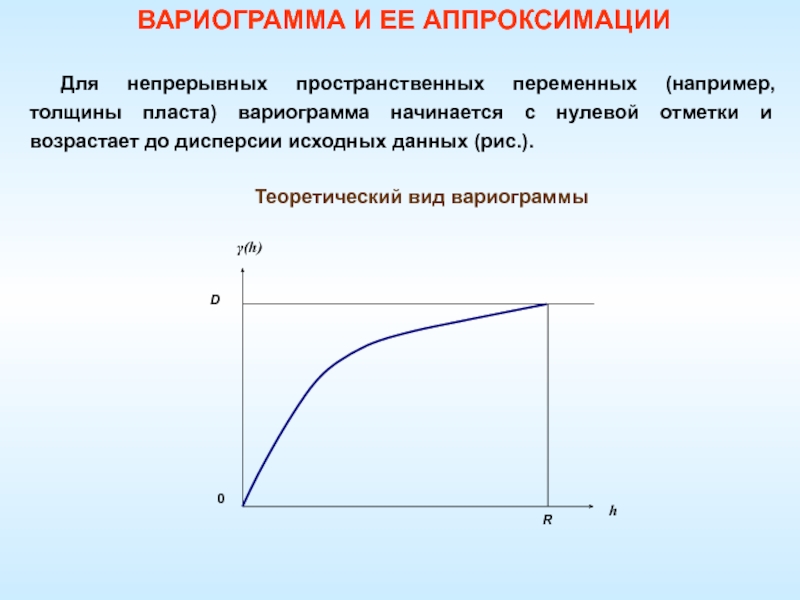
Для непрерывных пространственных переменных (например, толщины пласта)
вариограмма начинается с нулевой отметки и возрастает до дисперсии исходных
данных (рис.).Теоретический вид вариограммы
Слайд 56ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
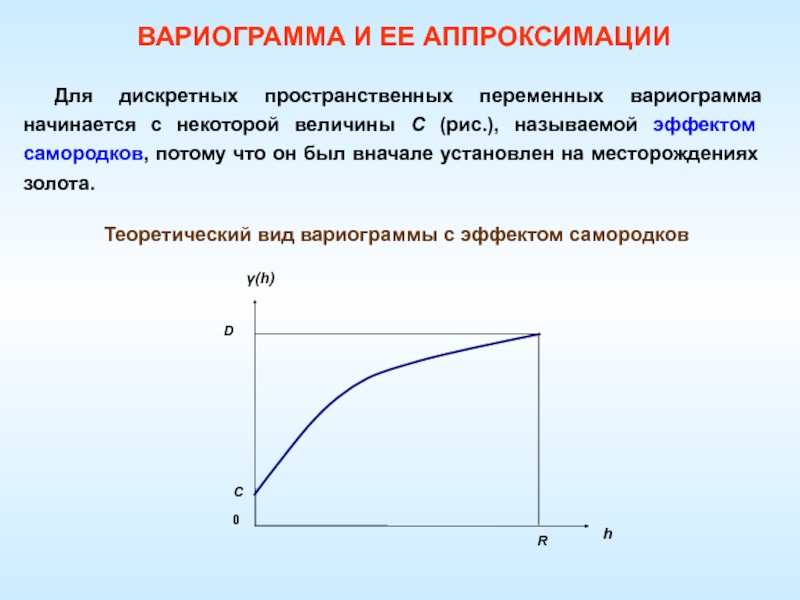
Для дискретных пространственных переменных вариограмма начинается с
некоторой величины С (рис.), называемой эффектом самородков, потому что он
был вначале установлен на месторождениях золота.Теоретический вид вариограммы с эффектом самородков
Слайд 57Вариограмма имеет радиус влияния R, который идентичен радиусу автокорреляции в
случайной функции.
За пределами радиуса влияния вариограмма постоянная и равна
дисперсии D, т.е. ее влияние отсутствует. Как упоминалось, радиус R является векторной величиной. В изотропных геологических телах по всем направлениям радиус влияния описывает окружность, за пределами которой влияние вариограммы отсутствует.
В анизотропных геологических телах значения радиуса R по разным направлениям столь различны, что напоминают восьмерку.
В пункте с координатой R вариограмма может иметь горизонтальную касательную и плавно переходить в линию дисперсии.
Эмпирическая вариограмма, получаемая на основе дискретных измерений, строится по отдельным точкам и имеет вид ломаной линии
ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
Слайд 58Эмпирическая вариограмма
ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
Для использования ее в дальнейших вычислениях,
необходимо выполнить аппроксимацию вариограммы какой-либо теоретической кривой. Вид аппроксимирующей функции
определяет вид геостатистической модели.Существует много видов аппроксимирующих функций. Наибольшее распространение получили четыре функции и, соответственно, четыре геостатистические модели.
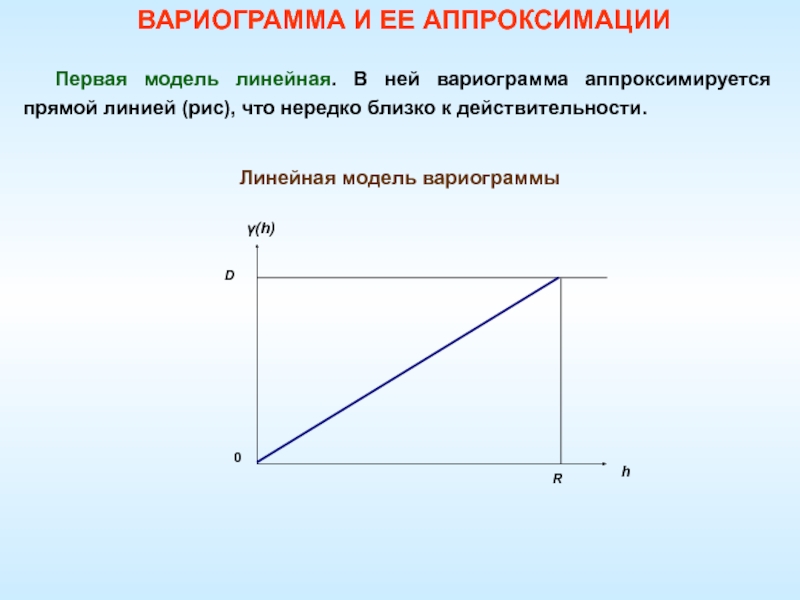
Слайд 59Линейная модель вариограммы
Первая модель линейная. В ней вариограмма аппроксимируется прямой
линией (рис), что нередко близко к действительности.
ВАРИОГРАММА И ЕЕ
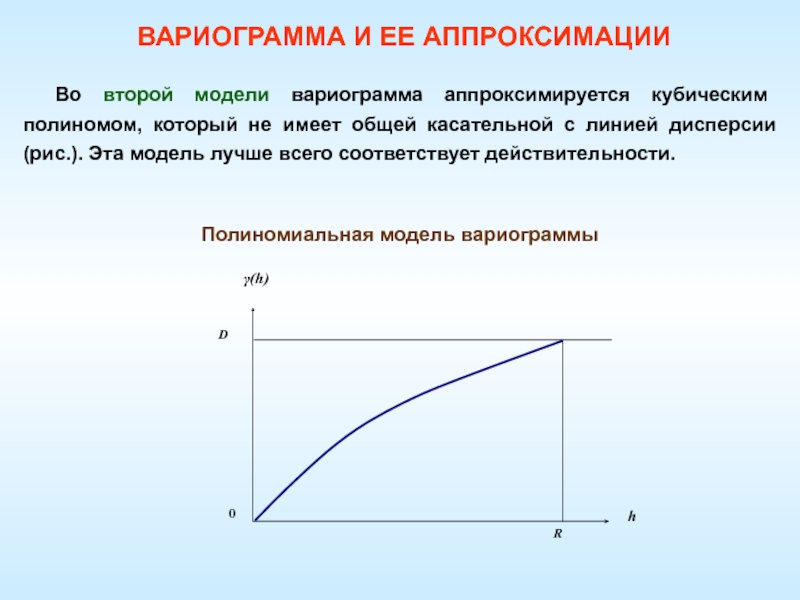
АППРОКСИМАЦИИСлайд 60Полиномиальная модель вариограммы
Во второй модели вариограмма аппроксимируется кубическим полиномом, который
не имеет общей касательной с линией дисперсии (рис.). Эта модель
лучше всего соответствует действительности.ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
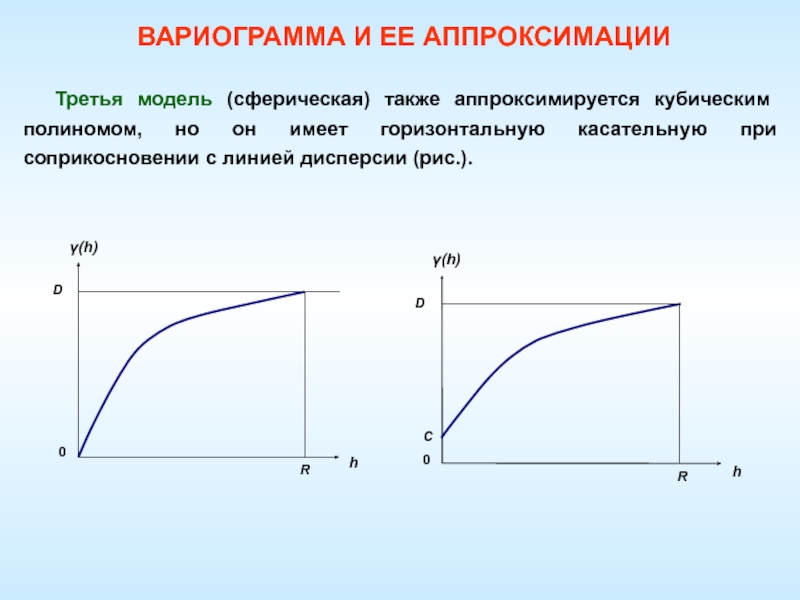
Слайд 61Третья модель (сферическая) также аппроксимируется кубическим полиномом, но он имеет
горизонтальную касательную при соприкосновении с линией дисперсии (рис.).
ВАРИОГРАММА И
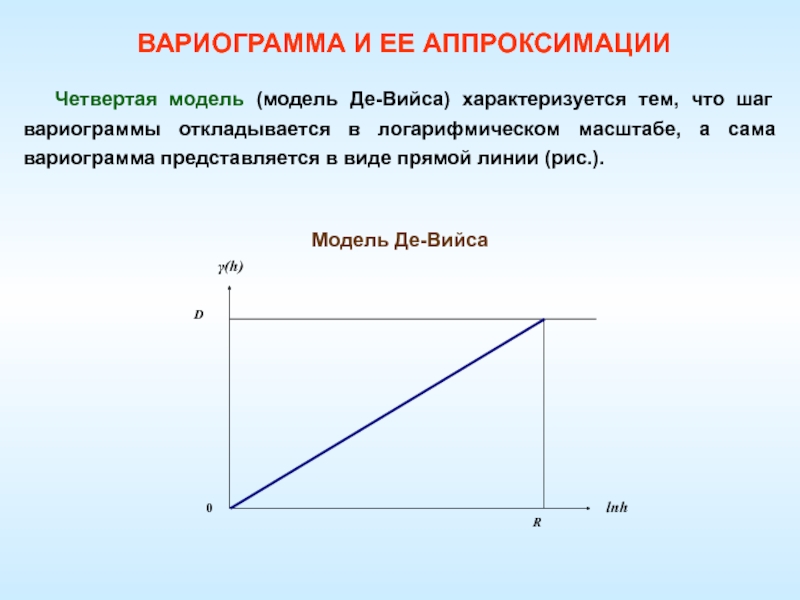
ЕЕ АППРОКСИМАЦИИСлайд 62Модель Де-Вийса
Четвертая модель (модель Де-Вийса) характеризуется тем, что шаг вариограммы
откладывается в логарифмическом масштабе, а сама вариограмма представляется в виде
прямой линии (рис.).ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
Слайд 63Выбор варианта аппроксимации носит произвольный характер. Наилучшим вариантом можно считать
тот, который дает наименьшую дисперсию отклонений эмпирических значений от теоретических.
Периодическая изменчивость свойств пространственной переменной отрицательно влияет на вид вариограммы. Вариограмма колеблется около линии дисперсии, создавая так называемый эффект включений.
При сильно выраженной периодической изменчивости радиус влияния определяется неточно.
ВАРИОГРАММА И ЕЕ АППРОКСИМАЦИИ
Слайд 64Многие характеристики пространственной переменной зависят от геометрической базы измерений, т.е.
от формы, размеров, а в анизотропных телах и от ориентировки
области измерений. К таким характеристикам, в первую очередь, относятся дисперсия и вариограмма.Если область, в которой производится измерение, настолько мала, что ее размерами можно пренебречь, то измерение рассматривается как точечное. Характеристики, полученные из таких измерений, рассматриваются как измерения на точечной геометрической базе.
ВЛИЯНИЕ НА ВАРИОГРАММУ ГЕОМЕТРИЧЕСКОЙ БАЗЫ ИЗМЕРЕНИЙ
Слайд 65Пусть в геологическом объекте имеется множество точек, в каждой из
которых пространственная переменная имеет значение f(x). Если геологическое объект разделить
на области объемом v и в каждом из них найти среднее из N точечных значений, то получим новую пространственную переменную fv(x):ВЛИЯНИЕ НА ВАРИОГРАММУ ГЕОМЕТРИЧЕСКОЙ БАЗЫ ИЗМЕРЕНИЙ
где p(m) – весовая функция, зависящая от взаимного расположения точек в объеме v.
Слайд 66При увеличении размеров геометрической базы происходит усреднение значений пространственной переменной,
соответственно, будут меняться некоторые статистические характеристики.
При переходе к бесконечному
множеству точек в объеме v пространственная переменная преобразуется в интегральную форму:ВЛИЯНИЕ НА ВАРИОГРАММУ ГЕОМЕТРИЧЕСКОЙ БАЗЫ ИЗМЕРЕНИЙ
Нахождение средних значений fv(x) по точечным значениям f(x) называется регуляризацией (сглаживанием) пространственной переменной в объеме v.
Меняя объем v, будем получать различные регуляризованные пространственные переменные, соответственно, будут меняться и их характеристики.
Слайд 67Изменение дисперсии по мере увеличения объема v описывается формулой:
Вычитаемое в
данной формуле представляет собою среднее значение вариограммы, получаемое при всех
возможных положениях точек i и j в объеме v.При переходе к бесконечному множеству точек формула приобретает интегральный вид:
где D – дисперсия пространственной переменной на точечной базе; N – число точек в объеме v.
По мере увеличения объема v дисперсия пространственной переменной уменьшается.
ВЛИЯНИЕ НА ВАРИОГРАММУ ГЕОМЕТРИЧЕСКОЙ БАЗЫ ИЗМЕРЕНИЙ
Слайд 68Подобные формулы существуют и для вариограммы:
или в интегральной форме
Первое слагаемое
в этих формулах характеризует среднюю ковариограмму, которая получается как средняя
из вариограмм между всеми точками в объеме v, а вычитаемое – в таком же объеме, смещенном на расстояние h.ВЛИЯНИЕ НА ВАРИОГРАММУ ГЕОМЕТРИЧЕСКОЙ БАЗЫ ИЗМЕРЕНИЙ
Слайд 69где k(х) = 1, когда точка х находится внутри геологического объекта, k(х) = 0,
когда точка х находится за его пределами.
Представленные формулы выведены
в предположении, что объем v мал по сравнению с объемом изучаемого геологического объекта, иначе сказывается граничный эффект, который можно учесть введением специальной весовой функции – геометрической ковариограммы p(h):ВЛИЯНИЕ НА ВАРИОГРАММУ ГЕОМЕТРИЧЕСКОЙ БАЗЫ ИЗМЕРЕНИЙ
Слайд 70Геометрический смысл ковариограммы заключается в степени перекрытия двух объемов, смещенных
относительно друг друга на расстояние h. С учетом функции p(h)
получаем формулы :Если вариограмма аппроксимирована каким-либо алгебраическим выражением, т.е. задан вид математической модели, то интегралы во многих случаях могут быть вычислены и заменены соответствующими алгебраическими выражениями.
ВЛИЯНИЕ НА ВАРИОГРАММУ ГЕОМЕТРИЧЕСКОЙ БАЗЫ ИЗМЕРЕНИЙ
Слайд 71На основе геостатистических моделей создан новый метод интерполяции результатов между
пунктами измерений, который получил название кригинг (крайгинг) в честь автора
метода Д.П.Крига.Кригинг дает минимальную сумму квадратов отклонений прогнозных значений от фактических значений пространственной переменной.
Существует несколько видов кригинга.
Вначале рассмотрим простейший – точечный кригинг.
ПОНЯТИЕ О КРИГИНГЕ
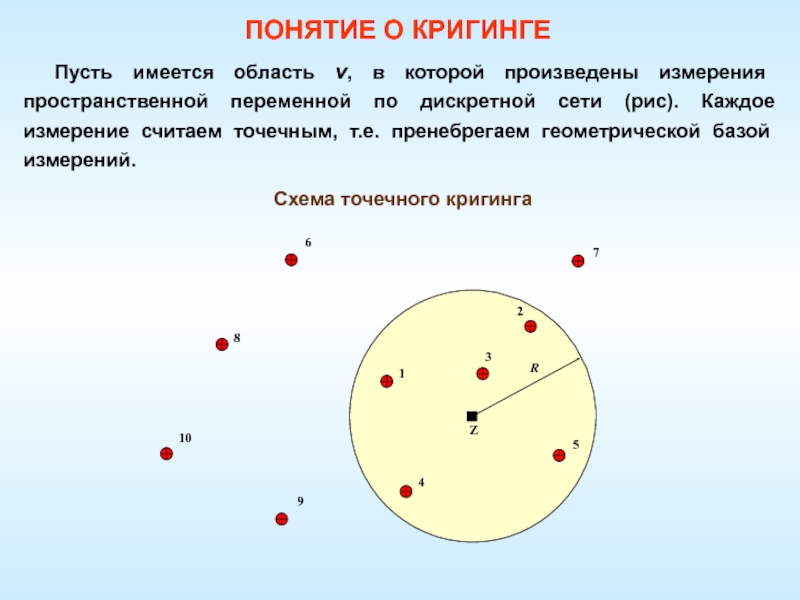
Слайд 72Схема точечного кригинга
ПОНЯТИЕ О КРИГИНГЕ
Пусть имеется область v, в которой
произведены измерения пространственной переменной по дискретной сети (рис). Каждое измерение
считаем точечным, т.е. пренебрегаем геометрической базой измерений.Слайд 73ПОНЯТИЕ О КРИГИНГЕ
геологический объект изотропный, тогда вокруг точки Z можно
провести окружность с радиусом влияния R.
все измерения внутри окружности
влияют на значение пространственной переменной в точке Z. за пределами окружности результаты измерений в прогнозировании не участвуют.
Необходимо рассчитать прогнозное значение пространственной переменной в точке Z.
Предположим, что:
Слайд 74Прогнозное значение находится в результате выполнения ряда последовательных операций:
1.
Рассчитывается эмпирическая вариограмма.
2. Осуществляется аппроксимация эмпирической вариограммы теоретической вариограммой,
т.е. выбирается геостатистическая модель.3. В области с радиусом R рассчитываются все расстояния между пунктами измерений, а также между пунктами измерений и пунктом прогноза.
4. Составляется симметричная система уравнений кригинга следующего вида:
Здесь 12 – значение теоретической вариограммы между пунктами 1 и 2 (учитывается расстояние между этими пунктами); m – количество пунктов, участвующих в расчете (в данном случае m = 5).
ПОНЯТИЕ О КРИГИНГЕ
Слайд 755. Решение системы дает весовые коэффициенты p1, p2, p3, …,
pm.
6. Сумма весовых коэффициентов должна быть равна единице, для
чего все коэффициенты делятся на их сумму.7. С помощью весовых коэффициентов вычисляется прогнозное значение свойства в пункте Z:
где zi – значения свойства в пунктах c 1-го по m-й.
ПОНЯТИЕ О КРИГИНГЕ
Слайд 76При необходимости вычисления прогнозного значения в следующем пункте, то операции
№3-6 выполняются снова.
Кригинг нельзя применять, если в пределах радиуса
влияния не окажется ни одного пункта измерения. В этом случае обращаются к другим методам интерполяции данных, чаще всего используется метод обратных расстояний.В случае когда при составлении системы уравнений в матрице коэффициентов оказывается много нулей (расстояния между точками больше радиуса автокорреляции, система уравнений является несовместимой, т.е. не имеет решения (или имеет много решений). Весовые коэффициенты лучше всего находить путем деления значений D – γ1z, D – γ2z, D – γ3z, , D – γmz на дисперсию D и потом приводить сумму коэффициентов к единице.
ПОНЯТИЕ О КРИГИНГЕ
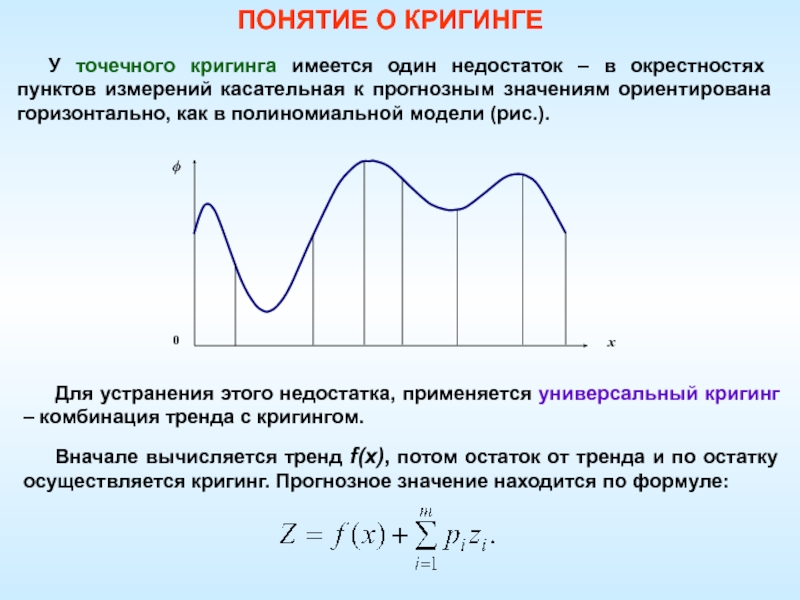
Слайд 77У точечного кригинга имеется один недостаток – в окрестностях пунктов
измерений касательная к прогнозным значениям ориентирована горизонтально, как в полиномиальной
модели (рис.).ПОНЯТИЕ О КРИГИНГЕ
Для устранения этого недостатка, применяется универсальный кригинг – комбинация тренда с кригингом.
Вначале вычисляется тренд f(x), потом остаток от тренда и по остатку осуществляется кригинг. Прогнозное значение находится по формуле:
Слайд 78ПОНЯТИЕ О КРИГИНГЕ
В качестве тренда используется аппроксимирующий полином не выше
третьего порядка.
Использование тренда частично снимает явление анизотропии, что позволяет
применять изотропную схему кригинга.Точечный кригинг можно распространить на объем v. Во всех точках объема с помощью кригинга рассчитывают прогнозное значение свойства, а потом находят среднее из всех значений. Если пункты измерений не точечные, а имеют какой-то объем, то при прогнозировании учитывают все точки в этом объеме. Практически все задачи с объемными геометрическими базами решаются путем вычисления определенных интегралов по этим объемам численными методами.