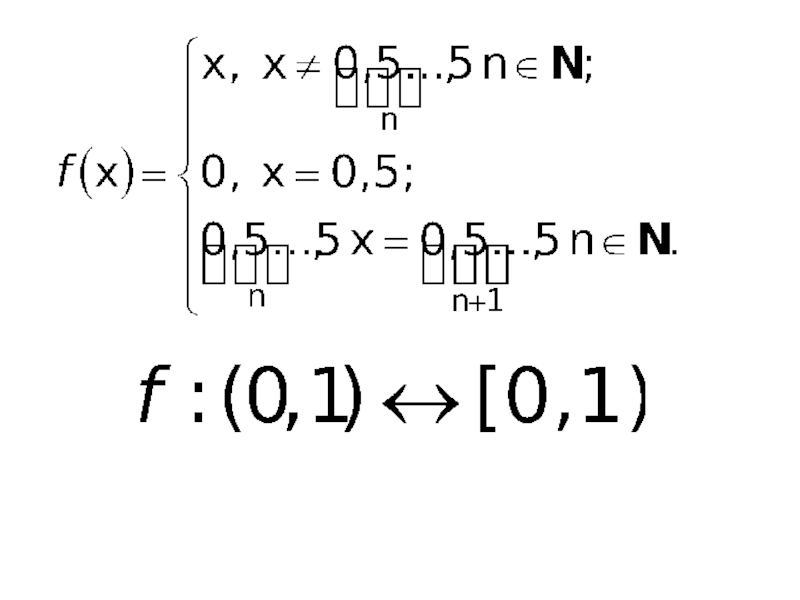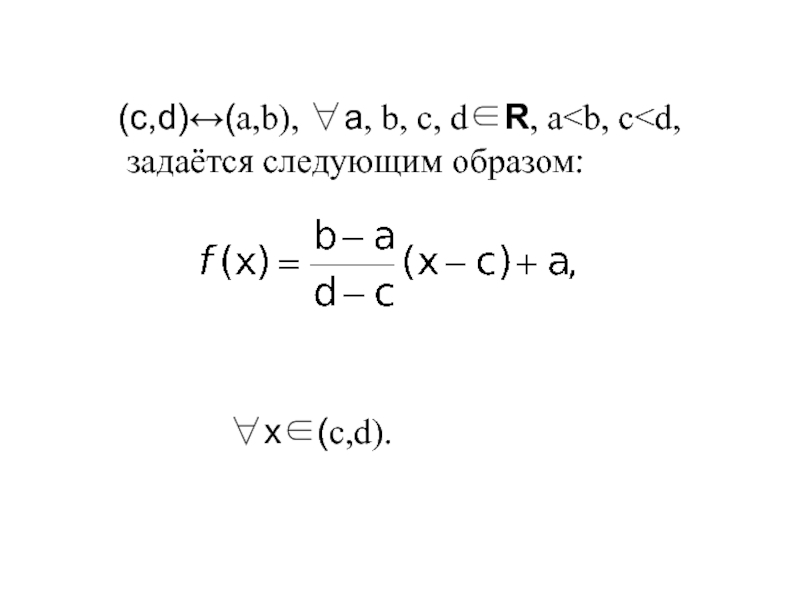Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
л5.ppt
Содержание
- 1. л5.ppt
- 2. Счётное множествоПусть N/ ⊂ Nn1; в N/ \{n1} n2; в N/ \{n1, n2} ∅, если n=1, {1, 2,…, n–1}, если 1
- 3. Счётным является множество всех целых чисел Z f: Z→N.
- 4. Множество N2 счетное N2={(m, n) | m, n∈N} N2 = {(1, 1)}N3={(1, 2), (2, 1)}N4={(1, 3), (2, 2), (3, 1)}Ni = {(1, i–1), (2, i–2), (3, i–3),…, (i–1, 1)
- 5. Слайд 5
- 6. 0,α1α2α3… 0,β1β2β3… β1≠α11, β2≠α22, β3≠α33 Теорема (Г. Кантор). Множество всех действительных чисел интервала (0,1) несчётно.
- 7. Слайд 7
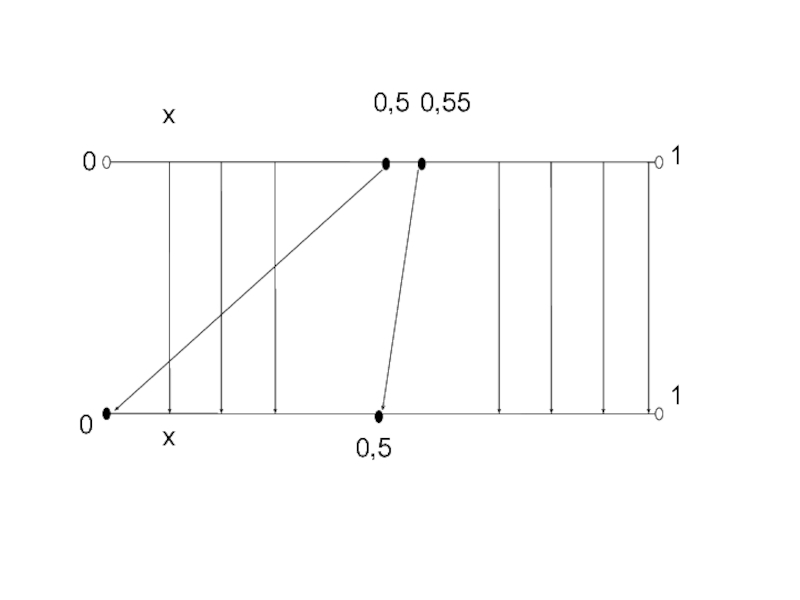
- 8. Слайд 8
- 9. Слайд 9
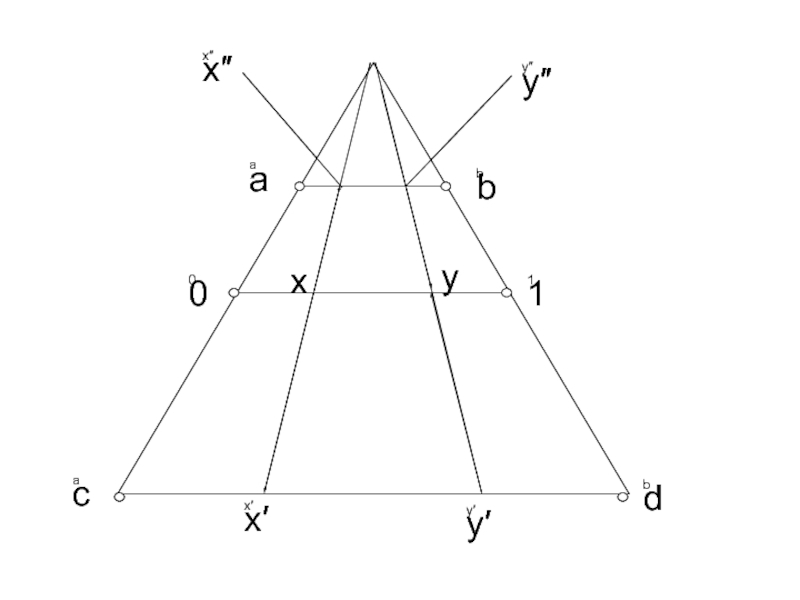
- 10. (c,d)↔(a,b), ∀a, b, c, d∈R, a
- 11. Скачать презентанцию
Счётное множествоПусть N/ ⊂ Nn1; в N/ \{n1} n2; в N/ \{n1, n2} ∅, если n=1, {1, 2,…, n–1}, если 1