Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Lecture 09 The Distribution of Molecules over Velocities Maxwell
Содержание
- 1. Lecture 09 The Distribution of Molecules over Velocities Maxwell
- 2. BAR CHARTSmooth CHART – distribution functionx x+aΔPx SOME MATHEMATICS: the probability distribution
- 3. Normal distributionThe normal (or Gauss) distribution –
- 4. Gauss DistributionThe normal distribution is very often
- 5. Statistical Entropy in Molecular Physics: the logarithm
- 6. Слайд 6
- 7. Not a strict proof, but plausible considerations.
- 8. Statistical Entropy and the Entropy of Ideal
- 9. The Distributions of Molecules over Velocities and
- 10. If gas is in thermodynamic equilibrium state
- 11. Each velocity vector can be presented as
- 12. The probability that the end of the
- 13. Noe some mathematics: We will calculate the derivative by dVx asDistribution of molecules over velocities
- 14. The only function which satisfies the equation:
- 15. From normalization condition : we obtain: The Poisson integral:Distribution of molecules over velocities
- 16. THE PROPERTIES OF AVERAGES. Average of the
- 17. Probability Distribution and Average ValuesExamples: in case
- 18. Different Kinds of AveragesYXZV = = 3R/4
- 19. The average of the squared velocity equals
- 20. The basic assumption of thermodynamics (every degree
- 21. The distribution over absolute values of velocities:,Distribution of molecules over velocities
- 22. Function defines the probability that velocity is within
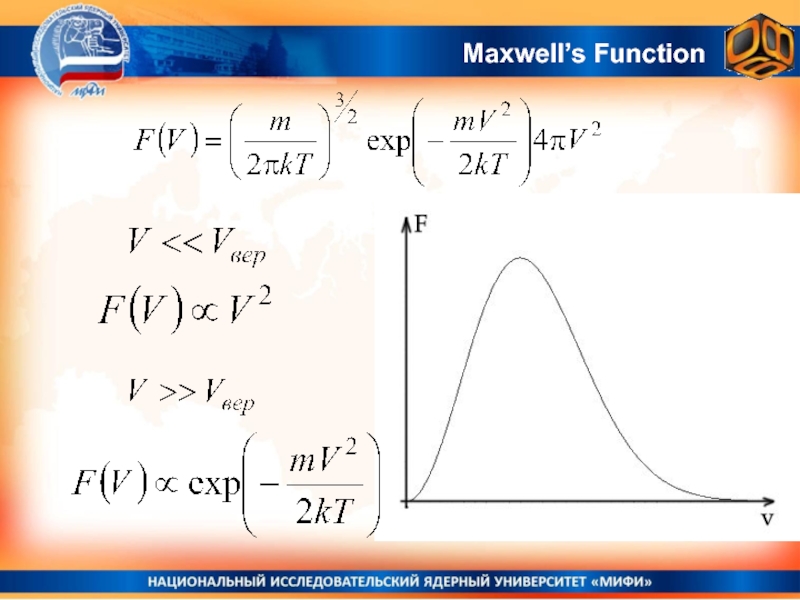
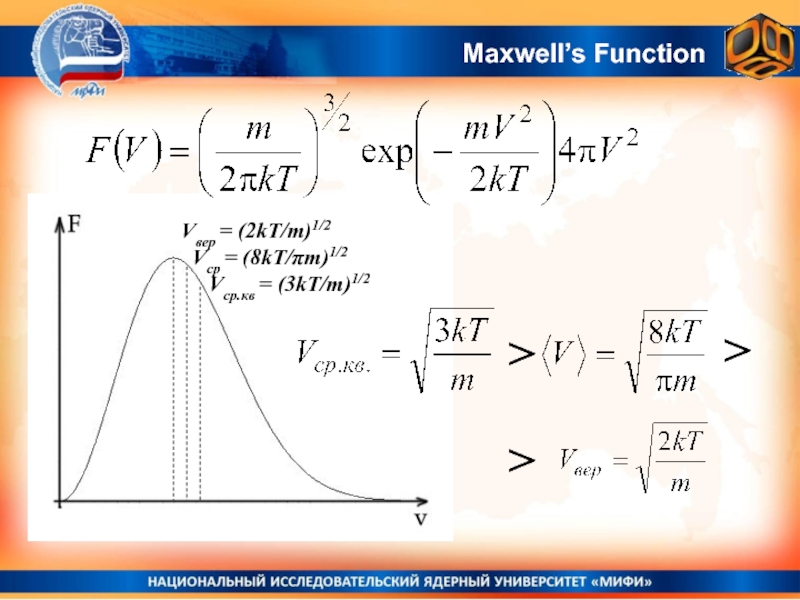
- 23. Maxwell’s Function
- 24. Area under the curve is always equal to 1Maxwell’s Function
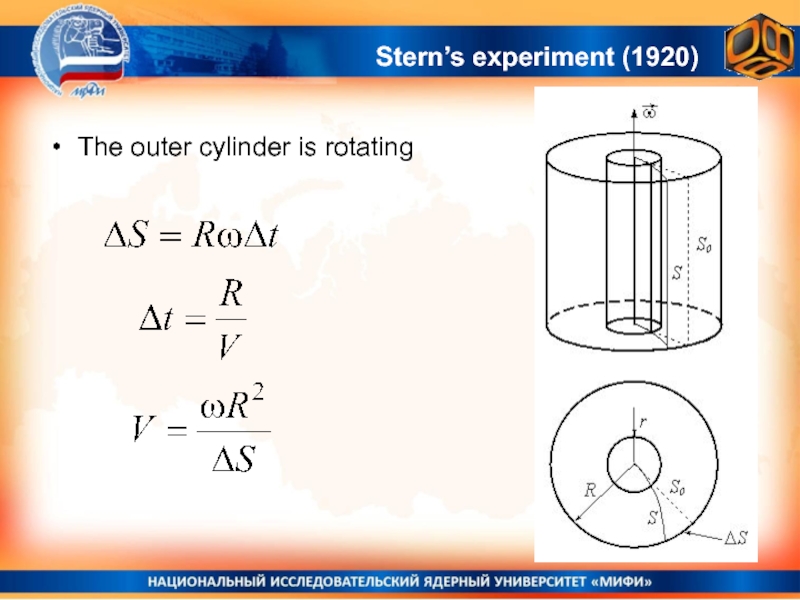
- 25. Stern’s experiment (1920)The outer cylinder is rotating
- 26. Lammert’s Experiment (1929)Two rotating discs with radial
- 27. Most probable velocity.Most probable velocity corresponds to
- 28. Average velocity.Average velocity by deffinitionFor Maxwell’s function:
- 29. Average squared velocity by definitionAverage squared velocity.
- 30. Most probable:Averge:Average squared:Three kinds of average velocities
- 31. Maxwell’s FunctionVвер = (2kT/m)1/2 Vср = (8kT/πm)1/2 Vср.кв = (3kT/m)1/2 > >>
- 32. Example: Example: The mixture of oxygen and
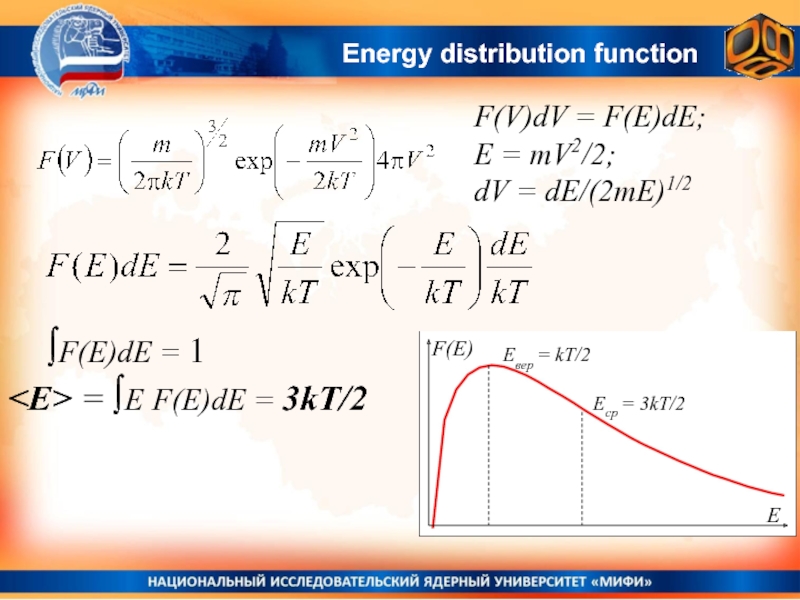
- 33. Energy distribution functionF(V)dV = F(E)dE; E =
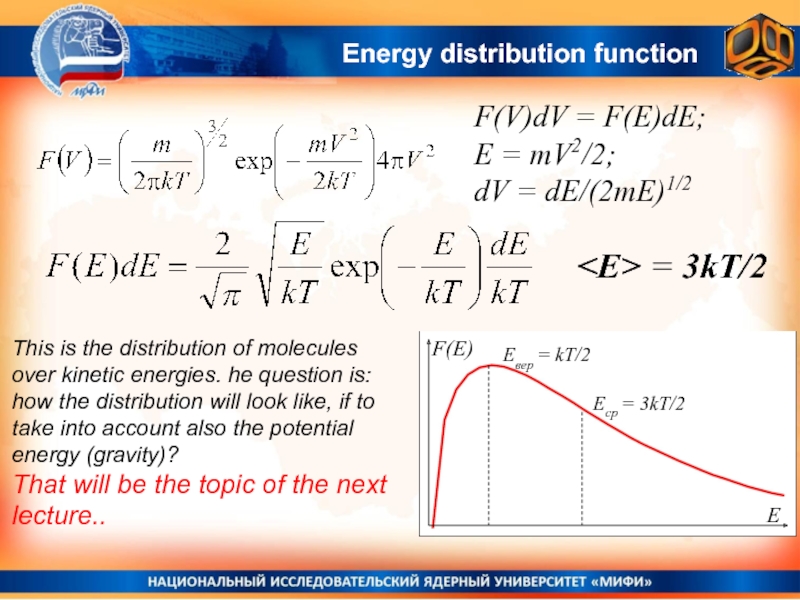
- 34. Energy distribution functionF(V)dV = F(E)dE; E =
- 35. Thank You for Attention!
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Lecture 09
The Distribution of Molecules
over Velocities
Maxwell Distribution
MEPhI General Physics
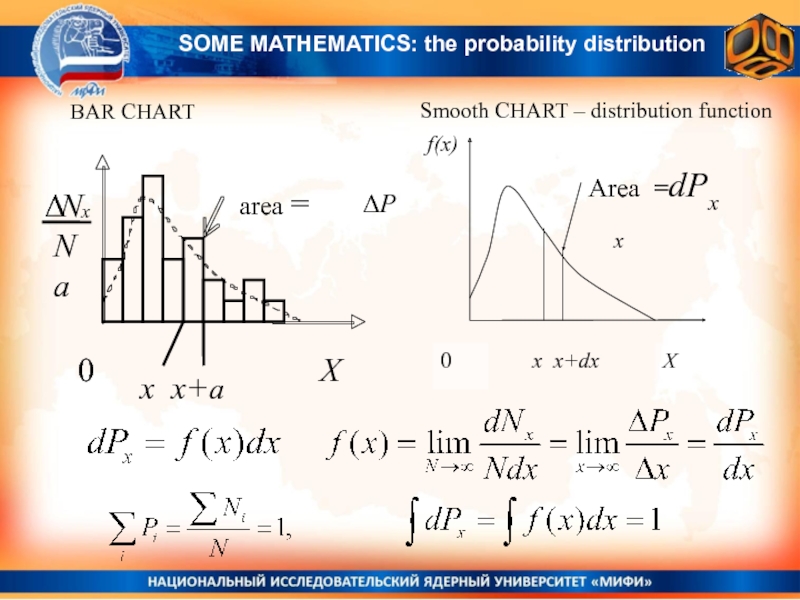
Слайд 2BAR CHART
Smooth CHART – distribution function
x x+a
ΔP
x
SOME MATHEMATICS: the
probability distribution
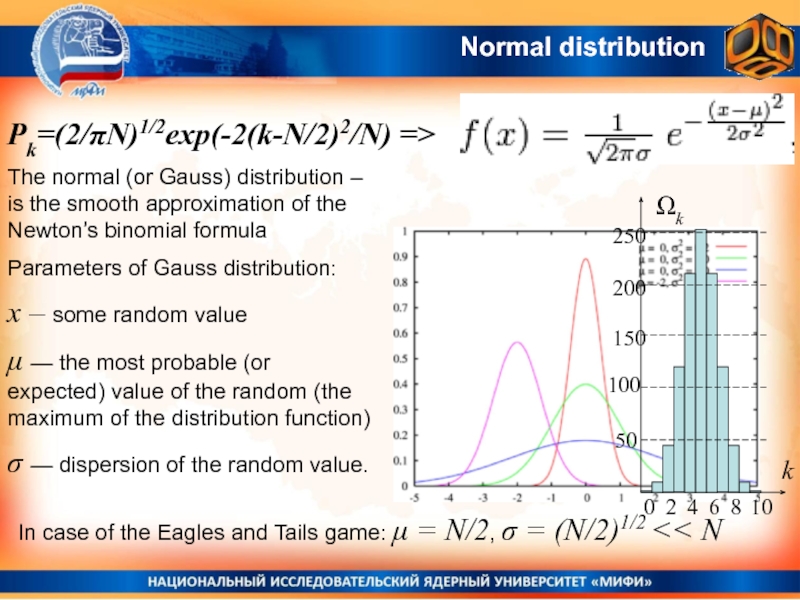
Слайд 3Normal distribution
The normal (or Gauss) distribution – is the smooth
approximation of the Newton’s binomial formula
Parameters of Gauss distribution:
x –
some random valueμ — the most probable (or expected) value of the random (the maximum of the distribution function)
σ — dispersion of the random value.
In case of the Eagles and Tails game: μ = N/2, σ = (N/2)1/2 << N
Pk=(2/πN)1/2exp(-2(k-N/2)2/N) =>
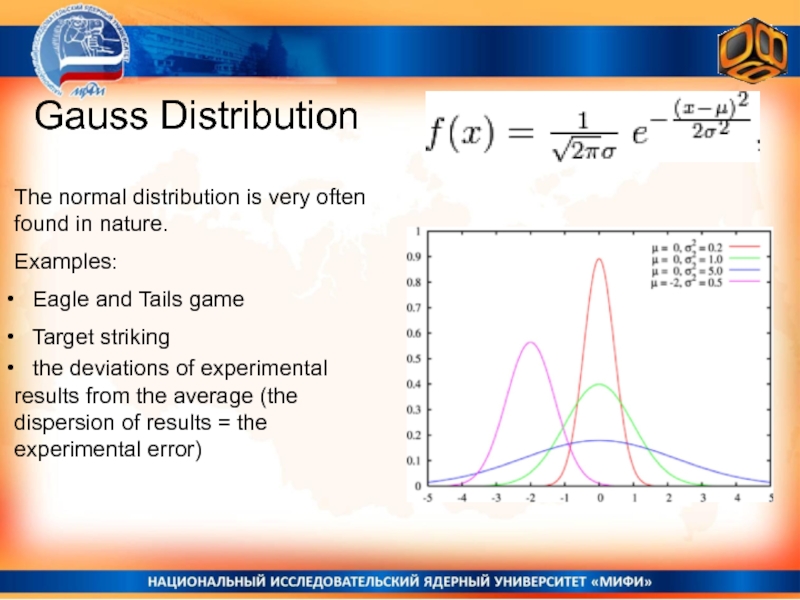
Слайд 4Gauss Distribution
The normal distribution is very often found in nature.
Examples:
Eagle and Tails game
Target striking
the deviations of experimental results from the average (the dispersion of results = the experimental error)Слайд 5 Statistical Entropy in Molecular Physics: the logarithm of the number
of possible micro-realizations of a state with certain macro-parameters, multiplied
by the Boltzmann constant.In the state of thermodynamic equilibrium, the entropy of a closed system has the maximum possible value (for a given energy).
If the system (with the help of external influence)) is derived from the equilibrium state - its entropy can become smaller. BUT…
If a nonequilibrium system is left to itself - it relaxes into an equilibrium state and its entropy increases
The entropy of an isolated system for any processes does not decrease, i.e. ΔS > 0 , as the spontaneous transitions from more probable (less ordered) to less probable (more ordered) states in molecular systems have negligibly low probability
J/K
Statistical Entropy in Physics.
5. The entropy is the measure of disorder in molecular systems.
Слайд 6
Entropy is the
additive quantity.
J/К
Statistical Entropy in Physics.
For the state of the
molecular system with certain macroscopic parameters we may introduce the definition of Statistical Entropy as the logarithm of the number of possible micro-realizations (the statistical weight of a state Ώ) - of a this state, multiplied by the Boltzmann constant.Слайд 7Not a strict proof, but plausible considerations.
Statistical Entropy and
the Entropy of Ideal Gas
the number of variants
of realization of a state (the statistical weight of a state) shall be higher, if the so called phase volume, available for each molecule (atom), is higher: Phase volume Ω1 ~Vp3~VE3/2 ~VT3/2 As molecules are completely identical, their permutations do not change neither the macrostate, nor the microstates of the system. Thus we have to reduce the statistical weight of the state by the factor ~ N! (the number of permulations for N molecules)
the phase volume for N molecules shall be raised to the power N:
Ω ~ VNT3N/2.
For multy-atomic molecules, taking into account the possibilities of rotational and oscillational motion, we shall substitute 3 by i : Ω ~ VNT iN/2
Ω~ VNTiN/2 /N!; S=k ln Ω =kNln(VTi/2/NC)=
= v(Rln(V/v) + cVlnT +s0)
Слайд 8
Statistical Entropy and the Entropy of Ideal Gas
Ω~ VNTiN/2 /N!;
S=k ln Ω =kNln(VTi/2/NC)=
= v(Rln(V/v) + cVlnT +s0)
The statistical entropy proves
to be the same physical quantity, as was earlier defined in thermodynamics without even referring to the molecular structure of matter and heat! Слайд 9
The Distributions of Molecules
over Velocities and Energies
Maxwell and Boltzmann
Distributions
That will be the Focus of the next lecture!
MEPhI General
PhysicsСлайд 10If gas is in thermodynamic equilibrium state –the macroscopic parameters
(temperature, pressure) are kept stable and the distribution of molecules
over velocities and energies remains also stable in time and space.This distribution was first derived in 1859 by J.C.Maxwell.
Distribution of molecules over velocities
James Clerk Maxwell
1831-1879
Слайд 11Each velocity vector can be presented as a point in
the velocity space,
As all the directions are equal –
the distribution function can not depend on the direction, but only on the modulus of velocity f(V)Distribution of molecules over velocities
Слайд 12The probability that the end of the 3-dimensional velocity vector
V, will fir into the small cube
nearby the velocity V can be calculated by multiplying probabilities:The probability to have the x-component of the velocity within the range between Vx and Vx+dVx
From the other hand, as all the directions are equal, this probability may depend only on the modulus of velocity
dP(V)
Distribution of molecules over velocities
Слайд 13 Noe some mathematics:
We will calculate the derivative by dVx
as
Distribution of
molecules over velocities
Слайд 14 The only function which satisfies the equation:
as well as
the initial condition
here α must be negative! α
molecules over velocitiesСлайд 15From normalization condition : we obtain:
The Poisson integral:
Distribution
of molecules over velocities
Слайд 16THE PROPERTIES OF AVERAGES.
Average of the sum of two
values equals to the sum of their averages
= Average of the product of two values equals to the product of their averages ONLY in case if those two values DO NOT depend on each other
Probability Distribution and Average Values
Knowing the distribution of a random value x we may calculate its average value Moreover, we may calculate the average for any function ψ(x):
Слайд 17Probability Distribution and Average Values
Examples: in case of even distribution
of molecules over certain spherical volume V (balloon with radius
R):Y
X
Z
V
= 0
Calculation – on the blackboard…
Слайд 18Different Kinds of Averages
Y
X
Z
V
= = 3R/4
- average
()1/2 = 0,61/2R > - squared average
=
0; Median average rmed ; the quantity of molecules with r
rmed = R/21/3 = 0,7937R > (
This all is about even distribution of molecules over space in spherical balloon.
What about the distribution of molecules over velocities and energies?
It can be spherically symmetric, but it can not be even as formally there is no upper limit of velocity…
Слайд 19 The average of the squared velocity equals to:
This integral once
again can be reduced to the Poisson integral:
Distribution of molecules
over velocitiesСлайд 20The basic assumption of thermodynamics (every degree of freedom accumulates
the same energy):
Distribution of molecules over velocities
Слайд 21 The distribution over absolute values of velocities:
,
Distribution of molecules over
velocities
Слайд 22 Function
defines the probability that velocity is within the “cubic” range:
Probability to find the absolute value of the velocity between
V and V+dV- Maxwell’s function
Distribution of molecules over velocities
Слайд 26Lammert’s Experiment (1929)
Two rotating discs with radial slots. One is
rotating ahead of the other. The angle distance is
Слайд 27Most probable velocity.
Most probable velocity corresponds to the maximum of
the Maxwell’s function)
Most probable velocity
The value of the Maxwell’s
function maximum: Vвер
Слайд 32Example:
Example: The mixture of oxygen and nitrogen (air) has
the temperature T = 300 K. What are the average
velocities of two types of molecules:Слайд 33Energy distribution function
F(V)dV = F(E)dE;
E = mV2/2;
dV =
dE/(2mE)1/2
∫F(E)dE = 1
= ∫E F(E)dE = 3kT/2
Слайд 34Energy distribution function
F(V)dV = F(E)dE;
E = mV2/2;
dV =
dE/(2mE)1/2
= 3kT/2
This is the distribution of molecules over
kinetic energies. he question is: how the distribution will look like, if to take into account also the potential energy (gravity)?That will be the topic of the next lecture..