Лекция 8а.ppt

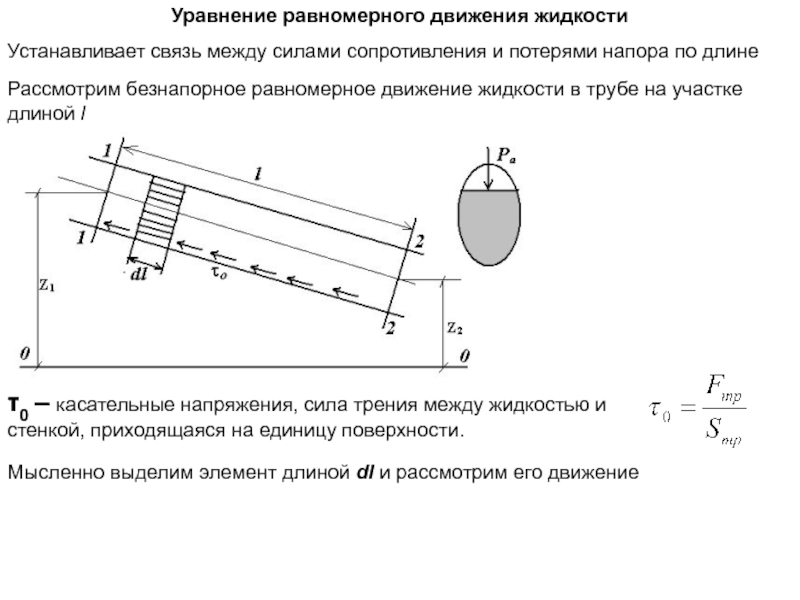
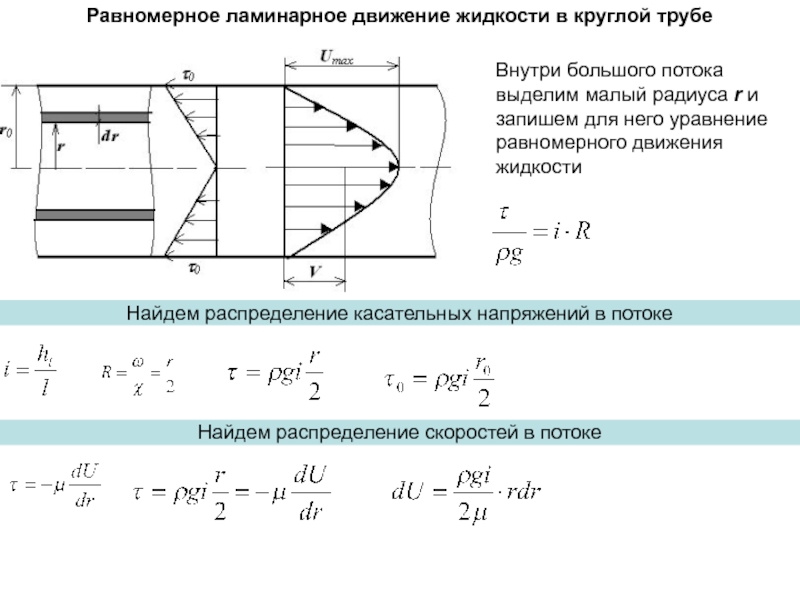
напора по длине
Рассмотрим безнапорное равномерное движение жидкости в трубе на

τ0 – касательные напряжения, сила трения между жидкостью и стенкой, приходящаяся на единицу поверхности.

Мысленно выделим элемент длиной dl и рассмотрим его движение

2 – 2
Работа сил трения при перемещении отсека из

Данная работа совершается за счет изменения потенциальной энергии положения

Данное выражение справедливо и для напорного движения, а также для любого равномерного малого потока, выделенного внутри большого.

малый радиуса r и запишем для него уравнение равномерного движения

Найдем распределение касательных напряжений в потоке

Найдем распределение скоростей в потоке

скорость потока.
На расстоянии r от центра выделим кольцевой элемент толщиной

Луи Мари Пуазейля
Данная формула показывает всю сложность борьбы с сердечно-сосудистыми

Уменьшение диаметра на 10% приводит к возрастанию перепада давления в 1,52 раза

Получим из закона Пуазейля коэффициент гидравлического трения

Расчетные формулы
Равномерное ламинарное движение жидкости в зазоре между двумя стенками

Перепада давления нет, движение фрикционное.

из которых движется с постоянной скоростью при перепаде давления
Равномерное ламинарное

При эксцентрично расположенной щели и эксцентриситете =а расход увеличивается в 2.5 раза