Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекции 13-14
Содержание
- 1. Лекции 13-14
- 2. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 3. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 4. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 5. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 6. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 7. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 8. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 9. КГТУ (КАИ), кафедра АСОИУПример представления дерева в виде сетей и списковой структуры
- 10. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 11. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 12. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 13. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 14. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 15. КГТУ (КАИ), кафедра АСОИУ // Прототипы функцийvoid
- 16. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 17. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 18. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 19. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.Р.КГТУ (КАИ), кафедра
- 20. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.Р.КГТУ (КАИ), кафедра
- 21. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 22. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.Р.КГТУ (КАИ), кафедра
- 23. КГТУ (КАИ), кафедра АСОИУ Бикмурзина А.РКГТУ (КАИ), кафедра
- 24. КГТУ (КАИ), кафедра АСОИУ Три способа обхода
- 25. КГТУ (КАИ), кафедра АСОИУДерево выражения и способы
- 26. КГТУ (КАИ), кафедра АСОИУПример дерева выражения
- 27. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 28. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 29. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 30. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 31. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 32. КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра
- 33. Скачать презентанцию
КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра АСОИУДеревьяДерево – это связный граф без циклов.Связным называют граф, в котором для любых двух вершин существует связывающий их путь. Дерево из n вершин имеет
Слайды и текст этой презентации
Слайд 2КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Деревья
Дерево – это
связный граф без циклов.
Связным называют граф, в котором для любых
двух вершин существует связывающий их путь. Дерево из n вершин имеет n-1 ребер. Дерево с одной выделенной вершиной называют корневым, а выделенную вершину – корнем дерева.
Корневое дерево обычно рассматривают как ориентированное от корня (реже к корню), но изображают без стрелок.
Слайд 3КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
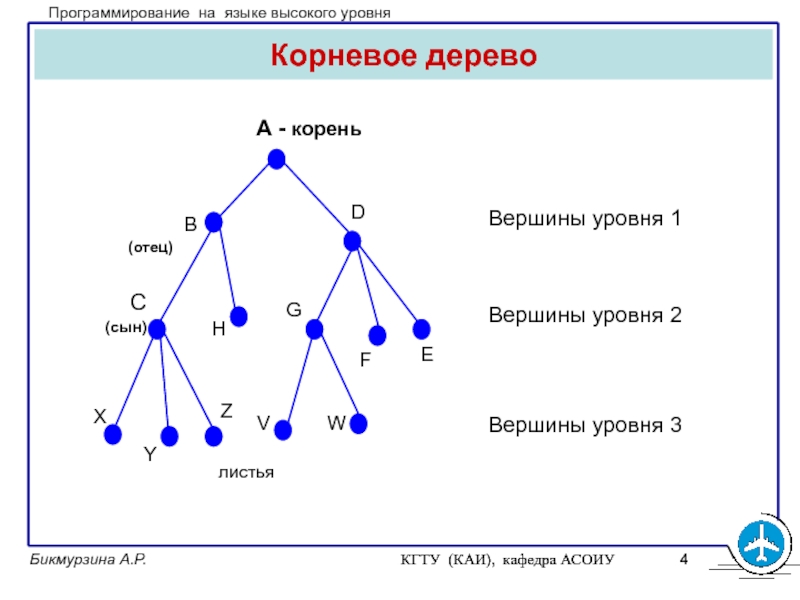
Уровень вершины
определяется расстоянием вершины от корня. Высота дерева – это максимальный
уровень его вершин.Преемников вершины называют сыновьями, а предшественника – родителем или отцом.
Степень вершины – число ее сыновей. Вершины без сыновей называют терминальными или листьями. Дуги называют ветвями.
Слайд 4КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Корневое дерево
Вершины
уровня 1
Вершины уровня 2
Вершины уровня 3
А - корень
листья
D
E
F
G
H
Y
Z
V
X
W
Слайд 5КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Примеры деревьев
Структура организации
и ее подразделений.
Родословное дерево.
Структура книги, состоящей из разделов и подразделов.
Структура
сложной программы, где корень дерева – главная функция, вершины 1-го уровня – подпрограммы, вызываемые из главной функции и т.д.Слайд 6КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
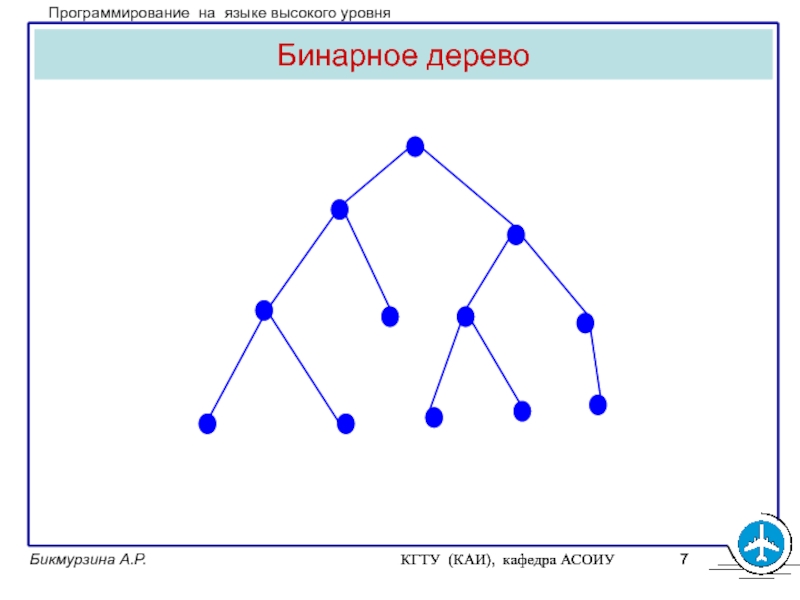
Дерево называется
упорядоченным, если сыновья каждой вершины упорядочены каким-либо образом.
Бинарное (двоичное) дерево
– упорядоченное дерево степени 2: каждая вершина имеет не более 2-х сыновей, образующих корни ее левого и правого поддерева.Слайд 8КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Представление деревьев
Деревья
чаще всего хранят в виде сетей или списковых структур.
Каждый элемент
сети содержит номер или метку вершины и указатели на элементы-сыновья.В регулярной (однородной) сети число указателей у элементов одинаковое, а в нерегулярной сети – разное.
Слайд 10КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
Пример. Использование бинарного
дерева для сортировки данных
Допустим дана последовательность чисел, например:
15 10
20 12 8 17 25 5 9Вывести числа в порядке возрастания:
5 8 9 10 12 15 17 20 25
Слайд 11КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
Построим
бинарное дерево: первое число будет корнем дерева. Если второе число
< 1-го, то оно станет корнем левого поддерева, а если > 1-го, то станет корнем правого поддерева. Каждое следующее число будет добавляться либо в левое поддерево, либо в правое.Слайд 12КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
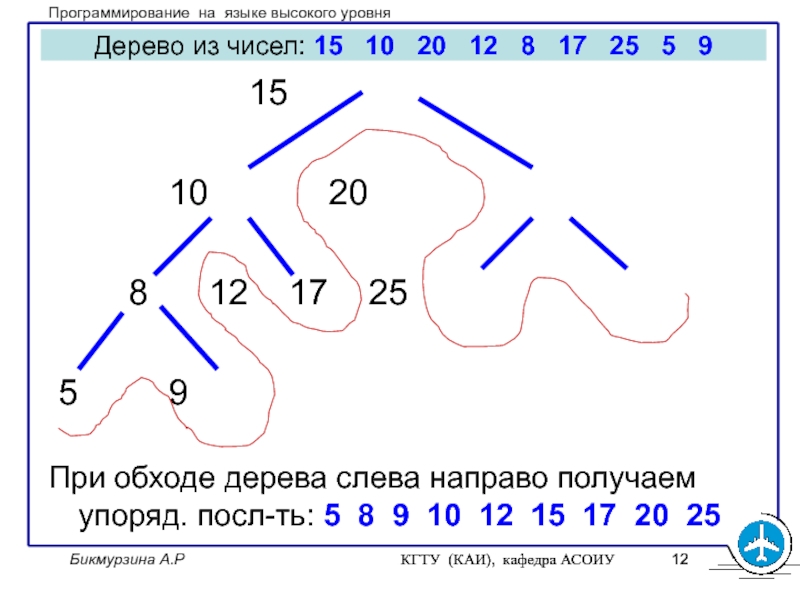
Дерево из чисел:
15 10 20 12 8
17 25 5 9 15
10 20
8 12 17 25
5 9
При обходе дерева слева направо получаем упоряд. посл-ть: 5 8 9 10 12 15 17 20 25
Слайд 13КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
Алгоритм
1. Создание бинарного
дерева в виде регулярной сети.
2. Обход дерева слева направо и
вывод меток его вершин (чисел).3. Удаление дерева (освобождение памяти).
Слайд 14КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
Программа
#include
#include
/*
Описание бинарного дерева в виде регулярной сети */
// Тип вершины
дерева (элемента сети) struct TREE
{ float number; // число
TREE *left, *right; /* указатели на левое и правое поддеревья*/
};
Слайд 15КГТУ (КАИ), кафедра АСОИУ
// Прототипы функций
void insert (TREE *pt,
float x);
void print_tree (TREE *pt);
void delete_tree (TREE *pt);
Слайд 16КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
/*--------------------------------------*/
/*
Главная функция */
/*--------------------------------------*/
void main()
{ TREE *pt;
// указатель на корень дерева float x; // очередное число
puts ("\nВведите числовую последовательность");
scanf("%f", &x);
// создание корня дерева
pt = (TREE *) malloc (sizeof(TREE));
pt->number=x;
pt->left=pt->right=NULL;
Слайд 17КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
// ввод чисел и формирование дерева while (scanf("%f", &x) !=
EOF)insert (pt,x);
// обход дерева и печать результата
puts ("Результат:");
print_tree (pt);
// удаление дерева
delete_tree (pt);
}
Слайд 18КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
/*--------------------------------------------------------------------------*/
/* Функция
включения новой вершины в дерево */
/*--------------------------------------------------------------------------*/
void insert (TREE *pt,
float x)// pt - указатель на корень дерева
// x – число - метка новой вершины
{ TREE *i; /* указатель на текущую вершину дерева */
TREE *parent; /* указатель на вершину- родителя для новой вершины */
int dir; /* признак включения новой вершины
в левую или правую ветвь */
Слайд 19КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
/*
спуск по дереву и поиск вершины- родителя для новой вершины*/
i = pt;while (i != NULL)
{ parent = i;
if (x < i->number) { // спуск влево i = i->left; dir = 0;
}
else { // спуск вправо
i = i->right; dir = 1;
}
}
Слайд 20КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
/*
создание новой вершины */
i = (TREE *) malloc
(sizeof (TREE));i->number = x;
i->left = i->right = NULL;
/* включение новой вершины в левую или правую ветвь родителя*/
if (dir == 0) parent->left = i;
else parent->right = i;
}
Слайд 21КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
/*---------------------------------------------------------------------*/
/* Рекурсивная
функция обхода дерева слева */
/* направо
и печати его вершин *//*---------------------------------------------------------------------*/
void print_tree (TREE *pt)
/* pt - указатель на корень дерева (поддерева) */
{ if (pt)
{ print_tree (pt->left);
printf ("%f ", pt->number);
print_tree (pt->right);
}
}
Слайд 22КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
/*-----------------------------------------------------------------*/
/* Рекурсивная
функция обхода дерева снизу */
/*
вверх и удаления его вершин *//*-----------------------------------------------------------------*/
void delete_tree (TREE *pt)
// pt - указатель на корень дерева (поддерева)
{ if (pt)
{ delete_tree (pt->left);
delete_tree (pt->right);
free (pt);
}
}
Слайд 23КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р
КГТУ (КАИ), кафедра АСОИУ
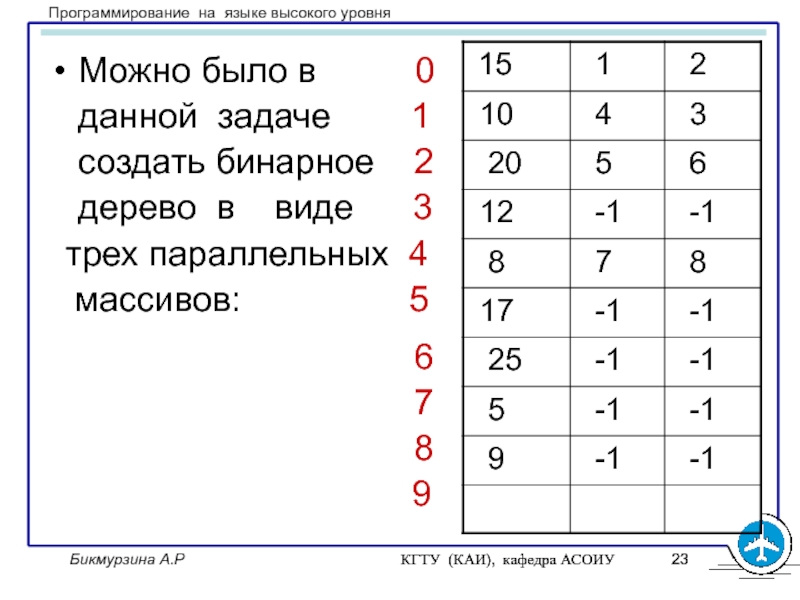
Можно было
в 0
данной задаче
1создать бинарное 2
дерево в виде 3
трех параллельных 4
массивов: 5
6
7
8
9
Слайд 24КГТУ (КАИ), кафедра АСОИУ
Три способа обхода бинарного дерева
Прямой обход
(обход сверху вниз):
1. Корень
2. Левое поддерево
3. Правое поддерево
Внутренний обход (обход слева направо): 1. Левое поддерево 2. Корень 3. Правое поддерево
Обратный обход (обход снизу вверх):
1. Левое поддерево 2. Правое поддерево 3. Корень
Бикмурзина А.Р
Слайд 25КГТУ (КАИ), кафедра АСОИУ
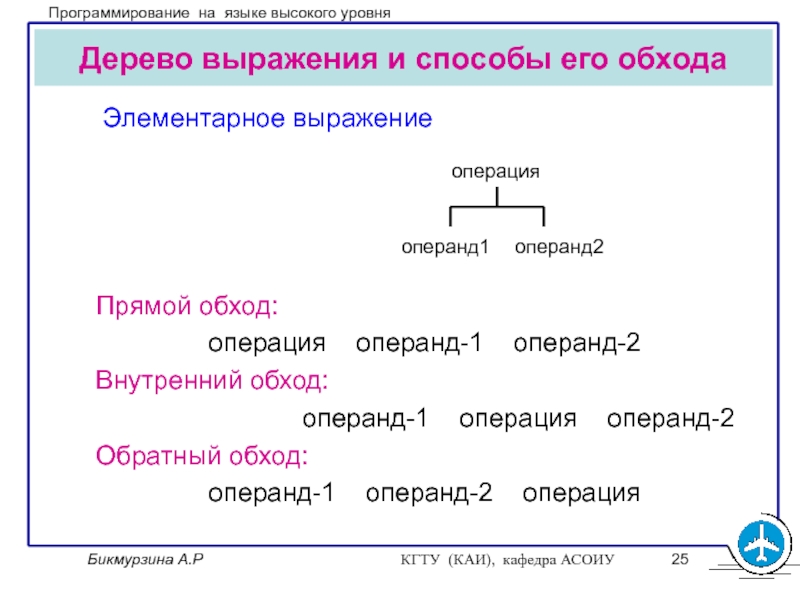
Дерево выражения и способы его обхода
Элементарное
выражение
Прямой обход:
операция операнд-1 операнд-2
Внутренний обход:
операнд-1 операция операнд-2
Обратный обход:
операнд-1 операнд-2 операция
Бикмурзина А.Р
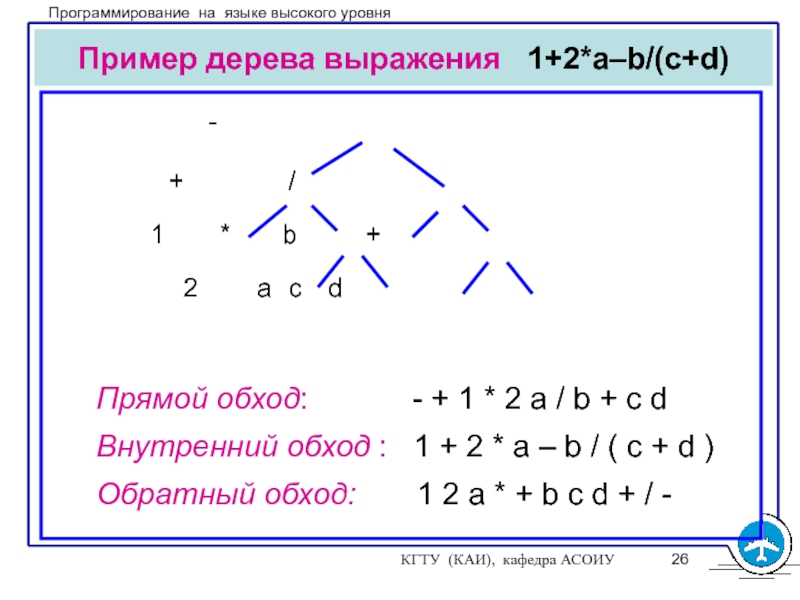
Слайд 26КГТУ (КАИ), кафедра АСОИУ
Пример дерева выражения 1+2*a–b/(c+d)
-
+
/
1 *
b +2 a c d
Прямой обход: - + 1 * 2 a / b + c d
Внутренний обход : 1 + 2 * a – b / ( c + d )
Обратный обход: 1 2 a * + b c d + / -
Слайд 27КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Древовидные таблицы
Древовидная таблица
(дерево поиска) – это бинарное дерево, в котором вершины соответствуют
элементам таблицы.Ключ каждой вершины больше ключей ее левого поддерева и меньше ключей правого поддерева.
Ключи могут быть любого типа (сравниваются их числовые коды).
Слайд 28КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Пример
База данных содержит
сведения о владельцах автомобилей. Необходимо по номерам машин устанавливать их
владельцев.Для более быстрого поиска можно построить древовидную таблицу, где ключом элемента будет номер автомобиля. Каждый элемент таблицы будет содержать ключ, тело и два указателя на левое и правое поддеревья. У левого поддерева ключи будут < чем у корня, а у правого >.
Слайд 29КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Описание таблицы в
виде сети (С++)
// структура элемента
struct AVTO
{ char number[12]; //
номер автомобиляchar fam[30]; // фамилия, имя, отчество
char date[9]; // дата техосмотра
AVTO *left, *right; /* указатели на левое и правое поддеревья */
};
AVTO *pt; /* указатель таблицы (на корень дерева) */
Слайд 30КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
/* Функция поиска
элемента по ключу */
AVTO * Search (AVTO *pt, char number[])
/* Вх.
данные: pt – указатель таблицы,number – ключ - номер автомобиля */
/* Функция возвращает адрес найденного элемента или NULL, если элемента нет в таблице */
{ AVTO *i = pt; /* указатель на очередной элемент таблицы */
Слайд 31КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
while (i
&& strcmp (number, i ->number))
{ if (strcmp (number, i
->number)<0)i = i -> left;
else i = i -> right;
}
return i;
}
Слайд 32КГТУ (КАИ), кафедра АСОИУ
Бикмурзина А.Р.
КГТУ (КАИ), кафедра АСОИУ
Пример вызова функции
char num[12]; // искомый номер автомобиля
AVTO *p;
// указатель на найденный элементputs (“Введите номер”);
gets (num);
if (p = Search(pt, num))
printf (“Владелец: %s, дата техосмотра: %s”,
p -> fam, p -> date );
else puts (“Данного номера нет в базе данных”);

























![Лекции 13-14 КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра АСОИУПример вызова функции char КГТУ (КАИ), кафедра АСОИУБикмурзина А.Р.КГТУ (КАИ), кафедра АСОИУПример вызова функции char num[12]; // искомый номер](/img/thumbs/726e4bf11d84c21969b5cc5ffc9c788d-800x.jpg)



















