Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 0
Содержание
- 1. Лекция 0
- 2. История термина «Алгоритм»Алгори́тм, от имени учёного аль-Хорезми
- 3. История термина «Алгоритм»Современное формальное определение алгоритма было
- 4. Различные определения«Алгоритм — это конечный набор правил, который
- 5. Формальные свойства алгоритмов Различные определения алгоритма в
- 6. Формальные свойства алгоритмов Понятность — алгоритм для
- 7. Исполнитель алгоритма — это некоторая абстрактная или
- 8. Исполнитель алгоритмаСpеда (или обстановка) — это "место
- 9. Обычно исполнитель ничего не знает о цели
- 10. Формы записи алгоритмовсловесная (запись на естественном языке);
- 11. Формы записи алгоритмовСловесный способ записи алгоритмов представляет
- 12. Пример словесного алгоритмаЗаписать алгоритм нахождения наибольшего общего
- 13. Пример словесного алгоритмаОписанный алгоритм применим к любым
- 14. Графический способ записи алгоритмов При графическом представлении
- 15. Графический способ записи алгоритмов Графическое представление называется
- 16. Графический способ записи алгоритмов
- 17. Графический способ записи алгоритмов
- 18. Графический способ записи алгоритмовБлок "процесс" применяется для
- 19. Способ записи алгоритмов в виде псевдокода Псевдокод
- 20. Способ записи алгоритмов в виде псевдокода В
- 21. Пример использования псевдокода (школьный алгоритмический язык )
- 22. Пример использования псевдокода (школьный алгоритмический язык )
- 23. Базовые алгоритмические структуры Логическая структура любого алгоритма
- 24. Базовые алгоритмические структуры 1. Базовая структура "следование". Образуется последовательностью действий, следующих одно за другим:
- 25. Базовые алгоритмические структуры Базовая структура "ветвление". Обеспечивает
- 26. Базовые алгоритмические структуры
- 27. Базовые алгоритмические структуры 3. Базовая структура "цикл".
- 28. Базовые алгоритмические структуры
- 29. Пример цикла с постусловиемВывести все натуральные числа меньше 10.Условие:
- 30. Набор действий для цикла с постусловием:Первый шаг:Начальное
- 31. Набор действий для цикла с предусловием:Первый шаг:Начальное
- 32. Набор действий для цикла с типа ДЛЯ:ЦИКЛ
- 33. Циклы с условиямиВывести значения координат ломанной линии с изломом в точке 100:0,5*x, если x100
- 34. Набор действий для цикла с предусловием:Первый шаг:Начальное
- 35. Циклы с условиямиВывести значения координат ломанной линии
- 36. Набор действий для цикла с предусловием:Первый шаг:Начальное
- 37. Итерационные циклыВ итерационных циклах число повторений операторов
- 38. Итерационные циклыПример. Составить алгоритм вычисления бесконечной суммы
- 39. Итерационные циклыРешая эту задачу "в лоб" путем
- 40. Итерационные циклы
- 41. Вложенные циклы Возможны случаи, когда внутри тела
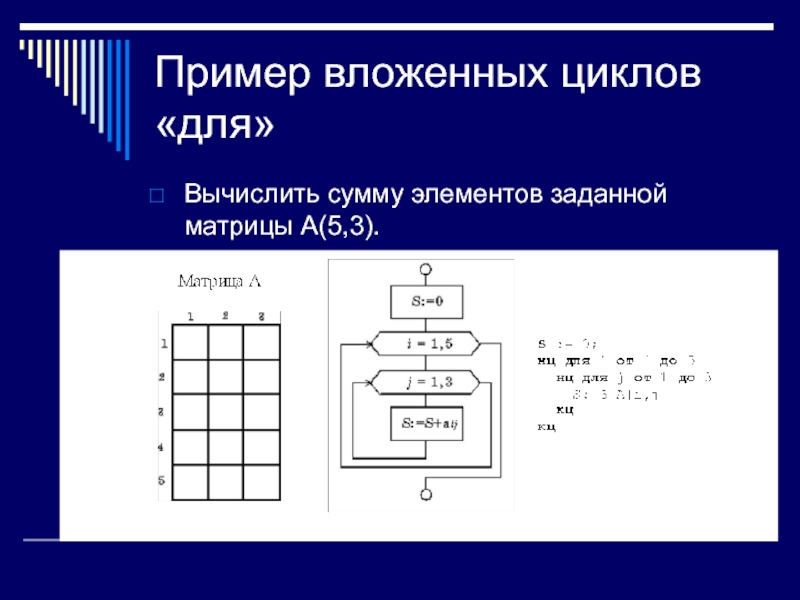
- 42. Пример вложенных циклов «для» Вычислить сумму элементов заданной матрицы А(5,3).
- 43. Пример вложенных циклов «пока» Вычислить произведение
- 44. Программный способ записи алгоритмов При записи алгоритма
- 45. Уровень языка программирования В настоящее время в
- 46. Уровень языка программирования Машинные языки и машинно-ориентированные
- 47. Уровень языка программирования Языки высокого уровня делятся
- 48. Алгоритмический язык Алгоритмический язык (как и любой другой язык) образуют три его составляющие:алфавит,синтаксис,семантика.
- 49. Алгоритмический язык Алфавит — это фиксированный для
- 50. Стандартная функция Вычисления часто употребляемых функций осуществляются
- 51. Стандартная функция Вычисления часто употребляемых функций осуществляются
- 52. Стандартная функция (примеры)
- 53. Создание пользовательских процедур и функцийВ любом языке
- 54. Создание пользовательских процедур и функцийНапример, в языке
- 55. Создание пользовательских процедур и функцийФормат описания процедуры
- 56. Создание пользовательских процедур и функцийФормат описания функции:
- 57. Создание пользовательских процедур и функцийФормальные параметры в
- 58. Создание пользовательских процедур и функцийProgram Zad3 (mai,
- 59. Запись арифметических выражений Арифметические выражения записываются по
- 60. Запись арифметических выражений
- 61. Запись арифметических выражений Типичные ошибки в записи
- 62. Теперь можно перейти к практике!!!Найти лектора можно
- 63. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2История термина «Алгоритм»
Алгори́тм, от имени учёного аль-Хорезми (перс. خوارزمی [al-Khwārazmī]) —
Слайд 3История термина «Алгоритм»
Современное формальное определение алгоритма было дано в 30—50-х
годы XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча —
Тьюринга), Н. Винера, А. А. Маркова.ЕДИНОГО «ИСТИННОГО» ОПРЕДЕЛЕНИЯ ПОНЯТИЯ «АЛГОРИТМ» НЕТ.
Слайд 4Различные определения
«Алгоритм — это конечный набор правил, который определяет последовательность операций
для решения конкретного множества задач и обладает пятью важными чертами:
конечность, определённость, ввод, вывод, эффективность». (Д. Э. Кнут)«Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи». (А. Колмогоров)
«Алгоритм — это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату». (А. Марков)
«Алгоритм — точное предписание о выполнении в определённом порядке некоторой системы операций, ведущих к решению всех задач данного типа». (Философский словарь / Под ред. М. М. Розенталя)
«Алгоритм — строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд». (Николай Дмитриевич Угринович, учебник «Информатика и информационные технологии»)
Слайд 5Формальные свойства алгоритмов
Различные определения алгоритма в явной или неявной
форме содержат следующий ряд общих требований:
Дискретность — алгоритм должен представлять
процесс решения задачи как последовательное выполнение некоторых простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, то есть преобразование исходных данных в результат осуществляется во времени дискретно.Детерминированность (определённость). В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф.
Слайд 6Формальные свойства алгоритмов
Понятность — алгоритм для исполнителя должен включать
только те команды, которые ему (исполнителю) доступны, которые входят в
его систему команд.Завершаемость (конечность) — при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов. С другой стороны, вероятностный алгоритм может и никогда не выдать результат, но вероятность этого равна 0.
Массовость (универсальность). Алгоритм должен быть применим к разным наборам исходных данных.
Результативность — завершение алгоритма определёнными результатами.
Алгоритм содержит ошибки, если приводит к получению неправильных результатов либо не даёт результатов вовсе.
Алгоритм не содержит ошибок, если он даёт правильные результаты для любых допустимых исходных данных.
Слайд 7Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, биологическая
или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.
Слайд 8Исполнитель алгоритма
Сpеда (или обстановка) — это "место обитания" исполнителя. Напpимеp,
для исполнителя Pобота из школьного учебника [1] сpеда — это
бесконечное клеточное поле. Стены и закpашенные клетки тоже часть сpеды. А их pасположение и положение самого Pобота задают конкpетное состояние среды.Система команд. Каждый исполнитель может выполнять команды только из некотоpого стpого заданного списка — системы команд исполнителя. Для каждой команды должны быть заданы условия пpименимости (в каких состояниях сpеды может быть выполнена команда) и описаны pезультаты выполнения команды. Напpимеp, команда Pобота "ввеpх" может быть выполнена, если выше Pобота нет стены. Ее pезультат — смещение Pобота на одну клетку ввеpх.
После вызова команды исполнитель совеpшает соответствующее элементаpное действие.
Отказы исполнителя возникают, если команда вызывается пpи недопустимом для нее состоянии сpеды.
Слайд 9Обычно исполнитель ничего не знает о цели алгоpитма. Он выполняет
все полученные команды, не задавая вопросов "почему" и "зачем".
В
информатике универсальным исполнителем алгоритмов является компьютер. Слайд 10Формы записи алгоритмов
словесная (запись на естественном языке);
графическая (изображения из
графических символов);
псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке,
включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.); программная (тексты на языках программирования).
Слайд 11Формы записи алгоритмов
Словесный способ записи алгоритмов представляет собой описание последовательных
этапов обработки данных. Алгоритм задается в произвольном изложении на естественном
языке.Слайд 12Пример словесного алгоритма
Записать алгоритм нахождения наибольшего общего делителя (НОД) двух
натуральных чисел (алгоритм Эвклида).
Алгоритм может быть следующим:
задать два
числа; если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
определить большее из чисел;
заменить большее из чисел разностью большего и меньшего из чисел;
повторить алгоритм с шага 2.
Слайд 13Пример словесного алгоритма
Описанный алгоритм применим к любым натуральным числам и
должен приводить к решению поставленной задачи.
Недостатки:
Словесный способ не имеет
широкого распространения, так как такие описания: строго не формализуемы;
страдают многословностью записей;
допускают неоднозначность толкования отдельных предписаний.
Слайд 14Графический способ записи алгоритмов
При графическом представлении алгоритм изображается в
виде последовательности связанных между собой функциональных блоков, каждый из которых
соответствует выполнению одного или нескольких действий.Слайд 15Графический способ записи алгоритмов
Графическое представление называется схемой алгоритма или
блок-схемой.
В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений
выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа.Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.
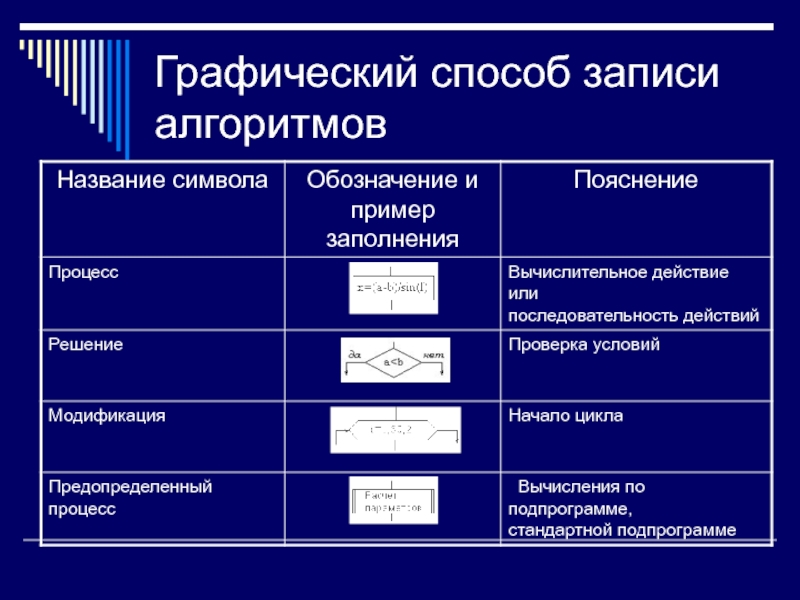
Слайд 18Графический способ записи алгоритмов
Блок "процесс" применяется для обозначения действия или
последовательности действий, изменяющих значение, форму представления или размещения данных. Для
улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.Блок "решение" используется для обозначения переходов управления по условию. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок "модификация" используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок "предопределенный процесс" используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Слайд 19Способ записи алгоритмов в виде псевдокода
Псевдокод представляет собой систему
обозначений и правил, предназначенную для единообразной записи алгоритмов.
Псевдокод занимает
промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой строны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. Слайд 20Способ записи алгоритмов в виде псевдокода
В псевдокоде не приняты
строгие синтаксические правила для записи команд, присущие формальным языкам, что
облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Слайд 22Пример использования псевдокода (школьный алгоритмический язык )
алг название алгоритма
(аргументы и результаты)
дано условия применимости алгоритма
надо цель выполнения
алгоритманач описание промежуточных величин | последовательность команд (тело алгоритма)
кон
Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон — телом алгоритма.
Слайд 23Базовые алгоритмические структуры
Логическая структура любого алгоритма может быть
представлена
комбинацией трех базовых структур:
следование, ветвление, цикл.
Слайд 24Базовые алгоритмические структуры
1. Базовая структура "следование". Образуется последовательностью действий,
следующих одно за другим:
Слайд 25Базовые алгоритмические структуры
Базовая структура "ветвление". Обеспечивает в зависимости от
результата проверки условия (да или нет) выбор одного из альтернативных
путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Структура ветвление существует в четырех основных вариантах:если—то;
если—то—иначе;
выбор;
выбор—иначе.
Слайд 27Базовые алгоритмические структуры
3. Базовая структура "цикл". Обеспечивает многократное выполнение
некоторой совокупности действий, которая называется телом цикла. Основные разновидности циклов
представлены в таблице:Слайд 29Пример цикла с постусловием
Вывести все натуральные числа меньше 10.
Условие:
натуральные
Набор действий
Слайд 30Набор действий для цикла с постусловием:
Первый шаг:
Начальное значение => Х:=9;
Второй шаг:
Вывести Х => write(x);
Третий шаг
Уменьшаем Х на 1 =>
X:=X-1; (dec(x);)Проверка конца работы
Число натуральное? => x>0
Цикл
Если х>0, перейти к второму шагу, иначе перейти на Конец
Конец
Слайд 31Набор действий для цикла с предусловием:
Первый шаг:
Начальное значение => Х:=9;
Второй шаг:
Число натуральное? => x>0; (если не натуральное в конец)
Третий
шагВывести Х => write(x);
Четвёртый шаг
Уменьшаем Х на 1 => X:=X-1; (dec(x);)
Пятый шаг
Перейти к второму шагу
Конец
Слайд 33Циклы с условиями
Вывести значения координат ломанной линии с изломом в
точке 100:
0,5*x, если x100
Слайд 34Набор действий для цикла с предусловием:
Первый шаг:
Начальное значение Х =>
Х:=0;
Второй шаг
Условие излома => x
шагу Три иначе к шагу ЧетыреТретий шаг
Вычислить f(x) => y:=0.5*x;
Идти на пункт Конец цикла
Четвёртый шаг
Вычислить f(x) => y:=2*x;
Идти на пункт Конец цикла
Конец цикла
Вывести x -> f(x)
Увеличить х
Х в диапазоне => x<199
Если условие истина перейти к шагу Два иначе к Конец программы
Конец программыё
Слайд 35Циклы с условиями
Вывести значения координат ломанной линии с изломом в
точках 5 и 15:
0, если x15
f(x)=
10, если x>=5
и x<=15Слайд 36Набор действий для цикла с предусловием:
Первый шаг:
Начальное значение Х =>
Х:=0;
Второй шаг
Условие излома => x>=5 и x
перейти к шагу Три иначе к шагу ЧетыреТретий шаг
Вычислить f(x) => y:=10;
Идти на пункт Конец цикла
Четвёртый шаг
Вычислить f(x) => y:= 0;
Идти на пункт Конец цикла
Конец цикла
Вывести x -> f(x)
Увеличить х
Х в диапазоне => x<=20
Если условие истина перейти к шагу Два иначе к Конец программы
Конец программыё
Слайд 37Итерационные циклы
В итерационных циклах число повторений операторов тела цикла заранее
неизвестно. Для его организации используется цикл типа пока .
Выход из итерационного цикла осуществляется в случае выполнения заданного условия.На каждом шаге вычислений происходит последовательное приближение к искомому результату и проверка условия достижения последнего.
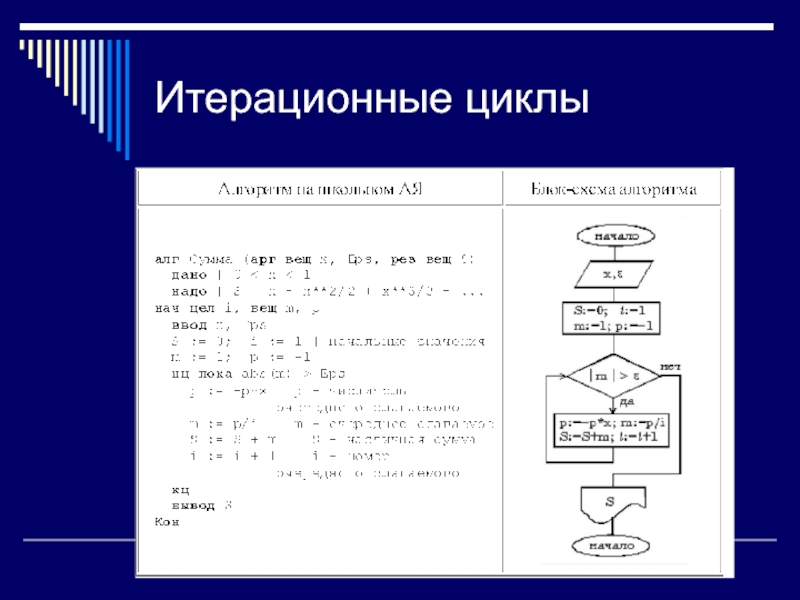
Слайд 38Итерационные циклы
Пример. Составить алгоритм вычисления бесконечной суммы
с заданной точностью
(для данной знакочере-дующейся бесконечной суммы требуемая точность будет достигнута,
когда очередное слагаемое станет по абсолютной величине меньше ).Слайд 39Итерационные циклы
Решая эту задачу "в лоб" путем вычисления на каждом
i-ом шаге частичной суммы
S:=S + ((-1)**(i-1)) * (x**i)
/ i ,мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р , то у следующего слагаемого числитель будет равен —р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m будет равно p/i , где i — номер слагаемого.
Слайд 41Вложенные циклы
Возможны случаи, когда внутри тела цикла необходимо повторять
некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура
получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.
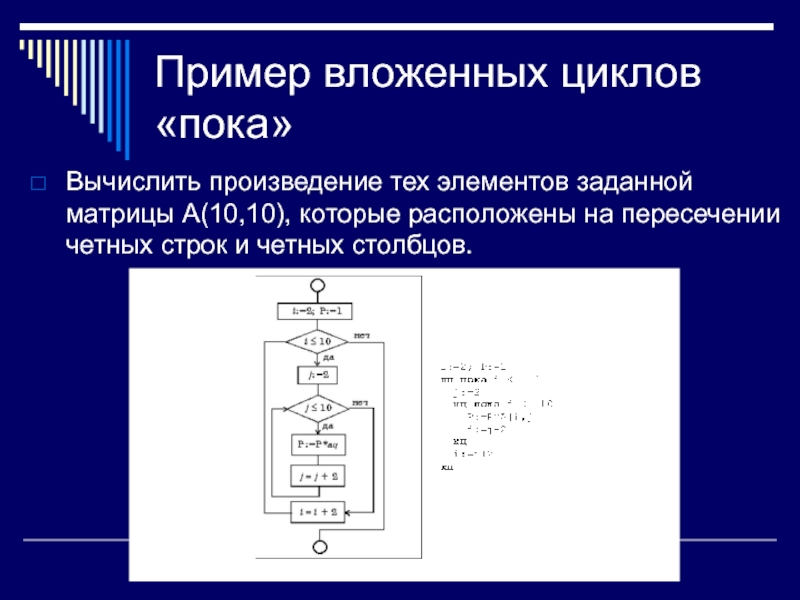
Слайд 43Пример вложенных циклов «пока»
Вычислить произведение тех элементов заданной
матрицы A(10,10), которые расположены на пересечении четных строк и четных
столбцов.Слайд 44Программный способ записи алгоритмов
При записи алгоритма в словесной форме,
в виде блок-схемы или на псевдокоде допускается определенная произвольность при
изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм.Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы — компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем.
Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке — программой для компьютера.
Слайд 45Уровень языка программирования
В настоящее время в мире существует несколько
сотен реально используемых языков программирования. Для каждого есть своя область
применения.Любой алгоритм, как мы знаем, есть последовательность предписаний, выполнив которые можно за конечное число шагов перейти от исходных данных к результату. В зависимости от степени детализации предписаний обычно определяется уровень языка программирования — чем меньше детализация, тем выше уровень языка.
По этому критерию можно выделить следующие уровни языков программирования:
машинные;
машинно-оpиентиpованные (ассемблеpы);
машинно-независимые (языки высокого уровня).
Слайд 46Уровень языка программирования
Машинные языки и машинно-ориентированные языки — это
языки низкого уровня, требующие указания мелких деталей процесса обработки данных.
Языки же высокого уровня имитируют естественные языки, используя некоторые слова разговорного языка и общепринятые математические символы. Эти языки более удобны для человека.Слайд 47Уровень языка программирования
Языки высокого уровня делятся на:
процедурные (алгоритмические)
(Basic, Pascal, C и др.), которые предназначены для однозначного описания
алгоритмов; для решения задачи процедурные языки требуют в той или иной форме явно записать процедуру ее решения;логические (Prolog, Lisp и др.), которые ориентированы не на разработку алгоритма решения задачи, а на систематическое и формализованное описание задачи с тем, чтобы решение следовало из составленного описания;
объектно-ориентированные (Object Pascal, Java, C++, C# и др.), в основе которых лежит понятие объекта, сочетающего в себе данные и действия над ними. Программа на объектно-ориентированном языке, решая некоторую задачу, по сути описывает часть мира, относящуюся к этой задаче. Описание действительности в форме системы взаимодействующих объектов естественнее, чем в форме взаимодействующих процедур.
Слайд 48Алгоритмический язык
Алгоритмический язык (как и любой другой язык) образуют
три его составляющие:
алфавит,
синтаксис,
семантика.
Слайд 49Алгоритмический язык
Алфавит — это фиксированный для данного языка набор
основных символов, т.е. "букв алфавита", из которых должен состоять любой
текст на этом языке — никакие другие символы в тексте не допускаются.Синтаксис — это правила построения фраз, позволяющие определить, правильно или неправильно написана та или иная фраза. Точнее говоря, синтаксис языка представляет собой набор правил, устанавливающих, какие комбинации символов являются осмысленными предложениями на этом языке.
Семантика определяет смысловое значение предложений языка. Являясь системой правил истолкования отдельных языковых конструкций, семантика устанавливает, какие последовательности действий описываются теми или иными фразами языка и, в конечном итоге, какой алгоритм определен данным текстом на алгоритмическом языке.
Слайд 50Стандартная функция
Вычисления часто употребляемых функций осуществляются посредством подпрограмм, называемых
стандартными функциями, которые заранее запрограммированы и встроены в транслятор языка.
Слайд 51Стандартная функция
Вычисления часто употребляемых функций осуществляются посредством подпрограмм, называемых
стандартными функциями, которые заранее запрограммированы и встроены в транслятор языка.
Слайд 53Создание пользовательских процедур и функций
В любом языке программирования предусмотрены средства,
позволяющие оформлять вспомогательный алгоритм как подпрограмму.
Для использования подалгоритма в
качестве подпрограммы ему необходимо присвоить имя и описать алгоритм по правилам языка. В дальнейшем, при необходимости вызвать его в программе, делают вызов подпрограммы упоминанием в нужном месте имени соответствующего подалгоритма со списком входных и выходных данных.Слайд 54Создание пользовательских процедур и функций
Например, в языке Паскаль имеется два
вида подпрограмм - процедуры и функции.
Процедуры и функции помещаются
в раздел описаний программы. Для обмена информацией между процедурами и функциями и другими блоками программы существует механизм входных и выходных параметров. Входными параметрами называют величины, передающиеся из вызывающего блока в подпрограмму (исходные данные), а выходными - передающиеся из подпрограммы в вызывающий блок (результаты работы подпрограммы).
Слайд 55Создание пользовательских процедур и функций
Формат описания процедуры имеет вид:
procedure
имя процедуры (формальные параметры);
раздел описаний процедуры
begin
исполняемая часть процедуры
end;
Слайд 56Создание пользовательских процедур и функций
Формат описания функции:
function имя функции
(формальные параметры):тип результата;
раздел описаний функции
begin
исполняемая часть функции
end;
Слайд 57Создание пользовательских процедур и функций
Формальные параметры в заголовке процедур и
функций записываются в виде:
var имя праметра: имя типа
Вызов процедуры
производится оператором, имеющим следующий формат: имя процедуры(список фактических параметров);
Слайд 58Создание пользовательских процедур и функций
Program Zad3 (mai, max);
Uses crt;
const N=10; {размерность
массива }
var
fi: array [1..N] of integer; { описание
массива }i: integer;
min_i,max_i,min,max: integer;
procedure Min_Max;
var i: integer;
begin
for i := 2 to N do
begin
if fi[i] > max then
begin
max:= fi[i];
max_i:=i;
end;
if fi[i] < min then
begin
min:= fi[i];
min_i:=i;
end;end;
write('index Minimal element = ',min_i);
write('index Maximal element =',max_i);
end;
begin
clrscr;
writeln ('введите массив размерностью N элементов');
for i:= 1 to N do {ввод элементов массива }
read(fi[i]);
min:=fi[1]; max:=fi[1];
min_i:=1; max_i:=1;
min_max;
end.
Слайд 59Запись арифметических выражений
Арифметические выражения записываются по следующим правилам:
Нельзя
опускать знак умножения между сомножителями и ставить рядом два знака
операций.Индексы элементов массивов записываются в квадратных (школьный АЯ, Pascal) или круглых (Basic) скобках.
Для обозначения переменных используются буквы латинского алфавита.
Операции выполняются в порядке старшинства: сначала вычисление функций, затем возведение в степень, потом умножение и деление и в последнюю очередь — сложение и вычитание.
Операции одного старшинства выполняются слева направо. Однако, в школьном АЯ есть одно исключение из этого правила: операции возведения в степень выполняются справа налево. Так, выражение 2**(3**2) в школьном АЯ вычисляется как 2**(3**2) = 512. В языке QBasic аналогичное выражение 2^3^2 вычисляется как (2^3)^2 = 64. А в языке Pascal вообще не предусмотрена операция возведения в степень, в Pascal x^y записывается как exp(y*ln(x)), а x^y^z как exp(exp(z*ln(y))*ln(x)).
Слайд 61Запись арифметических выражений
Типичные ошибки в записи выражений:
5x +
1 (пропущен знак умножения между 5 и х)
a + sin
x (аргумент x функции sin x не заключен в скобки)((a + b)/c**3 (не хватает закрывающей скобки)

![Лекция 0 История термина «Алгоритм»Алгори́тм, от имени учёного аль-Хорезми (перс. خوارزمی [al-Khwārazmī]) — точный История термина «Алгоритм»Алгори́тм, от имени учёного аль-Хорезми (перс. خوارزمی [al-Khwārazmī]) — точный набор инструкций, описывающих порядок действий исполнителя](/img/thumbs/900e17c4bea59c1bcd7c113b2af62457-800x.jpg)



















































![Лекция 0 Создание пользовательских процедур и функцийProgram Zad3 (mai, max);Uses crt;const N=10; {размерность массива Создание пользовательских процедур и функцийProgram Zad3 (mai, max);Uses crt;const N=10; {размерность массива }varfi: array [1..N] of integer;](/img/thumbs/7f2c30af01a81e598ab64f11c42a80d9-800x.jpg)






















