и потенциал:
- равномерно заряженного шара;
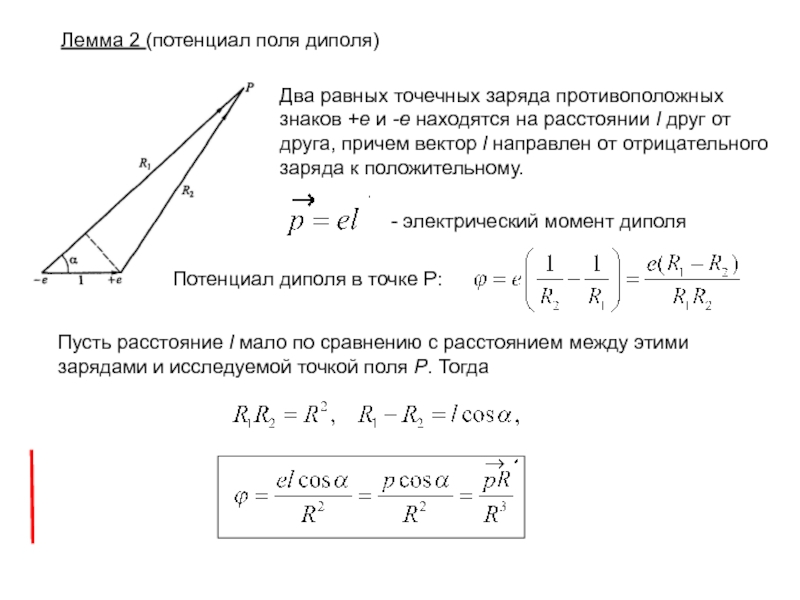
- одиночного диполя;
- равномерно поляризованного
шара;Поглощение и отражение света колебаниями решетки
2. Локальное поле, действующее на отдельный диполь в диэлектрике