Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 1 3. Возрастание, убывание функций, необходимые и достаточные условия
Содержание
- 1. Лекция 1 3. Возрастание, убывание функций, необходимые и достаточные условия
- 2. § 1.Условия постоянства и монотонности функции. Теорема
- 3. Доказательство« » Это известно из предыдущего.
- 4. На отрезке [x1 ; x2] функция удовлетворяет
- 5. Теорема (достаточные условия монотонности). Пусть x
- 6. Доказательство1 часть. f (x) > 0 на
- 7. 2 часть. Возьмём произвольную пару точек x1,
- 8. § 2. Полное исследование функций и построение
- 9. Алгоритм исследования функции:1) О.Д.З. D( f )
- 10. 6) Вычисление значений функции в некоторых характерных
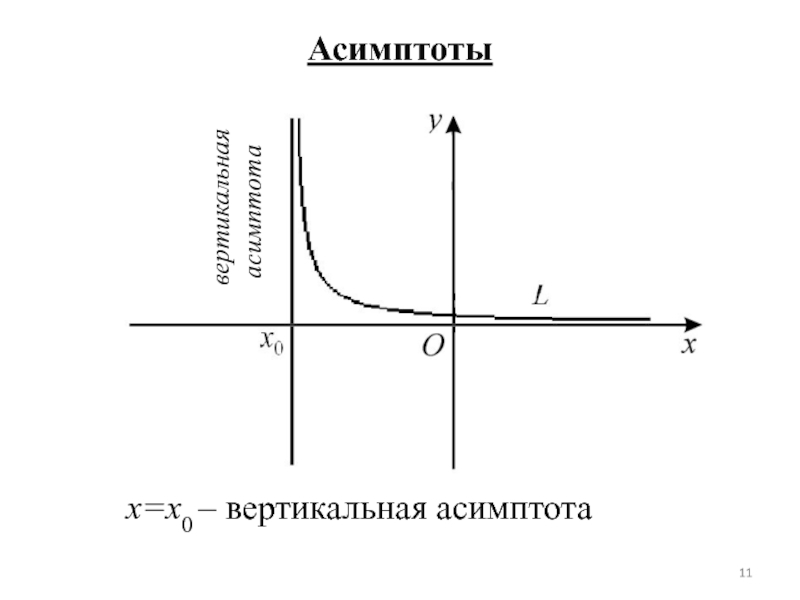
- 11. Асимптотыx=x0 – вертикальная асимптотавертикальная асимптота
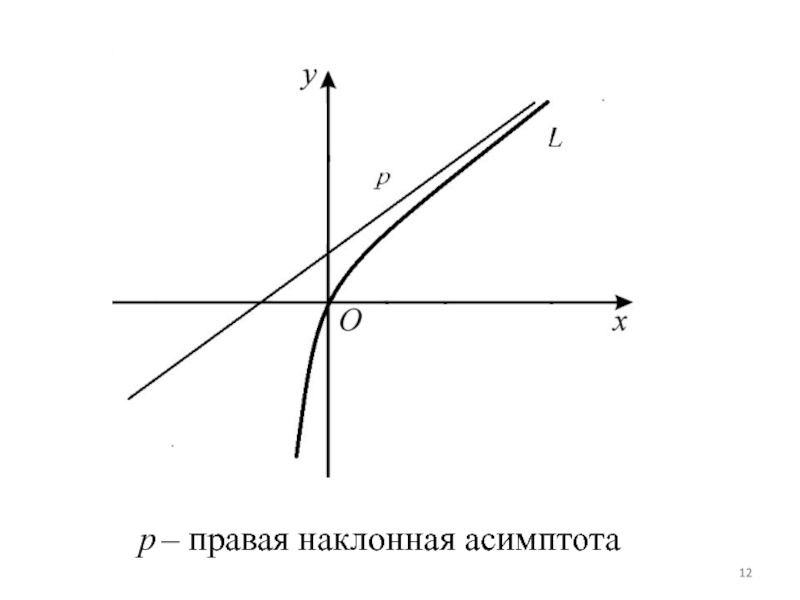
- 12. p – правая наклонная асимптота
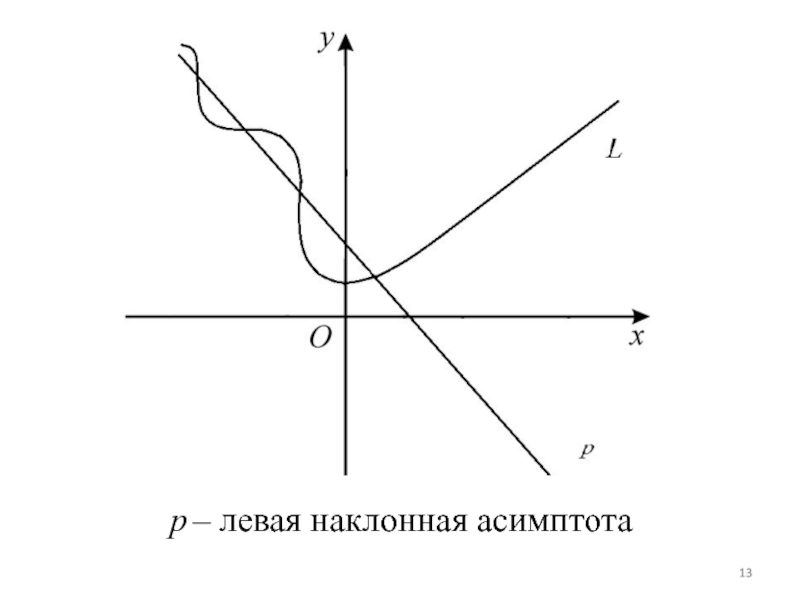
- 13. p – левая наклонная асимптота
- 14. Нас интересуют асимптоты y = f (x).Определение.
- 15. Очевидно, в этом случае x0 является точкой
- 16. Замечание: Легко сделать вывод, что если функция
- 17. Наклонные асимптоты функции бывают правыми и левыми.
- 18. В этом случае, если k = 0,
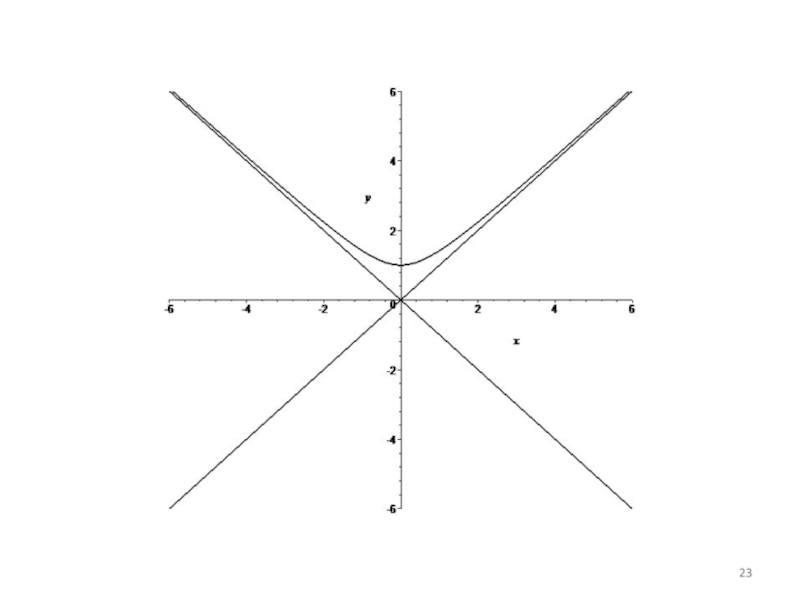
- 19. Пример. Задача. Найти асимптоты функции
- 20. y = x – правая наклонная асимптота
- 21. Найдём левую асимптоту:
- 22. y = – x – левая наклонная асимптота
- 23. Слайд 23
- 24. Как известно, чтобы исследовать функцию на экстремум
- 25. Теорема (достаточное условие экстремума) Если x0 –
- 26. Внутренняя точка x0 области определения функции y
- 27. Определение. Точки минимума и точки максимума обозначаются
- 28. Аналогично о наименьшем и минимальном значениях.Может случиться,
- 29. Теорема (первое достаточное условие экстремума). Если при
- 30. Теорема (об интервалах монотонности). Пусть x1 ,x2
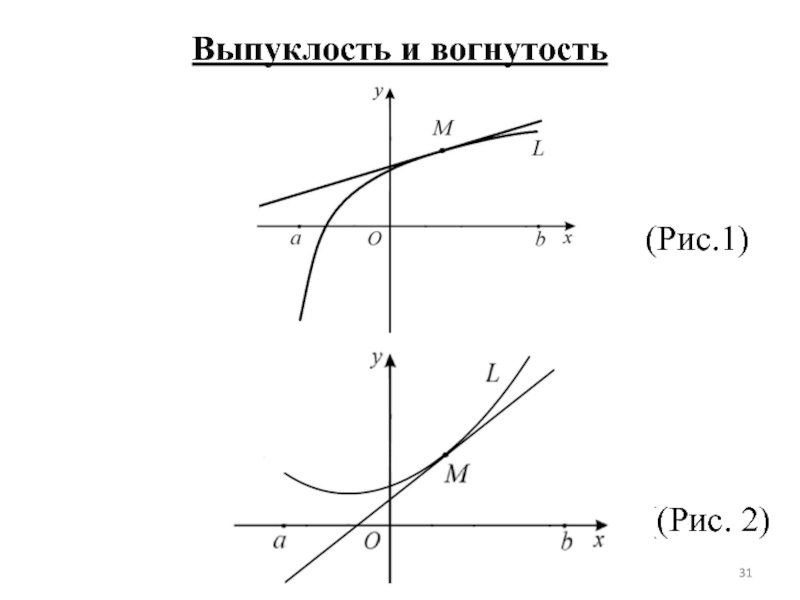
- 31. Выпуклость и вогнутость(Рис.1)((Рис. 2)
- 32. На (рис. 1) изображена выпуклая кривая, на
- 33. Пример. – выпуклая функция– вогнутая функция Справедлива
- 34. Точки перегибаТочка M данной кривой L называется
- 35. Критические точки второго рода называются также точками,
- 36. Теорема (достаточное условие перегиба). Если при прохождении
- 37. Алгоритм исследования функции с помощью второй производной:1)
- 38. 3) Каждую из критических точек второго рода
- 39. Скачать презентанцию
§ 1.Условия постоянства и монотонности функции. Теорема (критерий постоянства). Функция y = f(x) является постоянной на интервале (a ; b) тогда и только тогда, когда её производная тождественно = 0 (
Слайды и текст этой презентации
Слайд 2§ 1.Условия постоянства и монотонности функции.
Теорема (критерий постоянства). Функция
y = f(x) является постоянной на интервале (a ; b)
тогда и только тогда, когда её производная тождественно = 0 ( f (x) = 0) .
Слайд 3Доказательство
« » Это известно из предыдущего.
Пусть x (a ; b) (
f (x) = 0).Требуется показать (!) , что f (x) = const.
Достаточно доказать, что x1, x2 (a ; b) :
(f (x1) = f (x2)). Действительно, пусть x1 < x2
и x1, x2 (a ; b) .
« »
Слайд 4На отрезке [x1 ; x2] функция удовлетворяет всем условиям теоремы
Лагранжа. Действительно, она непрерывна на этом отрезке, поскольку она непрерывна
на интервале (a ; b) .В силу теоремы Лагранжа имеем:
f (x2) – f (x1) = f (С) (x2 –x1) , где С- некоторая точка из С (x1 ; x2) . Но f (С) = 0 , таким образом, f (x2) – f (x1) = 0 f (x2) = f (x1) . Что и требовалось доказать.
![На отрезке [x1 ; x2] функция удовлетворяет всем условиям теоремы Лагранжа. Действительно, она непрерывна на этом отрезке,](/img/thumbs/f479c1b10631df472b57a41ff6ec5670-800x.jpg "Лекция 1 3. Возрастание, убывание функций, необходимые и достаточные условия На отрезке [x1 ; x2] функция удовлетворяет всем условиям теоремы Лагранжа.")
Слайд 5Теорема (достаточные условия монотонности). Пусть x (a ;
b) ( f (x) > 0) f (x) является
возрастающей на интервале (a ; b) .Пусть x (a ; b) ( f (x) < 0) f (x) является убывающей на интервале (a ; b) .
Слайд 6Доказательство
1 часть. f (x) > 0 на интервале (a ;
b) .
(!) x1, x2 (a ; b)
(x1< x2 f (x1) < f (x2)).Возьмём произвольную пару точек x1< x2 (a ; b) . На отрезке (x1,x2) функция удовлетворяет всем условиям теоремы Лагранжа, и значит,что f (x2) – f (x1) = f (С) (x2 –x1). По условию
f (С) > 0, и , стало быть, вся часть положительна, т.е. f (x1) – f (x2) > 0, т.е. f (x1) > f (x2) . Ч.т.д.
Слайд 72 часть. Возьмём произвольную пару точек
x1, x2 (a
; b). На [x1 ; x2] функция удовлетворяет всем условиям
теоремы Лагранжа. И значит,что f (x2) – f (x1) = f (С) (x2 –x1). По условию f (С) < 0 и, стало быть, вся правая часть отрицательна, т.е. f (x2) – f (x1) < 0, т.е.
f (x2) < f (x1). Ч.т.д.
![2 часть. Возьмём произвольную пару точек x1, x2 (a ; b). На [x1 ; x2] функция](/img/thumbs/43078358c3ed4602e98e928b59591259-800x.jpg "Лекция 1 3. Возрастание, убывание функций, необходимые и достаточные условия 2 часть. Возьмём произвольную пару точек x1, x2 (a ;")
Слайд 8§ 2. Полное исследование функций и построение графика .
Задача
исследования функции и построения графика одна из важнейших в математике.
Обычно полное исследование функции производится по следующей схеме:
Слайд 9Алгоритм исследования функции:
1) О.Д.З. D( f ) – область определения
функции.
2) Чётность и периодичность.
3) Исследование на непрерывность. Нахождение асимптот.
4) Исследования,
связанные с f (x) (монотонность, нахождение экстремума, возрастание, убывание).5) Исследования, связанные с f (x) (промежутки выпуклости, вогнутости, точки перегиба).
Слайд 106) Вычисление значений функции в некоторых характерных точках (точек пересечения
графика с осями координат (если имеются), некоторые уточняющие значения).
7)
Используя предыдущее, строим график функции Г ( f ).
Слайд 14Нас интересуют асимптоты y = f (x).
Определение. Прямая x=x0 называется
вертикальной асимптотой функции y = f (x), если хотя бы
один из односторонних пределови
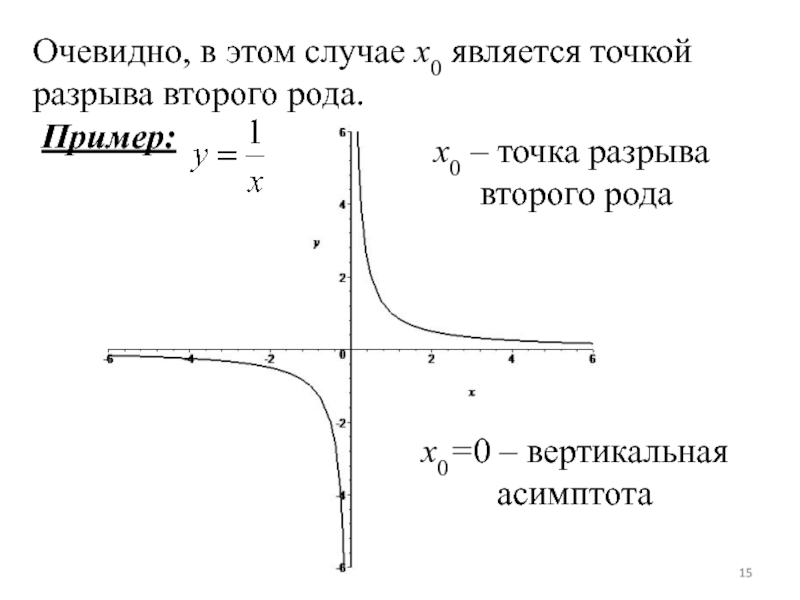
Слайд 15Очевидно, в этом случае x0 является точкой разрыва второго рода.
Пример:
x0 – точка разрыва
второго рода
x0=0 – вертикальная
асимптота
Слайд 16Замечание: Легко сделать вывод, что если функция непрерывна на всей
числовой оси , то у неё нет вертикальных асимптот.
В рассматриваемом
примереy = 0 – горизонтальная асимптота
Общее определение асимптоты (начальное) определение . Прямая p называется асимптотой плоской кривой L, если переменная точка M L неограниченно приближается к прямой p при своём стремлении по кривой к бесконечности.
Слайд 17Наклонные асимптоты функции бывают правыми и левыми. При этом y
= kx + b является правой наклонной асимптотой y =
f (x),если и
(оба предела конечные).
Прямая y = kx + b является левой наклонной асимптотой, если и
Слайд 18В этом случае, если k = 0, асимптота называется горизонтальной.
Таким образом, чтобы найти наклонную асимптоты функции y = f
(x) , нужнонайти соответствующие пределы
и , и если они оказываются
конечными числами, составляется уравнение прямой y = kx + b. В таком случае, если хотя бы один из пределов не является конечным числом, наклонная асимптота не существует.
Слайд 19Пример.
Задача. Найти асимптоты функции
.
D(y) = R;
Вертикальных асимптот нет,
т.к. функция непрерывна на R как композиция двух непрерывных .Найдём правую асимптоту:
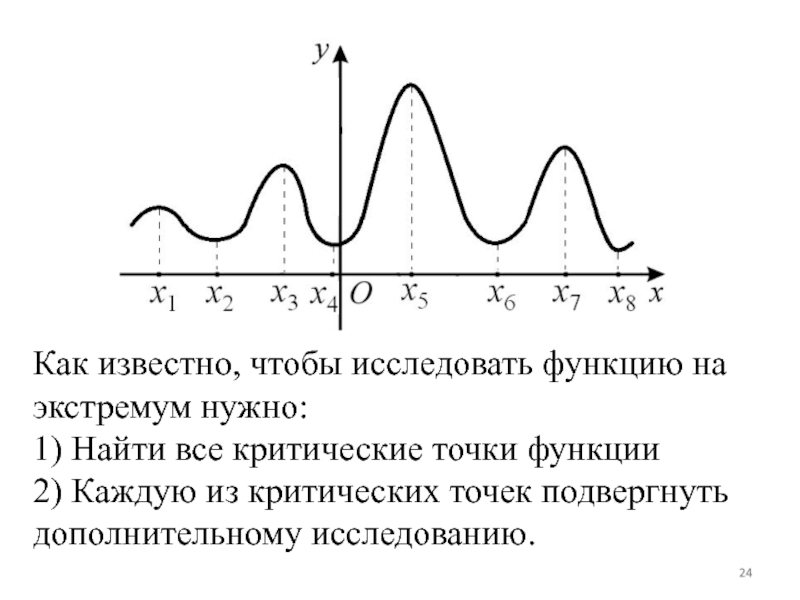
Слайд 24Как известно, чтобы исследовать функцию на экстремум нужно:
1) Найти все
критические точки функции
2) Каждую из критических точек подвергнуть дополнительному исследованию.
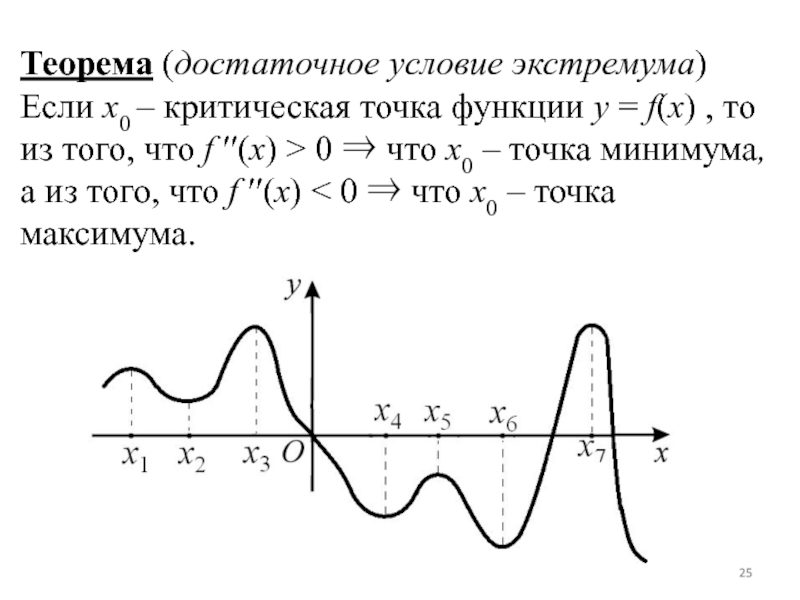
Слайд 25Теорема (достаточное условие экстремума)
Если x0 – критическая точка функции
y = f(x) , то из того, что f (x)
> 0 что x0 – точка минимума, а из того, что f (x) < 0 что x0 – точка максимума.
Слайд 26Внутренняя точка x0 области определения функции y = f (x)
называется точкой максимума этой функции, если существует такая (быть может
достаточно малая) окрестность Ơ x0 , чтоx Ơ x0 (x ≠ x0 ) (f (x0) > f (x)).
f (x0) называется максимальным значением функции, таким образом, максимальное значение функции – наибольшее значение в локальном смысле.
Аналогично определение точек минимума, лишь неравенство будет выглядеть так: f (x0) < f (x), т.е. минимальное значение это есть наименьшее значение в локальном смысле.
Слайд 27Определение. Точки минимума и точки максимума обозначаются под общим названием
точки экстремума.
Замечание 1: Очень важным является то, что точка экстремума
является внутренней для D( f ).Замечание 2: Максимальные и минимальные значения следует отличать от наибольшего и наименьшего значений функции. Максимальных и минимальных значений функции может быть очень много. Наибольшее и наименьшее проставлено каждое единственным образом.
Наибольшее значение является наибольшим в глобальном смысле, а максимальное – в локальном.
Слайд 28Аналогично о наименьшем и минимальном значениях.
Может случиться, что некоторое максимальное
значение является меньше минимального.
Теорема (необходимость условия экстремума)
Пусть x0 –
точка экстремума функции, тогда она является критической точкой данной функции (это легко вытекает из теоремы Ферма). Таким образом, точки экстремума нужно искать среди критических точек. 
Слайд 29Теорема (первое достаточное условие экстремума). Если при прохождении через критическую
точку производная меняет знак, то данная точка является точкой экстремума,
а именно: точкой максимума, если знак производной меняется с «+» на «–» и точкой минимума, и точкой минимума, если знак меняется с «–» на «+».Это легко вытекает из достаточного условия монотонности и теоремы Лагранжа.
Слайд 30Теорема (об интервалах монотонности). Пусть
x1 ,x2 , …xn –
все критические точки функции
y = f (x), тогда на
каждом из интервалов (–∞ ; x1); (x1 ; x2 ) …… (xn-1 ; xn ) ; (xn ; +∞) производная сохраняет знак (свой для каждого интервала).Считаем, что D( f )=R.
Без доказательства
Слайд 32На (рис. 1) изображена выпуклая кривая, на (рис. 2) –вогнутая
кривая.
Определение. Гладкая кривая L называется выпуклой на интервале (a ;
b) , если она находится под любой своей касательной(L: y = f (x)) и называется вогнутой, если она находится над любой своей касательной в пределах данного интервала.
Определение. Функция y = f (x) называется выпуклой на интервале (a,b) , если её график является выпуклой кривой. И функция y = f (x) называется вогнутой на (a ; b) , если её график является вогнутой кривой.
Слайд 33Пример.
– выпуклая функция
– вогнутая функция
Справедлива Th.
Теорема (достаточное условие
выпуклости – вогнутости). Если на (a ; b) f (x)
< 0 функция выпуклая, если на (a ; b) f (x) > 0 функция вогнутая на интервале (a ; b) .Определение. Внутренняя точка x0 D( f ) называется критической точкой второго рода, если вторая производная f (x) не существует, либо f (x) = 0.
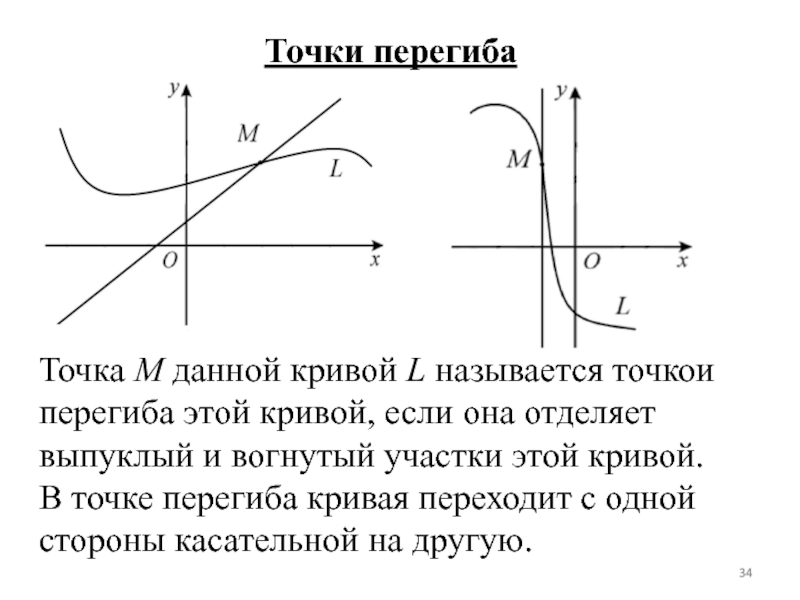
Слайд 34Точки перегиба
Точка M данной кривой L называется точкой перегиба этой
кривой, если она отделяет выпуклый и вогнутый участки этой кривой.
В
точке перегиба кривая переходит с одной стороны касательной на другую.
Слайд 35Критические точки второго рода называются
также точками, подозрительными на перегиб.
Определение.
Внутренняя точка x0 D( f ) , называется точкой
перегиба функции y = f (x), если точкаM (x0; f (x0)) является точкой перегиба её графика.
Теорема (необходимое условие перегиба). Пусть x0 – точка перегиба функции y = f (x), тогда она является критической точкой второго рода этой функции , т.е. точки перегиба искать среди критических точек второго рода.
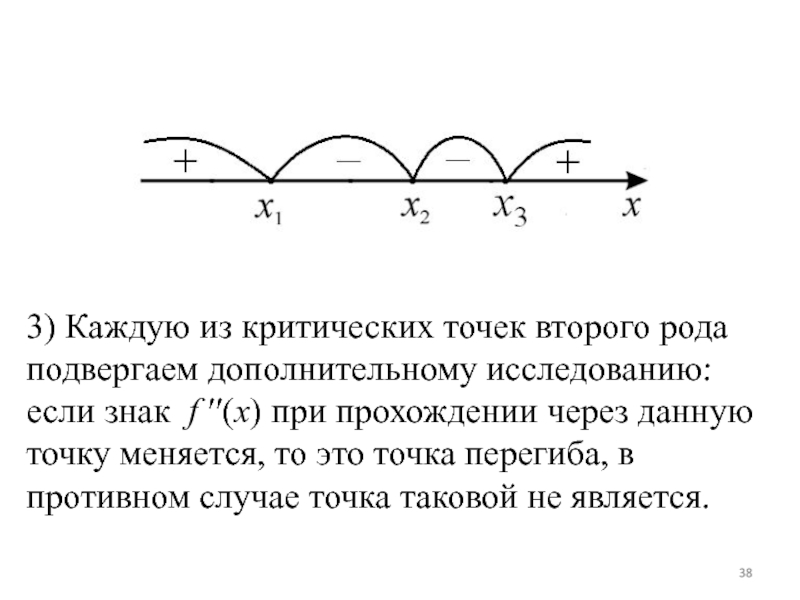
Слайд 36Теорема (достаточное условие перегиба). Если при прохождении через критическую точку
второго рода знак второй производной меняется, то эта точка является
точкой перегиба.Теорема (об интервалах выпуклости и вогнутости). Пусть x1 , x2 ,…xn – все критические точки второго рода функции
y = f (x), D( f )=R, тогда на каждом из интервалов (–∞; x1) ; (x1 ; x2 ) …… (xn-1 ; xn ) ; (xn ;+∞) вторая производная сохраняет знак.
Слайд 37Алгоритм исследования функции с помощью второй производной:
1) Находим все критические
точки второго рода (находим f (x), приравниваем к «0» и
смотрим, где она не существует). Они разбивают D( f ) на интервалы.2) На каждом из полученных интервалов вычисляем знак f (x).
Слайд 383) Каждую из критических точек второго рода подвергаем дополнительному исследованию:
если знак f (x) при прохождении через данную точку меняется,
то это точка перегиба, в противном случае точка таковой не является.
