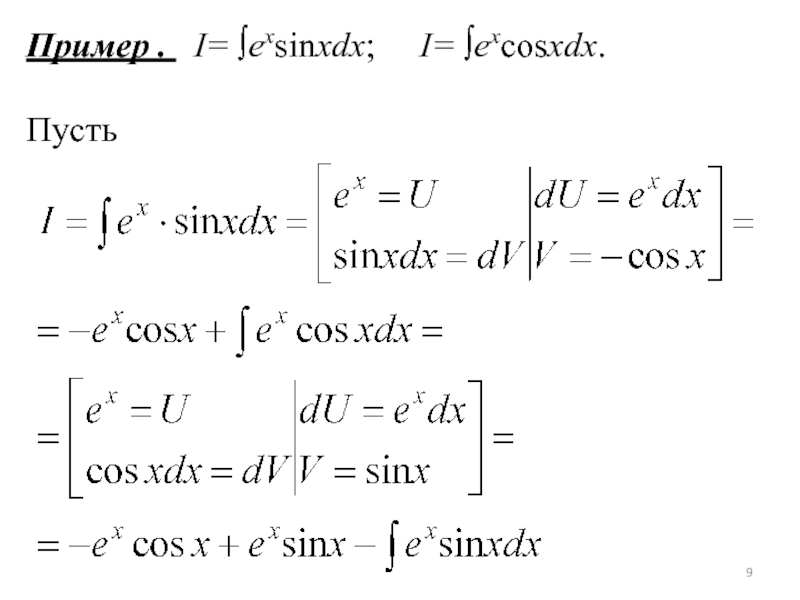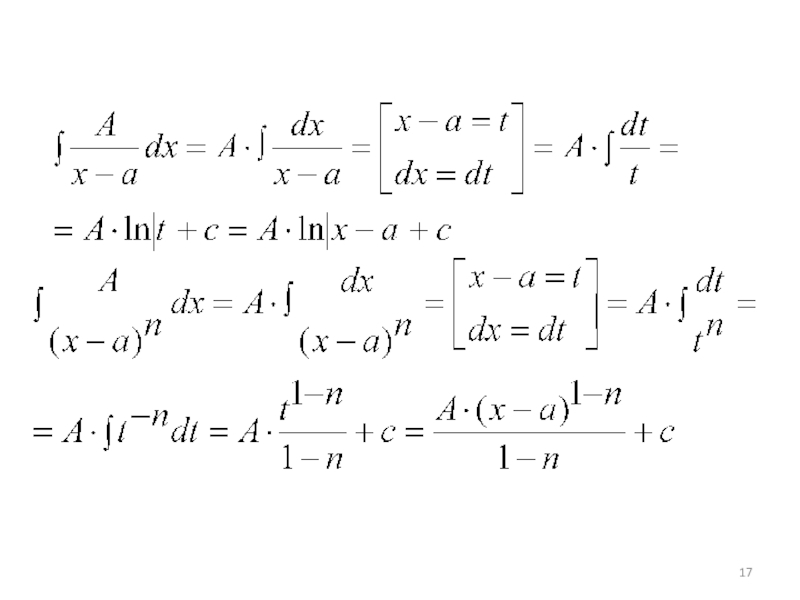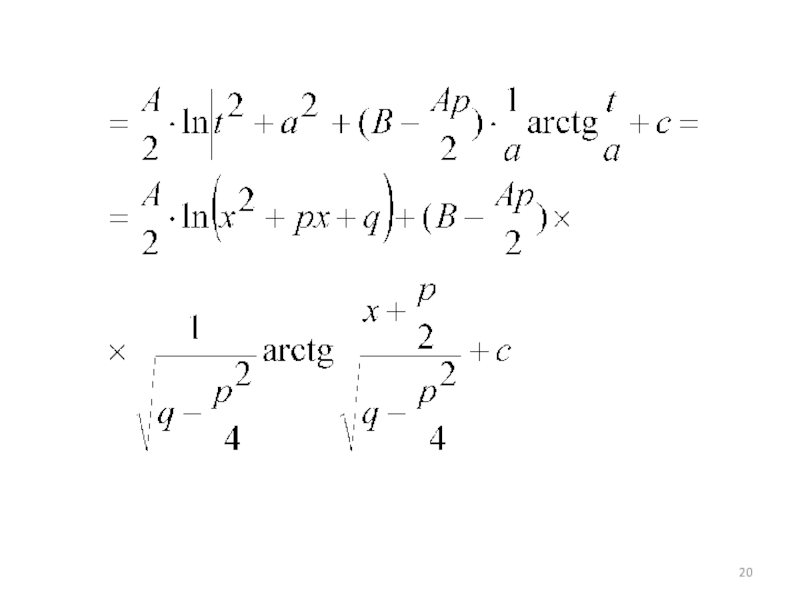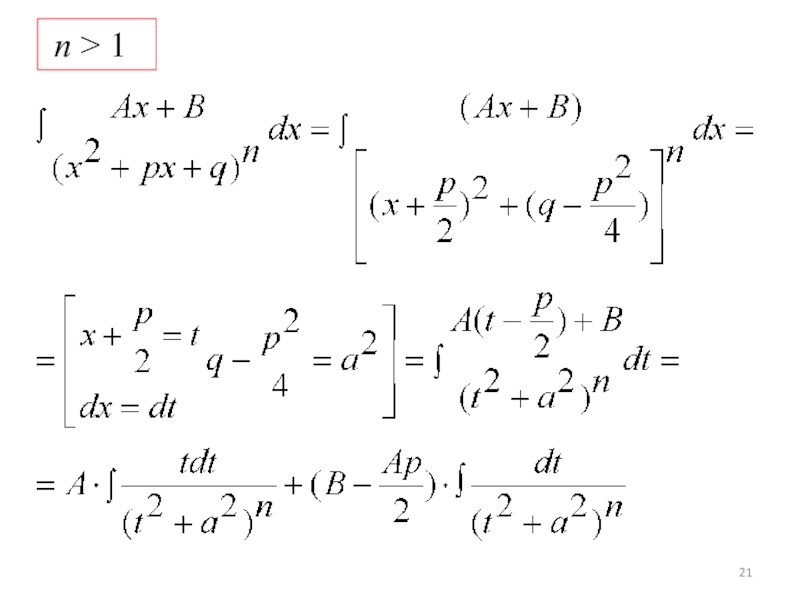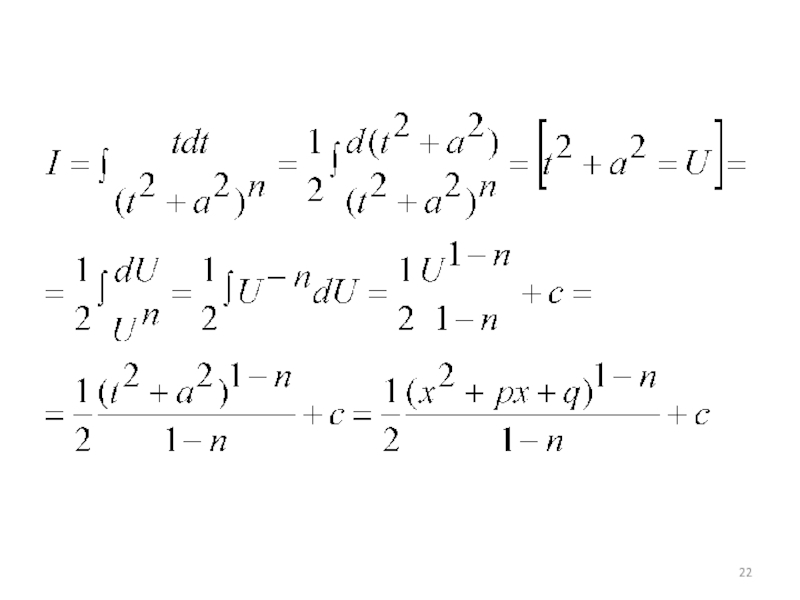Лекция 1 5. Основные методы интегрирования, интегрирование рациональных

и тригонометрических функций.

метод после метода подстановки.
Формула интегрирования по частям является обращением формулы

дифференциала произведения.
Пусть U=U(x) и V=V(x) – некоторые функции.
d(U·V)=dU·V+U·dV→UdV=d(U·V) – VdU.

интеграла от ∫UdV к вычислению интеграла ∫VdU , что бывает

намного проще.

∫UdV=U·V – ∫VdU

в том, как лучше разбить подынтегральное выражение так, чтобы ∫V·dU

был простым для вычисления.

Пример 2.

мы разбиваем подынтегральное выражение ∫UdV на U и dV, то

dx содержится в dV.

по частям.
И вообще: xnsinxdx; ∫ xncosxdx; ∫ xnexdx берутся n

раз по частям. (Каждое применение метода по частям понижает степень x на единицу.)
Случается так, что повторное применение к интегралу метода интегрирования по частям приводит интеграл к самому себе. В этом случае мы имеем либо ничего не дающее тождество, т.е. интегрирование было проведено нерационально, либо получаем линейное уравнение относительно этого интеграла, и откуда его находим.

= ex (sinx – cosx);
I=(1/2) ex (sinx – cosx) +

c
По значимости этот метод (после метода подстановки) занимает 2 – е место, однако есть интегралы, которые могут быть вычислены только этим методом:
∫xneaxdx xn = U
∫ xnsinaxdx
∫ xncosaxdx

∫xnlnmxdx lnx = U
∫ xnarctgxdx
∫ xnarcsinxdx

n ϵ N).

Pn(x)=a0+a1x+…+anxn
∫Pn(x)=a0∫dx+a1∫xdx+…+an∫xndx =a0x+a1(x2/2)+
+an(xn+1/n+1)+c.

∫ cosmxdx;
а). m=2k+1 (нечётная)
∫ cosmxdx =

∫ cos2k+1xdx = ∫ cos2kx·cosxdx =
= ∫ (cos2x)k·dsinx = ∫ (1 – sin2x)kdsinx = [sinx = t] =
= ∫ (1 – t2)kdt – получим интеграл от многочлена, который легко вычисляется.

∫ (cos2x)kdx =
= ∫((1+cos2x)/2)kdx = (1/2k)∫(1+cos2x)kdx
Под знаком ∫ мы

получили так называемый тригонометрический многочлен, переменной в котором является cos2x, причём многочлен в степени k , т.е. в два раза ниже, чем была в начале. Далее интегрируя этот тригонометрический многочлен:
∫(a0+a1cos2x+a2cos22x+…+akcosk2x)dx
Степени cos здесь чётные и нечётные, где нечётные – доводим до конца, где чётные – вновь понижаем в два раза, как это было в начале.

табличные интегралы.
Пример :

1). ∫ cos3xdx = ∫ cos2x·cosxdx =

∫ cos2x·dsinx =
= ∫ (1-sin2x)dsinx = [sinx = t] = ∫ (1 – t2)dt =
= t – (t3/3)+c = sinx – (1/3)sin3x+c.

2). ∫ cos2xdx = ∫((1+cos2x)/2)dx
∫cos4xdx = ∫(cos2x)2dx = ∫((1+cos2x)2/2)dx =
= (1/4)∫(1+2cos2x+cos22x)dx – нет проблем.
Относительно ∫ sinmxdx рассуждения аналогичны, а именно:

sinmxdx = ∫ sin2k+1xdx = ∫ sin2kx·sinxdx =
= – ∫

(1-cos2x)kdcosx = [cosx = t]= ∫ (1 – t2)kdt

б). m = 2k. Здесь:
∫ sinmxdx = ∫ sin2kxdx = ∫((1 – cos2x)/2)kdx =
= (1/2k) ∫(1 – cos2x)kdx

– рациональная

функция, где

Pn(x), Qm(x) многочлены соответствующих степеней n и m , n,m ϵ N. По другому такие функции называются рациональными дробями. При этом рациональная дробь называется правильной, если степень числителя строго меньше степени знаменателя n < m , и называется неправильной в противном случае
n ≥ m , т.е. степень числителя больше или равна степени знаменателя.

,

, n > 1 (1)


, , n > 1, D < 0, т.е. (2)
p2 – 4q < 0

Дроби вида (1) называются простыми рациональными дробями первого рода, и вида (2) – второго рода

что q – (p2/4) > 0
(4q – p2)/4) > 0

, т.к. p2 – 4q < 0
Это даёт нам основание ввести обозначение
q – (p2/4) = a2

представить в виде суммы простых рациональных дробей (см. учебники).
Пример:

эту дробь в виде суммы простых рациональных дробей.
Проинтегрировать полностью полученную

сумму.

Пусть f(x)-неправильная рациональная дробь

, n ≥ m

деления будет либо многочлен (если нацело), либо сумма многочлена и

правильной рациональной дроби.
Рациональная функция всегда интегрируема.

«О разложении рациональной дроби в сумму простых»