Слайд 1Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Лекция 1. Сфера
и границы
применения экономико-математического моделирования
Содержание лекции:
Понятие экономико-математического моделирования
Принцип гомоморфизма – научная
основа моделирования
Сфера применения метода моделирования
Классификация экономико-математических моделей
Этапы экономико-математического моделирования
Слайд 2Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Литература
Экономико-математические методы и
прикладные модели: Учеб. пособие для вузов / Под ред. В.В.
Федосеева. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — глава 1.
Резниченко С.С., Подольский М.П., Ашихмин А.А. Экономико-математические методы и моделирование в планировании и управлении горным производством, М., «Недра» 1991 г. 429с.
Слайд 3Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.1. Понятие экономико-математического
моделирования
Модель – это упрощённое подобие реального объекта, используемое для его
исследования
Модель – это система, гомоморфная исследуемой системе (называемой объектом моделирования) и используемая для суждения об её свойствах и поведении.
Моделирование – непрерывный процесс совершенствования модели, в котором знания о реальном объекте извлекаются из выявления несоответствий между моделью и объектом, их осмысления и устранения.
Математическое моделирование – метод исследования реальных объектов при помощи постановки экспериментов на их математических моделях.
Экономико-математическое моделирование (по В.С.Немчинову) – это концентрированное выражение наиболее существенных взаимосвязей и закономерностей поведения управляемой системы в математической форме.
Слайд 4Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Основные понятия и
определения.
2. Математическая модель и ее свойства.
Определение. Математическая модель – это
некоторый математический образ исследуемой экономической системы, который адекватно отражает структуру переменных системы, их свойства и взаимосвязи.
Модель может быть представлена в виде набора графиков, таблиц или системы математических уравнений и неравенств, с помощью которых можно однозначно определить значения одних переменных по известным значениям других переменных.
Слайд 5Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Метод математического моделирования
в экономике
Определение. ЭММ представляет собой одну из фундаментальных математических дисциплин,
стремящихся приоткрыть занавес над устройством внутренних механизмов сложных экономических систем
Цель ЭММ – количественная оценка экономических процессов, протекающих в рамках исследуемой экономической системы
Экономическая система – любой хозяйствующий объект вне зависимости от формы собственности
Слайд 6Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
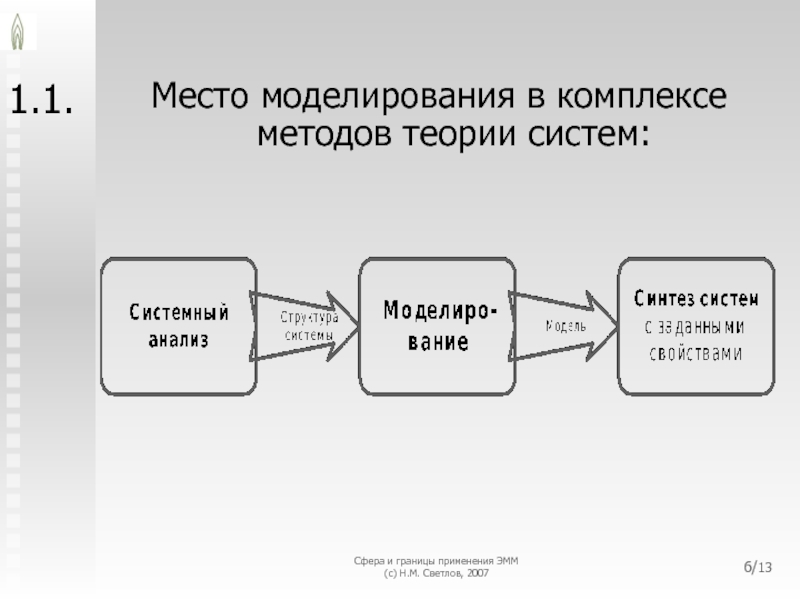
1.1.
Место моделирования
в комплексе методов теории систем:
Слайд 7Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.2. Принцип гомоморфизма
– научная основа моделирования
Слайд 8Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.2.
Гомоморфизм – это
логико-математическое понятие, означающее одностороннее отношение подобия между двумя системами.
Систему называют
гомоморфной другой системе, если первая обладает некоторыми, но не всеми, свойствами или законами поведения другой.
Слайд 9Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Основные понятия и
определения
3. Основные свойства модели
Простота. Полнота. Адекватность.
Простота. Проста в понимании. Простота
математического аппарата. Не отягощена лишними переменными, которые слабо влияют на развитие экономической системы (Все гениальное – просто)
Полнота. Включены все факторы, влияющие на достижение цели. Учтены все условия, которые ограничивают развитие системы. Имеется возможность получить ответ на все вопросы, поставленные в задаче.
Адекватность. Возможность достижения цели с приемлемой точностью.
Слайд 10Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Основные понятия и
определения
4. Основные свойства модели
Модель – это компромисс между полнотой и
простотой, точностью и размерностью, эффективностью и затратами на ее реализацию.
Модель – объект заместитель объекта оригинала, который в определенных условиях может заменить оригинал.
Модель – результат идеализации и рафинирования реального экономического объекта.
Слайд 11Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.3. Сфера применения
метода моделирования
Объект недоступен для непосредственного исследования (причины радиоизлучения квазаров, процессы
формирования кимберлитовых трубок)
Уникальный или дорогостоящий объект разрушится вследствие исследования (предельная нагрузка на железнодорожный мост)
Исследование на реальном объекте дорого, трудоёмко или опасно (влияние биологических средств борьбы с вредителями сельскохозяйственных культур)
Исследование на реальном объекте займёт неприемлемо долгое время (процесс формирования каменноугольных залежей)
Реальный объект не существует: изучается возможность и целесообразность его создания (скоростная железнодорожная магистраль Москва – Васюки)
Слайд 12Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.3.
Причины, ограничивающие применение
моделирования
Никогда нельзя быть уверенным в адекватности модели.
Не существует строгого метода
доказательства существования отношения гомоморфизма. Обычно гомоморфизм обосновывается индуктивно, что чревато ошибками.
Объект моделирования может быть подвержен изменениям.
Модель, успешно работавшая в прошлом, не обязательно окажется полезной в настоящем.
Границы применимости модели, как правило, неизвестны.
Результаты одних модельных экспериментов могут быть полезными, других – нет.
Разработка и исследование модели могут оказаться намного дороже, чем предполагалось.
Слайд 13Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.4. Классификация экономико-математических
моделей
По целевому назначению
Теоретические
Прикладные
По степени агрегирования
Макро-экономические
Микро-экономические
Нано-экономические
Слайд 14Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.4. Классификация экономико-математических
моделей
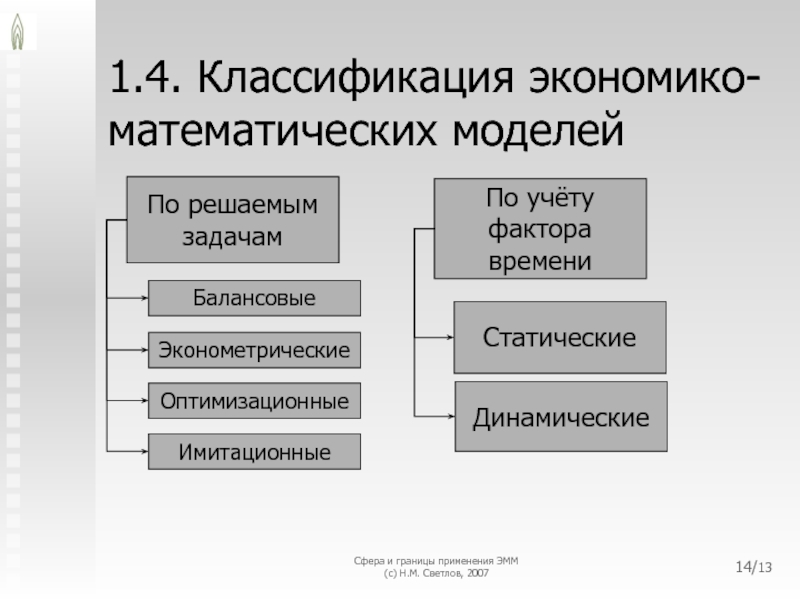
По решаемым задачам
Балансовые
По учёту фактора времени
Статические
Динамические
Эконометрические
Оптимизационные
Имитационные
Слайд 15Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.4. Классификация экономико-математических
моделей
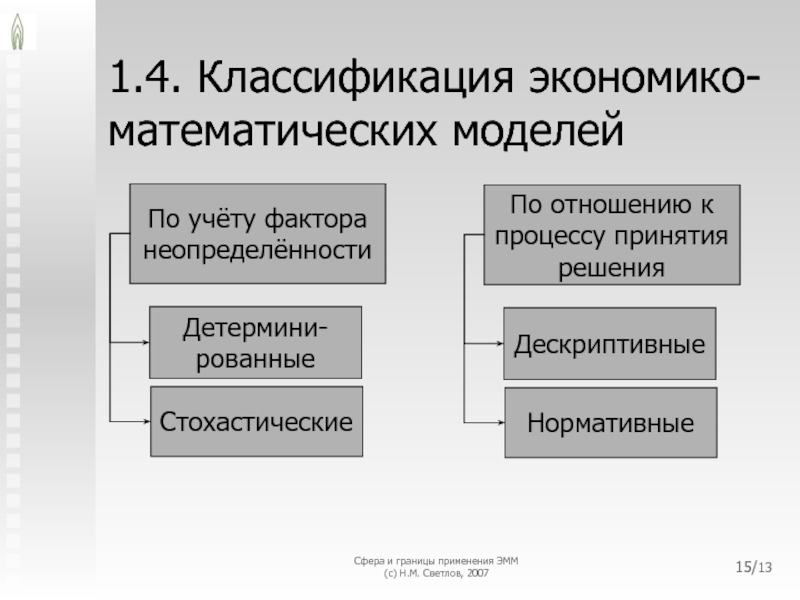
По отношению к процессу принятия решения
Дескриптивные
Нормативные
По учёту фактора неопределённости
Детермини-рованные
Стохастические
Слайд 16Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.4.
Методы теории систем
Системный
анализ
Синтетический метод
Методы математической статистики
Дисперсионный анализ
Корреляционный анализ
Регрессионный анализ
Факторный анализ
Кластерный анализ
Теория индексов
Методы
исследования операций
Математическое программирование
линейное
сепарабельное
целочисленное
дробно-линейное
нелинейное
динамическое
параметрическое
стохастическое
Методы теории игр
Методы теории расписаний
Методы теории массового обслуживания
Управление запасами
Классификация математических методов, используемых для разработки и исследования ЭММ
Слайд 17Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
1.5. Этапы экономико-математического
моделирования
Постановка экономической проблемы
Построение математической модели
Математический анализ модели
Эмпирическая спецификация модели
Подготовка исходных
данных
Численное решение модели
отыскание оптимального решения
параметрическая идентификация (оценивание)
вычислительный эксперимент
Анализ полученных результатов
Подготовка и принятие управленческих решений
Слайд 18Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Основные понятия и
определения
7. Основные математические модели и задачи
Задачи математического программирования
Модели конфликтных ситуаций
в экономике
Модели сетевого планирования и управления
Модели системы массового обслуживания
Модели сферы потребления
Модели сферы производства
Модели общего экономического равновесия
Общие модели развития экономики
Любая задача экономики сводится к задаче принятия решения или задаче управления
Слайд 19Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Основные понятия и
определения
Принятие решения является повседневной задачей человека
Решения приходится принимать в различных
ситуациях:
- как с наибольшей пользой потратить имеющиеся средства
- как наиболее эффективно организовать производство того или иного продукта
- как рационально спланировать производственный цикл
-какую стратегию поведения выбрать, чтобы остаться «на плаву» в условиях конкуренции
Во всех случаях речь идет о выборе наилучшего (оптимального) решения.
В основе всех экономических проблем лежит задача оптимизации
Именно эти задачи занимают центральное место в экономико-математическом моделировании.
Слайд 20Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Основные понятия и
определения.
8. Структура экономической задачи.
Факторы
х1
х2
х3
Ограничения
Ограничения
Внешняя среда
Результат
Y
Экономическая Система
Слайд 21Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
Леонид Витальевич
Канторович родился 19 января 1912г. в Санкт-Петербурге в семье врача.
В 18 лет он закончил математический факультет Ленинградского университета (1930) и уже через четыре года получил звание профессора. Л.В.Канторович является одним из основателей отечественных школ функционального анализа. вычислительной математики, языков программирования.
С 1938г. интересы Л.В.Канторовича были неразрывно связаны с экономическими исследованиями и решением народнохозяйственных проблем.
Крупнейшим его открытием является введение в математическую и экономическую науки понятия "линейное программирование" (1939). Линейное программирование является универсальной математической моделью оптимального функционирования экономических систем. Основная заслуга Л.В.Канторовича заключается в разработке единого подхода к широкому кругу экономических задач о наилучшем использовании ресурсов на базе линейного программирования.
Слайд 22Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
Василий Леонтьев
Родился
в Санкт-Петербурге в 1906 г. В 1925 г. окончил Ленинградский
университет. В 1925-28 гг. учился в Берлинском университете. В 1931 г. Леонтьев переезжает в США, где работает в течение 44 лет в Гарвардском университете
Особую известность Леонтьев получил как автор метода экономического анализа "затраты-выпуск" (Input-output). Этот метод использован Леонтьевым при построении моделей межотраслевых балансов экономики США
В круг его интересов входят математические методы и модели в экономике, международная торговля, анализ теорий Маркса и Кейнса, построение индексов, механизм спроса и предложения. экономические циклы и многое другое.
Слайд 23Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
Джон Мейнард
Кейнс (1883 - 1946)
Дж. М. Кейнс рассматривается большинством экономистов и
политических деятелей как наиболее значительный экономист-теоретик XX века.
Его научная разносторонность выявилась в том, что в молодости он достиг значительных успехов в математике и написал диссертацию по теории вероятности, а в более зрелом возрасте смог достичь выдающихся успехов и как экономист-теоретик,
Кейнс открыл целое направление исследований, в рамках которого сегодня работает чуть ли не половина всех экономистов мира. Речь идет о направлении, связанном с изучением функционирования экономики, взятой в целом, - о макроэкономике.
Слайд 24Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
Джон фон
Не́йман (нем. John von Neumann, или Янош Лайош Не́йман
(28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как праотец современной архитектуры компьютеров (так называемая архитектура фон Неймана), применением теории операторов, а также как участник Манхэттенского проекта и как создатель теории игр и концепции клеточных автоматов.
Слайд 25Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
Роберт Мертон
Солоу; род. 23 августа 1924, Нью-Йорк) — американский экономист.
Лауреат Нобелевской премии
1987 г. «за фундаментальные исследования в области теории экономического роста».
Ветеран Второй мировой войны. Профессор Массачусетского технологического института.
Президент Международной экономической ассоциации (1999—2002). Президент Эконометрического общества (1964). Президент Американской экономической ассоциации в 1979 г.
Награждён медалями Дж. Б. Кларка (1961) и В. Леонтьева "За достижения в экономике" (2006).
Лауреат премий Джона Коммонса (1971), Ф. Сейдмана (1983) и А. Смита (1985).
Слайд 26Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
Гарри МАРКОВИЦ
(род. в 1927 г.)
Особый интерес с самого начала вызывала у
него "экономика неопределенности", в особенности, идеи Дж. фон Неймана, О. Моргенштерна, Дж. Маршака относительно функции полезности.
Для своей докторской диссертации М. избрал исследование возможности применения математических методов к рынку ценных бумаг. В процессе работы над темой у него сложилась в основном концепция портфельных инвестиций, за которую он впоследствии получит Нобелевскую премию
Главная заслуга Г.Марковца заключается в разработке точно сформулированной, пригодной для применения, теории для выбора портфельных инвестиций в условиях неопределенности, которая послужила основанием для последующих разработок в области экономики финансов.
Слайд 27Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
ПЕТТИ, УИЛЬЯМ
(Petty, William) (1623–1687), английский экономист и статистик. Родился 26 мая
1623 в семье небогатого ремесленника-суконщика в Ромси (графство Хэмпшир).
Петти оставил заметный след в истории экономической науки, хотя единой точки зрения на его научный вклад до сих пор не существует. Основные труды Петти – Трактат о налогах и сборах (A Treatise of Taxes and Contributions, 1662); Слово мудрым (Verbum Sapienti, 1665); Политический обзор, или анатомия Ирландии (Political Survey or Anatomy of Ireland, 1672); Разное о деньгах (Quantulumcunque Concerning Money, 1682); и Эссе о политической арифметике (Essays in Political Arithmetick, 1683
Слайд 28Сфера и границы применения ЭММ
(с) Н.М. Светлов, 2007
/13
Известные ученые-экономисты
Кене Франсуа,
(4 июня 1694 -16 декабря 1774), французский экономист, основоположник школы
физиократов. К экономическим исследованиям Кёне приступил уже на склоне лет. Первые его статьи по этому предмету были напечатаны в «Энциклопедии» Дидро, в 1756 г. В 1758 г. он напечатал «Экономическую таблицу»