Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 1 ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Содержание
- 1. Лекция 1 ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- 2. Любая точная наука изучает не сами явления,
- 3. Задачи, исход которых нельзя предсказать с
- 4. Статистические закономерности исследуются методами специальных математических дисциплин
- 5. Элементы комбинаторики Упорядоченным называется множество, в котором указан
- 6. Размещения из n элементов по k элементов Пусть
- 7. Для числа размещений справедлива формула:
- 8. Перестановки из n элементов Размещение из n элементов
- 9. Сочетания из n элементов по k элементов Пусть
- 10. Для числа сочетаний справедлива формула
- 11. Пример Для проведения экзамена создается комиссия из двух
- 12. Пример На втором курсе изучают 10 различных предметов.
- 13. События и вероятность Эксперимент, испытание, опыт, процесс —
- 14. Среди событий отличают достоверное и невозможное события.
- 15. Примеры событий: выпадение орла при бросании монеты,
- 16. Любое событие А из пространства можно составить
- 17. Событие называется случайным, если оно может произойти,
- 18. События A, B, C, … называются попарно-несовместными,
- 19. Несколько событий в данном опыте называются равновозможными,
- 20. Действия над событиями Суммой событий A и B
- 21. Разностью событий A и B называется
- 22. Понятие вероятности Под вероятностью события понимается некоторая числовая
- 23. Статистическое определение вероятности Пусть при проведении n
- 24. Классическое определение вероятности Классической схемой, или схемой случаев,
- 25. Классической вероятностью события А называется отношение числа
- 26. Свойства вероятностей 1. Вероятность невозможного события равна нулю,
- 27. Пример В коробке имеются 10 шаров, которые различаются
- 28. Пример В коробке 5 синих, 4 красных и
- 29. Геометрическое определение вероятности Геометрическое определение вероятности применяется в
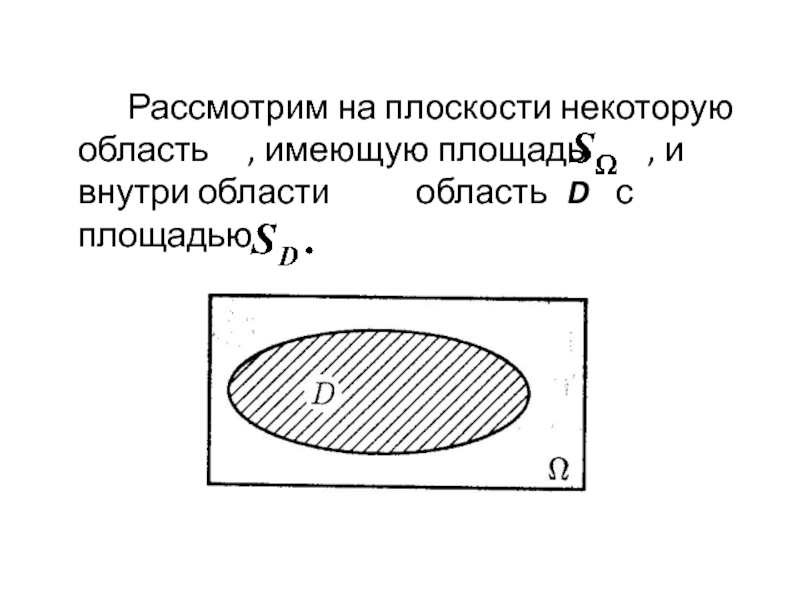
- 30. Рассмотрим на плоскости некоторую область , имеющую
- 31. В области случайно выбирается точка X.
- 32. Геометрической вероятностью события A называется отношение площади
- 33. В первом случаеВо втором:где — длина, а V — объем соответствующей области.
- 34. Геометрическая вероятность обладает всеми свойствами, присущими классическому
- 35. Пример После бури на участке между 40-м и
- 36. Скачать презентанцию
Любая точная наука изучает не сами явления, протекающие в природе, в обществе, а их математические модели, т. е. описание явлений при помощи набора строго определенных символов и операций над ними.
Слайды и текст этой презентации
Слайд 3 Задачи, исход которых нельзя предсказать с полной уверенностью, требуют
изучения не только основных, главных закономерностей, определяющих явление в общих
чертах, но и случайных, второстепенных факторов.Выявленные в таких задачах (опытах) закономерности называются статисти-ческими (или вероятностными).
Слайд 4 Статистические закономерности исследуются методами специальных математических дисциплин — теории вероятностей
и математической статистики.
Теория вероятностей — математическая наука, изучающая закономерности, присущие
массовым случайным явлениям.Предметом теории вероятностей являются математические модели случайных явлений.
Слайд 5Элементы комбинаторики
Упорядоченным называется множество, в котором указан порядок следования элементов.
Так, например, множества (a, b, c) и (a, c, b)
есть различные упорядоченные множества.Слайд 6Размещения из n элементов по k элементов
Пусть некоторое множество А
содержит n элементов. Каждое его упорядоченное подмножество, состоящее из k
элементов, называется размещением из n элементов по k элементов.Через обозначают число всех размещений из n элементов по k (читается: «А из n по k»).
Слайд 8Перестановки из n элементов
Размещение из n элементов по n называется
перестановкой из n элементов.
Количество всех таких перестановок обозначается .
Из предыдущей формулы получимСлайд 9Сочетания из n элементов по k элементов
Пусть задано множество, состоящее
из n элементов.
Сочетанием из n элементов по k элементов называется
каждое неупорядоченное подмножество, содержащее k элементов.Число всех сочетаний из n элементов по k элементов обозначается
Слайд 11Пример
Для проведения экзамена создается комиссия из двух преподавателей. Сколько различных
комиссий можно составить из 5 преподавателей?
Решение.
Слайд 12Пример
На втором курсе изучают 10 различных предметов. Сколькими способами можно
составить расписание занятий на понедельник, если в этот день должно
быть 4 различных предмета?Решение.
Слайд 13События и вероятность
Эксперимент, испытание, опыт, процесс — это возникновение или
преднамеренное создание определенного комплекса условий результатом которого является тот
или иной исход.Событием называется исход испытания. События обозначаются большими латинскими буквами А, В, С, ....
Слайд 14 Среди событий отличают достоверное и невозможное события.
Достоверное событие —
это такое событие, которое всегда происходит при выполнении данного комплекса
условий. Оно обозначается .Невозможное событие — это такое событие, которое не может произойти при выполнении определенного комплекса условий.
Обозначается
Слайд 15 Примеры событий: выпадение орла при бросании монеты, выигрыш по облигации,
увеличение курса доллара в следующем месяце, появление заявки на телефонной
станции и т.д.Элементарными называются те из событий, которые нельзя разложить на составляющие их события. Элементарные события будем обозначать буквой
Обозначим - пространство элементарных событий.
Слайд 16 Любое событие А из пространства
можно составить из элементарных событий.
Пример
В
опыте с бросанием игральной кости (кубика) элементарными событиями являются выпадения
чисел 1, 2, 3, 4, 5, 6.В этом же опыте событиями являются выпадения четного или нечетного числа.
Слайд 17 Событие называется случайным, если оно может произойти, а может не
произойти в данном опыте.
Два события называются несовместными, если появление одного
из них исключает появление другого в одном и том же опыте.В противном случае события называются совместными.
Слайд 18
События A, B, C, … называются попарно-несовместными, если любые два
из них несовместны.
Несколько событий образуют полную группу, если они попарно
несовместны и в результате каждого опыта происходит одно и только одно из них.Слайд 19 Несколько событий в данном опыте называются равновозможными, если ни одно
из них не является объективно более возможным, чем другие, т.
е. все события имеют равные «шансы».Пример
Подбрасываем монету.
Слайд 20Действия над событиями
Суммой событий A и B называется событие C=A+B,
состоящее в наступлении хотя бы одного из них (т. е.
или A, или B, или A и B вместе).Произведением событий A и B называется событие C=AB состоящее в совместном наступлении этих событий (т. е. A и B одновременно).
Слайд 21 Разностью событий A и B называется событие C=A-B происходящее
тогда и только тогда, когда происходит событие А, но не
происходит событие В.Противоположным событию A называется событие которое происходит тогда и только тогда, когда не происходит событие A.
Равенство событий А = В означает, что А В и В А, т.е. они состоят из одних и тех же элементарных событий.
Слайд 22Понятие вероятности
Под вероятностью события понимается некоторая числовая характеристика возможности наступления
этого события. Существует несколько определений понятия вероятности.
Слайд 23Статистическое определение вероятности
Пусть при проведении n испытаний некоторое событие
А появилось т раз. Многочисленные эксперименты такого рода показывают, что
при больших n отношение m/n называемое частотой события А, остается примерно постоянным.При статистическом определении вероятностью события А называется постоянная величина, вокруг которой колеблются значения частот при неограниченном возрастании числа n.
Слайд 24Классическое определение вероятности
Классической схемой, или схемой случаев, называется испытание, при
котором число элементарных исходов конечно и все из них равновозможны.
Элементарное
событие (исход) называется благоприятствующим событию А, если его появление влечет наступление события А (т.е. входит в число элементов, составляющих А).Слайд 25 Классической вероятностью события А называется отношение числа т элементарных событий,
благо-приятствующих событию А, к числу n всех элементарных событий из
этой схемы:Согласно классическому определению подсчет вероятности события А сводится к подсчету числа благоприятствующих ему исходов. Делают это обычно комбинаторными методами.
Слайд 26Свойства вероятностей
1. Вероятность невозможного события равна нулю, т.е.
2. Достоверного
события равна единице, т.е.
3. Вероятность любого события не превосходит
единицы, т. е. 4. Сумма вероятностей противоположных событий равна единице, т.е.
Слайд 27Пример
В коробке имеются 10 шаров, которые различаются только цветом. Среди
этих 10 шаров 7 белых, остальные – черные.
Из коробки
взяли один шар. Найти вероятность того, что онбелый;
Черный;
Синий.
Слайд 28Пример
В коробке 5 синих, 4 красных и 3 зеленых карандаша.
Haудачу вынимают 3 карандаша. Какова вероятность того, что:
среди них 2
синих и 1 зеленый карандаш;Слайд 29Геометрическое определение вероятности
Геометрическое определение вероятности применяется в случае, когда исходы
опыта равновозможны, а ПЭС (или ) есть бесконечное несчетное множество.
Слайд 30 Рассмотрим на плоскости некоторую область , имеющую площадь , и
внутри области область D с площадью
Слайд 31 В области случайно выбирается точка X. Говорят: бросили точку
X в область .
При этом попадание точки в область
— достоверное событие, в D — случайное. Предполагается, что все точки области равноправны.
Рассмотрим событие A: брошенная точка попадет в область D.
Слайд 32 Геометрической вероятностью события A называется отношение площади области D к
площади области , т. е.
Геометрическое определение вероятности события применимо и
в случае, когда области D и обе линейные или объемные. Слайд 34 Геометрическая вероятность обладает всеми свойствами, присущими классическому (и другим) определению:
1.
Геометрическая вероятность любого события заключена между нулем и единицей.
2. Геометрическая
вероятность невозможного события равна нулю.3. Геометрическая вероятность достоверного события равна единице.