Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 13 Конденсированное состояние вещества
Содержание
- 1. Лекция 13 Конденсированное состояние вещества
- 2. 1. Условия равновесия фазМакроскопическая часть среды (вещества),
- 3. На границе раздела воды и пара происходит
- 4. 2. Явления на границе раздела газа, жидкости
- 5. Коэффициент пропорциональности α называется коэффициентом поверхностного натяжения.
- 6. Поверхностные явления возникают в связи с тем,
- 7. Итак, в поверхностном слое жидкости молекулы обладают
- 8. Силы поверхностного натяжения, когда поверхность жидкости не
- 9. Очевидно, геометрическая сумма составляющих ΔF2 для всего
- 10. В общем случае, когда поверхность жидкости отличается
- 11. 3. Смачивание. Капиллярные явления Рассмотрим теперь явления,
- 12. Если поверхностное натяжение на границе раздела жидкости
- 13. Для случая механического равновесия имеем F12 +
- 14. Если это условие не выполняется, капля либо,
- 15. Рассмотрим случай, когда капилляр погружен одним концом
- 16. Тогда имеемИз этой формулы следует, что при
- 17. 4. Диаграммы состояния При описании состояния вещества
- 18. В этой точке встречаются кривая плавления 1,
- 19. Вещество в трех различных агрегатных состояниях может
- 20. На рисунке схематически изображены области метастабильных состояний
- 21. Так как давление переохлажденного пара превышает давление
- 22. На рисунке изображены изотермы системы жидкость-газ, характерные
- 23. Так как в критической точке вещество представляет
- 24. Скачать презентанцию
1. Условия равновесия фазМакроскопическая часть среды (вещества), имеющая однородный физико-химический состав, называется фазой. При описании пространственно неоднородных сред применимо разбиение их на некоторое число фаз, разделенных границами раздела.Примером двухфазной системы может
Слайды и текст этой презентации
Слайд 1Лекция 13
Конденсированное состояние вещества.
1. Условия равновесия фаз
2. Явления на границе
раздела газа, жидкости и твердого тела
Слайд 21. Условия равновесия фаз
Макроскопическая часть среды (вещества), имеющая однородный физико-химический
состав, называется фазой. При описании пространственно неоднородных сред применимо разбиение
их на некоторое число фаз, разделенных границами раздела.Примером двухфазной системы может служить стеклянный сосуд с налитой в него водой. Это жидкая фаза (вода) и твердая фаза (стекло). Если в состав системы включить окружающий сосуд воздух, то система станет трехфазной. Третья фаза – газообразная (воздух). Отметим, что смесь газов является однофазной системой, так как в этом случае нет границы раздела.
Для равновесия фаз необходимо, чтобы между ними наблюдалось тепловое и механическое равновесие. Первое из этих условий означает равенство температур Т1 и Т2 с разных сторон границы раздела фаз. Второе условие можно записать так: Р2 = Р1 + ΔР12, где ΔР12 – дополнительное давление на первую фазу, создаваемое границей её раздела со второй.
В качестве многофазной системы может выступать система, состоящая из фаз одного и тоже вещества, находящегося в различных агрегатных состояниях. Примером такой ситуации может служить система, состоящая из воды, в которой плавает кусочек льда. В процессе таяния льда, границы раздела различных агрегатных состояний, изменяется, то есть к движению границ раздела фаз. При этом будет происходить процесс превращения вещества из одного агрегатного состояния в другое, то есть фазовое превращение.
Слайд 3На границе раздела воды и пара происходит постоянный процесс перехода
молекул из воды в пар и обратно. В равновесном состоянии
эти встречные процессы взаимно компенсируют друг друга, а при подводе или отводе теплоты один из этих процессов (переход молекул из воды в пар или наоборот) начинает преобладать и это приводит к изменению количества вещества в различных агрегатных состояниях.Уравнение Р = Р(Т) описывает кривую равновесия двух фаз. Если рассматривается граница раздела жидкости и газа, то это уравнение описывает кривую испарения. При описании границы раздела жидкости и твердого тела - рассматриваемое уравнение дает кривую плавления.
При фазовых превращениях производные некоторых термодинамических потенциалов в различных фазах могут быть различными. Если первые производные удельных термодинамических потенциалов для различных фаз не равны между собой, то такое фазовое превращение называется фазовым переходом первого рода. Характерной особенностью этих фазовых переходов является поглощение или выделение теплоты при их осуществлении. К фазовым переходам первого рода относятся превращения при испарении, конденсации, плавлении и кристаллизации вещества.
Если при фазовом превращении первые производные удельных термодинамических потенциалов для различных фаз одинаковы, а вторые производные различны, то такие превращения называются фазовыми переходами второго рода. При таких переходах теплота не выделяется и не поглощается, но для них характерны скачкообразные изменения теплоемкости, температурного коэффициента расширения и сжимаемости вещества. Примерами фазовых переходов второго рода являются превращение магнитного сплава из ферромагнитного состояния в парамагнитное, переход металла или сплава в сверхпроводящее состояние и переход жидкого гелия в сверхтекучее состояние.
Слайд 42. Явления на границе раздела газа, жидкости и твердого тела
Опыт показывает, что поверхность жидкости стремится принять такую форму, чтобы
иметь минимальную площадь. Это явление связано с воздействием на поверхность жидкости механических сил, стремящихся уменьшить площадь этой поверхности. Указанные силы называются силами поверхностного натяжения.Рассмотрим явления, возникающие на границе раздела жидкости и газа. Пусть имеется пленка жидкости (например, мыльная пленка), натянутая на рамку с одной подвижной перемычкой.
За счет сил поверхностного натяжения пленка будет стремиться уменьшить свою площадь. Для того, чтобы воспрепятствовать этому, к перемычке необходимо приложить силу F, величина которой, как показывает опыт, не зависит от площади пленки, а пропорциональна длине перемычки l:
F = 2αl.
Слайд 5Коэффициент пропорциональности α называется коэффициентом поверхностного натяжения. Двойка в формуле
означает, что пленка жидкости имеет две поверхности и если её
толщина много больше межмолекулярного расстояния, то происходит независимое воздействие двух поверхностей пленки на перемычку. Очевидно, что сила F равна силе поверхностного натяжения. Эта сила направлена по касательной к поверхности пленки.При медленном перемещении перемычки на величину dx, площадь поверхности пленки увеличивается на величину dSповерх = 2ldx.
Элементарная работа δА', которую необходимо совершить против сил поверхностного натяжения, определяется по формуле
δА' = Fdx = 2αldx = αdSповерх.
Работа dA = -dA', совершаемая силами поверхностного натяжения будет δА = -αdSповерх
Поверхностное натяжение численно равно работе, которую необходимо затратить при обратимом изотермическом процессе для увеличения площади поверхности жидкости на единицу. Указанная работа затрачивается на приращение энергии поверхности жидкости - свободной поверхностной энергии. Следовательно, поверхностное натяжение численно равно удельной (на единицу площади) свободной поверхностной энергии.
Слайд 6Поверхностные явления возникают в связи с тем, что молекулы в
толще жидкости и на ее поверхности находятся в неодинаковых условиях.
В толще жидкости каждая молекула испытывает притяжение со стороны всех соседних молекул, находящихся в пределах ее сферы молекулярного действия. В этом случае силы притяжения, действующие на молекулу со всех сторон, взаимно компенсируются и поэтому их равнодействующая в среднем равна нулю.Иначе обстоит дело с молекулами, находящимися от поверхности жидкости на расстояниях меньших, чем радиус молекулярного действия. В той части сферы молекулярного действия, которая выступает из жидкости, будет значительно меньше молекул, чем в остальной ее части, так как плотность пара или газа, с которым граничит жидкость, меньше плотности жидкости. Силы притяжения со стороны соседних молекул в этом случае уже не будут взаимно скомпенсированными и их равнодействующая в среднем отлична от нуля и направлена внутрь жидкости.
Для того, чтобы молекула переместилась из глубины жидкости в поверхностный слой, она должна совершить работу против сил, действующих в поверхностном слое.
Слайд 7Итак, в поверхностном слое жидкости молекулы обладают дополнительной потенциальной энергией.
Этот избыток энергии молекул жидкости, находящихся в поверхностном слое, по
сравнению с их энергией внутри остального объема жидкости, называют поверхностной энергией.В состоянии устойчивого равновесия жидкость стремится иметь минимальное значение свободной поверхностной энергии и принимает форму, при которой ее поверхность минимальна. Именно с этим и связана сферическая форма мелких капель и пузырьков. В состоянии невесомости такую же сферическую форму принимает и любая масса жидкости. В земных условиях форма крупных капель заметно отличается от сферической потому, что они сплющиваются под действием сил тяжести. Действием сил тяжести объясняют и те, что в земных условиях жидкости принимают форму сосуда, в который они налиты, т. е. жидкости стремятся принять такую форму, при которой их центр масс будет иметь наименьшее положение.
Единицу поверхностного натяжения можно определить в единицах энергии на единицу площади, или силы на единицу длины:
[α] = Дж/м2 = Н/м.
Поверхностное натяжение зависит от температуры. для сравнительно небольших интервалов температуры оно обычно убывает по линейному закону ростом температуры. Это объясняют тем, что с повышением температуры уменьшается различие в плотности жидкости и ее насыщенного пара. В критической точке, когда плотность жидкости и пара одинакова, поверхностное натяжение жидкости равно нулю.
Слайд 8Силы поверхностного натяжения, когда поверхность жидкости не плоская, создают дополнительное
давление к тому, которое испытывает жидкость с плоской поверхностью. При
выпуклой поверхности жидкости это дополнительное давление положительно, а при вогнутой отрицательно.Вычислим дополнительное давление для сферической поверхности жидкости радиусом R. Для этого рассечем мысленно жидкость плоскостью и выделим шаровой сегмент, ограниченный от остальной поверхности жидкости окружностью радиусом r = Rsinφ.
На каждый элемент длины Δl этой окружности в направлении, касательном к поверхности сегмента, действует сила поверхностного натяжения ΔF = αΔl.
Разложим силу ΔF на две составляющие, одна из которых лежит в плоскости сечения, а другая направлена перпендикулярно к ней. Эти составляющие силы будут соответственно равны
ΔF1 = ΔFsinφ и ΔF2 = ΔFcosφ
Слайд 9Очевидно, геометрическая сумма составляющих ΔF2 для всего периметра окружности, ограничивающей
рассматриваемый сегмент, будет равна нулю. Составляющие ΔF1 в сумме дадут
равнодействующую, направленную по нормали к плоскости сечения и равнуюРавнодействующая сил поверхностного натяжения будет прижимать рассматриваемый сегмент к остальной части жидкости по всей разделяющей их поверхности S = πr2. Значит, дополнительное давление внутри жидкости, создаваемое силами поверхностного натяжения и обусловленное кривизной ее поверхности, равно
Отметим, что поскольку в формулу не входит r, то, как и следовало ожидать, дополнительное давление ΔР не зависит от того, в каком месте поверхности Жидкости выделен шаровой сегмент.
Для вогнутой поверхности ее центр кривизны О лежит вне жидкости. Повторяя для этого случая весь предыдущий вывод, нетрудно найти, что
т. е. под вогнутой поверхностью давление внутри жидкости меньше, чем в случае плоской поверхности на ΔР.
Слайд 10В общем случае, когда поверхность жидкости отличается от сферической, кривизну
поверхности характеризуют средней кривизной, которая может иметь разное значение для
различных точек поверхности. Среднюю кривизну поверхности в данной точке определяют через кривизну нормальных сечений, т. е. через кривизну линий пересечения поверхности с взаимно перпендикулярными плоскостями, проходящими через нормаль к поверхности в рассматриваемой точке. При этом под кривизной кривой понимают величину, обратную ее - радиусу кривизны. Например, для сферы любое нормальное сечение представляет собой окружность радиусом R, а величина Н = 1/R будет ее кривизной. Полусумма обратных радиусов кривизны нормальных сечений и характеризует среднюю кривизну поверхности в данной точке:Лаплас доказал, что ΔР = 2αН справедлива для поверхности любой формы, где Н — средняя кривизна поверхности в той точке, под которой определяется дополнительное давление ΔР.
эта формула получила название формулы Лапласа.
Для плоской поверхности R1 и R2 ≈ ∞, а следовательно и дополнительное давление ΔР, будет равно нулю.
Слайд 113. Смачивание. Капиллярные явления
Рассмотрим теперь явления, происходящие с каплей
жидкости, помещенной на поверхность твердого тела. В этом случае имеются
три границы раздела между фазами: газ-жидкость, жидкость-твердое тело и газ-твердое тело. Поведение капли жидкости будет определяться значениями поверхностного натяжения (удельными величинами свободной поверхностной энергии) на указанных границах раздела. Сила поверхностного натяжения на границе раздела жидкости и газа будет стремиться придать капле сферическую форму. Это произойдет в том случае, если поверхностное натяжение на границе раздела жидкости и твердого тела будет больше поверхностного натяжения на границе раздела газа и твердого тела. В этом случае процесс стягивания жидкой капли в сферу приводит к уменьшению площади поверхности границы раздела жидкость-твердое тело при одновременном увеличении площади поверхности границы раздела газ-жидкость. Тогда наблюдается несмачивание поверхности твердого тела жидкостью. Форма капли будет определяться равнодействующей сил поверхностного натяжения и силы тяжести. Если капля большая, то она будет растекаться по поверхности, а если маленькая - стремиться к шарообразной форме.Слайд 12Если поверхностное натяжение на границе раздела жидкости и твердого тела
меньше поверхностного натяжения на границе раздела газа и твердого тела,
то капля приобретет такую форму, чтобы уменьшить площадь поверхности границы раздела газ-твердое тело, то есть будет растекаться по поверхности тела. В этом случае наблюдается смачивание жидкостью твердого тела.Для количественного описания смачивания жидкостью твердого тела рассмотрим равновесие сил, действующих на элемент l контура, образованного пересечением трех границ раздела фаз: газа 1, жидкости 2 и твердого тела 3.
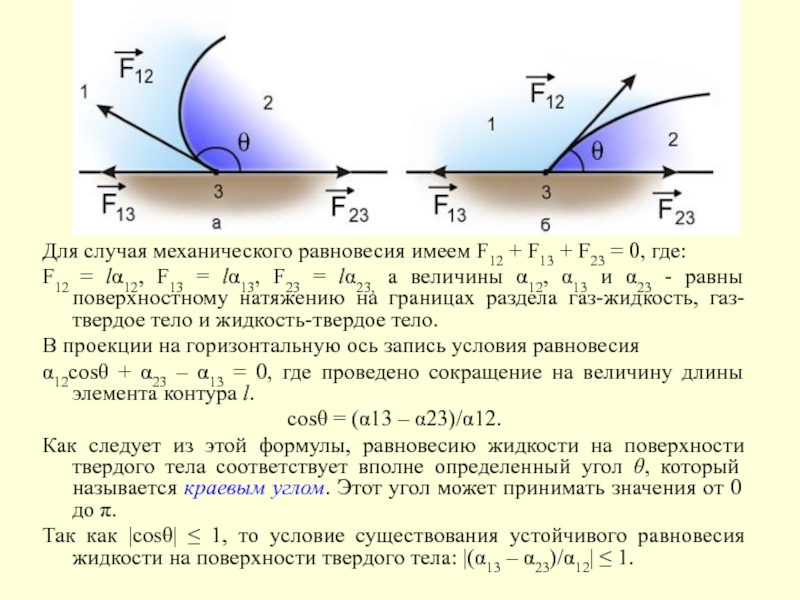
Слайд 13Для случая механического равновесия имеем F12 + F13 + F23
= 0, где:
F12 = lα12, F13 = lα13, F23
= lα23, а величины α12, α13 и α23 - равны поверхностному натяжению на границах раздела газ-жидкость, газ-твердое тело и жидкость-твердое тело.В проекции на горизонтальную ось запись условия равновесия
α12cosθ + α23 – α13 = 0, где проведено сокращение на величину длины элемента контура l.
cosθ = (α13 – α23)/α12.
Как следует из этой формулы, равновесию жидкости на поверхности твердого тела соответствует вполне определенный угол θ, который называется краевым углом. Этот угол может принимать значения от 0 до π.
Так как |cosθ| ≤ 1, то условие существования устойчивого равновесия жидкости на поверхности твердого тела: |(α13 – α23)/α12| ≤ 1.
Слайд 14Если это условие не выполняется, капля либо, при
(α13 –
α23)/α12 > 1,
начинает неограниченно (до толщины нескольких мономолекулярных слоев)
растекаться по поверхности, либо, при (α13 – α23)/α12 < -1,
стягиваться до тех пор, пока её общая граница с поверхностью не превратится в точку. В первом случае наблюдается явление полного смачивания твердого тела жидкостью (например, капля керосина на поверхности стекла), а во втором - полное несмачиваение (например, капля воды на поверхности парафина). Если краевой угол 0 < θ < π/2, то имеет место частичное смачивание, а при π/2 < θ < π - частичное несмачивание.
Явление смачивания (или несмачивания) твердого тела жидкостью приводит к появлению капиллярного эффекта. Капилляром называется тонкая трубка, вставленная в сосуд с жидкостью. Капиллярный эффект связан с тем, что в зависимости от того, смачивает жидкость стенки капилляра или нет, внутри капилляра поверхность жидкости приобретает соответственно вогнутую или выпуклую форму. В первом случае давление внутри жидкости уменьшается по сравнению с внешним, и она поднимается внутри капилляра. А во втором - это давление возрастает, что приводит к опусканию уровня жидкости в капилляре по отношению к её уровню в сосуде.
Слайд 15Рассмотрим случай, когда капилляр погружен одним концом в жидкость, налитую
в широкий сосуд. Если капилляр представляет собой круглую цилиндрическую трубку
с радиусом канала r и жидкость смачивает его стенки, то мениск в нем будет иметь сферическую форму.Под этим мениском давление жидкости будет на ΔР меньше, чем в широком сосуде, где поверхность жидкости практически плоская. Поэтому в капилляре жидкость поднимается на высоту h, при которой вес столба жидкости в нем уравновесит отрицательное дополнительное давление, обусловленное кривизной мениска: ΔP = ρgh, где .
Из рисунка видно, что
и, следовательно,
Слайд 16Тогда имеем
Из этой формулы следует, что при 0 < θ
< π/2 уровень жидкости в капилляре повышается, а при π/2
< θ < π - соответственно понижается.Таким образом, высота поднятия смачивающей жидкости в капилляре тем больше, чем меньше его радиус, т. е. чем уже капилляр. Очевидно, эта же формула позволяет определить и глубину опускания в капилляре несмачивающей жидкости.
Одна и та же жидкость смачивает одни твердые тела и не смачивает другие. Например, вода смачивает стекло и не смачивает парафин; ртуть не смачивает стекло и смачивает чистую поверхность железа.
Слайд 174. Диаграммы состояния
При описании состояния вещества и его фазовых
переходов обычно используются переменные P и T, в которых изображаются
кривые равновесия при фазовых переходах данного вещества. Диаграмма, построенная в этих переменных, называется диаграммой состояния. Каждой точке на этой диаграмме соответствует определенное равновесное состояние. Она позволяет определить, какие фазовые переходы происходят при тех или иных процессах.Рассмотрим случай термодинамической системы, в которой в равновесии находятся сразу три фазы однородного по физико-химическим свойствам вещества (например: лед, вода и пар). Равновесие такой системы будет наблюдаться при одновременном выполнении трех условий, соответствующих равновесию этих фаз между собой:
φ1(P,T) = φ2(P,T) = φ3(P,T). Или φ1(P,T) = φ2(P,T), φ2(P,T) = φ3(P,T).
Решение этой системы уравнений при условии отсутствия химических превращений дает совершенно определенные значения давления Pmp и температуры Tmp, при которых три фазы могут существовать одновременно. Точка на диаграмме состояния в переменных Р и Т, соответствующая указанным значениям давления и температуры, называется тройной точкой.
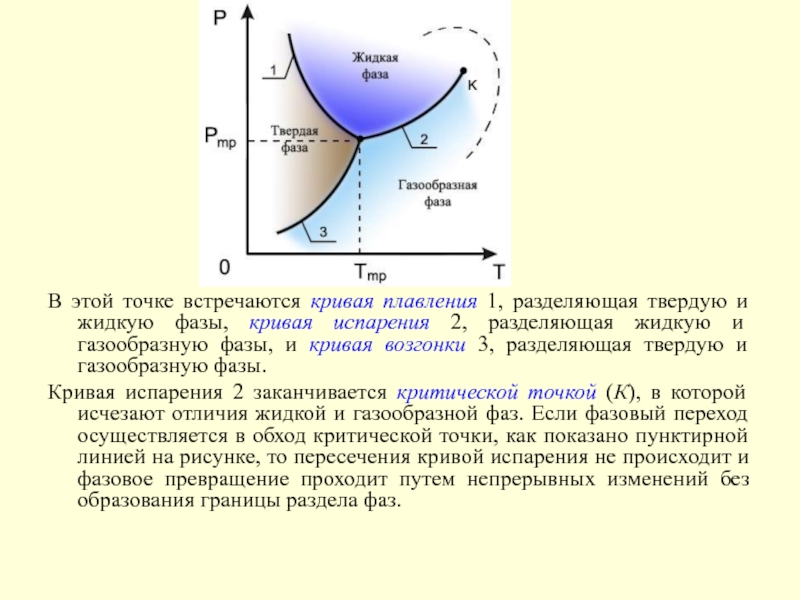
Слайд 18В этой точке встречаются кривая плавления 1, разделяющая твердую и
жидкую фазы, кривая испарения 2, разделяющая жидкую и газообразную фазы,
и кривая возгонки 3, разделяющая твердую и газообразную фазы.Кривая испарения 2 заканчивается критической точкой (К), в которой исчезают отличия жидкой и газообразной фаз. Если фазовый переход осуществляется в обход критической точки, как показано пунктирной линией на рисунке, то пересечения кривой испарения не происходит и фазовое превращение проходит путем непрерывных изменений без образования границы раздела фаз.
Слайд 19Вещество в трех различных агрегатных состояниях может наблюдаться и при
значениях температуры и давления, не соответствующих тройной точке. Например, в
природе при различных погодных условиях наблюдаются одновременно лед, вода и водяной пар (последний, как правило, косвенным образом). Однако, в отличие от состояния в тройной точке, указанные состояния не являются равновесными, и для них характерен постоянный переход вещества из одной фазы в другую.Значения давления и температуры в тройной точке для различных веществ очень стабильны, что позволяет использовать тройную точку для калибровки различных температурных шкал. Тройная точка воды используется в качестве основной реперной точки для температурных шкал Кельвина и Цельсия.
Как правило, все твердые вещества имеют несколько фазовых состояний, обусловленных различными кристаллическими модификациями, структурно отличающимися между собой. Эти фазы могут точно так же находиться в состоянии равновесия между собой, как и фазы, связанные с различными агрегатными состояниями. На диаграмме состояния условиям равновесия этих фаз соответствуют кривые равновесия при фазовых переходах.
Для различных кристаллических модификаций характерно существование метастабильных состояний, то есть таких состояний, при которых одна фаза существует в области температур и давлений другой фазы. Такие же метастабильные состояния существуют и для фазовых переходов из одного агрегатного состояния в другое вблизи тройной точки.
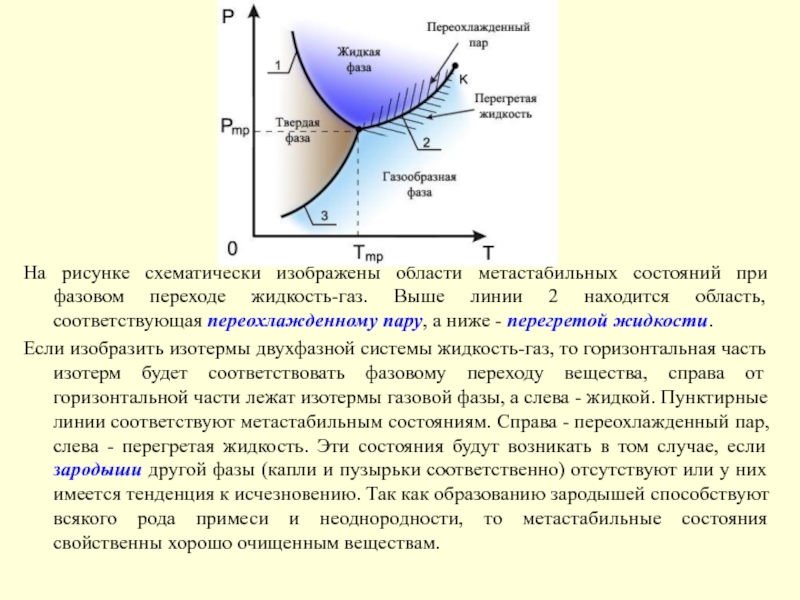
Слайд 20На рисунке схематически изображены области метастабильных состояний при фазовом переходе
жидкость-газ. Выше линии 2 находится область, соответствующая переохлажденному пару, а
ниже - перегретой жидкости.Если изобразить изотермы двухфазной системы жидкость-газ, то горизонтальная часть изотерм будет соответствовать фазовому переходу вещества, справа от горизонтальной части лежат изотермы газовой фазы, а слева - жидкой. Пунктирные линии соответствуют метастабильным состояниям. Справа - переохлажденный пар, слева - перегретая жидкость. Эти состояния будут возникать в том случае, если зародыши другой фазы (капли и пузырьки соответственно) отсутствуют или у них имеется тенденция к исчезновению. Так как образованию зародышей способствуют всякого рода примеси и неоднородности, то метастабильные состояния свойственны хорошо очищенным веществам.
Слайд 21Так как давление переохлажденного пара превышает давление насыщенного пара при
той же температуре, то такой пар называется пересыщенным.
Опыты, проведенные в
середине XIX века показали, что если в паре содержатся частицы пыли, то даже при небольшом пересыщении образуется туман и происходит переход из точки А в точку В. Такой процесс происходит в атмосфере, когда потоки, вызванные конвекцией, поднимают вверх воздух, содержащий водяной пар, где происходит его расширение, сопровождающееся уменьшением температуры. Это приводит к возникновению тумана и росту дождевых капель за счет избыточной концентрации пара по сравнению с насыщенным состоянием.Метастабильные состояния системы жидкость-газ наблюдаются в областях параметров, близких к кривой испарения. С повышением температуры плотность насыщенного пара возрастает и при некоторой температуре плотность пара становится равной плотности жидкости. Температура, при которой это происходит, называется температурой абсолютного кипения. При этом исчезает различие между жидкой и газообразной фазами, и кривая испарения заканчивается критической точкой К. Такое состояние, которое характеризуется определенным набором значений температуры Ткр, давления Ркр и объема Vкр, получило название критического состояния.
Слайд 22На рисунке изображены изотермы системы жидкость-газ, характерные для реальных веществ
и подтвержденные многочисленными опытами. Горизонтальный участок этих изотерм, соответствующий одновременному
существованию жидкой и газообразной фаз, с ростом температуры уменьшается. Точка, где длина горизонтального участка обращается в нуль и есть критическая точка К, а соответствующая ей температура - критическая температура Ткр.Переход из жидкого состояния в газообразное (или, наоборот, из газообразного в жидкое) может быть осуществлен по траектории, огибающей критическую точку без пересечения кривой испарения (пунктирная линия на рисунке). В этом случае фазового перехода первого рода с характерным для него скачком первых производных удельного термодинамического потенциала наблюдаться не будет. Переход из жидкого в газообразное состояние будет происходить путем непрерывных изменений без образования границы раздела фаз. При этом среда представляет собой однородную структуру, которая постепенно превращается из жидкости в газ или наоборот. То есть свойства фазы в этом случае меняются непрерывным образом.
Слайд 23Так как в критической точке вещество представляет собой смесь постоянно
флуктуирующих зародышей обеих фаз, то в случае наблюдения прозрачного вещества
при его прохождении через критическую точку, оно становится мутным. Это позволяет применять оптические методы для исследования свойств веществ в критической точке.Если переход осуществляется через кривую испарения, то можно наблюдать движение границы раздела жидкость-газ. Будет происходить изменение количества вещества в каждой фазе, при этом свойства фаз остаются неизменными (в случае изотермического перехода).
Непрерывный переход из жидкой фазы в газообразную (или наоборот) возможен потому, что между этими фазами нет принципиальной разницы. Они отличаются только подвижностью молекул. И в жидкости, и в газах молекулы могут совершать хаотическое поступательное движение.
При переходе жидкости в твердое состояние может наблюдаться метастабильное состояние - переохлажденная жидкость. В таком состоянии в частности может находиться вода, охлажденная до температуры ниже 0 оС. Если в таком состоянии в воде возникают зародыше твердой фазы, например, вследствие резкого изменения внешнего давления (при ударе по сосуду, в котором находится переохлажденная вода), то наблюдается очень быстрое превращение воды в лед.