Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 17
Содержание
- 1. Лекция 17
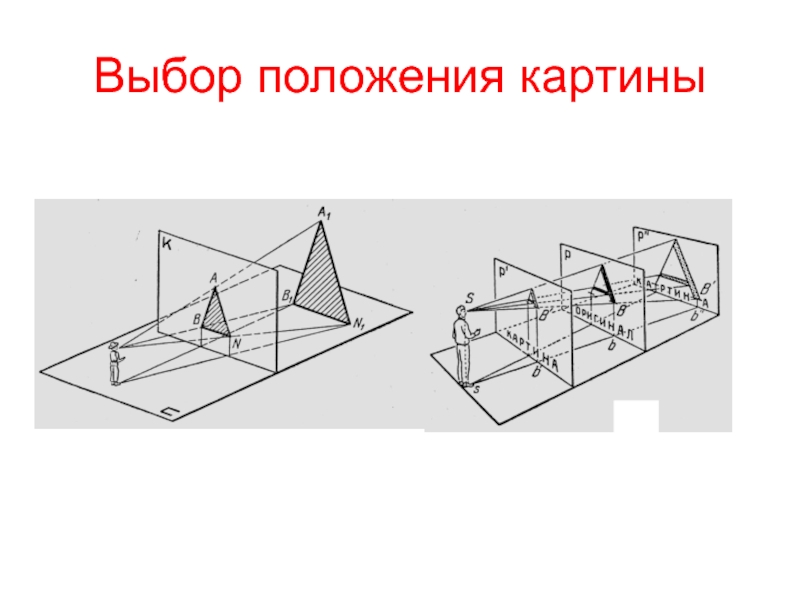
- 2. Выбор положения картиныКартина может располагаться :перед объектом;
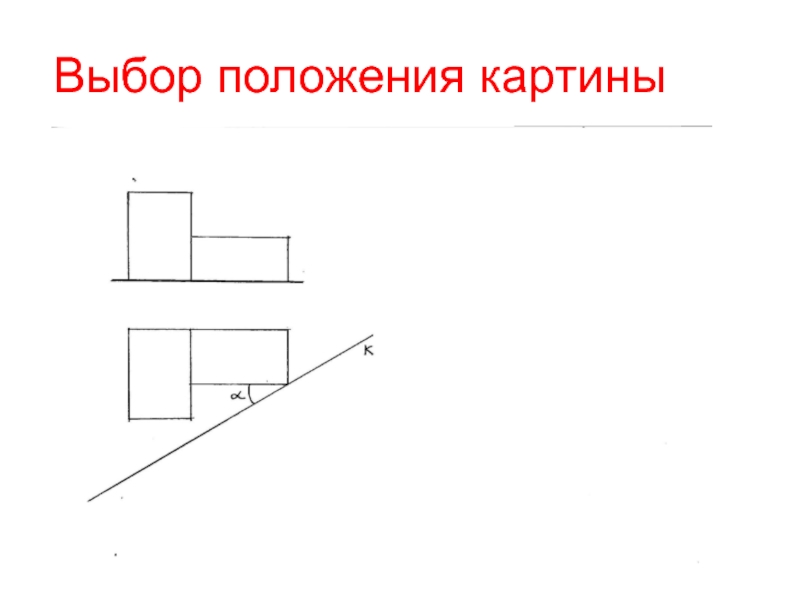
- 3. Выбор положения картины
- 4. Выбор положения картины
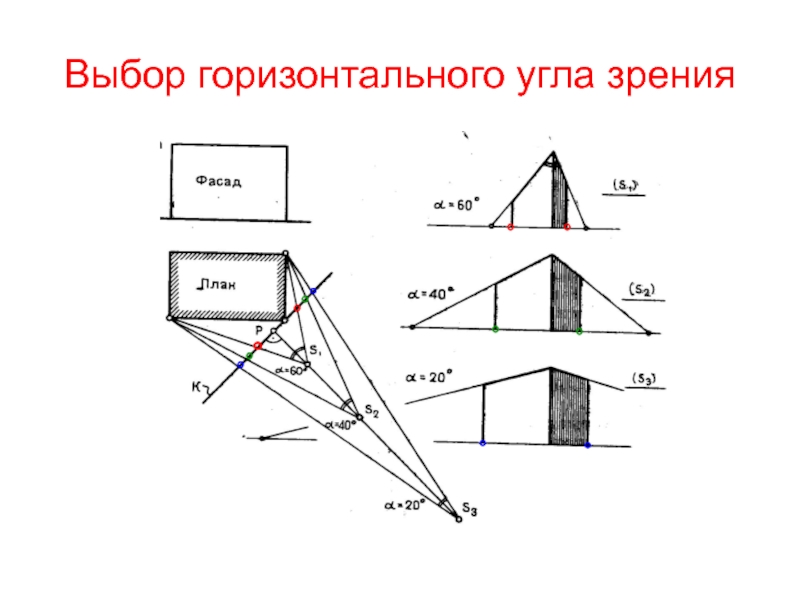
- 5. Выбор горизонтального угла зрения°°°°°°°°°°°°
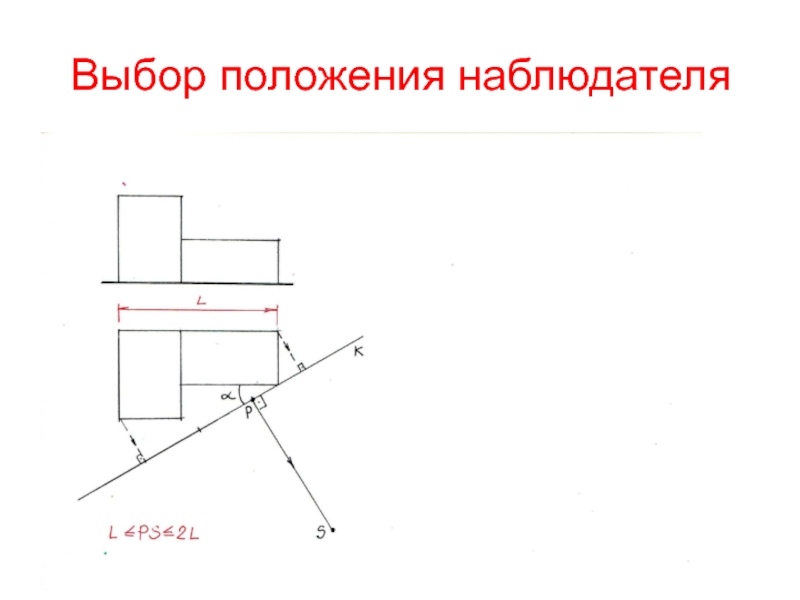
- 6. Выбор положения наблюдателяУгол зрения φ= от 20°
- 7. Выбор положения наблюдателя
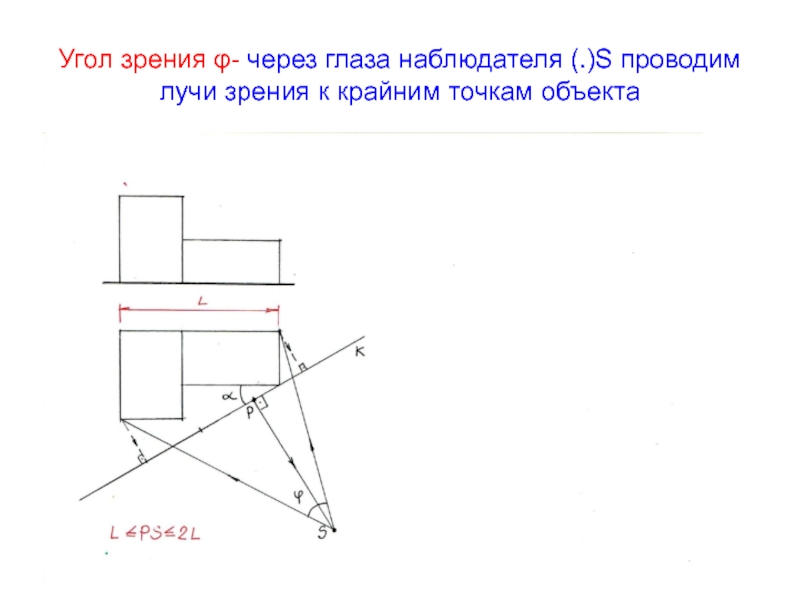
- 8. Угол зрения φ- через глаза наблюдателя (.)S проводим лучи зрения к крайним точкам объекта
- 9. Построение точек схода прямыхЧтобы построить точку схода
- 10. Построение точек схода
- 11. Выбор положения линии горизонтаЛиния горизонта может располагаться
- 12. Выбор положения линии горизонта
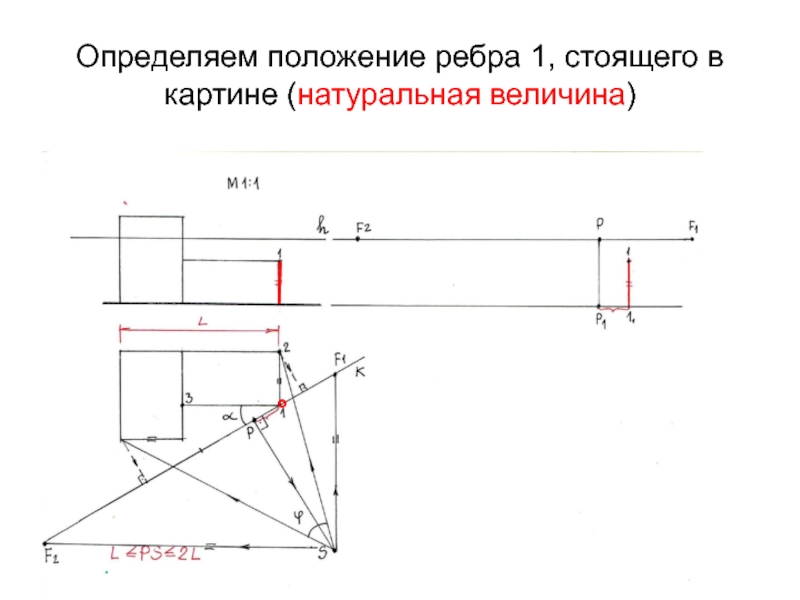
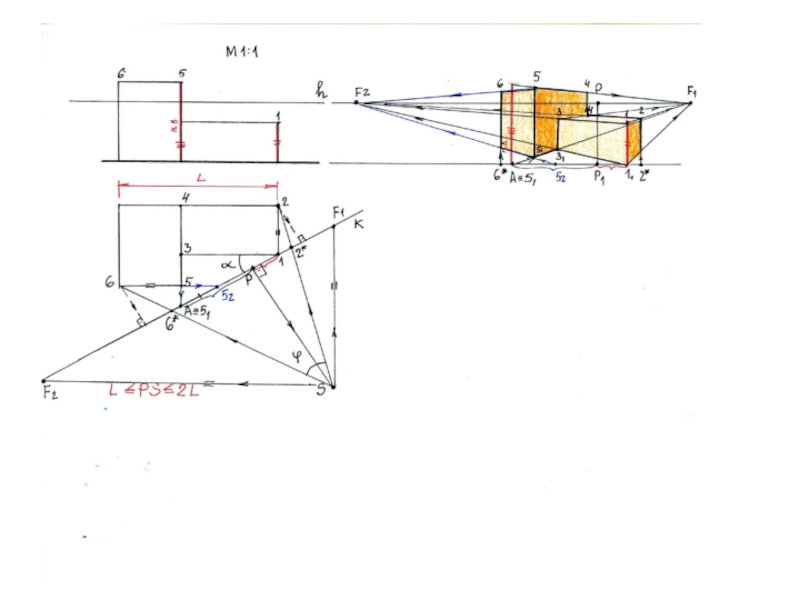
- 13. Определяем положение ребра 1, стоящего в картине (натуральная величина)°
- 14. Через данное ребро проходят две плоскости (в
- 15. Перспектива(.) 3 может быть получена путем построения перспектив пересекающихся прямых плана 3-1 и 3-А. °°
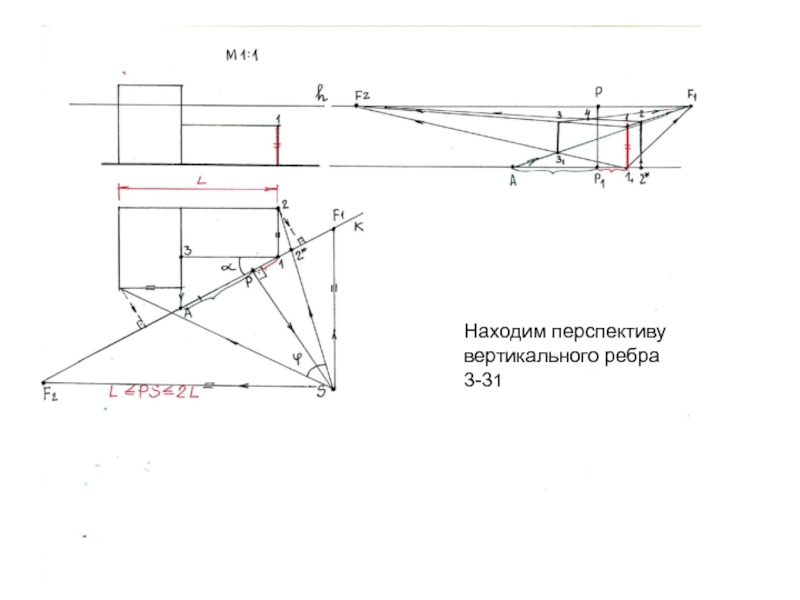
- 16. Находим перспективувертикального ребра3-31
- 17. Вытягиваем плоскость, проходящую через ребро 5 плана
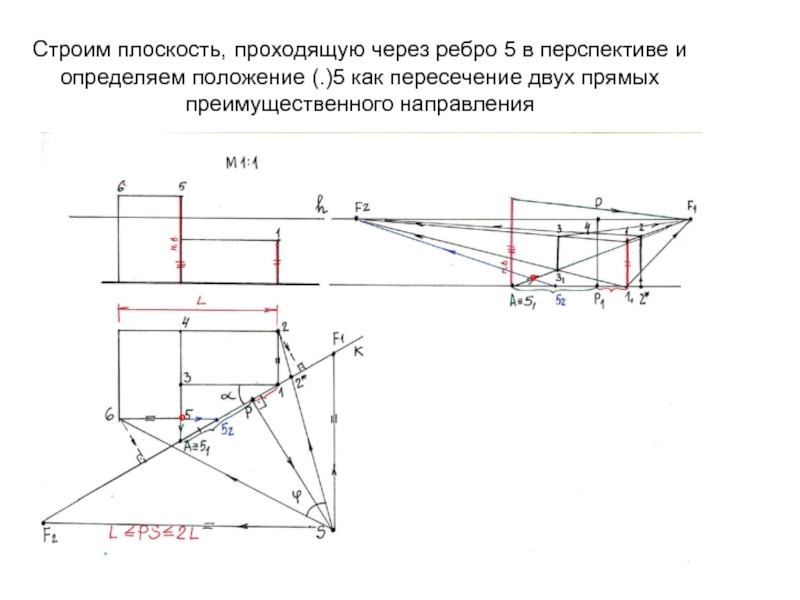
- 18. Строим плоскость, проходящую через ребро 5 в
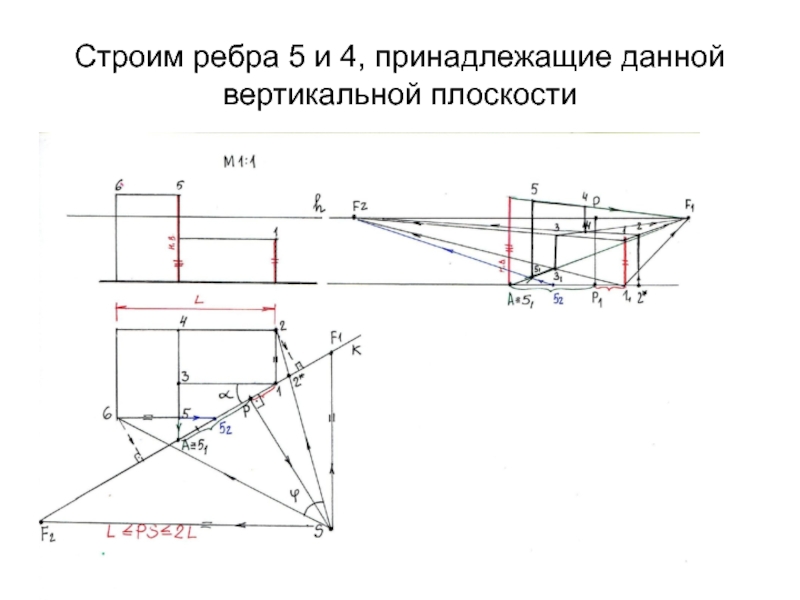
- 19. Строим ребра 5 и 4, принадлежащие данной вертикальной плоскости
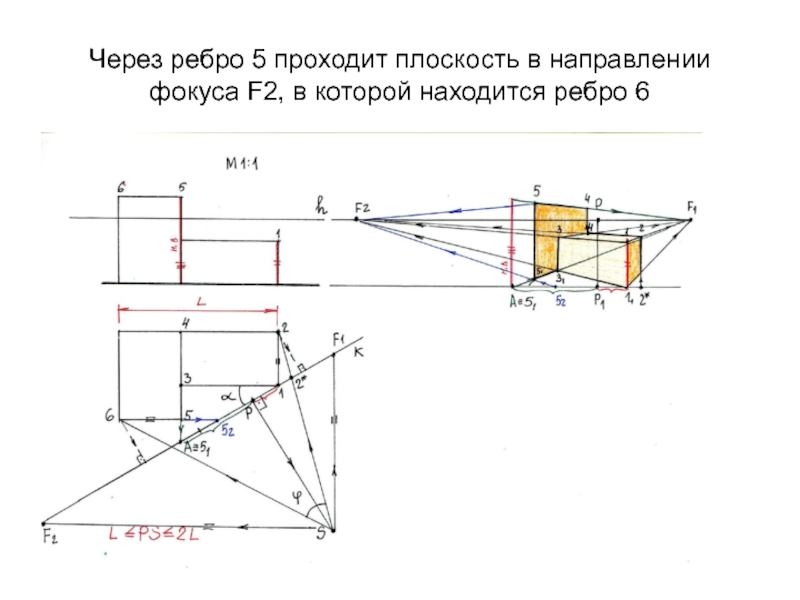
- 20. Через ребро 5 проходит плоскость в направлении фокуса F2, в которой находится ребро 6
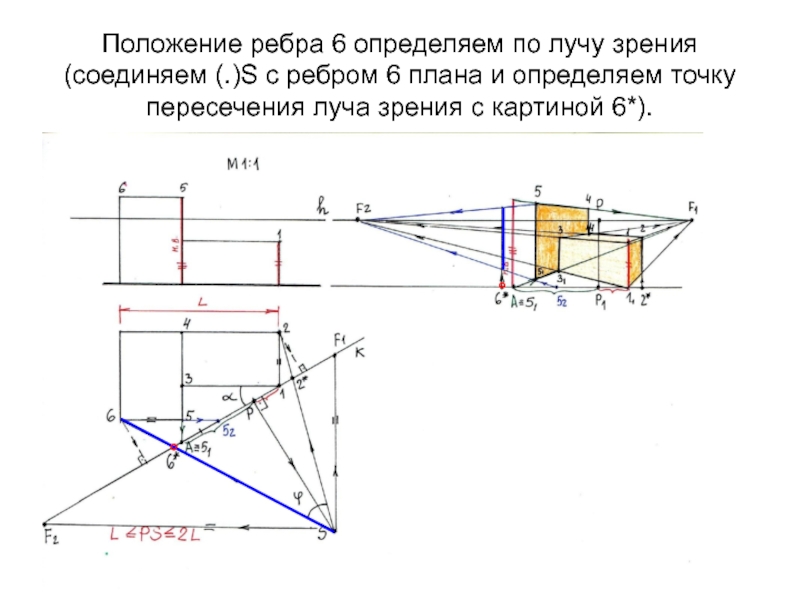
- 21. Положение ребра 6 определяем по лучу зрения
- 22. Слайд 22
- 23. Построение перспективы объекта с помощью прямых, перпендикулярных
- 24. Для построения перспективы объекта можно использовать разные
- 25. Построение перспективы объекта с помощью прямой преимущественного направления плана и луча зрения
- 26. Построение перспективы объекта с помощью прямых преимущественного
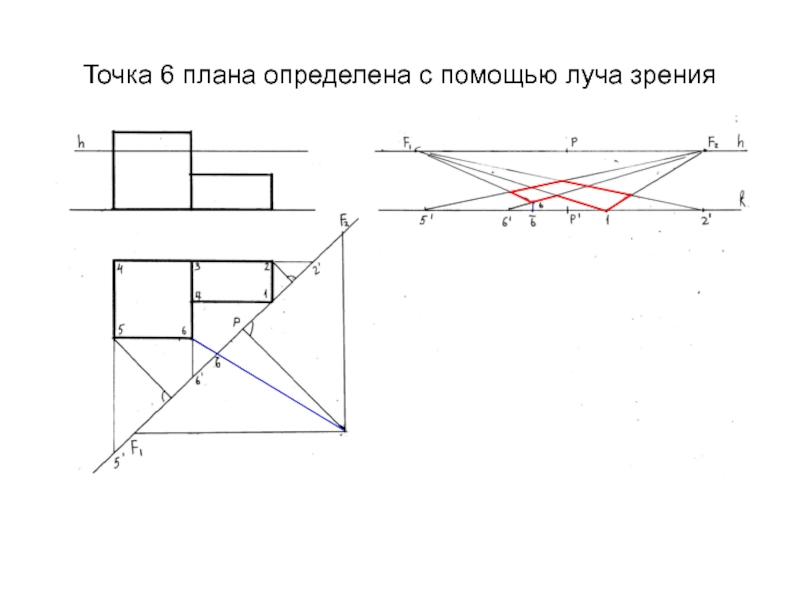
- 27. Точка 6 плана определена с помощью луча зрения
- 28. Построение перспективы точки с помощью перпендикулярной прямой
- 29. Пропорциональное деление отрезка прямой(теорема Фалеса)hhOkA'B‘1C‘1E‘1L'1M'1Задача: разделить отрезки в пропорции 2:3
- 30. Пропорциональное деление отрезка прямой(теорема Фалеса)hhOkA'B‘1C‘1E‘1L'1M'1Через конец отрезка
- 31. Пропорциональное деление отрезка прямой(теорема Фалеса)hhOkA'B‘1C‘1E‘1L'1M'1В этом случае
- 32. Пропорциональное деление отрезка прямой(теорема Фалеса)hhOkA'B‘1C‘1E‘1L'1M'1°F°°°°°Соединим конец пропорции
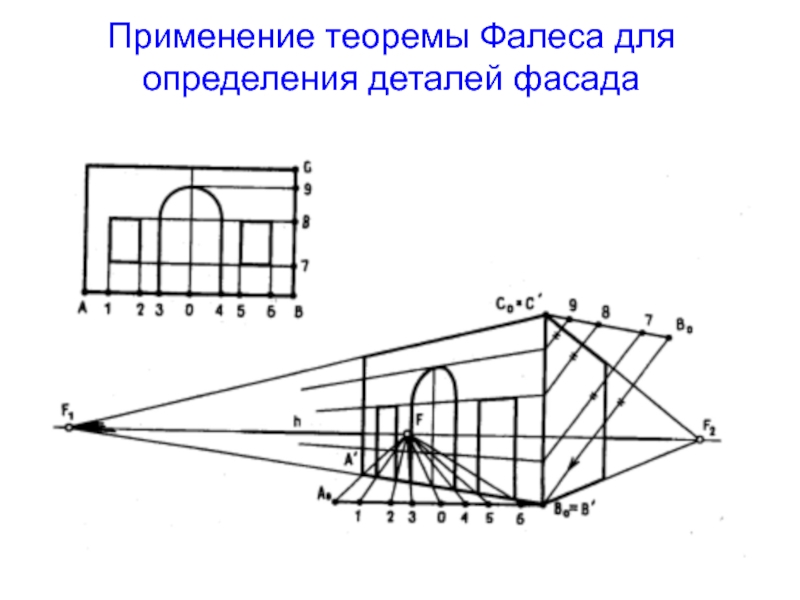
- 33. Применение теоремы Фалеса для определения деталей фасада
- 34. Скачать презентанцию
Выбор положения картиныКартина может располагаться :перед объектом; проходить через ребро объекта;За объектомУгол наклона к плоскости главного фасада α=30°
Слайды и текст этой презентации
Слайд 1Лекция 17
Построение перспективы объекта методом архитекторов с двумя точками схода
Определение
положения наблюдателя (точки зрения)
схода прямых преимущественных направлений плана
Слайд 2Выбор положения картины
Картина может располагаться :
перед объектом;
проходить через ребро
объекта;
За объектом
Угол наклона к плоскости главного фасада α=30°
Слайд 6Выбор положения наблюдателя
Угол зрения φ= от 20° до 60°. Данное
значение получается, если дистанционное расстояние L≤ PS ≤ 2L, где
L-длина объектаЧтобы получить угол зрения, близкий оптимальному, надо на плане из концов объекта опустить к картине перпендикуляры, полученное расстояние разделить на три части. Затем выбрать точку Р (1 часть относится к боковому фасаду, 2 части- к главному) и в ней восстановить перпендикуляр к картине и отложить дистанционное расстояние
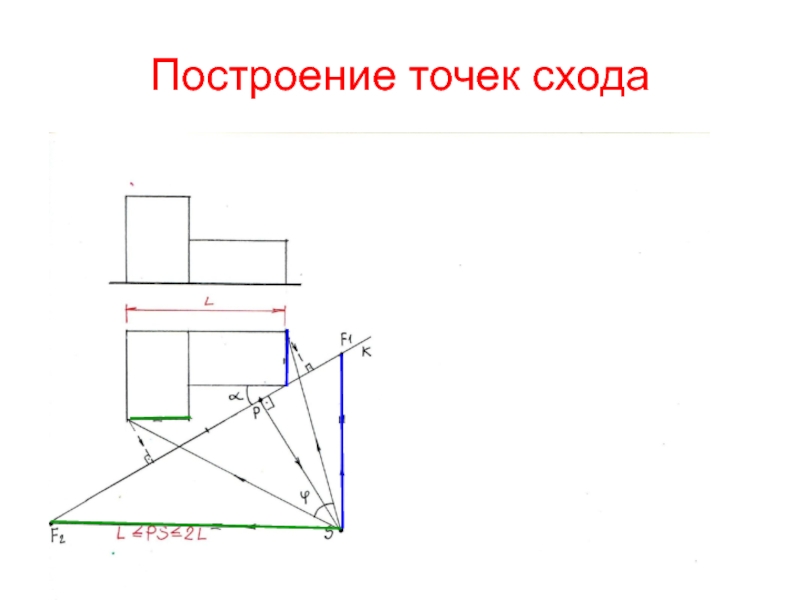
Слайд 9Построение точек схода прямых
Чтобы построить точку схода любой прямой, необходимо
через глаза наблюдателя (точку S) провести прямую, параллельную данной прямой
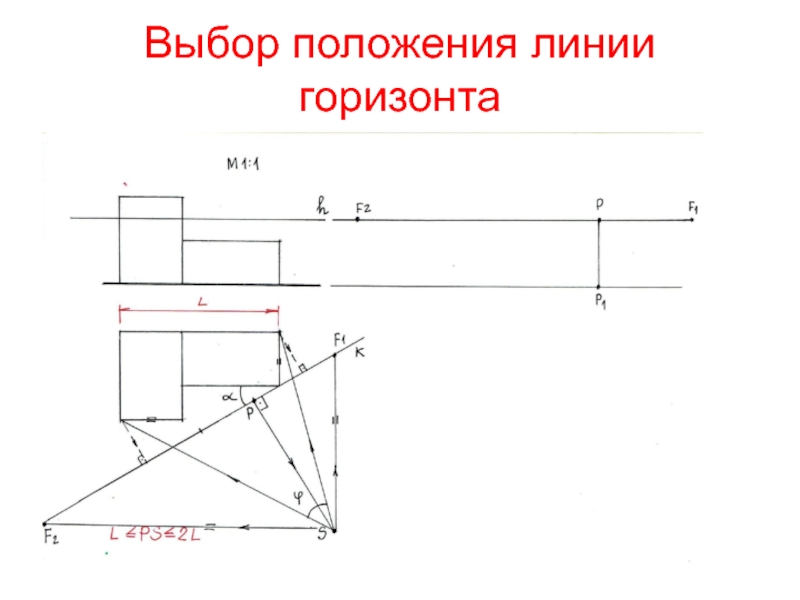
и найти ее пересечение с картиной
Слайд 11Выбор положения линии горизонта
Линия горизонта может располагаться на любой высоте
в зависимости от положения глаз наблюдателя.
Отметим 3 наиболее применяемых
положений линии горизонта:На высоте 1,7 м(уровень глаз человека)
С высоты птичьего полета (100 и более м)
Может совпадать или быть ниже основания картины
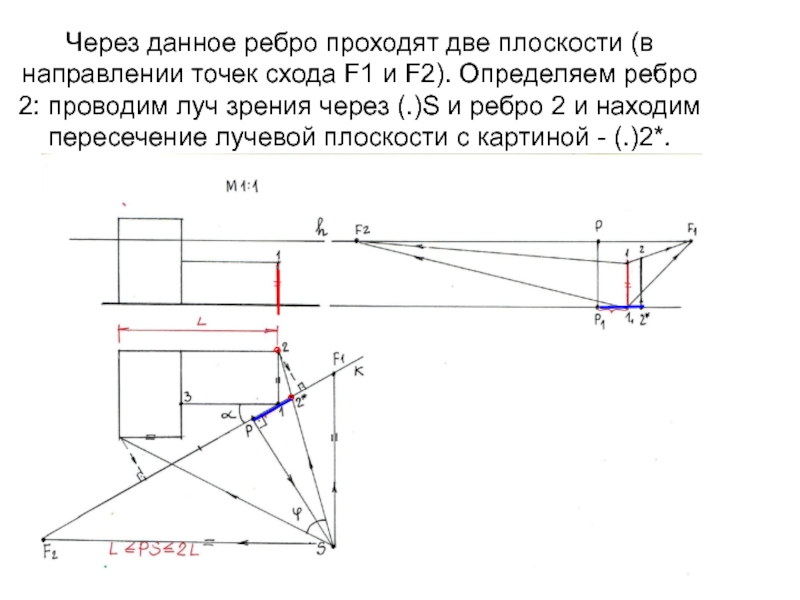
Слайд 14Через данное ребро проходят две плоскости (в направлении точек схода
F1 и F2). Определяем ребро 2: проводим луч зрения через
(.)S и ребро 2 и находим пересечение лучевой плоскости с картиной - (.)2*.°
°
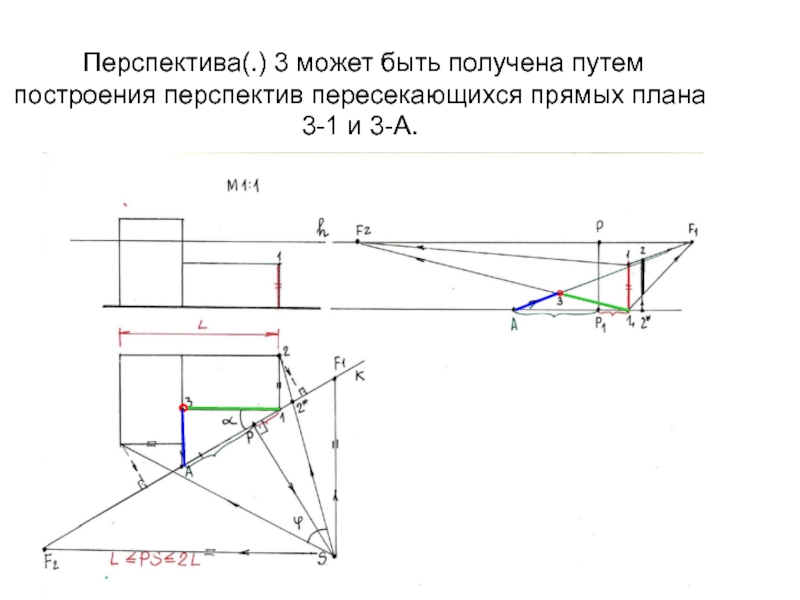
Слайд 15 Перспектива(.) 3 может быть получена путем построения перспектив пересекающихся
прямых плана 3-1 и 3-А.
°
°
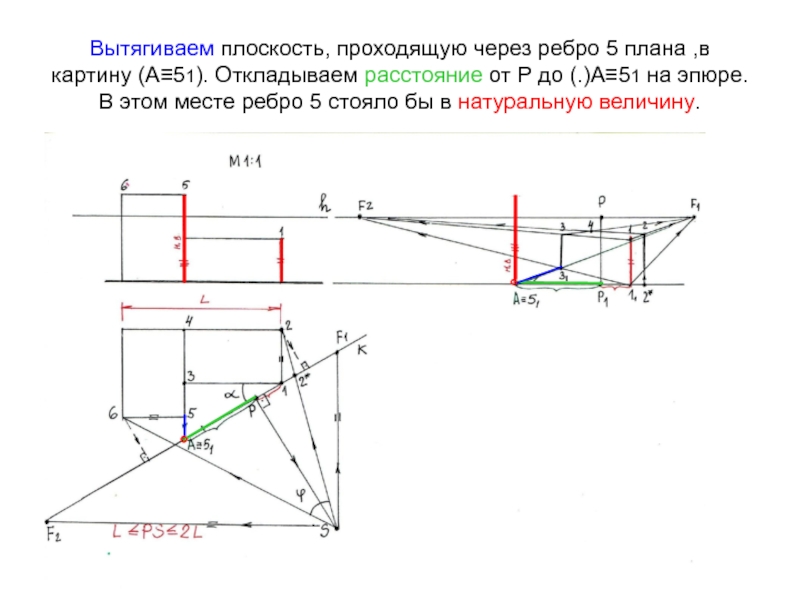
Слайд 17Вытягиваем плоскость, проходящую через ребро 5 плана ,в картину (А≡51).
Откладываем расстояние от Р до (.)А≡51 на эпюре. В этом
месте ребро 5 стояло бы в натуральную величину.°
°
Слайд 18Строим плоскость, проходящую через ребро 5 в перспективе и определяем
положение (.)5 как пересечение двух прямых преимущественного направления
°
°
Слайд 21Положение ребра 6 определяем по лучу зрения (соединяем (.)S с
ребром 6 плана и определяем точку пересечения луча зрения с
картиной 6*).°
°
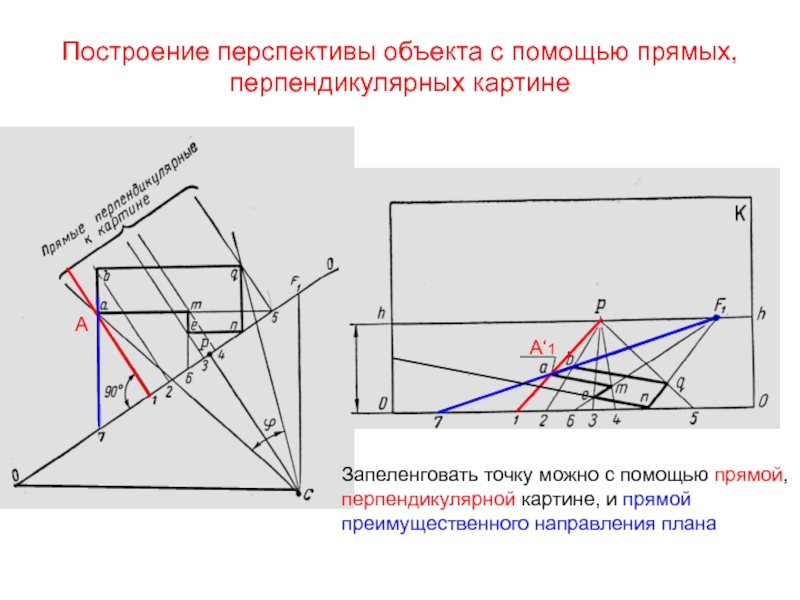
Слайд 23Построение перспективы объекта с помощью прямых, перпендикулярных картине
А
А‘1
Запеленговать точку
можно с помощью прямой,
перпендикулярной картине, и прямой преимущественного направления плана
Слайд 24Для построения перспективы объекта можно использовать разные приемы:
Пеленговать точки объекта
с помощью:
прямых преимущественного направления плана
Прямых, перпендикулярных картине и проходящих
к ней под углом 45°Прямой преимущественного направления плана и луча зрения, проходящего через точку зрения S и заданную точку
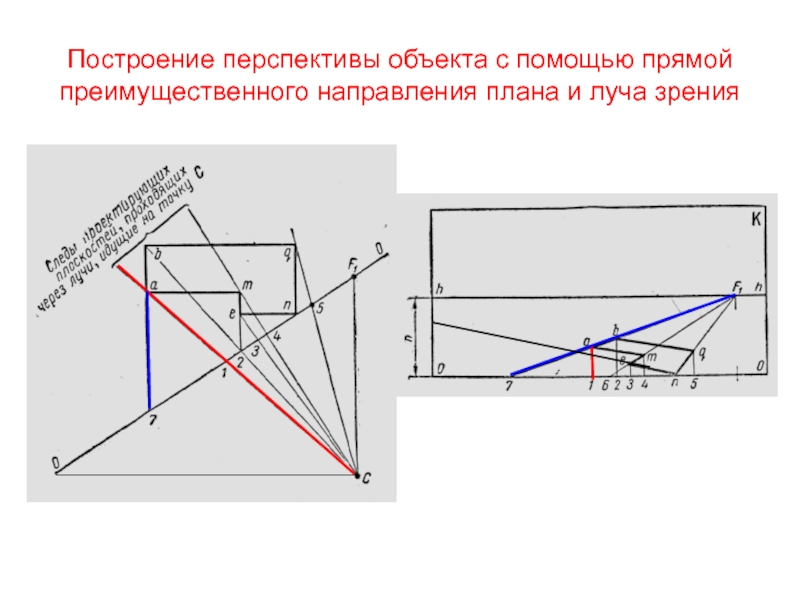
Слайд 25Построение перспективы объекта с помощью прямой преимущественного направления плана и
луча зрения
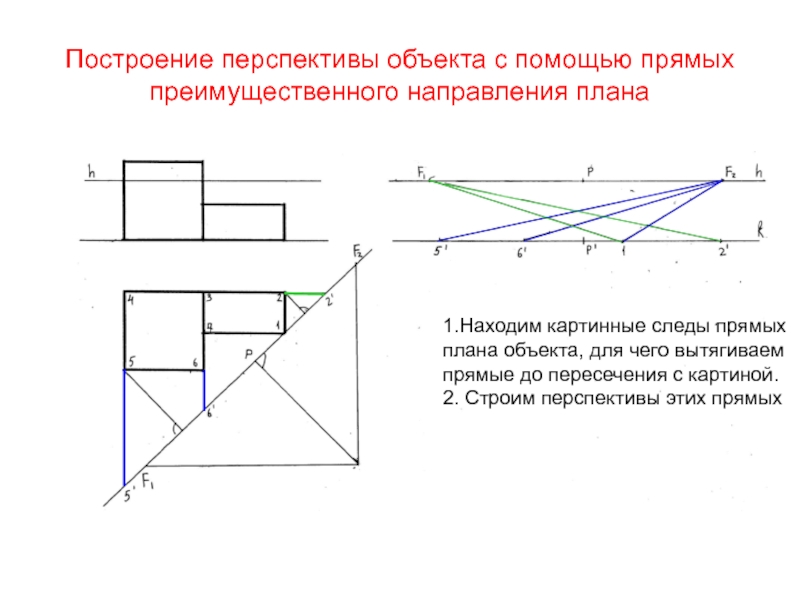
Слайд 26Построение перспективы объекта с помощью прямых преимущественного направления плана
1.Находим картинные
следы прямых
плана объекта, для чего вытягиваем прямые до пересечения с
картиной.2. Строим перспективы этих прямых
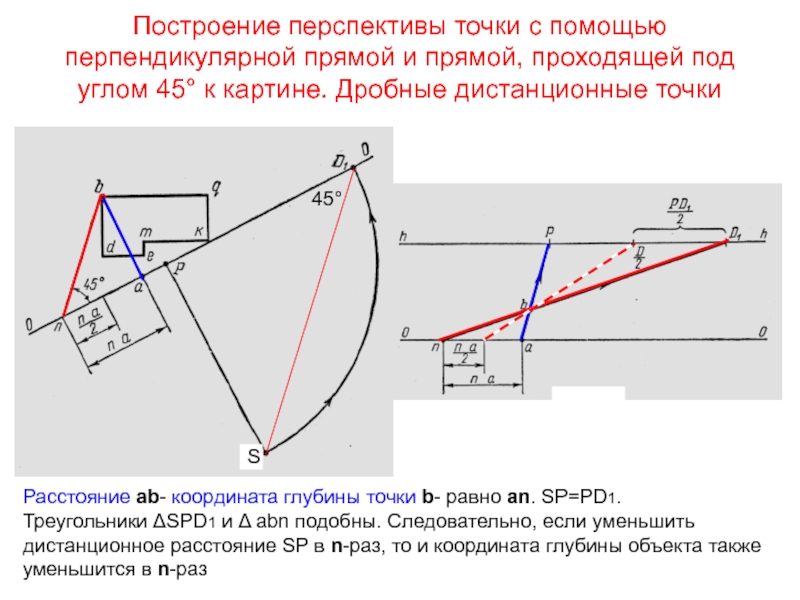
Слайд 28Построение перспективы точки с помощью перпендикулярной прямой и прямой, проходящей
под углом 45° к картине. Дробные дистанционные точки
°
Расстояние ab- координата
глубины точки b- равно аn. SP=PD1. Треугольники ΔSPD1 и Δ abn подобны. Следовательно, если уменьшить дистанционное расстояние SP в n-раз, то и координата глубины объекта также уменьшится в n-раз
S
45°
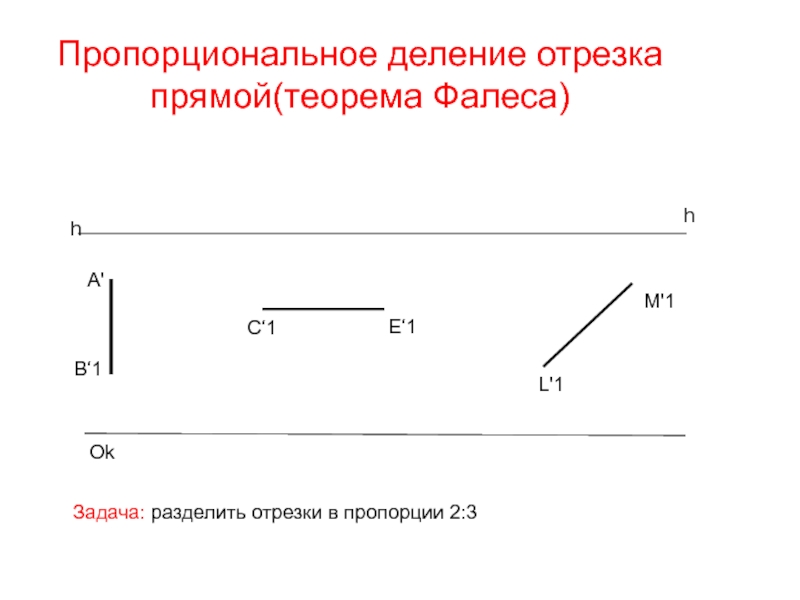
Слайд 29Пропорциональное деление отрезка прямой(теорема Фалеса)
h
h
Ok
A'
B‘1
C‘1
E‘1
L'1
M'1
Задача: разделить отрезки в пропорции 2:3
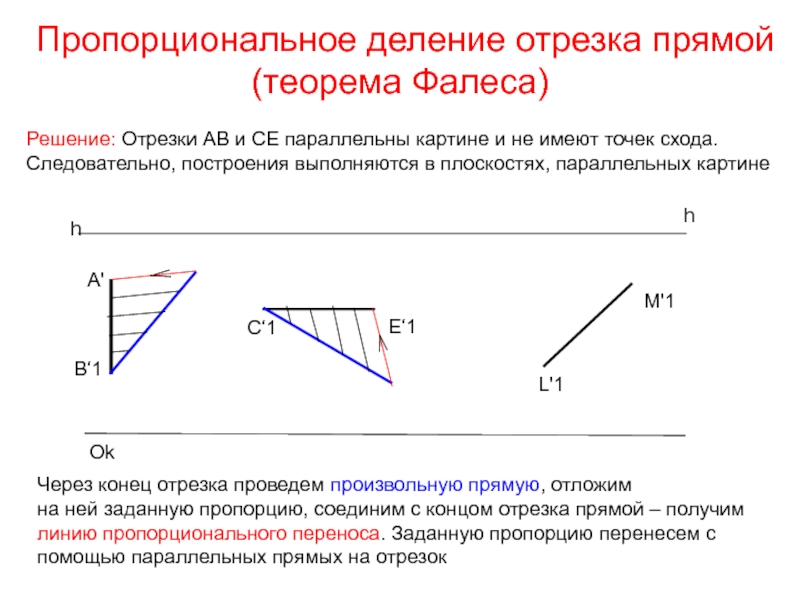
Слайд 30Пропорциональное деление отрезка прямой(теорема Фалеса)
h
h
Ok
A'
B‘1
C‘1
E‘1
L'1
M'1
Через конец отрезка проведем произвольную прямую,
отложим
на ней заданную пропорцию, соединим с концом отрезка прямой
– получим линию пропорционального переноса. Заданную пропорцию перенесем с помощью параллельных прямых на отрезок
Решение: Отрезки АВ и СЕ параллельны картине и не имеют точек схода.
Следовательно, построения выполняются в плоскостях, параллельных картине
Слайд 31Пропорциональное деление отрезка прямой(теорема Фалеса)
h
h
Ok
A'
B‘1
C‘1
E‘1
L'1
M'1
В этом случае дополнительную прямую нельзя
проводить произвольно, т.к. она также будет иметь точку схода и
пропорция будет деформироваться. Поэтому через конец отрезка проведем прямую, параллельную картине, и отложим на ней заданную пропорцию.Решение: Отрезок LM по отношению к картине расположен под углом, данная прямая имеет точку схода F. Т.к. прямая лежит на П, точка схода F находится на линии горизонта
°
F
°
°
°
°
°
Слайд 32Пропорциональное деление отрезка прямой(теорема Фалеса)
h
h
Ok
A'
B‘1
C‘1
E‘1
L'1
M'1
°
F
°
°
°
°
°
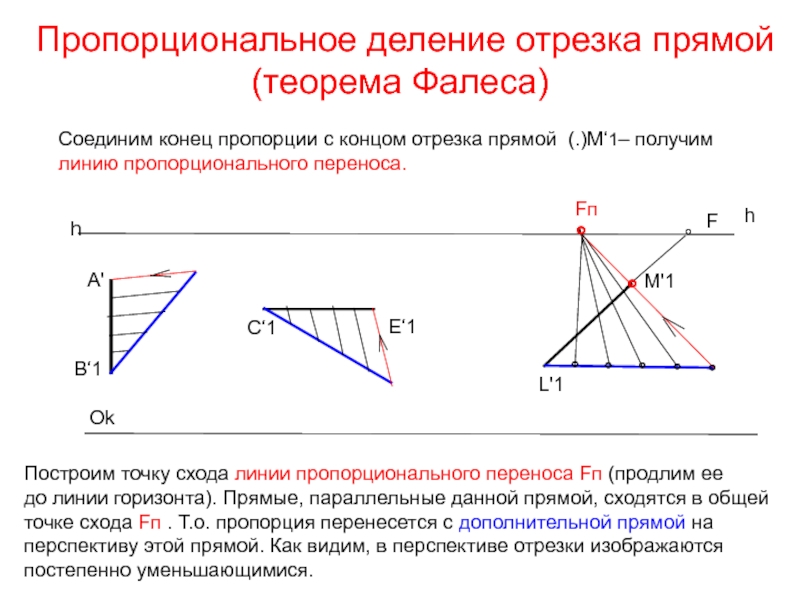
Соединим конец пропорции с концом отрезка
прямой (.)М‘1– получим
линию пропорционального переноса.
°
Fп
Построим точку схода линии
пропорционального переноса Fп (продлим ее до линии горизонта). Прямые, параллельные данной прямой, сходятся в общей точке схода Fп . Т.о. пропорция перенесется с дополнительной прямой на перспективу этой прямой. Как видим, в перспективе отрезки изображаются постепенно уменьшающимися.
°
