Слайд 1
Лекция 2.
ЭЛЕМЕНТЫ
МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
Слайд 2 ПРЕДМЕТ:
Анализ
экспериментальных данных –
значений количествен-ного признака
(артериальное давление, пульс).
Такой признак –
случайная величина.
ЗАДАЧА:
изучить законы
распределения иссле-
дуемых случайных величин,
их характеристики,
проверить ряд
гипотез,
установить, есть ли между величинами связь.
Слайд 3
Часть I.
БАЗОВЫЕ ПОНЯТИЯ
МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
Слайд 41. ПОНЯТИЯ
ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
И ВЫБОРКИ
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ – ВСЕ МНОЖЕСТВО
ОБЪЕКТОВ, ОБЛАДАЮЩИХ ДАННЫМ ПРИЗНАКОМ.
ВЫБОРКА – ЧАСТЬ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ.
ЭЛЕМЕНТЫ ВЫБОРКИ
– значения изучаемого признака у входящих в выборку объектов.
ОБЪЕМ ВЫБОРКИ N – число элементов в ней.
ВАРИАНТЫ – отличающиеся друг от друга, различные элементы выборки.
Слайд 5РЕПРЕЗЕНТАТИВНАЯ ВЫБОРКА
Чтобы по выборке можно было судить о генеральной совокупности,
выборка должна быть РЕПРЕЗЕНТАТИВНОЙ.
РЕПРЕЗЕНТАТИВНОЙ называется выборка,
верно отражающая основные законо-
мерности
генеральной совокупности.
Условия репрезентативности:
случайный отбор
достаточно большой объем
Слайд 62. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ВЫБОРКИ
ПРОСТОЙ СТАТИСТИЧЕСКИЙ РЯД
РАНЖИРОВАННЫЙ РЯД
ВАРИАЦИОННЫЙ РЯД
ИНТЕРВАЛЬНЫЙ РЯД
ПРОСТОЙ
СТАТИСТИЧЕСКИЙ РЯД –
ПЕРЕЧИСЛЕНИЕ ЭЛЕМЕНТОВ ВЫБОРКИ
В ПОРЯДКЕ ИХ ПОЛУЧЕНИЯ.
Слайд 7ПОСТРОЕНИЕ РАНЖИРОВАННОГО И ВАРИАЦИОННОГО РЯДОВ
РАНЖИРОВАННЫЙ
РЯД –
ПЕРЕЧИСЛЕНИЕ ЭЛЕМЕНТОВ ВЫБОРКИ В
ПОРЯДКЕ ИХ ВОЗРАСТАНИЯ (ИЛИ УБЫВАНИЯ).
При этом каждое значение повторяется столько
раз, сколько оно встречается в выборке.
Число появлений
данного значения, т.е. варианты, в выборке
называется частотой этой варианты, n.
Отношение частоты
к объему выборки
называется
относительной
частотой варианты,
W = n / N.
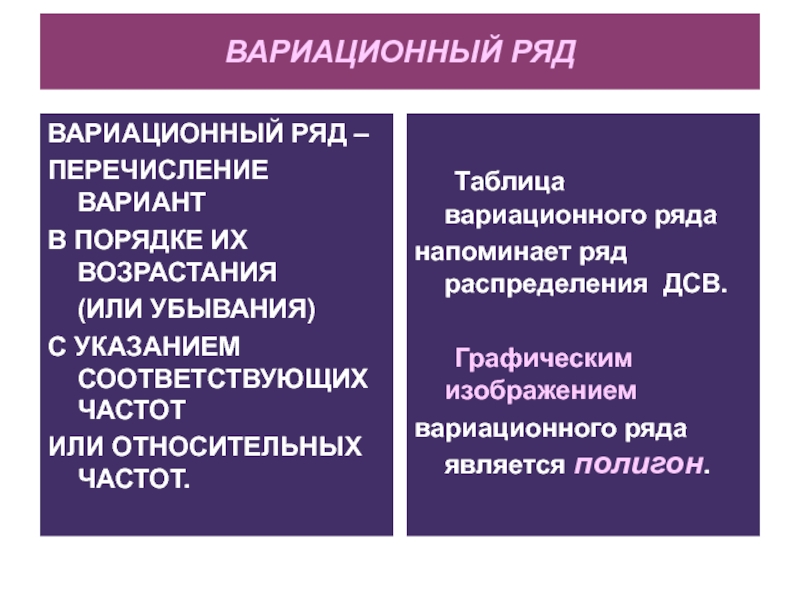
Слайд 8ВАРИАЦИОННЫЙ РЯД
ВАРИАЦИОННЫЙ РЯД –
ПЕРЕЧИСЛЕНИЕ ВАРИАНТ
В ПОРЯДКЕ ИХ ВОЗРАСТАНИЯ
(ИЛИ УБЫВАНИЯ)
С УКАЗАНИЕМ СООТВЕТСТВУЮЩИХ ЧАСТОТ
ИЛИ ОТНОСИТЕЛЬНЫХ ЧАСТОТ.
Таблица
вариационного ряда
напоминает ряд распределения ДСВ.
Графическим изображением
вариационного ряда является полигон.
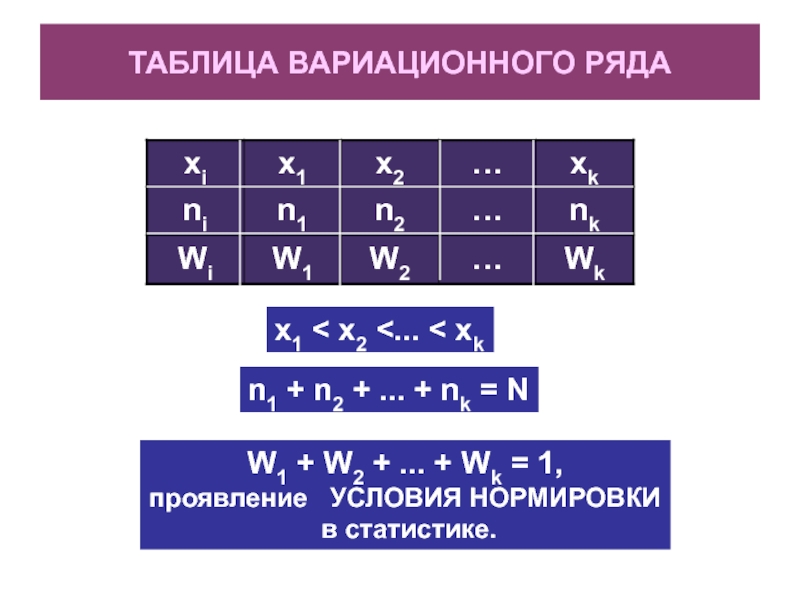
Слайд 9ТАБЛИЦА ВАРИАЦИОННОГО РЯДА
x1 < x2
+ ... + nk = N
W1 + W2 + ...
+ Wk = 1,
проявление УСЛОВИЯ НОРМИРОВКИ
в статистике.
Слайд 10
ПОЛИГОН ЧАСТОТ
или ОТНОСИТЕЛЬНЫХ ЧАСТОТ
На оси абсцисс - значения xi ,
на оси ординат - частоты ni или относительные частоты Wi.
Точки с координатами (xi, ni) соединяются отрезками прямых.
Полученная ломаная – полигон.
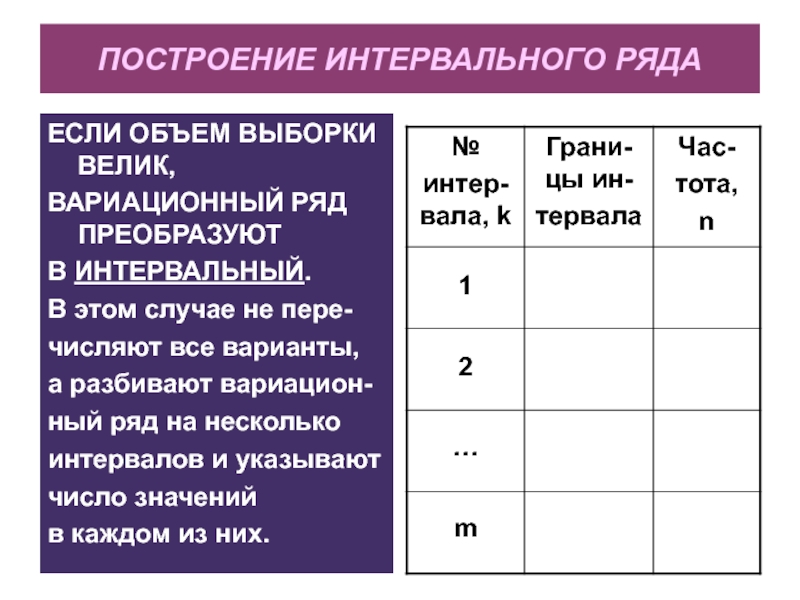
Слайд 11ПОСТРОЕНИЕ ИНТЕРВАЛЬНОГО РЯДА
ЕСЛИ ОБЪЕМ ВЫБОРКИ ВЕЛИК,
ВАРИАЦИОННЫЙ РЯД ПРЕОБРАЗУЮТ
В
ИНТЕРВАЛЬНЫЙ.
В этом случае не пере-
числяют все варианты,
а разбивают вариацион-
ный ряд
на несколько
интервалов и указывают
число значений
в каждом из них.
Слайд 12Алгоритм построения интервального ряда
Определение
разумного числа интервалов:
m =
log2N,
округляем до целого числа.
2. Размах распределения:
L = xmax - xmin.
3. Шаг разбиения, или ширина интервала:
h = ∆x = L / m =
xmax - xmin
=
m
Слайд 134. Границы интервалов:
получаются добавлением шага
к предыдущей границе.
Граница
может входить только в один интер-
вал, предыдущий или последующий.
[
- граница включа-ется в данный интервал;
( - граница не вклю-чается в интервал.
5. Подсчет частоты n - числа значений, попавших в данный интервал,
и относительной частоты
W = n / N.
Слайд 14ГИСТОГРАММА
Графическое изображение
интервального ряда –
ГИСТОГРАММА:
фигура, состоящая из прямоугольников.
Основание
каждого
прямоугольника - соответствующий интервал,
высота равна частоте или относительной частоте.
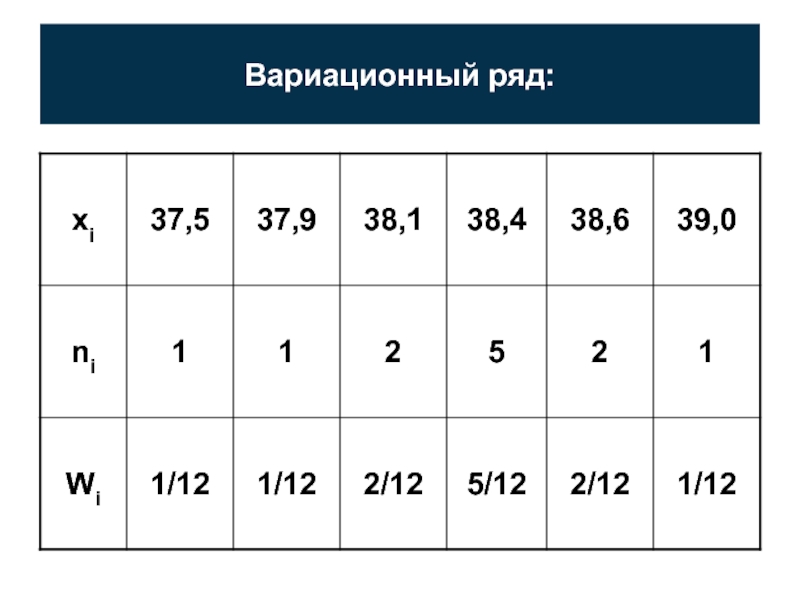
Пример.
У 12 больных гриппом,
прошедших предварительно
вакцинацию,
замерили температуру
в первые сутки болезни.
Получены значения – простой статистический ряд:
Слайд 15
37,5; 39,0; 38,1; 38,4; 37,9; 38,4;
38,4; 38,1; 38,6; 38,4; 38,6;
38,4.
Ранжированный ряд:
37,5; 37,9; 38,1; 38,1; 38,4; 38,4; 38,4; 38,4; 38,4; 38,6; 38,6; 39,0.
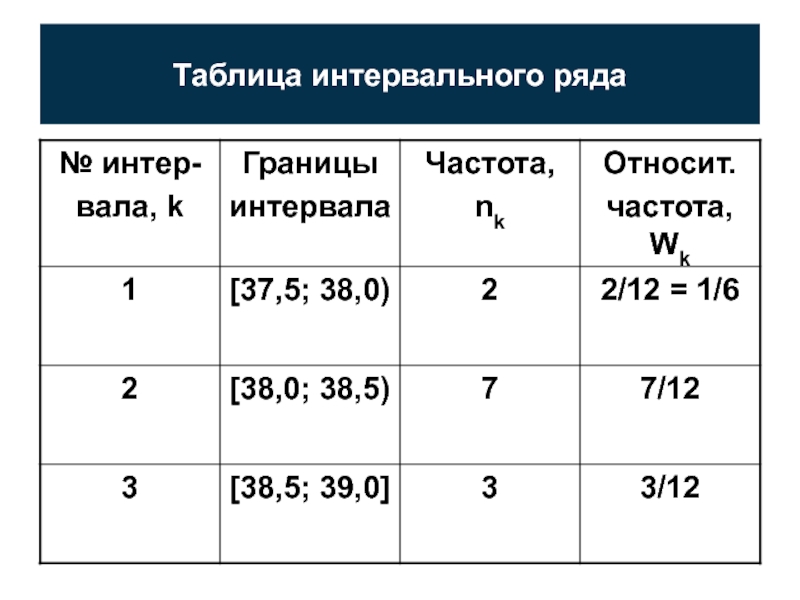
Слайд 17ИНТЕРВАЛЬНЫЙ РЯД:
m = log212 ≈ 3;
L = 39,0 -
37,5 = 1,5;
Δx = 1,5 / 3 = 0,5.
Определяем границы
первого интервала:
левая граница – x min = 37,5,
правая граница - xmin + 0,5 = 38,0.
Левую границу включаем в первый интервал, правую – нет.
С нее начнется второй интервал.
Слайд 193. ХАРАКТЕРИСТИКИ ВЫБОРКИ
Средняя выборочная х
Выборочная дисперсия
Dв =
σ2в
Выборочное средне-квадратическое отклонение σв
Мода Мо
Медиана Ме
СРЕДНЯЯ
ВЫБОРОЧНАЯ
вариационного ряда:
Σ xi ni
x =
N
Если все ni =1, то
Σ xi
x =
N
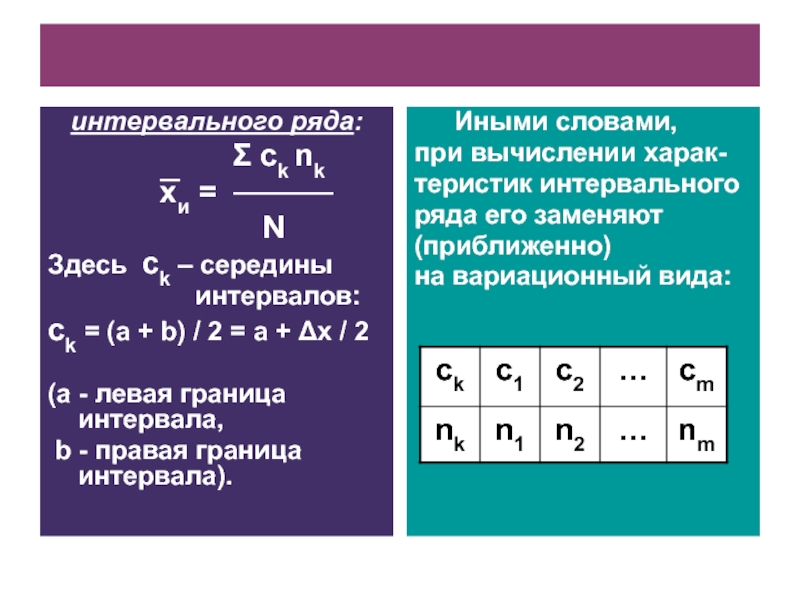
Слайд 20интервального ряда:
Σ сk nk
xи =
N
Здесь сk – середины
интервалов:
ck = (a + b) / 2 = a + Δx / 2
(a - левая граница интервала,
b - правая граница интервала).
Иными словами,
при вычислении харак-
теристик интервального
ряда его заменяют
(приближенно)
на вариационный вида:
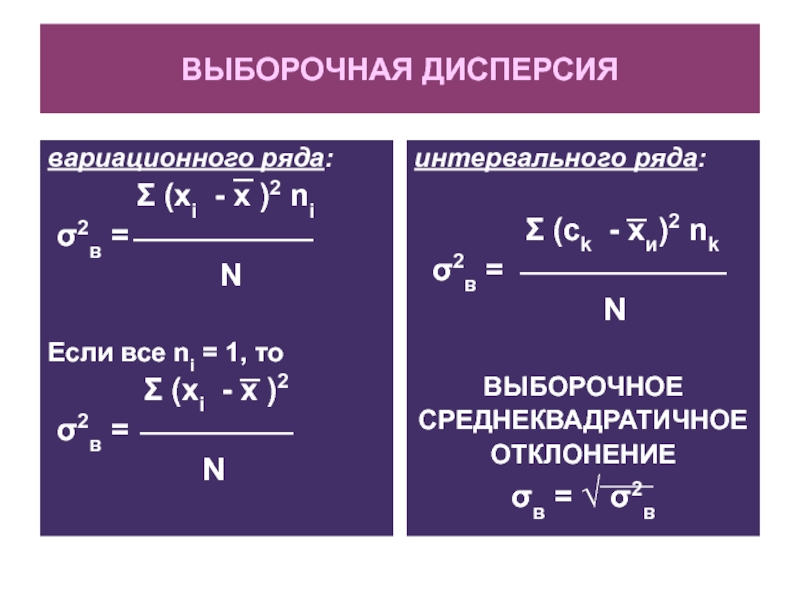
Слайд 21ВЫБОРОЧНАЯ ДИСПЕРСИЯ
вариационного ряда:
Σ (xi
- x )2 ni
σ2в =
N
Если все ni = 1, то
Σ (xi - x )2
σ2в =
N
интервального ряда:
Σ (ck - xи)2 nk
σ2в =
N
ВЫБОРОЧНОЕ
СРЕДНЕКВАДРАТИЧНОЕ
ОТКЛОНЕНИЕ
σв = √ σ2в
Слайд 22МОДА, МЕДИАНА
МОДА –
варианта с наибольшей частотой.
МЕДИАНА
делит вариационный ряд пополам:
слева от нее столько же вариант,
сколько справа.
В случае четного числа вариант медиана
равна среднему
арифметическому
двух центральных.
Определяется легко по ранжированному ряду.
В нашем примере
Mo = Me = 38,4.
Слайд 234. ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
ПО ПАРАМЕТРАМ ВЫБОРКИ
ПАРАМЕТРЫ ГЕНЕРАЛЬНОЙ
СОВОКУПНОСТИ –
числовые
характеристики
исследуемой СВ:
математическое ожидание (средняя генеральная, средняя
теоретическая) μ
дисперсия σ2
среднеквадратическое отклонение σ
ИХ ТОЧЕЧНЫЕ ОЦЕНКИ -
НАИБОЛЕЕ БЛИЗКИЕ
К НИМ (согласно теории)
ПАРАМЕТРЫ ВЫБОРКИ.
А именно:
точечная оценка
средней теоретической – средняя выборочная,
μ ≈ х
Слайд 24Точечные оценки
генеральной дисперсии – исправленная дисперсия, s2:
σ2 ≈ s2
среднеквадратичного отклонения
– стандартное отклонение, s:
σ ≈ s
Чтобы «исправить»
выборочные дисперсию
и среднеквадратическое
отклонение, нужно
ввести поправочный коэффициент:
N
s2 = σ2в∙
N-1
Σ (xi - x )2 ni
s2 =
N – 1
Σ (ck - xи)2 nk
s2и =
N – 1
Далее s = √s2
Обратите внимание:
точечные оценки –
приблизительные
и
случайные
(так как выборка сделана
из генеральной совокуп-
ности случайным образом, то ее элементы и параметры
можно считать
случайными величинами)
Слайд 265. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Дать ИНТЕРВАЛЬНУЮ ОЦЕНКУ
того или
иного пара-
метра генеральной совокупности –
значит указать
случайный интервал,
который с
заданной
вероятностью γ
(гамма) содержит
данный параметр.
Этот интервал называется
ДОВЕРИТЕЛЬНЫМ,
а γ –
ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТЬЮ,
или НАДЕЖНОСТЬЮ.
Слайд 27 Наряду с доверительной вероятностью
используют также понятие
УРОВЕНЬ ЗНАЧИМОСТИ
β = 1
– γ,
т.е. вероятность того,
что доверительный интервал НЕ содержит в себе
оцениваемый параметр.
Слайд 28Доверительный интервал
для средней теоретической
нормально распределенной величины
Имеет вид
( х
– Δ , х + Δ).
Здесь Δ – абсолютная погрешность
интервальной оценки μ
по средней выборочной
х.
Но называть ее принято
ТОЧНОСТЬЮ оценки.
В данном случае надежность
γ = P(x – Δ < μ < х + Δ)
- вероятность того, что
доверительный интервал будет содержать в себе
среднюю теоретическую.
Слайд 29
Доверительную вероятность задаем сами,
обычно в медицине это 95%,
то
есть γ = 0,95.
Точность Δ рассчитывается по формуле:
ts
Δ =
√ N
Среднюю выборочную и
стандартное отклонение
находим по выборке.
Слайд 30 t определяется
по надежности с помощью известной формулы
теории вероятности:
γ = 2Ф (t) – 1.
Отсюда
2Ф (t) = 1+
γ,
1+ γ
Ф (t) =
2
Зная Ф (t),
по таблицам нормального распределения
находим t.
Так,
если γ = 0,95, то
Ф (t) = 0,975
и t ≈ 2.
Слайд 31 Если объем выборки невелик, то вместо
таблицы нормального распределения нужно
воспользоваться
таблицей
РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА.
Значение t в таблице этого распределения находят по
заданным N и γ.
Запишем
АЛГОРИТМ
построения
доверительного
интервала
для средней
теоретической
нормально
распределенной
величины.
Слайд 32Вычислить x и s.
По заданной γ рассчитать Ф (t).
По значению
Ф (t) в таблице найти значение t.
Рассчитать точность Δ оценки
μ по х.
5. Записать ответ в виде:
х - Δ < μ < х + Δ.
Возможна краткая запись
μ = x ± Δ
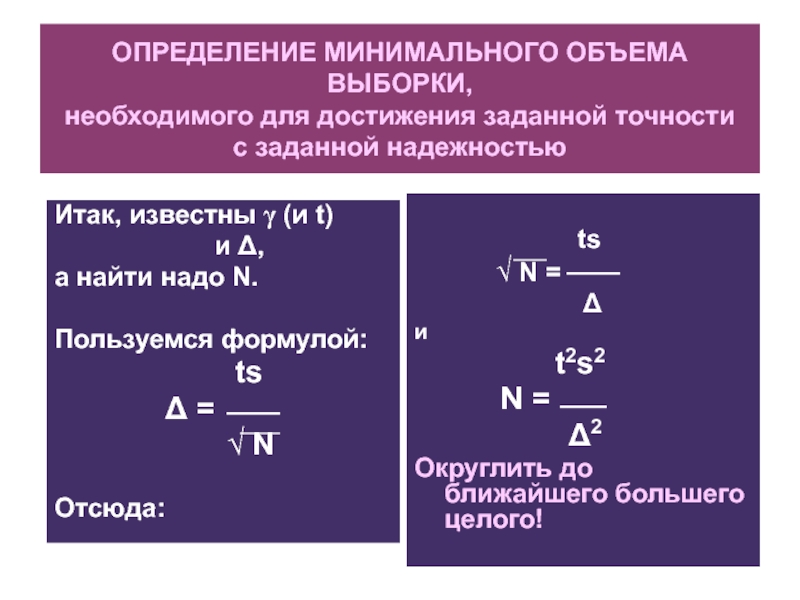
Слайд 33ОПРЕДЕЛЕНИЕ МИНИМАЛЬНОГО ОБЪЕМА ВЫБОРКИ,
необходимого для достижения заданной точности
с заданной
надежностью
Итак, известны γ (и t)
и Δ,
а найти надо
N.
Пользуемся формулой:
ts
Δ =
√ N
Отсюда:
ts
√ N =
Δ
и
t2s2
N =
Δ2
Округлить до ближайшего большего целого!