Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 30. Скалярное поле. Поверхности и линии уровня. Градиент скалярного
Содержание
- 1. Лекция 30. Скалярное поле. Поверхности и линии уровня. Градиент скалярного
- 2. § 1. Скалярные и векторные поля.Определение. (скалярного
- 3. Пример. (скалярного поля). Если в начало координат
- 4. Определение. (векторного поля). Говорят, что в трехмерном
- 5. Пример. (поверхности уровня). Если в начало координат
- 6. Определение. (векторной линии). Пусть в трехмерном пространстве
- 7. Пример. Напряженность поля можно определить путем внесения
- 8. § 2. Производная по направлению. Ее вычисление.Пусть
- 9. Df. (производной по направлению): если существует конечный
- 10. Чтобы вычислить производную по направлению, пользуются теоремой:Th.:
- 11. где a,b,g - углы определенные в любой
- 12. здесь a1,a2,a3 - бесконечно малые функции в
- 13. Перейдем к пределу в выражении (2) приЗаметим,
- 14. Значит, в пределе, учитывая, что1, 2, 3
- 15. Что и требовалось доказать.Замечание: Производная скалярного поля
- 16. § 3. Градиент скалярного поля. Связь скалярных
- 17. Определение градиента привязано к декартовой системе координат.
- 18. Вспомним, что скалярное произведение 2-х векторов вычисляется
- 19. По этой формуле можно вычислять производную по
- 20. на произвольное направление вектора
- 21. 4. 5. Если задано скалярное поле F(u(x,y,z)),
- 22. Если имеется уравнение поверхностиu(x,y,z) = 0, это
- 23. Поток.§ 5. Задача, приводящая к понятию потока
- 24. Для этого возьмем в трехмерном пространстве поверхность
- 25. Найдем количество жидкости, которое
- 26. Если сложить объемы всех
- 27. то он и будет выражать
- 28. Для того, чтобы количественно описать
- 29. Примечание: в случае жидкости поток
- 30. то поток через эту поверхность
- 31. Второй способ вычисления потока называется
- 32. Поток через поверхность S равен Пользуясь аддитивностью интеграла
- 33. Предполагая, что поверхность S однозначно
- 34. Знаки берутся с учетом
- 35. Пример: пусть дано векторное поле
- 36. Поток через всю поверхность S:
- 37. § 7. Формула Остроградского.Пусть в трехмерном пространстве
- 38. Тогда справедлива формула Остроградского:Поверхность S замкнутая.Доказательство. Самостоятельно.Формула
- 39. § 8. Векторная запись теоремы Остроградского.
- 40. Так как S - замкнутая, гладкая, ориентированная,
- 41. Сравнивая правые части
- 42. Пример: Поток векторного поля
- 43. Замечание: из материала, приведенного выше ясно, что
- 44. § 9. Дивергенция векторного поля, ее вычисление.В
- 45. В некоторых задачах необходимо
- 46. Если поверхность S стягивать в
- 47. содержащемся внутри этой поверхности, при
- 48. Теорема. (о вычислении дивергенции)
- 49. Доказательство: По определению: Так
- 50. Значит, дивергенция поля может быть
- 51. Частные производные непрерывны, необходимо учитывать,
- 52. Скачать презентанцию
§ 1. Скалярные и векторные поля.Определение. (скалярного поля). Если в трехмерном пространстве определена функция u(x,y,z), то говорят, что задано скалярное поле u(x,y,z).Замечание. Другими словами говоря, задание скалярного поля означает, что каждой
Слайды и текст этой презентации
Слайд 2§ 1. Скалярные и векторные поля.
Определение. (скалярного поля). Если в
трехмерном пространстве определена функция u(x,y,z), то говорят, что задано скалярное
поле u(x,y,z).Замечание. Другими словами говоря, задание скалярного поля означает, что каждой точке M(x,y,z) поставлено в соответствие число, которое является значением функции u в точке M.
Слайд 3Пример. (скалярного поля). Если в начало координат поместить заряд Q,
то в каждой точке пространства определена функция
,где: - расстояние от точки до начала координат; - потенциал,
0 – диэлектрическая постоянная вакуума.
Задание функции задает скалярное поле потенциала.
Слайд 4Определение. (векторного поля). Говорят, что в трехмерном пространстве задано векторное
поле
Замечание. В этом случае каждой точке пространства M(x,y,z) ставится в
соответствие вектор в точке M(x,y,z).Для скалярных и векторных полей вводится понятие поверхностей уровня.
Определение. (поверхностей уровня). Пусть задано скалярное поле u(x,y,z). Поверхностью уровня данного скалярного поля, называется поверхность, задаваемая уравнением
u(x,y,z) = сonst.
Слайд 5Пример. (поверхности уровня). Если в начало координат поместить заряд Q,
то имеем скалярное поле потенциала
,Поверхностью уровня является поверхность:
где: с = const.
- сфера
Такие поверхности называются эквипотенциальными.
Слайд 6Определение. (векторной линии). Пусть в трехмерном пространстве задано векторное поле
Векторной
линией заданного векторного поля называется линия, в каждой точке которой
вектор касательной совпадает по направлению с вектором .Замечание. Уравнение векторных линий можно находить по формуле:
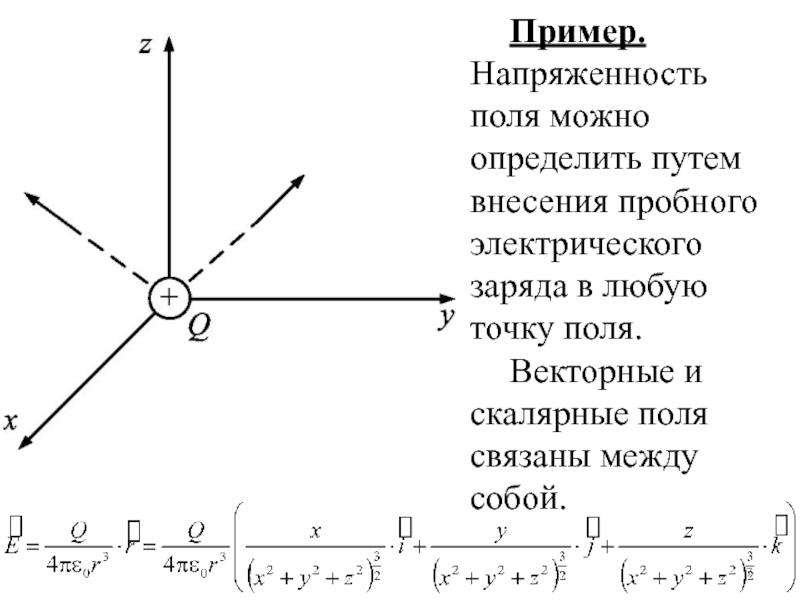
Слайд 7Пример. Напряженность поля можно определить путем внесения пробного электрического заряда
в любую точку поля.
Векторные и скалярные поля связаны между
собой.
Слайд 8§ 2. Производная по направлению.
Ее вычисление.
Пусть задано скалярное поле
u, где u – дифференцируемая функция. Возьмем в трехмерном пространстве
вектор l, расположенный в этом скалярном поле. Пустьначало вектора l характеризует
точку М0. Возьмем на векторе l
соседнюю точку М . Точка М как
и М0 находится в скалярном поле u . Поэтому имеет смысл приращение скалярного поля u в точке М0, выраженное формулой:
Слайд 9Df. (производной по направлению): если существует конечный предел отношения приращения
скалярного поля
к длине вектора,
т.е. к , то этот предел называется производной скалярного поля u по направлению l и обозначается:
Слайд 10Чтобы вычислить производную по направлению, пользуются теоремой:
Th.: (о вычислении производной
по направлению).
Если скалярное поле u(x,y,z) дифференцируемо в каждой точке некоторой
области V, то производная по направлению в каждой точке V существует и она выражается формулой: 
Слайд 11где a,b,g - углы определенные в любой точке области V
, которые составляет вектор l с координатными осями.
Док-во: т.к. скалярное
поле u дифференцируется в области V, значит, в любой окрестности точки М0 V существует приращение скалярного поля, находимого по формуле:
Слайд 12здесь a1,a2,a3 - бесконечно малые функции в точке М0 ,
которые стремятся к 0, когда
- это проекции вектора ,
совпадающего по направлению с вектором на
координатные оси.
- частные производные.
Разделим левую и правую части на длину вектора
После чего получаем:
Слайд 13Перейдем к пределу в выражении (2) при
Заметим, что
Если заменить x
на y и x на z, то в пределе получим
cos и cos.
Слайд 14Значит, в пределе, учитывая, что
1, 2, 3 0 при
,
имеем:Так как предел правой части (2) существует и выражается правой частью формулы (3), то и предел левой части формулы (3) существует. Он равен производной скалярного поля по направлению. Значит, производная скалярного поля u по направлению l выражается формулой:
Слайд 15Что и требовалось доказать.
Замечание: Производная скалярного поля по направлению вектора
выражает скорость возрастания или убывания скалярного поля по направлению
вектора , если:- поле возрастает
- поле убывает.
Вычисление скалярного поля производится по формуле (4).
Пример: на практике.
Слайд 16§ 3. Градиент скалярного поля. Связь скалярных и векторных полей.
Свойства градиента.
Определение. (градиента). Градиентом дифференцируемого скалярного поля называется вектор
.Замечание. На практике встречаются равносильные обозначения градиента:
gradu u,
где: - оператор «Набла».
Слайд 17Определение градиента привязано к декартовой системе координат. Покажем связь скалярных
и векторных полей.
Пусть задано скалярное поле u(x,y,z), дифференцируемое в некотором
V. -произвольный вектор V. По определению:
Но эта запись означает, что скалярному полю u c помощью grad поставлено в соответствие векторное поле grad. Что и говорит о том, что скалярное и векторное поле связаны между собой.
Слайд 18Вспомним, что скалярное произведение 2-х векторов вычисляется по формуле:
Найдем скалярное
произведение градиента поля u и вектора , получим:
- произвольный единичный вектор V.В правой части производная по направлению:
Слайд 19По этой формуле можно вычислять производную по направлению, зная градиент.
Учитывая,
что:
= проекцияlgradu = Df. (инвариантное определение градиента, не зависящего от системы координат).
Градиентом скалярного поля u называется вектор, обозначенный gradu, проекция которого
Слайд 20на произвольное направление вектора равна производной скалярного
поля по направлению этого вектора .
Свойства градиента:
Градиент дифференцируемого
скалярного поля u(x,y,z) перпендикулярен к поверхности уровня этого скалярного поля (совпадает с нормалью) и направлен в сторону возрастания скалярного поля.2. grad(c1u1 + c2u2) = c1gradu1 + c2gradu2,
c1, c2 = const;
u1, u2 – скалярные поля.
3. grad(u1u2) = u2gradu1 + u1gradu2.
Слайд 21
4.
5. Если задано скалярное поле F(u(x,y,z)), то градиент:
gradF(u(x,y,z)) =
Fugradu.
§ 4. Применение градиента для вычисления нормали к поверхности.
Для поля
u(x,y,z) введем понятие градиента:
Слайд 22Если имеется уравнение поверхности
u(x,y,z) = 0, это означает, что задана
поверхность уровня скалярного поля u(x,y,z).
Так как градиент скалярного поля направлен
по нормали к поверхности уровня, то единичный вектор нормали к поверхности можно найти по формуле:Пример. На практике
Слайд 23Поток.
§ 5. Задача, приводящая к понятию потока векторного поля.
Пусть в
трехмерном пространстве имеется ориентируемая поверхность S и векторное поле, задаваемое
формулой:Считаем, что векторное поле в каждой точке векторного пространства задает поле скоростей жидкости. Попробуем найти количество жидкости, которое протекает через поверхность S в направлении нормали.
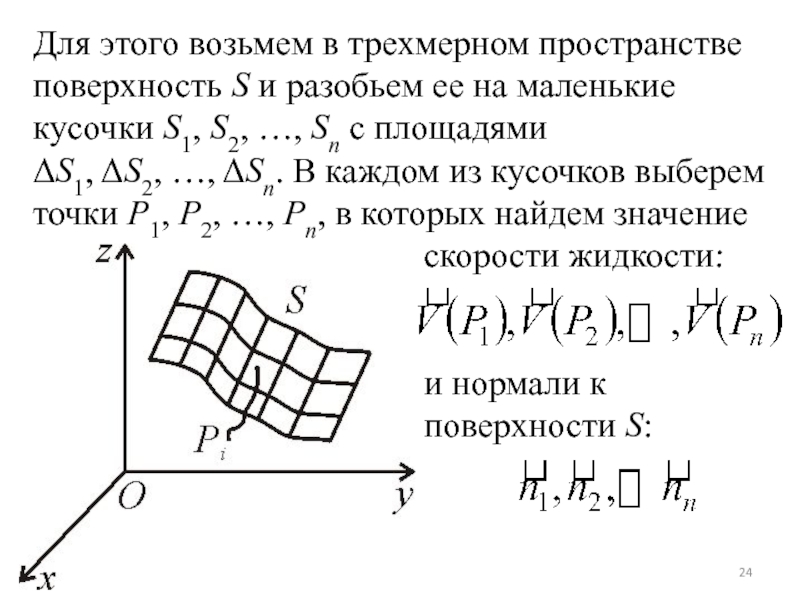
Слайд 24Для этого возьмем в трехмерном пространстве поверхность S и разобьем
ее на маленькие кусочки S1, S2, …, Sn с площадями
S1,
S2, …, Sn. В каждом из кусочков выберем точки P1, P2, …, Pn, в которых найдем значениескорости жидкости:
и нормали к
поверхности S:
Слайд 25 Найдем количество жидкости, которое протекает через участок
Si в единицу времени в направлении нормали.
Численно это
значение равно объему параллелепипеда, построенного на Si как на основании с высотой 
Слайд 26 Если сложить объемы всех маленьких параллелепипедов, то
количество жидкости, протекающее через поверхность S, обозначаемое Q равно: При
таком приближенном вычислении количество жидкости зависит от способа разбиения и выбора точек Pi.В физике величина не зависит. Считаем, если существует конечный предел
Слайд 27 то он и будет выражать значение количества жидкости,
протекающей через поверхность S. Вспоминая, если предел существует, то он
называется поверхностным интегралом 1-го рода.Количество жидкости, протекающей через поверхность S равно поверхностному интегралу 1-го рода от скалярного произведения скорости на единичный вектор нормали к поверхности.
Слайд 28 Для того, чтобы количественно описать векторы, электростатического, электромагнитного
поля вводится понятие потока.
Определение (потока).
Потоком векторного
поля
называется число, обозначаемое буквой П и вычисляемое как:
Слайд 29 Примечание: в случае жидкости поток равен количеству жидкости,
протекающей через поверхность.
§ 6. Вычисление потока.
Если задано
векторное поле ,
и задана поверхность S, нормаль к которой может быть вычислена:
Слайд 30 то поток через эту поверхность S может быть
вычислен по определению
При этом поверхность S должна быть однозначно
проектируемой на одну из координатных плоскостей. В этом случае поверхностный интеграл по поверхности S сводится к интегралу по области проектирования поверхности S
Слайд 31 Второй способ вычисления потока называется методом проектирования на
координатной плоскости. Чтобы получить формулы, заметим, что нормаль к поверхности
может быть представлена:где - углы которые составляет нормаль с координатными осями.
Тогда, в силу определения скалярного произведения, имеем:
Слайд 33 Предполагая, что поверхность S однозначно проектируется на координатные
оси имеем:
Поверхностные интегралы 2 рода вычисляются с
учетом области проектиро-вания на координатную плоскость. Для вычисления потока методом проектирования на координатные плоскости имеем 
Слайд 34 Знаки берутся с учетом того, какой угол
составляет нормаль к поверхности для 1-го интеграла с осью x,
для 2-го с осью y, для3-го с осью z.
Замечание: В том случае если поток через замкнутую поверхность > 0, то внутри замкнутой поверхности есть источник. Если поток < 0 ,то внутри поверхности находится сток.
Если поток = 0, то говорят, что количество вещества втекающего в поверхность = кол-ву вещества вытекающего из нее.
Слайд 35 Пример: пусть дано векторное поле
найти поток через внешнюю поверхность конуса
S:
составляет тупой угол с осью z.
Слайд 37§ 7. Формула Остроградского.
Пусть в трехмерном пространстве задана область V,
такая что:
Ориентированная внешней нормалью.
Имеющая кусочно-гладкую поверхность S.
В области V и
на её границе S функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими частными производными
Слайд 38Тогда справедлива формула Остроградского:
Поверхность S замкнутая.
Доказательство. Самостоятельно.
Формула Остроградского применима только
в случае замкнутых поверхностей.
Если поверхность S ориентирована внешней нормалью, в
формуле берется знак «+», если внутренней «-» перед поверхностным интегралом.
Слайд 39 § 8. Векторная запись теоремы Остроградского.
Пусть в 3-х мерном пространстве задано векторное поле
где
P, Q, R интегрируемы вместе со своими производными.Пусть в пространстве задана замкнутая гладкая поверхность, ориентируемая внешней нормалью .
Слайд 40Так как S - замкнутая, гладкая, ориентированная, а функции P,
Q, R удовлетворяют условиям теоремы Остроградского, имеем:
Поток через поверхность
S можно
вычислить по формуле: 
Слайд 41
Сравнивая правые части формул (1) и
(2) и
вспоминая что
имеем:
- векторная запись теоремы
Остроградского.Поток векторного поля через замкнутую поверхность = по объему от этой поверхности, от дивергенции векторного поля.
Слайд 42Пример:
Поток векторного поля через поверхность
неизвестен.
S:
нормаль внешняя
S - замкнутая поверхность – это боковые поверхности конуса и плоскость z = 2.Найдем заранее:
Слайд 43Замечание: из материала, приведенного выше ясно, что скалярным полям можно
поставить в соответствие векторные поля, а векторным- скалярные. Если дано
скалярное поле U(x,y,z) то с помощью операций gradU скалярному полю можно ставить в соответствие векторное поле. Если есть векторное поле , то с помощью div можно поставить в соответствие векторному полю скалярное поле.
Слайд 44§ 9. Дивергенция векторного поля, ее вычисление.
В векторном поле
возьмем замкнутую поверхность S с внешней нормалью .
Можем получить характеристику поля, называемую потоком, воспользовавшись формулой:Если взять поверхность S1, то поток будет другим, чем через поверхность S, и понятие потока отражает количественную характеристику векторного поля при наличии некоторой поверхности, и зависит не только от векторного поля но и от поверхности.
Слайд 45
В некоторых задачах необходимо знать характеристики
векторного поля в каждой точке, независимо от выбора поверхности S.
Если разделить поток на объем поверхности:-
средняя плотность потока через поверхность S.
Слайд 46 Если поверхность S стягивать в точку и предполагать
что существует предел такого отношения, то получим плотность потока в
точке.Эту характеристику по определению называют дивергенцией векторного поля.
Определение. (дивергенции) Если существует конечный предел отношения потока векторного поля через замкнутую поверхность S к V,
Слайд 47 содержащемся внутри этой поверхности, при стягивании поверхности S
в точку, этот предел называется дивергенцией векторного поля в точке
и обозначается: Физический смысл дивергенции - плотность потока векторного поля.Если div > 0, то в точке - источник,
если < 0, то сток,
если = 0, то ничего не находится
Слайд 48 Теорема. (о вычислении дивергенции)
Если в 3-х
мерном пространстве задано
векторное поле
где P, Q,
R непрерывны вместе со своими производнымив некоторой области V, то в каждой точке этой области дивергенция может быть вычислена по формуле
Слайд 49Доказательство:
По определению:
Так как поверхность S замкнутая,
то применяя формулу Остроградского имеем:
Слайд 50 Значит, дивергенция поля может быть записана
Частные
производные непрерывны, значит к тройному интегралу применима теорема о среднем.
Слайд 51 Частные производные непрерывны, необходимо учитывать, что поверхность S
стягивается в точку M, можно записать, что
и перейти к пределу под знаком непрерывной функции, после чего получим:
