Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4
Содержание
- 1. Лекция 4
- 2. Оценка ценных бумагРазличия концепций оценки стоимостиОценка облигацийОценка привилегированных акцийОценка обыкновенных акцийСтавки дохода ( Yields)
- 3. Что такое стоимость?Коммерческая стоимость (Going-concern value) –
- 4. Что такое стоимость?(2) фирмы: стоимость суммарных активов
- 5. Что такое стоимость?Действительная (внутренняя)(Intrinsic value) цена, которую
- 6. Облигации-характеристикиНоминальная стоимость (maturity value (MV) [or face
- 7. Облигации-характеристикиСтавка дисконтирования или капитализации(discount rate, capitalization rate)
- 8. Различные типы облигацийБессрочные облигации (perpetual bond)- облигации,
- 9. Пример бессрочной облигацииОблигация P имеет $1,000 номинальную
- 10. Пример бессрочной облигацииОблигация P приносит $50 годовой
- 11. Пример купонной облигацииКупонная облигация(non-zero coupon-paying bond) –
- 12. Облигация C имеет $1,000 номинальную стоимость
- 13. Бескупонная облигация Бескупонная облигация (zero coupon bond)-
- 14. V = $1,000 (PVIF10%, 30)
- 15. Начисление процентов раз в полгода (1) Разделить kd
- 16. (1 + kd/2 ) 2*n(1 + kd/2
- 17. V = $40 (PVIFA5%, 30) + $1,000 (PVIF5%,
- 18. Пример купонной облигацииКакой процент от номинала?Какова стоимость?
- 19. АКЦИИ
- 20. Привилегированная акция (Preferred Stock) – Тип акций,
- 21. Оценка привилегированных акцийЭто снижение до бесконечности!(1 +
- 22. Пример привилегированной акции DivP = $100 (
- 23. Оценка обыкновенной акцииПропорциональная доля в будущих доходах
- 24. Оценка обыкновенной акции (1) Будущие дивиденды (2)
- 25. Модель оценки дивидендовМодель оценки дивидендов основывается на
- 26. Модель оценки с учетом факта будущей продажи
- 27. Модели учитывают прогнозы по всем будущим дивидендам.
- 28. Модель постоянного ростаМодель постоянного роста предусматривает, что
- 29. Пример модели постоянного ростаАкция CG имеет размер
- 30. Модель нулевого ростаМодель нулевого роста предполагает, что
- 31. Пример модели нулевого ростаАкция ZG имеет ожидаемую
- 32. D0(1+g1)tDn(1+g2)tМодель роста по фазамМодель роста по фазам
- 33. Вычисление рыночной ставки доходности1. Определить ожидаемый денежный
- 34. Определение доходности при погашении облигацииДоходность при погашении
- 35. Определение доходности (YTM)Вы хотите определить доходность(YTM) по
- 36. Решение (пробуем 9%)$1,250 = $100(PVIFA9%,15) +
- 37. Решение (пробуем 7%)$1,250 = $100(PVIFA7%,15) +
- 38. .07 $1,273 .02 IRR $1,250 $192 .09 $1,081 X $23 .02 $192Решение (Интерполяция)$23X=
- 39. .07 $1,273 .02 IRR $1,250 $192 .09 $1,081 X $23 .02 $192Решение (Интерполяция)$23X=
- 40. .07 $1273 .02 YTM $1250 $192 .09 $1081 ($23)(0.02) $192 Решение (интерполяция)$23XX
- 41. Определение доходности облигации с полугодовым купоном P0
- 42. Определение YTM по облигации с полугодовым купономВы
- 43. Определение YTM по облигации с полугодовым купоном[
- 44. Соотношение стоимости и доходности облигацииДисконт по облигации
- 45. Соотношение стоимости и доходности облигации Ставка
- 46. Соотношение стоимости и доходности облигацийДопустим, что требуемая
- 47. Соотношение стоимости и доходности по облигации
- 48. Соотношение цены и доходности при растущих ставкахТаким
- 49. Соотношение цены и доходностиДопустим, что требуемая ставка
- 50. Соотношение цены и доходности Ставка по
- 51. Соотношение цены и доходности при снижении ставок
- 52. Роль срока до погашенияДопустим, что требуемая ставка
- 53. Соотношение цены и доходности Ставка по
- 54. Роль срока облигации5 –летний бонд вырос в
- 55. Определение доходности по привилегированным акциямОпределение доходности по
- 56. Пример определения доходности по привилегированной акцииkP =
- 57. Определение доходности по обыкновенной акцииПрименима модель постоянного
- 58. Пример доходности обыкновенной акцииke = ( $3
- 59. источникиОсновы финансового менеджмента12-е изданиеДжеймс К. Ван ХорнСтанфордский
- 60. Скачать презентанцию
Оценка ценных бумагРазличия концепций оценки стоимостиОценка облигацийОценка привилегированных акцийОценка обыкновенных акцийСтавки дохода ( Yields)
Слайды и текст этой презентации
Слайд 2Оценка ценных бумаг
Различия концепций оценки стоимости
Оценка облигаций
Оценка привилегированных акций
Оценка обыкновенных
акций
Слайд 3Что такое стоимость?
Коммерческая стоимость (Going-concern value) – стоимость, по которой
фирма может быть продана как реально функционирующий бизнес.
Ликвидационная стоимость (Liquidation
value) – стоимость, по которой данный актив или группа активов (например, фирма) могут быть проданы отдельно от операционной компании.
Слайд 4Что такое стоимость?
(2) фирмы: стоимость суммарных активов фирмы минус обязательства
и стоимость привилегированных акций
Балансовая стоимость (Book value)
(1) актива: Стоимость
актива по данным бухгалтерского баланса т.е. его первоначальная стоимость минус накопленный износ; 
Слайд 5Что такое стоимость?
Действительная (внутренняя)(Intrinsic value) цена, которую ценная бумага «должна
иметь» с учетом всех факторов влияющих на ее оценку.
Рыночная стоимость
(Market value) – рыночная цена, по которой актив торгуется.
Слайд 6Облигации-характеристики
Номинальная стоимость (maturity value (MV) [or face value] – установленная
эмитентом стоимость. В США номинальная стоимость облигации обычно $1,000.
Облигация(
bond ) - долгосрочный долговой инструмент, эмитированный правительством или корпорацией.![Облигации-характеристикиНоминальная стоимость (maturity value (MV) [or face value] – установленная эмитентом стоимость. В США номинальная стоимость облигации](/img/tmb/7/644411/2098022073f1cec50469ebde063b09dd-800x.jpg "Лекция 4 Облигации-характеристикиНоминальная стоимость (maturity value (MV) [or face value] – установленная эмитентом")
Слайд 7Облигации-характеристики
Ставка дисконтирования или капитализации(discount rate, capitalization rate) зависит от риска
по облигации и состоит из ставки по безрисковым бумагам, плюс
премия за риск.Купонная ставка (coupon rate) установленная эмитентом процентная ставка; годовой доход по облигации деленный на номинальную стоимость.
Слайд 8Различные типы облигаций
Бессрочные облигации (perpetual bond)- облигации, которые не имеют
определенного срока погашения. Бессрочная рента в форме облигации.
(1 + kd)1
(1
+ kd)2(1 + kd)¥
V =
+
+ ... +
I
I
I
= S
t=1
(1 + kd)t
I
или I (PVIFA kd, ¥ )
V = I / kd
¥
Слайд 9Пример бессрочной облигации
Облигация P имеет $1,000 номинальную стоимость и приносит
8% годовой купон. Применяемая ставка дисконтирования 10%. Какова стоимость бессрочной
облигации?
I = $1,000 ( 8%) = $80.
kd = 10%.
V = I / kd [В сокращении]
= $80 / 10% = $800. Если цена выше, то мы отказываемся от инвестирования
Слайд 10Пример бессрочной облигации
Облигация P приносит $50 годовой купон. Применяемая ставка
дисконтирования 12%. Какова стоимость бессрочной облигации?
I
= $50.kd = 12%.
V = I / kd [В сокращении]
= $50 / 12% = $417.67 Если цена выше, то мы отказываемся от инвестирования
Слайд 11Пример купонной облигации
Купонная облигация(non-zero coupon-paying bond) – с выплатой купонного
дохода и с конечным сроком погашения.
(1 + kd)1
(1 + kd)2
(1
+ kd)nV =
+
+ ... +
I
I + MV
I
= S
n
t=1
(1 + kd)t
I
V = I (PVIFA kd, n) + MV (PVIF kd, n)
(1 + kd)n
+
MV
Слайд 12Облигация C имеет $1,000 номинальную стоимость и 8% годовой
купон на 30 лет. Ставка дисконтирования равна 10%. Какова стоимость
облигации?Пример купонной облигации
V = $80 (PVIFA10%, 30) + $1,000 (PVIF10%, 30) = $80 (9.427) + $1,000 (.057)
[таблица 4] [таблица 2]
= $754.16 + $57.00 = $811.16.
Слайд 13Бескупонная облигация
Бескупонная облигация (zero coupon bond)- по ней не
выплачивается процентов, но она продается со значительной скидкой от номинала;
инвесторы получают выгоду за счет роста ее рыночной цены(1 + kd)n
V =
MV
= MV (PVIFkd, n)
Слайд 14 V = $1,000 (PVIF10%, 30) = $1,000 (.057)
= $57.00
Пример бескупонной облигации
Облигация Z имеет $1,000
номинальную стоимость и срок 30 лет. Ставка дисконтирования 10%. Определите стоимость бескупонной облигации.
Слайд 15Начисление процентов раз в полгода
(1) Разделить kd на 2
(2) Умножить
n на 2
(3) Разделить I на 2
Большинство облигаций в США
платят проценты 2 раза в год (1/2 от годового купона).Необходимые исправления:
Слайд 16(1 + kd/2 ) 2*n
(1 + kd/2 )1
Начисление процентов раз
в полгода
Купонная облигация non-zero coupon bond с начислением процентов раз
в полгода.V =
+
+ ... +
I / 2
I / 2 + MV
= S
2*n
t=1
(1 + kd /2 )t
I / 2
= I/2 (PVIFAkd /2 ,2*n) + MV (PVIFkd /2 ,2*n)
(1 + kd /2 ) 2*n
+
MV
I / 2
(1 + kd/2 )2
Слайд 17V = $40 (PVIFA5%, 30) + $1,000 (PVIF5%, 30)
= $40
(15.373) + $1,000 (.231)
Таблица IV
Таблица II= $614.92 + $231.00 = $845.92
Пример купонной облигации
Облигация C имеет $1,000 номинал и 8% полугодовой купон. Срок 15 лет. Требуемая ставка доходности (discount rate) 10% (годовая ставка). Определите стоимость облигации
Слайд 18Пример купонной облигации
Какой процент от номинала?
Какова стоимость?
84.628% от номинала
(курс, как пишут в финансовых сводках)
84.628% x $1,000 (номинал) =
$846.28
Слайд 20Привилегированная акция (Preferred Stock) – Тип акций, по которому, как
правило, предусмотрена выплата фиксированных дивидендов (по усмотрению совета директоров компании).
Оценка привилегированных акций
Привилегированные акции обладают преимуществами по сравнению с обыкновенными акциями относительно выплаты дивидендов и предъявления требований на активы.
Слайд 21Оценка привилегированных акций
Это снижение до бесконечности!
(1 + kP)1
(1 + kP)2
(1
+ kP)¥
V =
+
+ ... +
DivP
DivP
DivP
= S
t=1
(1 + kP)t
DivP
или DivP(PVIFA kP,
¥ )V = DivP / kP
¥
Слайд 22Пример привилегированной акции
DivP = $100 ( 8% ) =
$8.00.
kP = 10%. V = DivP / kP
= $8.00 / 10% = $80Акция PS имеет 8% размер дивидендов, номинальную стоимость $100 . Ставка дисконтирования (discount rate) 10%. Определите цену привилегированной акции
Слайд 23Оценка обыкновенной акции
Пропорциональная доля в будущих доходах после всех других
обязательств фирмы (если останутся).
Дивиденды могут быть выплачены пропорционально доле в
доходах.Обыкновенные акции (Common stock) - Ценные бумаги, которые предоставляют инвестору права на определенную долю собственности (и риска) в корпорации.
Слайд 24Оценка обыкновенной акции
(1) Будущие дивиденды
(2) Будущая продажа акций
Какой
денежный поток получит акционер от владения обыкновенными акциями?
Слайд 25Модель оценки дивидендов
Модель оценки дивидендов основывается на PV от стоимости
всех будущих дивидендов.
(1 + ke)1
(1 + ke)2
(1 + ke)¥
V =
+
+
... +Div1
Div¥
Div2
= S
t=1
(1 + ke)t
Divt
Divt: Размер дивиденда во время t
ke: Требуемая инвестором ставка
¥
Слайд 26Модель оценки с учетом факта будущей продажи акции.
(1 + ke)1
(1
+ ke)2
(1 + ke)n
V =
+
+ ... +
Div1
Divn + Ценаn
Div2
n: Год в
котором акции планируются к продаже.Цена n : Ожидаемая стоимость акции в год n.
Модель оценки дивидендов на определенный срок
Слайд 27Модели учитывают прогнозы по всем будущим дивидендам. Следующие допущения в
изменении роста дивидендов возможны:
Постоянный рост
Нет роста
Рост по фазам
Допускаемые модели роста
дивидендов
Слайд 28Модель постоянного роста
Модель постоянного роста предусматривает, что дивиденды будут расти
вечно на ставку g.
(1 + ke)1
(1 + ke)2
(1 + ke)¥
V
=+
+ ... +
D0(1+g)
D0(1+g)¥
=
(ke - g)
D1
D1: Дивиденд в период 1.
g : Постоянная ставка роста.
ke: Требуемая доходность.
D0(1+g)2
Слайд 29Пример модели постоянного роста
Акция CG имеет размер роста дивиденда в
год в 8%. По каждой акции получен годовой дивиденд $3.24
. Ставка дисконтирования - 15%. Какова стоимость обыкновенной акции?D1 = $3.24 ( 1 + .08 ) = $3.50
VCG = D1 / ( ke - g ) = $3.50 / ( .15 - .08 ) = $50
Слайд 30Модель нулевого роста
Модель нулевого роста предполагает, что дивиденды будут расти
вечно на ставку g = 0.
(1 + ke)1
(1 + ke)2
(1
+ ke)¥VZG =
+
+ ... +
D1
D¥
=
ke
D1
D1: Дивиденд в период 1.
ke: Требуемая доходность.
D2
Слайд 31Пример модели нулевого роста
Акция ZG имеет ожидаемую ставку роста дивидендов
в 0%. Каждая акция получила годовой дивиденд в размере $3.24.
Ставка дисконтирования 15%. Определите стоимость обыкновенной акции.D1 = $3.24 ( 1 + 0 ) = $3.24
VZG = D1 / ( ke - 0 ) = $3.24 / ( .15 - 0 ) = $21.60
Слайд 32D0(1+g1)t
Dn(1+g2)t
Модель роста по фазам
Модель роста по фазам предполагает, что дивиденды
по каждой акции будут расти по двум или более процентным
ставкам.(1 + ke)t
(1 + ke)t
V =S
t=1
n
S
t=n+1
¥
+
Слайд 33Вычисление рыночной ставки доходности
1. Определить ожидаемый денежный поток.
2. Заменить внутреннюю
стоимость (V) на рыночную(P0).
3. Определить рыночную ставку доходности, которая приравнивает
дисконтированную стоимость ожидаемых денежных поступлений к текущей рыночной цене соответствующей ценной бумаги и которую называют также рыночной доходностью (yield), Шаги для подсчета ставки доходности:
Слайд 34Определение доходности при погашении облигации
Доходность при погашении - ожидаемая доходность
облигации, которая была куплена по текущему рыночному курсу и хранится
до наступления срока ее погашения,Определить доходность (YTM) облигации с годовым купоном и ограниченным сроком действия.
P0 =
S
n
t=1
(1 + kd )t
I
= I (PVIFA kd , n) + MV (PVIF kd , n)
(1 + kd )n
+
MV
kd = YTM
Слайд 35Определение доходности (YTM)
Вы хотите определить доходность(YTM) по выпуску облигаций фирмой
(BW). BW выпустило облигации с 10% годовым купоном на срок
15 лет. Облигации имеют текущую рыночную стоимость $1,250.Какова доходность к погашению (YTM)?
Слайд 36Решение (пробуем 9%)
$1,250 = $100(PVIFA9%,15) +
$1,000(PVIF9%, 15)
$1,250 = $100(8.061) +
$1,000(.275)$1,250 = $806.10 + $275.00
= $1,081.10 [Ставка слишком высока!]
Слайд 37Решение (пробуем 7%)
$1,250 = $100(PVIFA7%,15) +
$1,000(PVIF7%, 15)
$1,250 = $100(9.108) +
$1,000(.362)$1,250 = $910.80 + $362.00
= $1,272.80 [Ставка слишком низкая!]
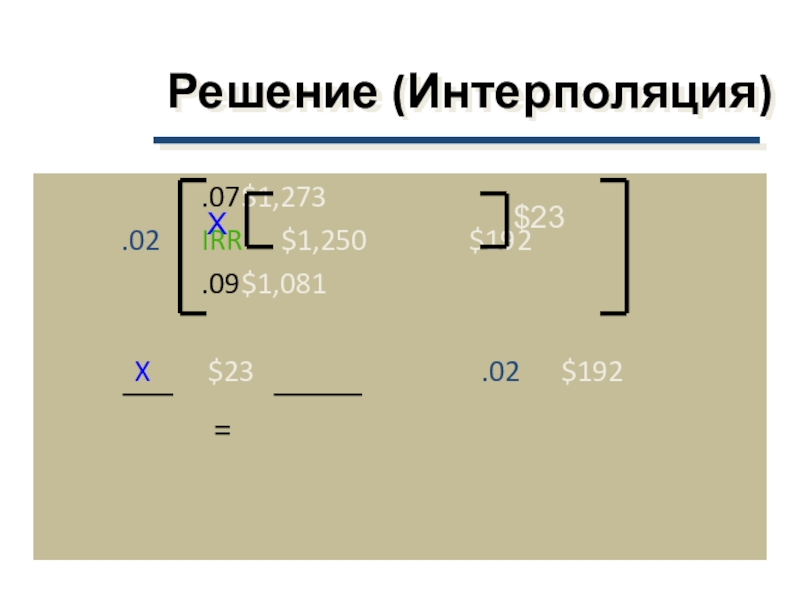
Слайд 40 .07 $1273
.02 YTM $1250 $192
.09 $1081
($23)(0.02) $192
Решение (интерполяция)
$23
X
X =
X = .0024
YTM
= .07 + .0024 = .0724 или 7.24%
Слайд 41Определение доходности облигации с полугодовым купоном
P0 =
S
2n
t=1
(1 + kd
/2 )t
I / 2
= (I/2)(PVIFAkd /2, 2n) + MV(PVIFkd /2
, 2n) +
MV
[ 1 + (kd / 2)2 ] -1 = YTM
Определите доходность к погашению (YTM) облигации с полугодовым купоном и определенным сроком.
(1 + kd /2 )2n
Слайд 42Определение YTM по облигации с полугодовым купоном
Вы хотите определить доходность
к погашению (YTM) для выпуска облигаций с 8% полугодовым купоном
со сроком погашения 20 лет. Текущая рыночная стоимость облигаций $950.Определите YTM?
Слайд 43Определение YTM по облигации с полугодовым купоном
[ 1 + (kd
/ 2)2 ] -1 = YTM
Определение доходности к погашению (
Yield-to-Maturity (YTM) для облигации с полугодовым купоном с ограниченным сроком.[ 1 + (.042626)2 ] -1 = .0871
или 8.71%
.
![Определение YTM по облигации с полугодовым купоном[ 1 + (kd / 2)2 ] -1 = YTMОпределение доходности](/img/tmb/7/644411/9fc72ceb8b17a90288354d3a47732a4c-800x.jpg "Лекция 4 Определение YTM по облигации с полугодовым купоном[ 1 + (kd /")
Слайд 44Соотношение стоимости и доходности облигации
Дисконт по облигации -- Величина, на
которую номинальная стоимость облигации превышает ее текущую, рыночную, цену, (Номинал
> P0 ), a YTM > купонной ставки облигации.Премия по облигации -- Величина, на которую текущая, рыночная, цена облигации превышает ее номинальную стоимость. (P0 > Номинала), a YTM < купонной ставки облигации.
По номиналу – Купонная ставка равна рыночной ставке доходности (P0 = номиналу), а YTM = купонной ставке облигации
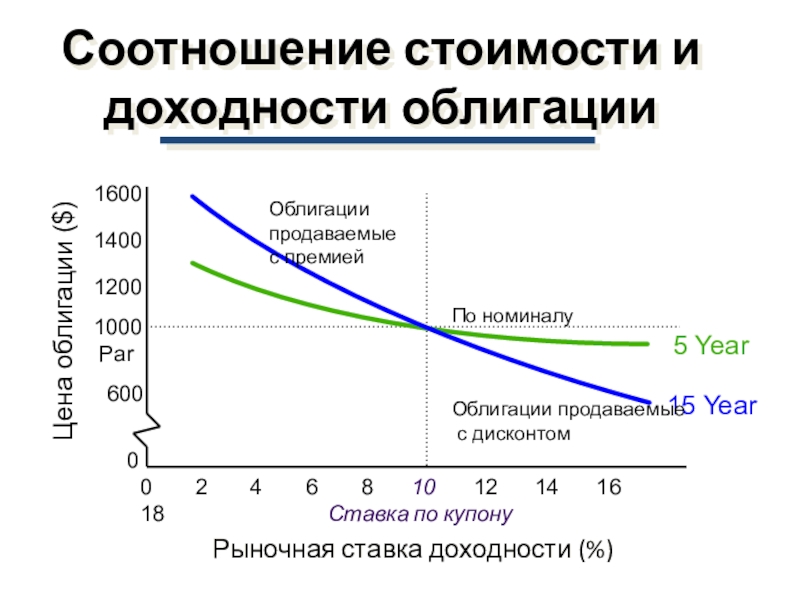
Слайд 45Соотношение стоимости и доходности облигации
Ставка по купону
Рыночная ставка
доходности (%)
Цена облигации ($)
1000
Par
1600
1400
1200
600
0
0 2
4 6 8 10 12 14 16 185 Year
15 Year
Облигации
продаваемые
с премией
По номиналу
Облигации продаваемые
с дисконтом
Слайд 46Соотношение стоимости и доходности облигаций
Допустим, что требуемая ставка доходности по
15-летним облигациям, с 10% годовым купоном выросла с 10% до
12%. Что произойдет с ценой облигации?Когда процентные ставки растут и происходит увеличение рыночной ставки доходности , тогда стоимость облигаций падает.
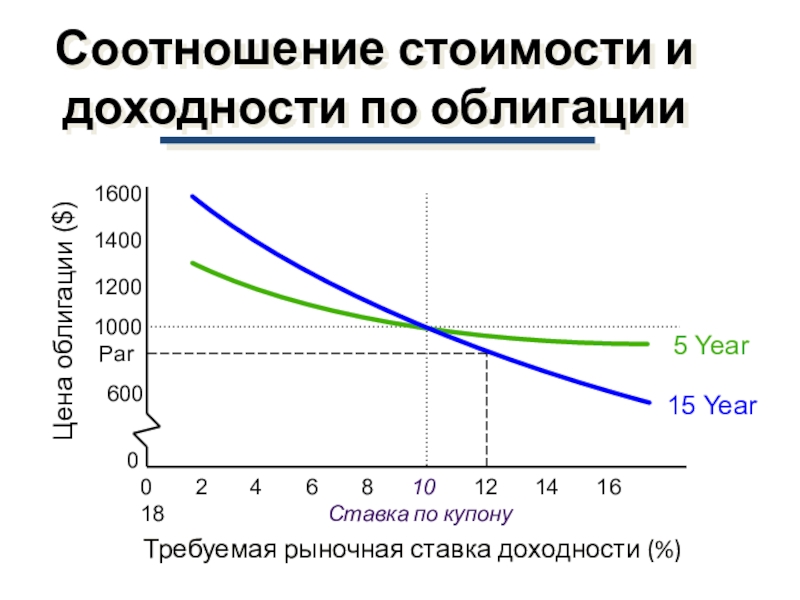
Слайд 47Соотношение стоимости и доходности по облигации
Ставка по купону
Требуемая
рыночная ставка доходности (%)
Цена облигации ($)
1000
Par
1600
1400
1200
600
0
0
2 4 6 8 10 12 14 16 1815 Year
5 Year
Слайд 48Соотношение цены и доходности при растущих ставках
Таким образом, цена облигации
упала с $1,000 до $864.
($863.78 на калькуляторе)
Требуемая ставка доходности по
15-летним облигациям с 10% годовым купоном поднялась с 10% до 12%.
Слайд 49Соотношение цены и доходности
Допустим, что требуемая ставка доходности по 15-летним
облигациям с 10% годовым купоном упала с 10% до 8%.
Что произойдет с ценой облигации?Когда процентные ставки падают, требуемая рыночная ставка доходности падает и цена облигации растет.
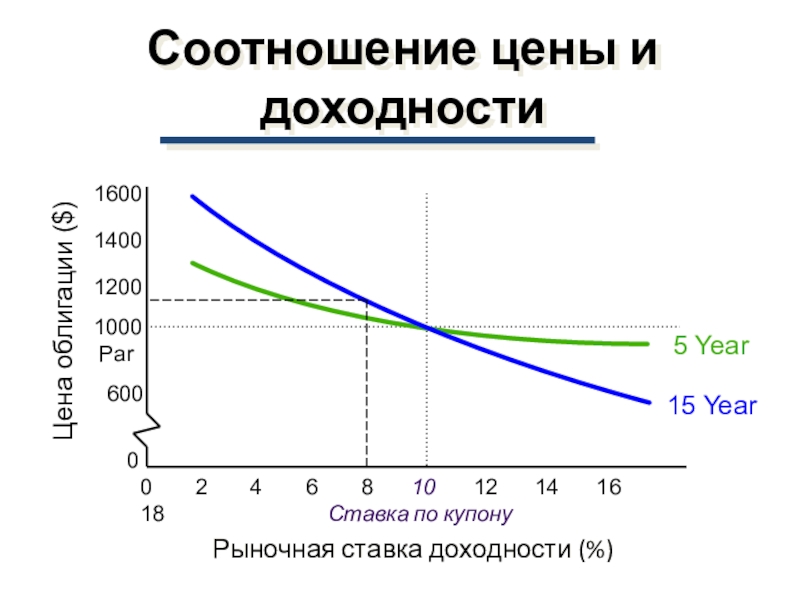
Слайд 50Соотношение цены и доходности
Ставка по купону
Рыночная ставка доходности
(%)
Цена облигации ($)
1000
Par
1600
1400
1200
600
0
0 2
4 6 8 10 12 14 16 1815 Year
5 Year
Слайд 51Соотношение цены и доходности при снижении ставок
Таким образом, цена
облигации выросла с $1000 до $1171.
($1,171.19 на калькуляторе)
Требуемая ставка доходности
по 15-летним облигациям с 10% купоном s упала с 10% до 8%.
Слайд 52Роль срока до погашения
Допустим, что требуемая ставка доходности по обеим
5 и 15-летним облигациям с 10% годовым купоном снизилась с
10% до 8%. Что произойдет с изменениями в цене облигаций?Чем длиннее срок облигации, тем больше изменение в цене при изменении рыночной ставки доходности.
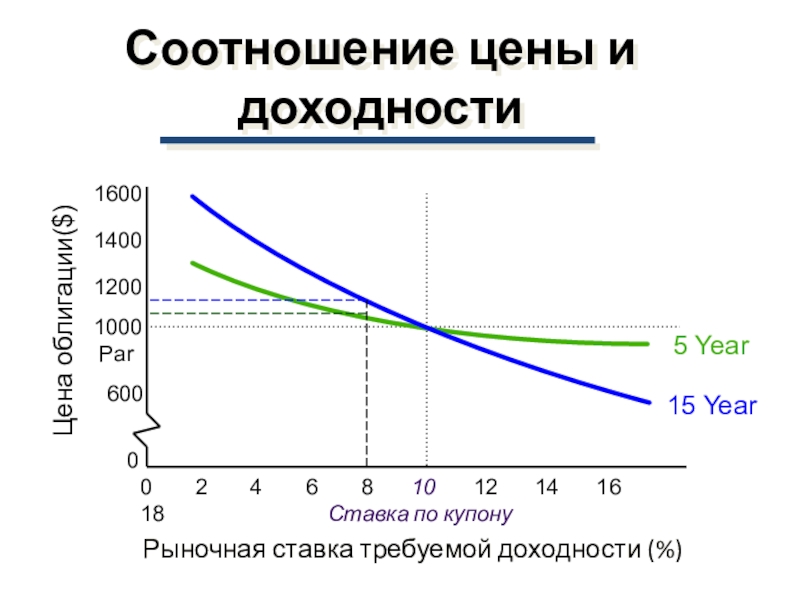
Слайд 53Соотношение цены и доходности
Ставка по купону
Рыночная ставка требуемой
доходности (%)
Цена облигации($)
1000
Par
1600
1400
1200
600
0
0 2
4 6 8 10 12 14 16 1815 Year
5 Year
Слайд 54Роль срока облигации
5 –летний бонд вырос в цене с $1,000
до $1,080, что составляет (+8.0%).
15-летний бонд вырос в цене с
$1,000 до $1,171 (+17.1%). В два раза быстрее!Требуемая ставка доходности по 5 и 15-летним облигациям с 10% годовым купоном упала с 10% до 8%.
Слайд 55Определение доходности по привилегированным акциям
Определение доходности по привилегированной акции с
неограниченным сроком действия.
P0 = DivP / kP
Из формулы находим
kP kP = DivP / P0
Слайд 56Пример определения доходности по привилегированной акции
kP = $10 / $100.
kP
= 10%.
Допустим, что годовой дивиденд по каждой привилегированной акции $10.
Каждая акция торгуется по $100. Определите доходность?
Слайд 57Определение доходности по обыкновенной акции
Применима модель постоянного роста дивидендов. Определим
доходность обыкновенной акции.
P0 = D1 / ( ke - g
)Из формулы находим ke
ke = ( D1 / P0 ) + g
Слайд 58Пример доходности обыкновенной акции
ke = ( $3 / $30 )
+ 5%
ke = 10% + 5% = 15%
Допустим, что ожидаемый
дивиденд (D1) по каждой акции равен $3. Каждая акция торгуется по $30 и имеет ожидаемый рост в 5%. Какова доходность акции?
Слайд 59источники
Основы финансового менеджмента
12-е издание
Джеймс К. Ван Хорн
Станфордский университет
Джон М. Вахович,
мл.
Университет штата Теннеси
© Pearson Education Limited 2004
Fundamentals of Financial Management,
12/eCreated by: Gregory A. Kuhlemeyer, Ph.D.
Carroll College, Waukesha, WI
