Слайд 1Лекция 5
1.Применение ЯМР-спектроскопии.
2.Импульсная спектроскопия.
3.Времена релаксации
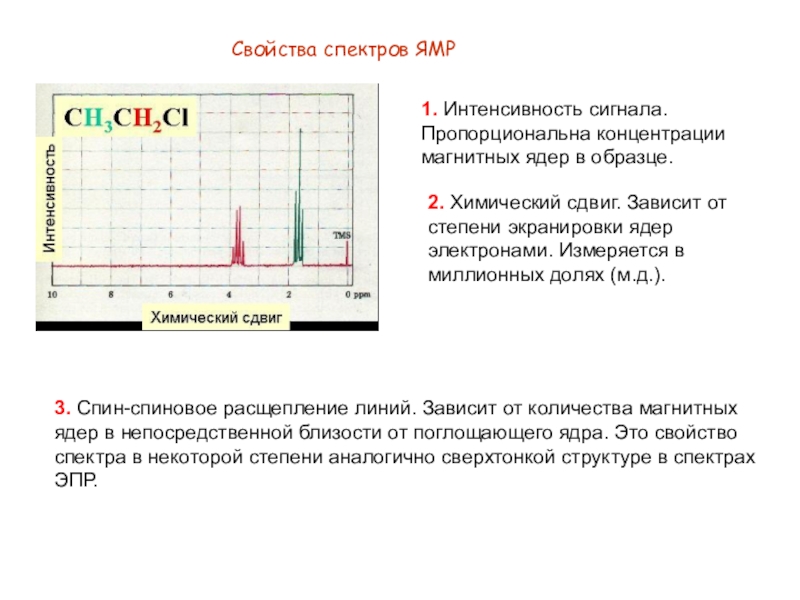
Слайд 3Свойства спектров ЯМР
1. Интенсивность сигнала. Пропорциональна концентрации магнитных ядер в
образце.
2. Химический сдвиг. Зависит от степени экранировки ядер электронами.
Измеряется в миллионных долях (м.д.).
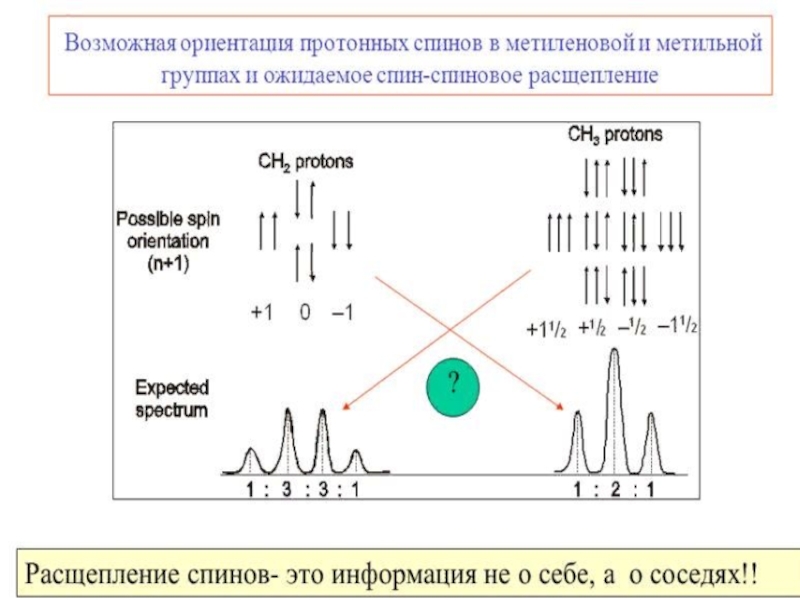
3. Спин-спиновое расщепление линий. Зависит от количества магнитных ядер в непосредственной близости от поглощающего ядра. Это свойство спектра в некоторой степени аналогично сверхтонкой структуре в спектрах ЭПР.
Слайд 7Применение в медико-биологических исследованиях
Исследование структуры белков с помощью 1Н-ЯМР высокого
разрешения и Фурье-преобразований.
Изучение свойств свободной и связанной воды помощью импульсного
1Н-ЯМР.
13С-ЯМР спектроскопия применяется для изучения белков, нуклеиновых кислот и других биологически важных соединений. Обладает большей чувствительностью, чем 1Н-ЯМР.
31Р-ЯМР спектроскопия часто применяется для исследования структуры и функций фосфолипидов.
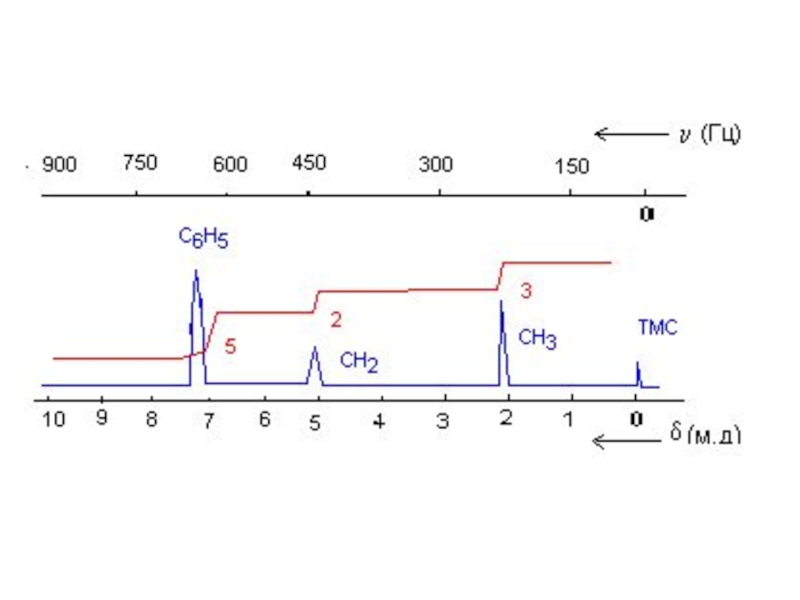
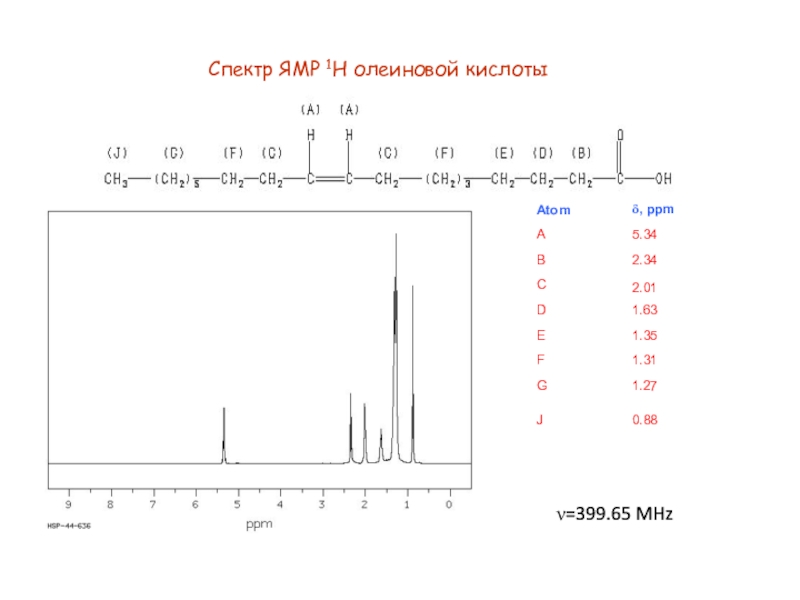
Слайд 8Спектр ЯМР 1H олеиновой кислоты
n=399.65 MHz
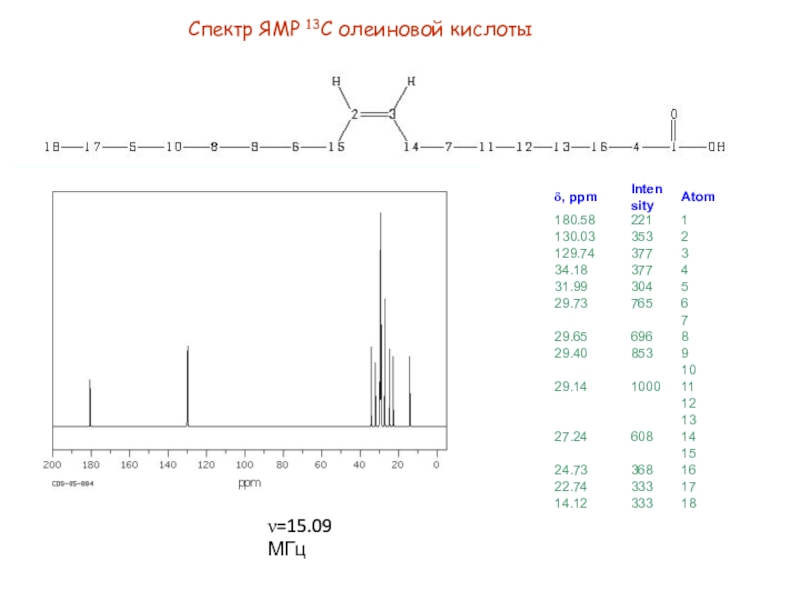
Слайд 9Спектр ЯМР 13С олеиновой кислоты
=15.09 МГц
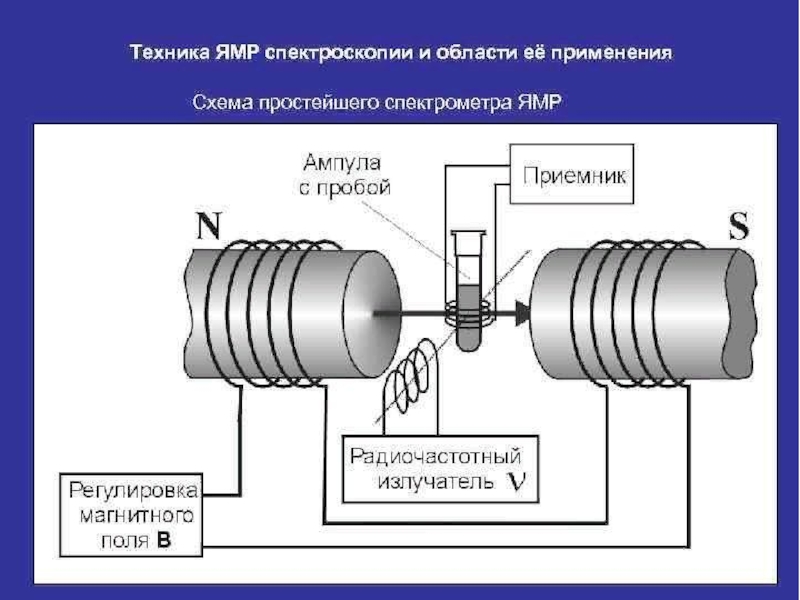
Слайд 14В импульсном варианте эксперимента ЯМР, в отличие от CW-метода, возбуждение
ядер осуществляют не "постоянной волной", а с помощью короткого импульса
продолжительностью (обычно несколько микросекунд). Радиочастотный генератор включают в момент t0 и выключают в момент t1. Продолжительность импульса зависит от ширины спектра. Например, если =10-5 сек, то частотная полоса будет шириной Гц. Выбор частоты генератора определяется величиной В0 и исследуемым изотопом.
Слайд 15
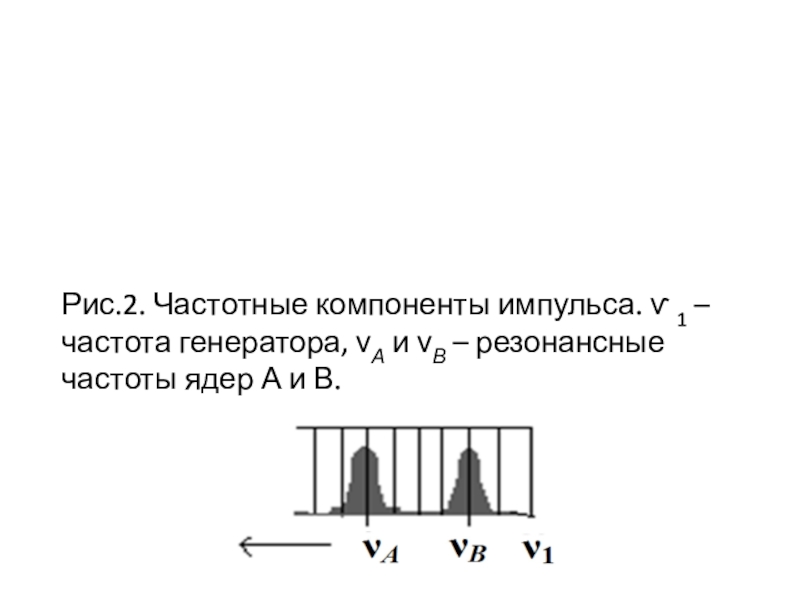
Рис.2. Частотные компоненты импульса. ѵ 1 – частота генератора, νА
и νВ – резонансные частоты ядер А и В.
Слайд 16Если среднее значение выбрано правильно, то все частоты в регистрируемом
спектре будут находиться в этой полосе (рис. 2). Амплитуды частотных
компонент импульса уменьшаются с увеличением расстояния от ѵ1. Так как желательно, чтобы все ядра облучались одинаково, необходимо использовать "жесткие импульсы", т.е. короткие импульсы большой мощности. Продолжительность импульса выбирают так, чтобы ширина частотной полосы была больше ширины спектра на один-два порядка. Мощность – несколько Ватт.
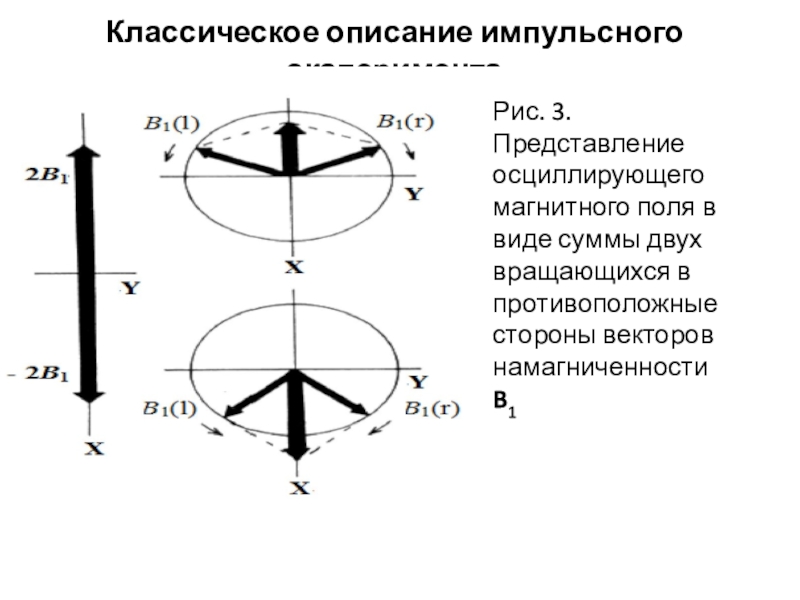
Слайд 17Классическое описание импульсного эксперимента
Рис. 3. Представление осциллирующего магнитного поля в
виде суммы двух вращающихся в противоположные стороны векторов намагниченности B1
Слайд 18Взаимодействующее с ядерными диполями радиочастотное поле B1 можно представить в
виде двух векторов одинаковой длины, вращающихся в плоскости X-Y в
противоположном направлении с частотой νL (сумма этих векторов = 2B1) (рис. 3). Это поможет понять, каким образом поле B1 взаимодействует с намагниченностью образца.
Дело в том, что радиочастотное поле не постоянно, и даже постоянная намагниченность образца, будучи отклоненной от оси Z, начнет совершать прецессирующее движение вокруг оси постоянного поля.
Слайд 19Чтобы исключить все вращения, достаточно вместо стационарной системы координат X,
Y, Z ввести новую (вращающуюся) систему координат X’, Y’, Z,
связанную с прецессией ядра. Если наша система координат будет вращаться с той же скоростью и в том же направлении, что и прецессия ядра, то магнитный момент каждого индивидуального ядра будет в ней постоянным. Вместе с исчезновением прецессии должна исчезнуть и ее причина – внешнее поле B0, которого в новой системе координат уже нет. Однако объемная намагниченность образца М0 остается по- прежнему направленной вдоль оси Z.
Слайд 20Поскольку частота поля B1 выбиралась равной ларморовской частоте, одна из
двух компонент, на которые его можно разложить, становится постоянной в
плоскости X’– Y’. Вторая, вращающаяся с той же частотой в противоположном направлении, в новой системе координат вращается вдвое быстрей и не оказывает существенного влияния. С ядерными диполями взаимодействует только та компонента, которая имеет одинаковое с ними направление вращения, т.е. первая. Под влиянием этой компоненты намагниченность M0 отклоняется от оси Z, причем отклонение происходит в плоскости, перпендикулярной B1.
Слайд 21Во вращающейся системе координат X', Y', Z ориентация и величина
B1 будут фиксированы. Угол поворота вектора намагниченности или угол импульса
будет равен:
Теоретически, включая поле на различные промежутки времени, можно повернуть вектор намагниченности на любой угол , где каждые 360° будут возвращать намагниченность в начальное положение.
Слайд 22Если напряженность поля В1 велика, а продолжительность импульса
настолько мала, что в течение импульса релаксационными процессами
можно пренебречь, то действие поля В1 сведется к повороту вектора намагниченности М на угол .Если величины В1 и выбраны
таким образом, что ,
то вектор М после поворота окажется в плоскости X’ – Y’. Такие импульсы называют импульсами поворота на угол 90°.
Слайд 23Те импульсы, для которых
, называют
импульсами поворота
на 180° . Действие последних на вектор намагниченности М приводит к изменению его первоначального направления на противоположное. В большинстве импульсных методик используются
= 90° и
=180° (рис. 4).
Слайд 24Рис. 4. Ориентация вектора макроскопической ядерной намагниченности М0 во вращающейся
системе координат: после произвольного -градусного импульса
(а); после π/2-импульса (б); после π-импульса (в). Волнистая линия вдоль оси Х показывает ориентацию эффективного поля B1.
Слайд 25Все импульсы с продолжительностью
, отличной от π/2, оставляют некоторую часть Z-намагниченности, не создающей
сигнала ССИ (здесь и далее ССИ означает спад свободной индукции, иногда это явление называют ССН - свободный спад намагниченности). Только ее компонента в плоскости X’–Y’ (поперечная намагниченность My') способна создавать напряжение в катушке приемника. Таким образом, импульс π/2, (или теоретически 3 π/2, 5 π/2, и т.д.) создает максимальный сигнал.
Слайд 26И, напротив, импульс 180° x' (или 2π, 3π, …) вообще
не вызывает появления сигнала, поскольку он помещает намагниченность на ось
Z (здесь и далее – будет соответствовать радиочастотному импульсу, поворачивающему равновесную намагниченность M0 на угол вокруг обозначенной оси (индекс внизу) во вращающейся системе координат) (рис. 4). Таким образом, максимальные сигналы наблюдаются при = 90° , т.к. важнейшей является поперечная намагниченность My', ибо катушка приемника ориентирована вдоль оси Y’. Для = 180° -ного импульса сигналы не наблюдаются.
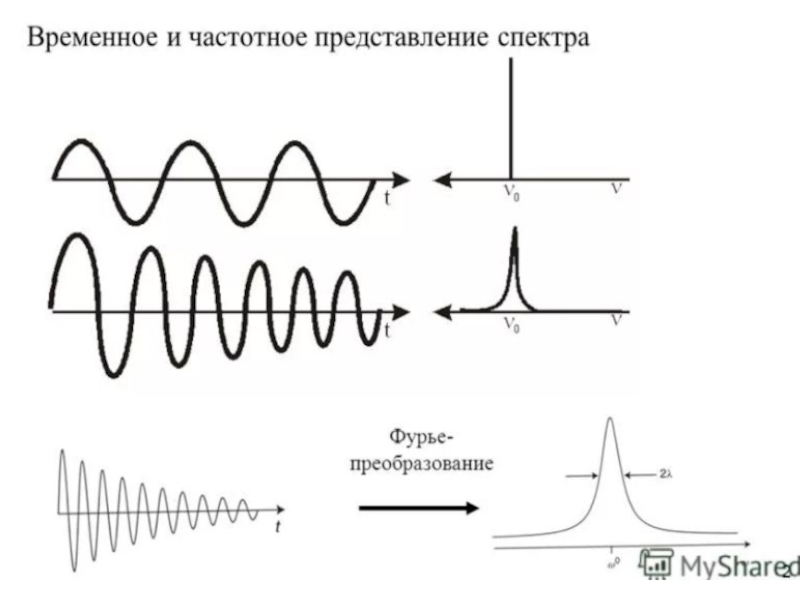
Слайд 27Фурье-преобразование
Какая разница между сигналами, которые наблюдаются в экспериментах с
непрерывной разверткой (стационарный ЯМР) и в импульсном эксперименте?
В методе
непрерывной развертки, меняя частоту радиочастотного поля В1, измеряют зависимость амплитуды от частоты (измерение в частотном представлении). При регистрации данных после импульса измеряют то, как амплитуда развивается во времени (временное представление).
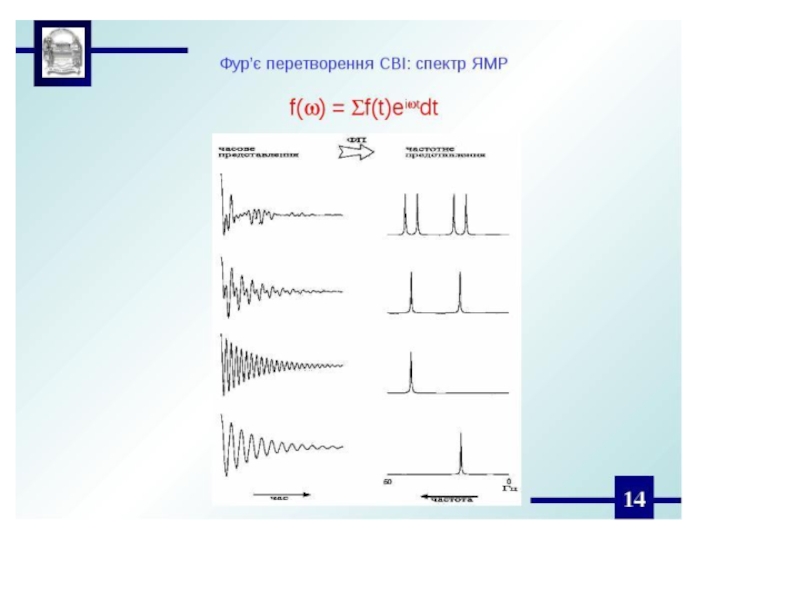
Слайд 28Преобразование Фурье (1) - это математическая операция, которая преобразует функцию
от времени в частотные компоненты и позволяет переходить от одного
представления к другому и является обычным методом анализа результатов импульсных экспериментов :
где i мнимая единица (комплексная величина, равная
f (t) соответствует спектру "временного представления", а f (w) - спектру "частотного представления".
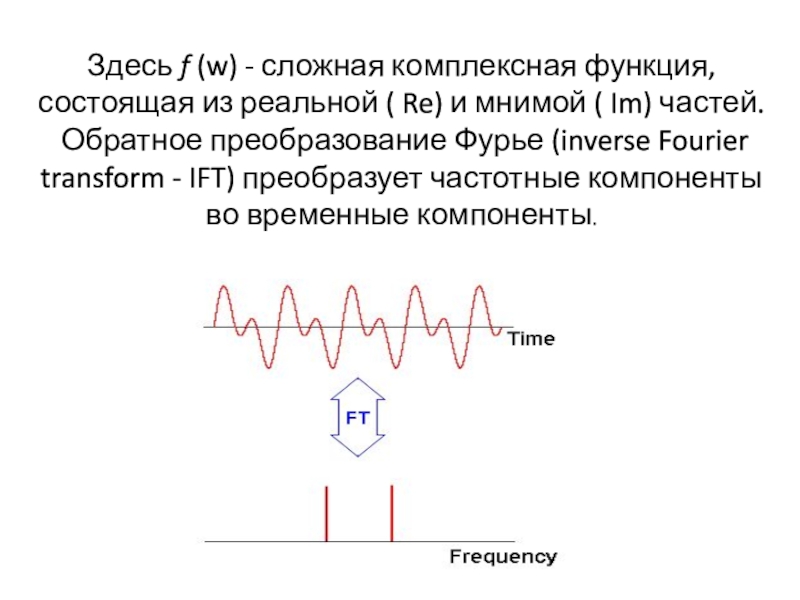
Слайд 29Здесь f (w) - сложная комплексная функция, состоящая из реальной
( Re) и мнимой ( Im) частей.
Обратное преобразование Фурье
(inverse Fourier transform - IFT) преобразует частотные компоненты во временные компоненты.
Слайд 30Если в образце содержатся ядра с различными резонансными частотами или
спектр образца представляет собой мультиплет вследствие спин-спинового взаимодействия, то кривые
спада различных компонент поперечной намагниченности накладываются друг на друга и имеет место интерференция между несколькими ССИ.
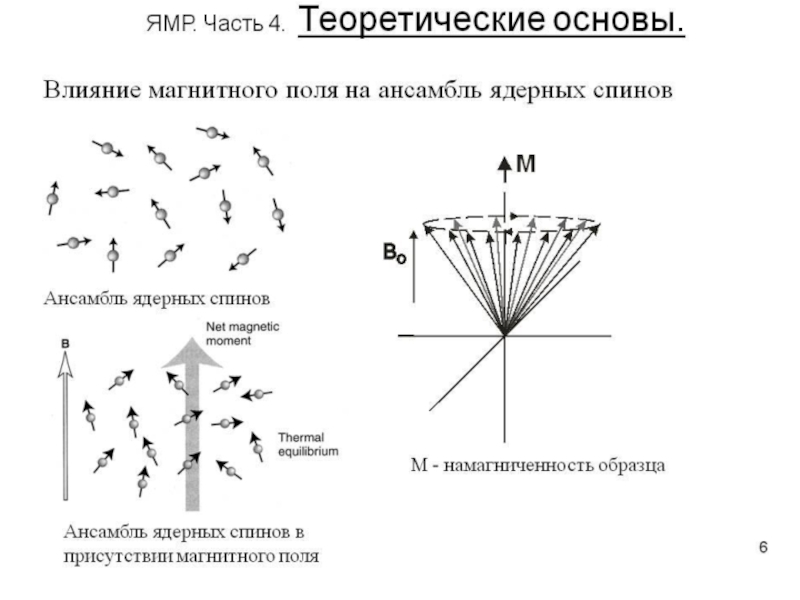
Слайд 34При включении радиочастотного поля вектор M0 отклоняется от равновесного положения
на угол . Если постоянное магнитное поле В0
совершенно однородно, то поведение вектора намагниченности М0 после окончания действия импульса определяется процессами релаксации, т.е. спиновая система возвращается к равновесному состоянию посредством релаксации (Mz → M0, а Mx и My → 0).
Слайд 35Блох предположил, что релаксационные процессы имеют первый порядок и могут
быть описаны двумя различными временами релаксации Т1 и T2, определяемыми
уравнениями
для вращающейся системы координат (X',Y', Z): где T1 - время спин-решеточной или продольной релаксации, а T2 - время спин-спиновой или поперечной релаксации.
Слайд 36Обратные значения величин
и соответствуют константам скоростей релаксации. Движение вектора М при наличии
процессов релаксации представляет собой прецессию с одновременным уменьшением угла между М и направлением поля В0. Чтобы представить себе это
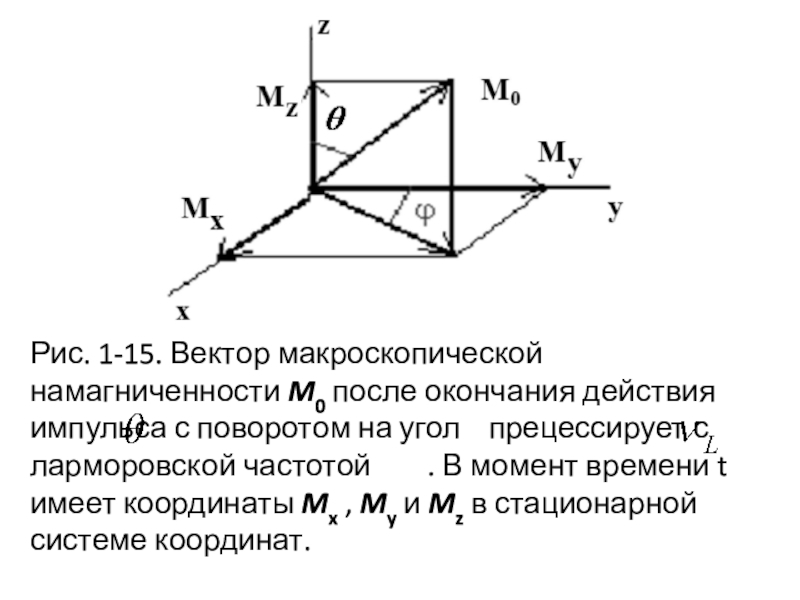
движение, разложим вектор М на компоненты и рассмотрим их как функции времени (рис. 1-15).
Слайд 37Рис. 1-15. Вектор макроскопической намагниченности M0 после окончания действия импульса
с поворотом на угол прецессирует с ларморовской частотой
. В момент времени t имеет координаты Mx , My и Mz в стационарной системе координат.
Слайд 38Компонента, расположенная в плоскости X–Y, будет вращаться вокруг направления поля
В0 (ось Z), в то время как ее амплитуда будет
стремиться к нулю по экспоненциальному закону exp (-t/T2). В то же время амплитуда компоненты Мz будет, уменьшаясь, стремиться к своему равновесному значению (Mz → M0) за промежуток времени Т1. Нет причин предполагать, что все линии сложного спектра будут релаксировать с одной и той же скоростью, поэтому следует ожидать существование набора различных констант Т1 для разных ядер молекулы.
Слайд 39Из конечного времени жизни возбужденного состояния вытекает конечная ширина линии
в частотном спектре. Ширина линии измеряется на полувысоте сигнала ЯМР
(рис. 1-16). Поскольку время ЯМР-релаксации в растворах в большинстве случаев довольно велико (несколько минут), резонансные линии в спектре ЯМР оказываются довольно узкими в сравнении, например, с УФ-спектрами поглощения.
Слайд 40Почему время релаксации Т1 обычно велико?
Для ответа на этот
сложный вопрос понадобилось бы несколько книг, поэтому обсудим его здесь
на качественном уровне. Прежде всего, необходимо отметить, что небольшие энергии ЯМР-переходов настолько малы в сравнении с их общей тепловой энергией, что с их рассеянием не возникает никаких проблем. Следовательно, релаксация замедляется не по причине невозможности рассеяния энергии, а из-за недостатка путей ее вывода из спиновой системы.
Слайд 41Их добавляют в образец, если нужно сократить время релаксации для
ускорения эксперимента или для повышения точности количественных измерений. Для этой
цели обычно используется ацетилацетонат хрома (III).
Экспериментально время спин-решеточной или продольной релаксации T1 измеряется с использованием последовательности импульсов
с различными значениями времени . Анализ зависимости изменения интенсивности сигнала от угла поворота равновесной намагниченности M0 позволяет достаточно просто определить искомое время T1.
Слайд 42Время T2 - время спин-спиновой или поперечной релаксации определяется по
аналогичному алгоритму, но с использованием иной последовательности импульсов, а именно:
Теперь выясним, что происходит с поперечной намагниченностью после окончания действия импульса в во вращающейся системе координат.
Слайд 43Если выбрать оси X ’ и Y ' так, что
высокочастотное
поле В1 будет направлено по оси X ’, то вектор
макроскопической намагниченности M0 в момент t = 0 будет расположен вдоль оси Y '. Т.к. эта ось вращается с частотой ларморовской прецессии ядер , то компонента My' остается постоянной или, более точно, ее величина уменьшается во времени со скоростью, определяемой потерями через релаксацию. В соответствии с выражением (1-16), это уменьшение экспоненциально, и его скорость обусловлена временем поперечной релаксации T2 (рис. 1-17).
Слайд 44Рис. 1-17. Спад поперечной намагниченности
Слайд 45«Cпадающие» кривые, подобные представленной на рис. 1-17 (вверху), в реальных
экспериментах не наблюдаются, так как используемые методы детектирования предполагают получение
их только в тех случаях, когда частота генератора и резонансная частота наблюдаемых ядер случайно совпадают.
Все процессы, сопровождающиеся потерей поперечной намагниченности, включая возвращение ее на ось Z, дают вклад в величину Т2.
Слайд 46Таким образом, при отсутствии всех механизмов поперечной релаксации время Т2
должно равняться времени Т1, поскольку переход намагниченности на ось Z
будет, очевидно, сопровождаться уходом ее из плоскости X –Y. При нормально настроенной однородности поля В0 такая ситуация довольно часто встречается в жидкостях.
Слайд 47Фазовая когерентность
Проиллюстрируем экспериментально, не вдаваясь в детали, уравнение (1-15).
Из этого уравнения следует, что угол поворота вектора намагниченности можно
увеличить, либо увеличив амплитуду компоненты Bi либо увеличив продолжительность импульса . В экспериментах Фриболина с образцом H2O увеличивали с интервалом в 1 мкс, а Bi выдерживали постоянной.
Слайд 48Из полученных результатов следует, что максимум амплитуды соответствует
, а
там, где сигнал проходит через нуль , (рис. 1-18). Очевидно также, что большие значения дают отрицательную амплитуду сигнала, что объясняется появлением поперечной намагниченности - My' при .
Слайд 49Рис. 1-18. Зависимость амплитуды сигнала ЯМР воды от угла поворота
импульса
Слайд 50Что касается населенностей энергетических уровней, то при
ситуация обращается и ядер на верхнем энергетическом уровне окажется больше, чем на нижнем уровне. При имеем
более сложную ситуацию, т.к. Mz = 0 и оба зеемановских уровня заселены равным образом. Этот случай отличается от насыщения, т.к.
в данной ситуации у нас имеется My', а при насыщении - нет.
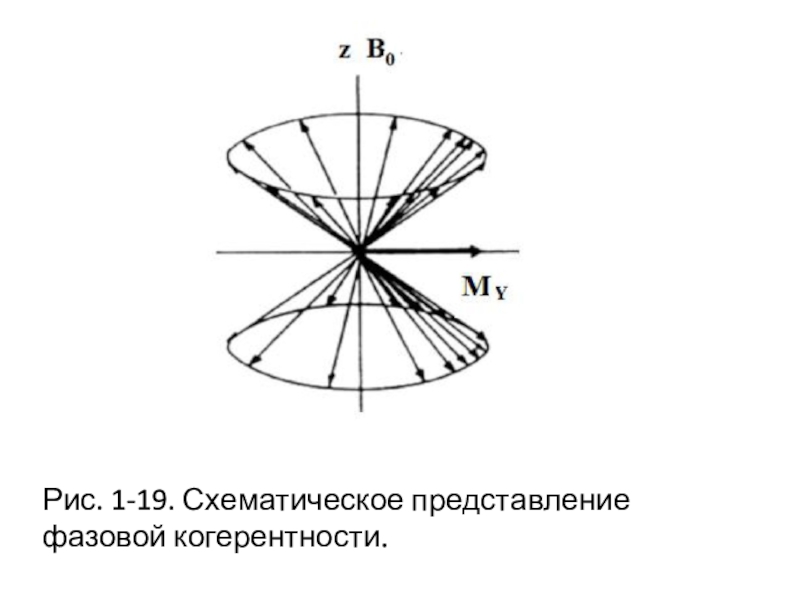
Слайд 51Появление поперечной намагниченности в данном случае объясняется тем, что под
влиянием B1 ядерные диполи прецессируют вокруг двойного конуса не равномерно,
а образуя "редкие" и "плотные" фракции, прецессирующие "по фазе". Это явление - "фазовая когерентность" (рис. 1-19).
Слайд 52Рис. 1-19. Схематическое представление фазовой когерентности.