Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛЕКЦИЯ 5 ЗАКОНЫ И СРЕДСТВА ЛАНДШАФТНОЙ КОМПОЗИЦИИ (ПРОДОЛЖЕНИЕ) План Основные
Содержание
- 1. ЛЕКЦИЯ 5 ЗАКОНЫ И СРЕДСТВА ЛАНДШАФТНОЙ КОМПОЗИЦИИ (ПРОДОЛЖЕНИЕ) План Основные
- 2. метр и ритм, симметрия и асимметрия,
- 3. АНА – («вновь, снова, повторно») ЛОГОС –
- 4. Суть всех концепций пропорций – установление закономерной упорядоченности, которая способна привести композицию к гармонии и единству.
- 5. Организующим началом в архитектуре и дизайне часто служит простейшее повторение тождественных элементов
- 6. Процесс решения композиционных задач с помощью пропорций
- 7. В архитектуре гармоническое соотношение пространственных величин можно
- 8. АРИФМЕТИЧЕСКИЕ ПРОПОРЦИИ – такие отношения, в которых
- 9. Наиболее простая соизмеримость выражается в отношении 1:1 (квадрат).
- 10. Садовый павильон
- 11. Слайд 11
- 12. По мере увеличения чисел отношение усложняетсяЕгипетский треугольник,
- 13. ГЕОМЕТРИЧЕСКИЕ (ИРРАЦИОНАЛЬНЫЕ) ПРОПОРЦИИ – такие соотношения, которые
- 14. Повторение форм крупных частей в более мелких
- 15. Спасо-Преображенская церковь.18 в. с. Нижняя Синячиха
- 16. а) отношение диагонали квадрата к его сторонеб) отношение высоты равностороннего треугольника к половине его основания
- 17. Построение динамических прямоугольниковК геометрическим отношениям относятся и динамические прямоугольники
- 18. Динамические прямоугольники
- 19. Иоганн Кеплер говорил, что геометрия владеет двумя
- 20. Слайд 20
- 21. История золотого сеченияПринято считать, что понятие о
- 22. В дошедшей до нас античной литературе золотое
- 23. Леонардо ФибоначчиРяд Фибоначчи 1, 1, 2,
- 24. Так, 21 : 34 = 0,617, а
- 25. В 1509 г. в Венеции была издана книга
- 26. «Бог всегда действует геометрически» (Платон), т.е. божественной
- 27. астроном XVI в. Иоганн Кеплерзолотая пропорция продолжает
- 28. немецкий живописец и график Альбрехт Дюрер (1471...1528).Альбрехт
- 29. Золотые пропорции в фигуре человека (По
- 30. Золотые пропорции в частях тела человека
- 31. Яйцо птицы ЯщерицаВетка цикорияЯрким
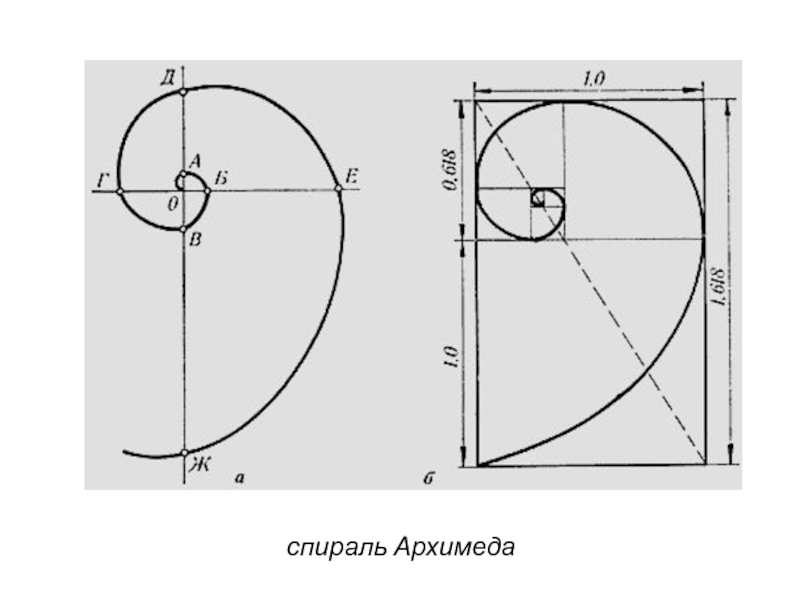
- 32. спираль Архимеда
- 33. Дорифор,Ск. ПоликтетВенера МилосскаяЭталоном красоты человеческого тела считаются творения греческих скульпторов
- 34. Пропорции Давида ( Микеланджело) основаны на Золотом сечении
- 35. Русский кристаллограф Г.В. Вульф (1863...1925) считал золотое сечение
- 36. a : b = b : (a + b) b — ab — a = 0 b = a · 1,618
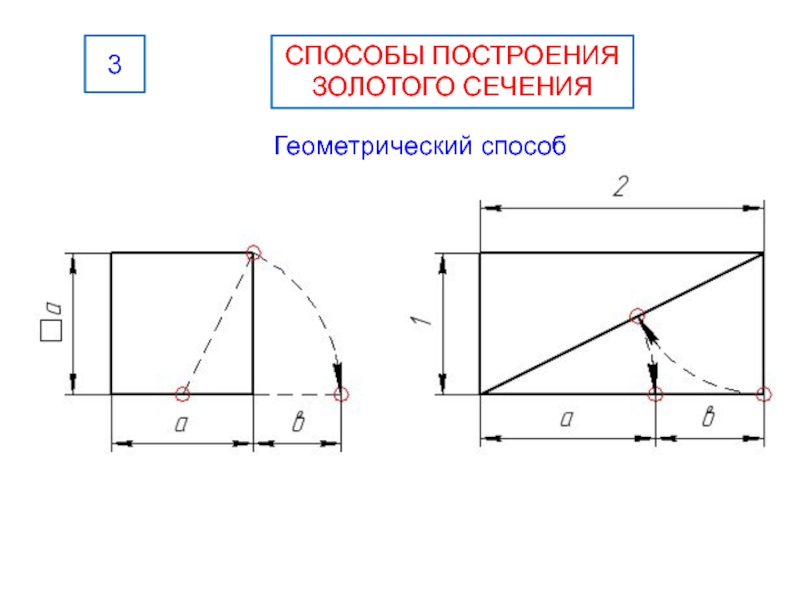
- 37. Геометрический способ 3СПОСОБЫ ПОСТРОЕНИЯ ЗОЛОТОГО СЕЧЕНИЯ
- 38. Если необходимо вычислить меньшую сторону исходя из большей,
- 39. Если целый отрезок принять за 100 частей, то большая часть отрезка равна 62,а меньшая — 38 частям
- 40. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью
- 41. «Золотым» называется прямоугольник, стороны которого находятся в отношении 1.618 :1
- 42. Строим квадрат ABEF Сторону AF делим пополам
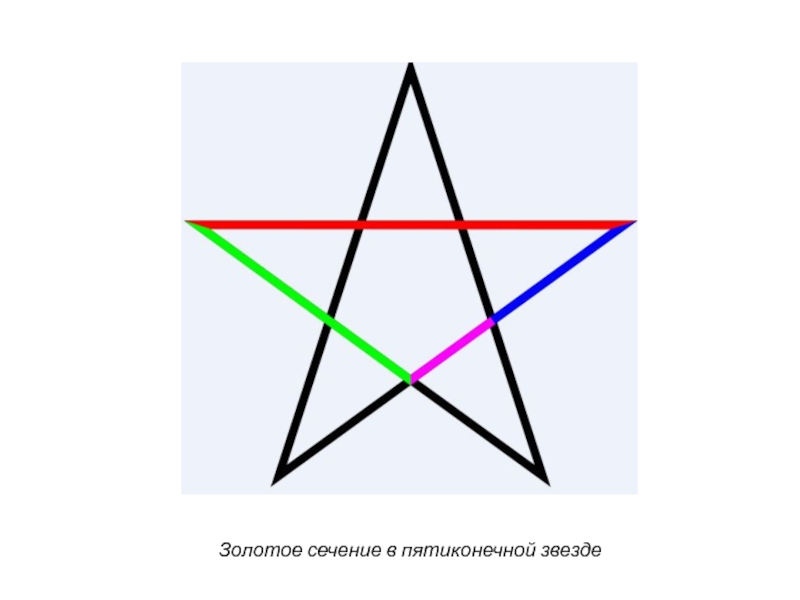
- 43. Золотое сечение в пятиконечной звезде
- 44. Построения пентаграммы. Способ его построения разработал Альбрехт Дюрер
- 45. Прямоугольник приблизительно золотого сечения, построенный на основании пятиугольника
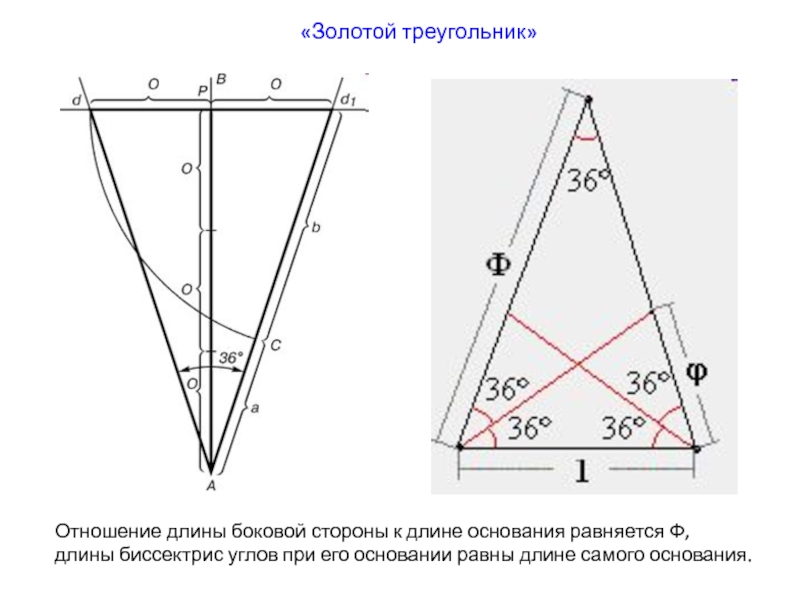
- 46. «Золотой треугольник»Отношение длины боковой стороны к длине
- 47. Композиционное построение картины «Джоконда» основано на двух
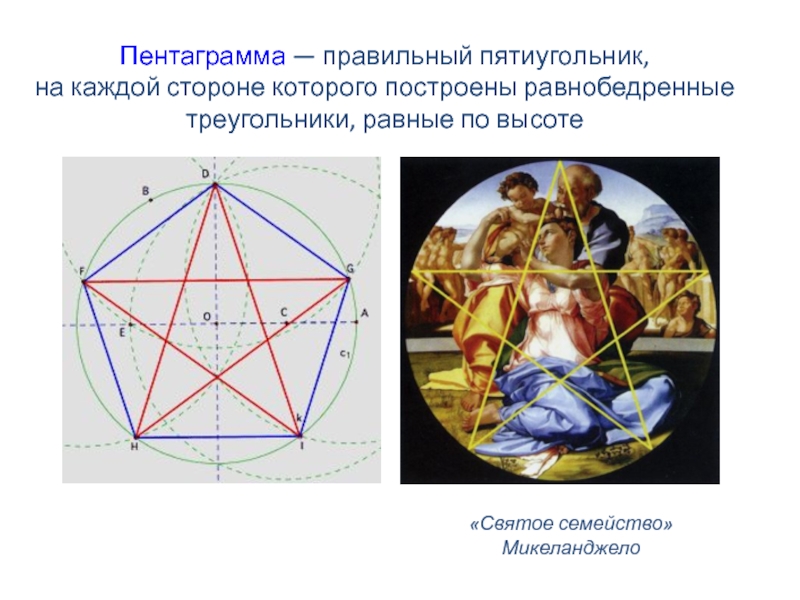
- 48. Пентаграмма — правильный пятиугольник, на каждой стороне
- 49. Есть и золотой кубоид – это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
- 50. В ландшафтном искусстве золотое сечение используется при
- 51. На практике часто используется совмещение двух видов
- 52. В модульной системе пропорций за основу берется
- 53. Марк Дорф
- 54. Слайд 54
- 55. Так, кратные соотношения 1:2; 1:3; 1:4 дают
- 56. Универсальным модулем парковых пространств является человек. Французский
- 57. Исходными единицами измерения в этой системе служат
- 58. Слайд 58
- 59. Скачать презентанцию
метр и ритм, симметрия и асимметрия, контраст и нюанс, масштабность, статика и динамика, цвет, свет, пропорцииОсобое средство гармонизации композиции – тектоникаК художественным средствам создания единства композиции относятся:
Слайды и текст этой презентации
Слайд 1
ЛЕКЦИЯ 5
ЗАКОНЫ И СРЕДСТВА ЛАНДШАФТНОЙ КОМПОЗИЦИИ (ПРОДОЛЖЕНИЕ)
План
Основные приемы построения пропорций
Золотое
сечение
Слайд 2 метр и ритм,
симметрия и асимметрия,
контраст
и нюанс,
масштабность,
статика и динамика,
цвет,
свет,
пропорцииОсобое средство гармонизации композиции – тектоника
К художественным средствам создания единства
композиции относятся:
Слайд 3
АНА – («вновь, снова, повторно»)
ЛОГОС – во времена Платона
«отношения»
ПРОПОРЦИИ – «вновь-отношения» –
повторяющиеся отношения
1
ОСНОВНЫЕ ПРИЕМЫ ПОСТРОЕНИЯ
ПРОПОРЦИЙ
Латинским словом
ПРОПОРЦИИ древний римский оратор Цицерон перевел греческое слово АНАЛОГИЯПРОПОРЦИЯ
ЧТО ЭТО ТАКОЕ?
Слайд 4Суть всех концепций пропорций – установление закономерной упорядоченности, которая способна
привести композицию к гармонии и единству.
Слайд 5Организующим началом в архитектуре и дизайне часто
служит простейшее повторение
тождественных элементов
Слайд 6Процесс решения композиционных задач с помощью пропорций называется пропорционированием. В
теорию ландшафтного искусства пропорции, так же как и остальные средства
композиции, пришли из архитектуры.Луксор
Др. Египет
Слайд 7В архитектуре гармоническое соотношение пространственных величин можно разделить на 2
группы:
– простые (арифметические), строящиеся на отношениях простых чисел,
–
иррациональные(геометрические), получаемые при помощи геометрического построения.
Слайд 8АРИФМЕТИЧЕСКИЕ ПРОПОРЦИИ – такие отношения, в которых
числовая зависимость двух
величин выражается дробным числом,
где числитель и знаменатель – целые
числа в пределах от 1 до 6В простых отношениях мы имеем
простую числовую и ясно читаемую
соизмеримость пространственных
величин, что и является одним из
условий их гармонической связи.
Слайд 12
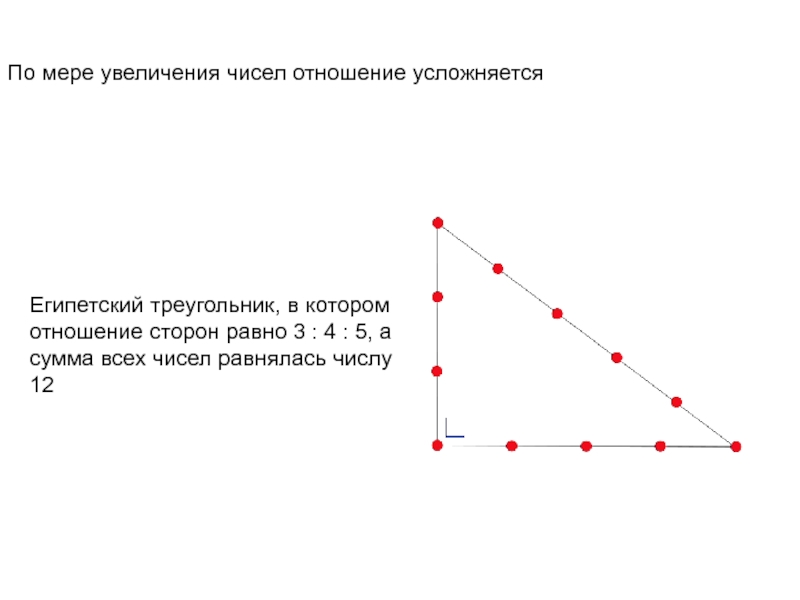
По мере увеличения чисел отношение усложняется
Египетский треугольник, в котором отношение
сторон равно 3 : 4 : 5, а сумма всех
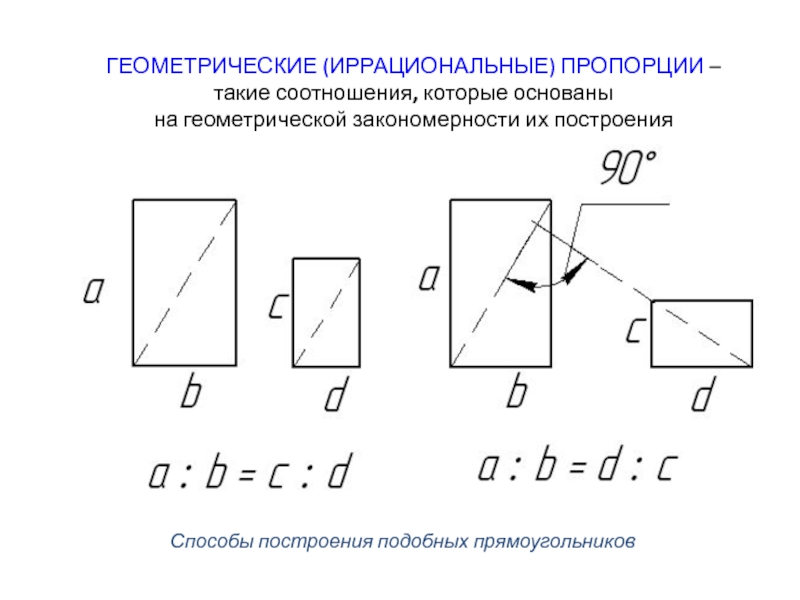
чисел равнялась числу 12
Слайд 13ГЕОМЕТРИЧЕСКИЕ (ИРРАЦИОНАЛЬНЫЕ) ПРОПОРЦИИ –
такие соотношения, которые основаны
на геометрической
закономерности их построения
Способы построения подобных прямоугольников
Слайд 14Повторение форм крупных частей в более мелких деталях
Палаццо Ручеллаи.
Флоренция Луи-Батист Альберти
Схема по Тиршу
Слайд 16а) отношение диагонали квадрата к его стороне
б) отношение высоты равностороннего
треугольника к половине его основания
Слайд 17Построение динамических прямоугольников
К геометрическим отношениям
относятся и динамические прямоугольники
Слайд 19Иоганн Кеплер говорил,
что геометрия владеет
двумя сокровищами –
теоремой Пифагора
и золотым сечением.
И если первое из этих двух
сокровищ можно
сравнить с мерой золота, то второе
с драгоценным камнем. Теорему Пифагора знает
каждый школьник,
а что такое золотое
сечение – далеко не все.
2
ЗОЛОТОЕ СЕЧЕНИЕ
Слайд 20
Золотое сечение - это такое пропорциональное
деление отрезка
на неравные части, при котором весь отрезок так
относится к большей части, как сама большая часть относится к меньшей;
или другими словами, меньший отрезок так относится к большему,
как больший ко всему
АВ : АC = АC : ВC
или
ВС : АС = АВ:АС
Приближенно это отношение равно 5/3, точнее 8/5, 13/8 и т.д.
Слайд 21История золотого сечения
Принято считать, что понятие о золотом делении ввел
в научный обиход
Пифагор, древнегреческий философ и математик (VI в.
до н.э.) 
Слайд 22В дошедшей до нас античной литературе золотое деление впервые
упоминается в
"Началах" Евклида. Во 2-й книге "Начал" дается
геометрическое построение золотого
деления. Секреты золотого деления хранились в строгой тайне
Слайд 23Леонардо Фибоначчи
Ряд Фибоначчи
1, 1, 2, 3, 5, 8, 13,
21, 34, 55, 89, 144...
каждый член ряда, начиная с третьего,
равен сумме двух предыдущих
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13,
8 + 13 = 21;
13 + 21 = 34 и т.д.,
где n - натуральное число
и начальные члены равны 1 и 1.
Слайд 24Так, 21 : 34 = 0,617, а 34 : 55
= 0,618.
Это отношение обозначается символом Ф.
Отношение смежных чисел
ряда приближается к отношениюзолотого сечения.
Слайд 25В 1509 г. в Венеции была
издана книга Луки Пачоли
«Божественная
пропорция»
С иллюстрациями
Леонардо да Винчи.
«божественная суть»
золотой пропорции в
том, что малый отрезок
есть олицетворение
бога сына, больший отрезок –
бога отца, а весь отрезок –
бога духа святого.
Лука Пачоли
Леонардо да Винчи ввёл термин «ЗОЛОТОЕ СЕЧЕНИЕ»
Слайд 26«Бог всегда действует геометрически» (Платон), т.е. божественной пропорцией — «золотым
сечением» — делением целого так, чтобы отношение большей части к
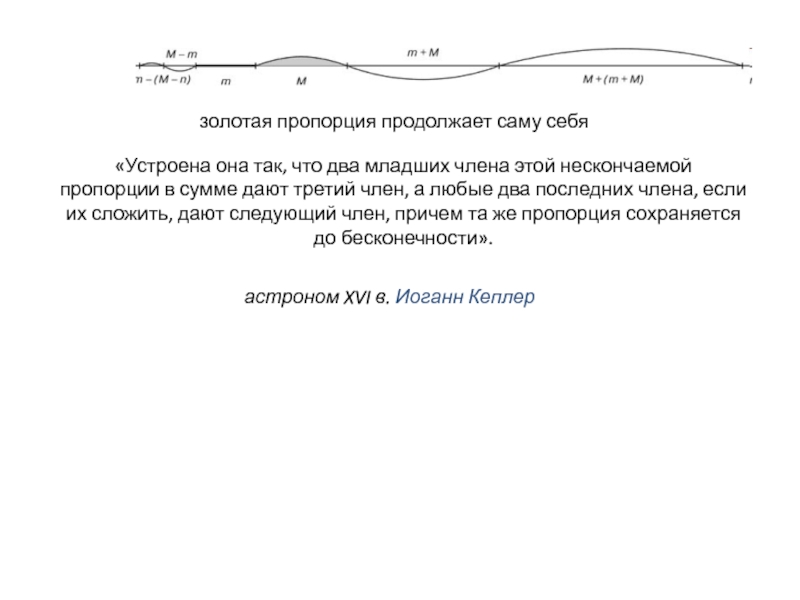
меньшей равнялось отношению всего целого к большей его части.
Слайд 27астроном XVI в. Иоганн Кеплер
золотая пропорция продолжает саму себя
«Устроена
она так, что два младших члена этой нескончаемой
пропорции в
сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется
до бесконечности».
Слайд 28немецкий живописец и график Альбрехт Дюрер (1471...1528).
Альбрехт Дюрер подробно
разрабатывает
теорию пропорций
человеческого тела.
Рост человека делится
в золотых пропорциях
линией пояса, а также линией,
проведенной через кончики
средних пальцев опущенных рук,
нижняя часть лица - ртом и т.д.
Известен пропорциональный
циркуль Дюрера.
Слайд 29Золотые пропорции в фигуре человека
(По теории Цейзинга )
Пропорции
женского тела
8 : 5 = 1,6
Пропорции
мужского тела
13 : 8 = 1,625
Пропорции
новорожденного
1:1
Слайд 30Золотые пропорции в частях тела человека
(По теории Цейзинга )
Цейзинг
рассматривал золотое сечение как основной
морфологический закон в природе и
искусстве. Он показал, что этот закон проявляется в пропорциях
тела человека
Слайд 31
Яйцо птицы
Ящерица
Ветка цикория
Ярким примером проявления чисел Фибоначчи в
живой природе
является филлотаксис
Слайд 33
Дорифор,
Ск. Поликтет
Венера Милосская
Эталоном красоты человеческого тела считаются
творения греческих скульпторов
Слайд 35Русский кристаллограф Г.В. Вульф (1863...1925)
считал золотое сечение одним из проявлений
симметрии.
Статическая симметрия характеризует покой, равновесие,
а динамическая – движение,
рост. Существует
статическая и динамическая симметрия
Слайд 36a : b = b : (a + b) b — ab — a = 0 b = a · 1,618 Или b = 1,618 · a, и a = 0,618 · b (обратное число числа a,
т. е. 1 : а = 1 : 1,618 = 0,618)
2
2
Слайд 38Если необходимо вычислить меньшую сторону исходя
из большей, то необходимо умножить длину
большей
на 0,618. Если нужна большая сторона - умножить длину
меньшей на 1,618
Определение золотого сечения с помощью
«золотого» числа
Слайд 39Если целый отрезок принять за 100 частей,
то большая часть отрезка равна
62,
а меньшая — 38 частям
Слайд 40Отрезки золотой пропорции выражаются бесконечной
иррациональной дробью 0,618...,
если c
принять за единицу, a = 0,382.
Числа 0.618 и 0.382
являются коэффициентами последовательности Фибоначчи.
На этой пропорции базируются основные геометрические фигуры
Слайд 42
Строим квадрат ABEF
Сторону AF делим пополам точкой D.
Строим
окружность с центром в точке D и радиусом DB.
Нас
интересует точка пересечения окружности с продолжением стороны AFВосстанавливаем перпендикуляр в точке M к прямой AF.
Продлеваем BE до пересечения с перпендикуляром.
Слайд 46«Золотой треугольник»
Отношение длины боковой стороны к длине основания равняется Ф,
длины биссектрис углов при его основании равны длине самого основания.
Слайд 47Композиционное построение картины «Джоконда» основано на двух золотых треугольниках, повернутых
друг к другу своими основаниями
Леонардо Да Винчи использовал пропорции Золотого
сечения во многих своих самых знаменитых произведениях
Слайд 48Пентаграмма — правильный пятиугольник,
на каждой стороне которого построены равнобедренные
треугольники, равные
по высоте
«Святое семейство»
Микеланджело
Слайд 49Есть и золотой кубоид – это прямоугольный
параллелепипед с ребрами,
имеющими длины 1.618, 1 и 0.618.
Слайд 50В ландшафтном искусстве золотое сечение используется при создании цветников и
партеров, в соотношениях размеров планировочных элементов и при построении композиций
пейзажных картин, хотя его применение затруднено из-за возрастной динамики насаждений.
Слайд 51На практике часто используется совмещение двух видов пропорциональных отношений (арифметических
и геометрических), чаще всего используются 2 вида пропорционирования: модульная система
пропорций и золотое сечение.
Слайд 52В модульной системе пропорций за основу берется некая единая исходная
величина, которая служит мерой пространственного построения (или единицей измерения) композиции,
она называется модулем (от лат. — мера).МОДУЛЬНЫЕ ОТНОШЕНИЯ – 2 : 3, 3 : 4, 2 : 5, 3 : 5, 4 : 5, 5 : 6 –
содержат в себе модуль, укладывающийся целое и небольшое
число раз в каждой величине
Простые (модульные) отношения
Слайд 55Так, кратные соотношения 1:2; 1:3; 1:4 дают в прямоугольной форме
повторение квадрата целое число раз, меньшая величина служит модулем большей.
Например, ширина парковой дорожки определяется удобством прохода и количеством бетонных плит, укладываемых на нее. В качестве модуля используется отрезок в 75 см. Ширина дорожки соответственно будет 1,5, 2,25, 3 м и т. д. Расстояние между древесными группами при их размещении в пространстве измеряется диаметром проекции их крон; ширина поляны —высотой ее опушки; расстояние от точки наблюдения до воспринимаемого объекта — его высотой (известно, что минимальные размеры этого расстояния должны быть равны двойной, лучше тройной высоте объекта).
Слайд 56Универсальным модулем парковых пространств является человек. Французский арх. Ле Корбюзье
предложил систему пропорций «модулор», основанную на математически определенных соотношениях человеческого
роста и его частей.
Слайд 57Исходными единицами измерения в этой системе служат величины членений человеческого
тела. В ландшафтном искусстве, ориентированном на создание комфортной среды для
человека, такой подход представляется очень важным. Интересно, что «в модулоре» Ле Корбюзье каждое последующее членение связано с предыдущим.
