Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 7 1.Понятие корреляционной зависимости Коэффициент
Содержание
- 1. Лекция 7 1.Понятие корреляционной зависимости Коэффициент
- 2. 1.Понятие корреляционной зависимости Коэффициент корреляцииОпределение. Зависимость между
- 3. В корреляционном и регрессионном анализе изучается взаимосвязь
- 4. 2. Справедливо неравенствоД.3. Если, то между У и Х существует линейная функциональная связь.(7.3)Д.
- 5. 2.Корреляционное поле. Выборочный коэффициент корреляции.Х и У – случайные величиныНет связиСлабая связьвыборкаКорреляционное поле- уравнение прямой
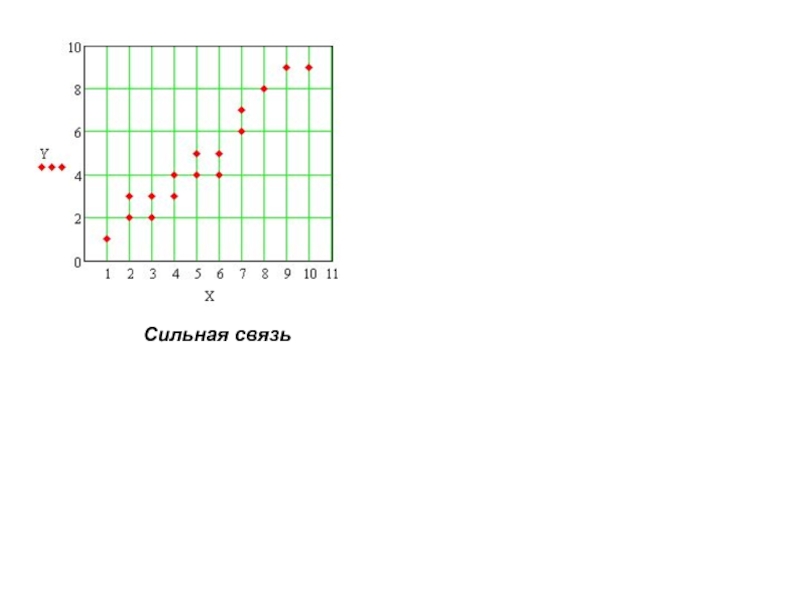
- 6. Сильная связь
- 7. Выборочный коэффициент корреляции определяется по формулеЗамечания.Выборочный коэффициент
- 8. 3.Регрессионная модельИсследуемый объектxYСостояние объекта характеризуется различными параметрами.
- 9. - уравнение регрессии у на хЛинейная регрессионная
- 10. Слайд 10
- 11. (7.8 ) - выборочный
- 12. Пример. При исследовании эффективности агротехнических мероприятий получены
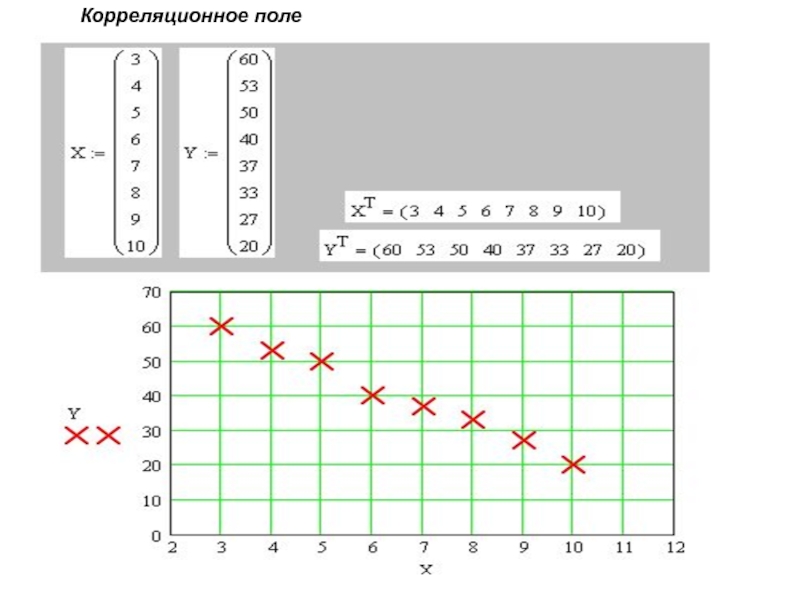
- 13. Корреляционное поле
- 14. Расчетная таблица
- 15. Выборочный коэффициент корреляцииУравнение регрессии у на хВыборочный коэффициент регрессии
- 16. xy6,544053,77
- 17. Значимость коэффициента корреляцииH0: =0H1: 2.
- 18. Слайд 18
- 19. Скачать презентанцию
1.Понятие корреляционной зависимости Коэффициент корреляцииОпределение. Зависимость между случайными величинами Х и У , при которой каждому значению Х соответствует некоторое распределение У называется статистической (стохастической). Если каждому значению Х соответствует некоторая
Слайды и текст этой презентации
Слайд 1Лекция 7
1.Понятие корреляционной зависимости Коэффициент корреляции.
2.Корреляционное поле. Выборочный коэффициент корреляции.
3.Регрессионная
модель.
квадратов.
Слайд 21.Понятие корреляционной зависимости Коэффициент корреляции
Определение.
Зависимость между случайными величинами Х
и У , при которой каждому значению Х соответствует некоторое
распределение У называется статистической (стохастической).Если каждому значению Х соответствует некоторая числовая характеристика У, то такая зависимость называется статистической корреляцией.
2. Х- количество внесенных удобрений; У- урожайность
Если значению одной величины ставится в соответствие единственное значение другой, то такая зависимость называется функциональной.
Пример. Х - число бракованных деталей в партии, У - стоимость бракованных деталей.
k – стоимость одной детали
Примеры.
1. Х – рост студента первого курса; У- вес студента первого курса
Слайд 3В корреляционном и регрессионном анализе изучается взаимосвязь случайных величин.
Две основные
задачи:
Определение силы (или тесноты связи)
Определение формы связи ( в виде
формулы) между двумя или несколькими случайными величинами.Коэффициент корреляции определяется по формуле
Основные свойства коэффициента корреляции
(7.1)
1. Если Х и У независимы, то коэффициент корреляции равен нулю:
(7.2)
Слайд 42. Справедливо неравенство
Д.
3. Если
, то между У и Х существует
линейная функциональная связь.
(7.3)
Д.
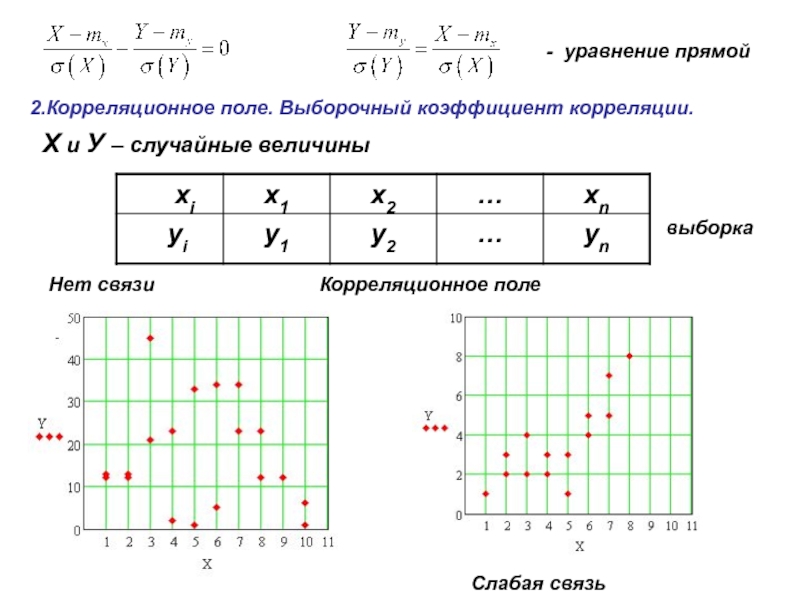
Слайд 52.Корреляционное поле. Выборочный коэффициент корреляции.
Х и У – случайные величины
Нет
связи
Слабая связь
выборка
Корреляционное поле
- уравнение прямой
Слайд 7Выборочный коэффициент корреляции определяется по формуле
Замечания.
Выборочный коэффициент корреляции – статистическая
оценка коэффициента корреляции
1.
2.
(7.4)
(7.5)
В выборке функциональная связь
3.
В выборке связи
нет
Слайд 83.Регрессионная модель
Исследуемый объект
x
Y
Состояние объекта характеризуется различными параметрами.
Предполагается, что У
зависит от х
У – результат (отклик)
Те переменные, которые по
мнению исследователя оказывают влияние на величину результата У, называют факторами.Фактор х влияет существенно;
Факторы
оказывают несущественное влияние
отклик
закономерная составляющая
случайная величина, независимая от х
(7.6)
Слайд 9- уравнение регрессии у на х
Линейная регрессионная модель:
4.Линейная регрессия. Оценка
параметров и методом наименьших квадратов
- выборочное
уравнение регрессииНормальная система метода наименьших квадратов имеет вид
(7.7)
Слайд 12Пример. При исследовании эффективности агротехнических мероприятий получены данные об объеме
(%) задерживаемых осадков микрорельефом на склонах различной крутизны (град)
Х –
крутизна склона (град)У – объем задерживаемых осадков (%)
Требуется:
1.Вычислить выборочный коэффициент корреляции
2.Найти выборочное уравнение регрессии у на х и построить прямую регрессии
3.Проверить гипотезу о значимости коэффициента корреляции
Слайд 17Значимость коэффициента корреляции
H0: =0
H1:
2. =0,05
3, Статистический критерий
Имеет
распределение Стьюдента с параметром
4. Находим критическую область
5. Наблюдаемое значение
критерияH0 отвергается
