Слайд 1Лекция 8
Принцип резолюции для ИВ и ИП 1 порядка
Слайд 2Определения
Определение 1 Литерой назовём атом A или его отрицание (A).
Назовём
А положительной литерой, A - отрицательной литерой.
Определение 2 Формулу вида
L1L2 …Ln назовём дизъюнктом. Здесь Li – литеры.
Определение 3 Дизъюнкты, соединённые знаками &, образуют КНФ.
Определение 4 Контрарной парой называется пара литер L, L, одна из которых является отрицанием другой.
Простое преобразование, позволяющее представить произвольную формулу (без кванторов) в КНФ, основано на тождестве:
X Y&Z = (X Y)&(X Z)
Пример. Привести к КНФ формулу A B (C D&E).
A B (C D&E) = A B (C D)& (C E) =
= (A B C D)& (A B C E)
Слайд 3Получение множества дизъюнктов
В предыдущей лекции было показано,
что последовательным применением алгоритма приведения к ПНФ, алгоритма Сколема и
алгоритма приведения к КНФ с сохранением свойства невыполнимости любая формула F может быть представлена набором дизъюнктов, объединенных кванторами общности. Такую формулу будем называть формулой, представленной в Сколемовской стандартной форме (ССФ).
В дальнейшем формулы вида x1 x2 … xr [D1 & D2 & … & Dk],
где D1, D2, …, Dk –дизъюнкты, а x1, x2, …, xr – различные переменные, входящие в эти дизъюнкты, будет удобно представлять как множество дизъюнктов S = {D1, D2, …, Dk}.
Например, множеству дизъюнктов
S = {P(x, f(x)), P(x, y) R(x, g(y)), Q(x) P(x, a)}
соответствует следующая формула, представленная в ССФ:
x y (P(x, f(x)) & (P(x, y) R(x, g(y))) & (Q(x) P(x, a))).
И, наконец, когда говорят, что множество дизъюнктов S = {D1, D2, …, Dk} невыполнимо (противоречиво), то всегда подразумевают невыполнимость формулы x1 x2 … xr [D1 & D2 & … & Dk], где x1, x2, …, xr – различные переменные, входящие в дизъюнкты.

Слайд 4Резольвента
Основная идея принципа резолюции заключается в проверке, содержит ли множество
дизъюнктов S пустой (ложный) дизъюнкт . Если это так, то
S невыполнимо. Если S не содержит , то следующие шаги заключаются в выводе новых дизъюнктов до тех пор, пока не будет получен (что всегда будет иметь место для невыполнимого S). Таким образом, принцип резолюции рассматривается как правило вывода, с помощью которого порождаются новые дизъюнкты из S.
По существу принцип резолюции является расширением правила modus ponens на случай произвольных дизъюнктов с любым числом литер. Действительно, имея P и P Q, что равносильно P Q, можно вывести Q путем удаления контрарной пары P и P. Расширение состоит в том, что если любые два дизъюнкта С1 и С2, имеют контрарную пару литер (P и P), то, вычеркивая ее, мы формируем новый дизъюнкт из оставшихся частей двух дизъюнктов. Этот вновь сформированный дизъюнкт будем называть резольвентой дизъюнктов С1 и С2.
Слайд 5Получение резольвенты
Пример 1 Пусть даны два дизъюнкта
C1: P Q
R,
C2: P Q.
Тогда их резольвента С: Q R.
Обоснованность
получения таким образом резольвенты вытекает из следующей теоремы.
Теорема. Резольвента С, полученная из двух дизъюнктов С1 и С2, является логическим следствием этих дизъюнктов.
Если в процессе вывода новых дизъюнктов мы получим два однолитерных дизъюнкта, образующих контрарную пару, то резольвентой этих двух дизъюнктов будет пустой дизъюнкт .
Таким образом, выводом пустого дизъюнкта из невыполнимого множества дизъюнктов S называется конечная последовательность дизъюнктов С1, С2, …, Сk такая, что любой Ci (i =1, 2,…, k) является или дизъюнктом из S, или резольвентой, полученной принципом резолюции, и Сk = .
Слайд 6Пример 2
Вывод пустого дизъюнкта может быть наглядно представлен с помощью
дерева вывода, вершинами которого являются или исходные дизъюнкты, или резольвенты,
а корнем – пустой дизъюнкт.
Пример 2. Пусть S:
1. P Q,
2. P Q,
3. P Q,
4. P Q.
Тогда резольвентами будут:
5. Q (1, 2),
6. Q (3, 4),
7. (5, 6).
Далее на рисунке представлено дерево вывода
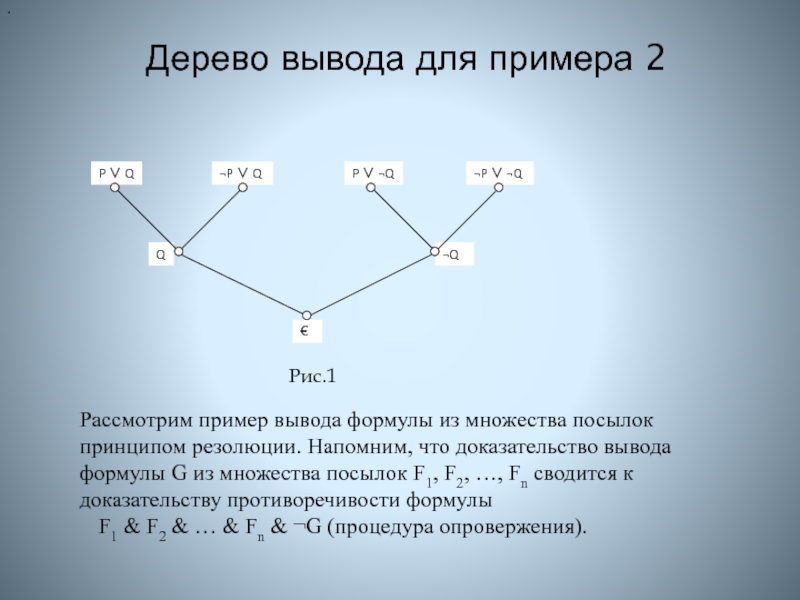
Слайд 7 Дерево вывода для примера 2
.
Рис.1
Рассмотрим пример вывода формулы из множества посылок принципом резолюции. Напомним, что доказательство вывода формулы G из множества посылок F1, F2, …, Fn сводится к доказательству противоречивости формулы
F1 & F2 & … & Fn & G (процедура опровержения).
Слайд 8Пример 3
Горничная сказала, что она видела дворецкого в гостиной.
Гостиная находится рядом с кухней. Выстрел раздался на кухне и
мог быть услышан во всех близлежащих комната. Дворецкий, обладающий хорошим слухом, сказал, что он не слышал выстрела. Детектив должен доказать, что если горничная сказала правду, то дворецкий солгал.
P Q: если горничная сказала правду, то дворецкий был в гостиной.
Q R: если дворецкий был в гостиной, то он находился рядом с кухней.
R L: если дворецкий был рядом с кухней, то он слышал выстрел.
M L: если дворецкий сказал правду, то он не слышал выстрела.
Требуется доказать, что если горничная сказала правду, то дворецкий солгал, т.е. P M.
Представим посылки в КНФ: (P Q) & (Q R) & (R L) & (M L).
Аналогично заключение: P M.
Доказательство «от противного» требует построить опровержение заключения: (P M ) = P&M .
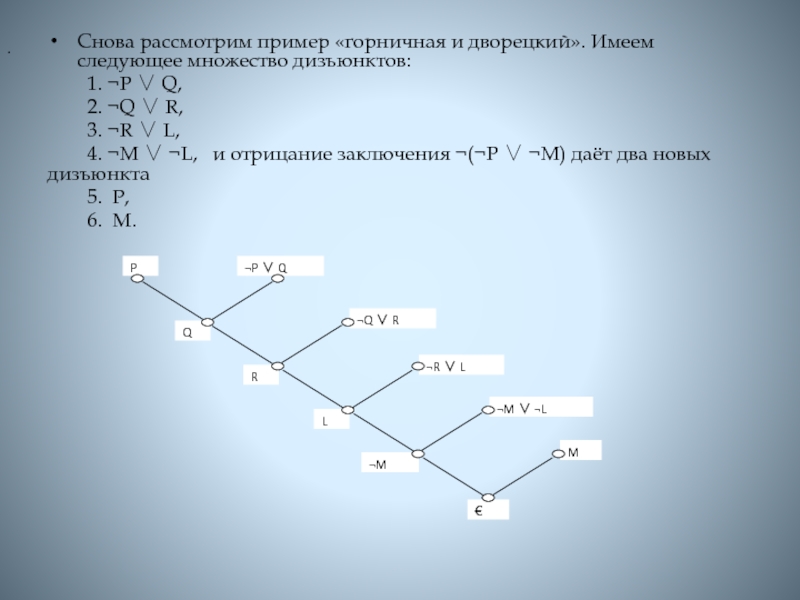
Слайд 9Снова рассмотрим пример «горничная и дворецкий». Имеем следующее множество дизъюнктов:
1.
P Q,
2. Q R,
3. R L,
4. M
L, и отрицание заключения (P M) даёт два новых дизъюнкта
5. P,
6. M.
.
Слайд 10Замечание
Если среди дизъюнктов S или полученных позже резольвент найдётся дизъюнкт
– тавтология (такой дизъюнкт включает литеры L и L), то
такой дизъюнкт можно вычеркнуть: если S невыполнимо, то оно останется невыполнимыми после вычёркивания тавтологии.
Рассмотрим дизъюнкты из примера 2:
1. P Q,
2. P Q,
3. P Q,
4. P Q.
Резольвента дизъюнктов 2 и 3 например, по паре контрарных литер Р и Р даст нам резольвенту Q Q (склеиваем остатки дизъюнктов после вычеркивания контрарной пары). Ясно, что такая резольвента является тавтологией и её следует исключить из множества дизъюнктов.
Слайд 11Рассмотрим задачу:
Если капиталовложения останутся постоянными (К), то возрастут
правительственные расходы (R) или возникнет безработица (В). Если правительственные расходы
не возрастут, то налоги будут снижены (N). Если налоги будут снижены и капиталовложения останутся постоянными, то безработица не возникнет. Капиталовложения останутся постоянными. Следовательно, правительственные расходы возрастут.
Перейдём от формального представления утверждений
F1: KRB
F2: R N
F3: N&K B
F4: K
--------------------------
R
к множеству дизъюнктов:
(1) K RB
(2) R N
(3) N K B
(4) К
(5) R (добавляем отрицание заключения)
и докажем противоречивость этого множества.
Слайд 12Пример (продолжение)
(1) K RB
(2) R N
(3) N K
B
(4) К
(5) R
------------------------
(6) K N R
(резольвента 1,3)
(7) KR (резольвента 2,6)
(8) R (резольвента 4,7)
(9) (резольвента 5,8)
K RB N K B
K N R R N
KR К
R R
Слайд 13Принцип резолюции для логики предикатов
Если в логике высказываний нахождение контрарных
пар не вызывает трудностей, то для логики предикатов это не
так. Для нахождения контрарной пары необходимо сделать две литеры идентичными, для этого будем использовать подстановки.
Действительно, если мы имеем дизъюнкты типа
C1: P(x) R(x),
C2: P(g(y)) Q(y),
то резольвента может быть получена только после применения к С1 подстановки g(y) вместо х.
Имеем C1: P(g(y)) R(g(y)), ( в С1 заменяем везде х на g(y) )
C2: P(g(y)) Q(y),
Резольвента C: R(g(y)) Q(y).
Однако для случая
C1: P(f(x)) R(x),
C2: P(g(y)) Q(y),
очевидно, никакая подстановка в контрарную пару неприменима и никакая резольвента не образуется.
Слайд 14Использование подстановок
Правило использования подстановок можно сформулировать так:
Заменять можно только переменную.
Переменную
можно заменять
на другую переменную;
на константу;
на терм.
Заменять константу на переменную, либо
сложное выражение на простое нельзя.
Пример. D = P(x, f(y)) Q(z) дизъюнкт, содержащий переменные x, y, z.
Используем подстановку ={a/x, g(b)/y, f(a)/z} Получим дизъюнкт D’
D’ =D= P(a, f(g(b)) Q(f(a)
Дадим определение подстановки.
Слайд 15Подстановка
Подстановкой будем называть конечное множество вида {t1/x1, t2/x2, …, tn/xn},
где любой ti – терм, а любая xi – переменная
(1 i n), отличная от ti.
Подстановка называется фундаментальной, если все ti (1 i n), являются фундаментальными термами. Подстановка, не имеющая элементов, называется пустой подстановкой и обозначается через .
Пусть = {t1/x1, t2/x2, …, tn/xn} – подстановка и W – выражение. Тогда W будем называть примером выражения W, полученного заменой всех вхождений в W переменной xi (1 i n), на вхождение терма ti. W будет называться фундаментальным примером выражения W, если – фундаментальная подстановка.
Слайд 16Унификация
Главная цель поиска подходящих подстановок – сделать две литеры идентичными,
чтобы затем использовать их как контрарную пару при выводе нового
дизъюнкта.
Подстановка называется унификатором, если для выражений {W1, W2} справедливо W1 = W2.
Если для выражений множества {W1, W2} имеется унификатор, скажем, что множество унифицируемо.
Очевидно, можно придумать не единственную систему подстановок, с помощью которых две литеры могут стать идентичными. Самая короткая система подстановок (наиболее «экономная») из возможных, называется наиболее общим унификатором (НОУ).
Существует алгоритм нахождения НОУ. Этот алгоритм за конечное число шагов находит НОУ для предъявленных выражений, либо сообщает, что множество не унифицируемо.
Слайд 17Получение резольвенты для ИП
Пусть С1 и С2 – два дизъюнкта,
не имеющие общих переменных (это всегда можно получить переименованием переменных).
И пусть L1 и L2 = L1 – литеры в дизъюнктах С1 и С2 соответственно, имеющие НОУ . Тогда бинарной резольвентой для С1 и С2 является дизъюнкт вида
C = (C1 - L1) (C2 - L2).
Бинарная резольвента может быть получена одним из четырех способов:
резольвента для С1 и С2;
резольвента для С1 и дизъюнкта С2, к которому применена подстановка;
резольвента для дизъюнкта С1 к которому применена подстановка, и С2;
резольвента для дизъюнкта С1 и дизъюнкта С2 к которым применена подстановка.
Слайд 18Пример получения резольвенты.
Пусть имеются два дизъюнкта:
C1= P(f(g(a))) R(b),
C2 = P(x) P(f(y)) Q(y).
Чтобы унифицировать два
выделенных выражения, используем подстановку = {g(a)/y}
Тогда C2 = C2 = P(x) P(f(g(a))) Q(g(a))
и резольвентой для С1 и С2 будет С = P(x) R(b) Q(g(a)) ( = g(a)/y).
Теорема. (Теорема о полноте Дж. Робинсона). Множество дизъюнктов S невыполнимо тогда и только тогда, когда существует вывод методом резолюции из S пустого дизъюнкта.
Слайд 19Пример решения задачи
Рассмотрим задачу.
Каждый молодой человек занимается спортом. Некоторые
молодые люди являются студентами. Следовательно, существуют студенты – спортсмены.
Формальная запись
рассуждения:
x (М(x) S(x))
x (М(х) & C(x))
--------------------
x (C(х) & S(x))
Преобразование каждой посылки и отрицания заключения позволило нам получить следующие дизъюнкты:
M(x) S(x)
(2) М(с)
(3) C(с)
(4) С(x) S(x)
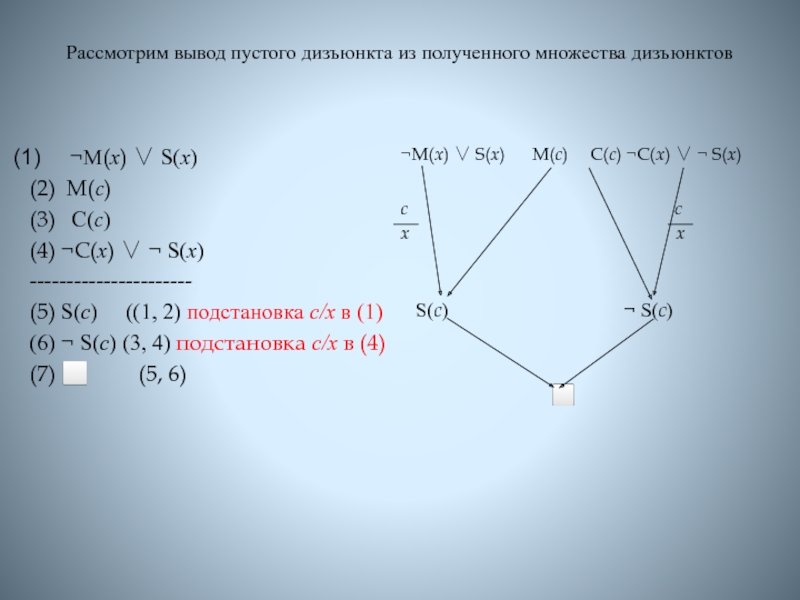
Слайд 20Рассмотрим вывод пустого дизъюнкта из полученного множества дизъюнктов
M(x) S(x)
(2)
М(с)
(3) C(с)
(4) С(x) S(x)
----------------------
(5) S(с)
((1, 2) подстановка c/x в (1)
(6) S(с) (3, 4) подстановка c/x в (4)
(7) (5, 6)
M(x) S(x) М(с) C(с) С(x) S(x)
с с
х х
S(с) S(с)
Слайд 211. Формализация
Рассмотрим более сложную задачу.
«Некоторые студенты любят всех преподавателей. Ни
один из студентов не любит невежд. Следовательно, ни один из
преподавателей не является невеждой.»
Введём предикаты С(х) «х – студент»,
Р(х) «х – преподаватель»,
N(x) «х- невежда»,
L(x, y) «х любит y - ка».
Посылка 1: x (C(x) & y(P(y) L(x, y)))
Посылка 2: x (C(x) y(N(y) L(x, y)))
Заключение: y (P(y) N(y)).
Слайд 222. Получение дизъюнктов
(Р1) x (C(x) & y(P(y)
L(x, y))) = x (C(x) & y(P(y) L(x, y))) =
= x y (C(x) & (P(y) L(x, y))) ПНФ
Приводим Р1 к ССФ. Квантор x находится на первом месте, вычеркиваем его, заменяя х на константу а.
y (C(а) & (P(y) L(а, y)) - ССФ.
Получили два дизъюнкта: C(а), P(y) L(а, y)
(Р2) x (C(x)y(N(y) L(x, y))) = x(C(x) y(N(y)L(x, y)))=
= xy (C(x) N(y)L(x, y)) ПНФ = ССФ (нет кванторов -я).
Получаем дизъюнкт C(x) N(y)L(x, y)
Отрицание заключения y (P(y) N(y)) = y (P(y) N(y)) =
= y ( P(y) N(y)) = y (P(y) &N(y)) – ПНФ
Приводим к ССФ. Квантор y находится на первом месте, вычеркиваем его, заменяя y на константу b. Получаем два дизъюнкта P(b) , N(b)) .
Слайд 233. Вывод пустого дизъюнкта
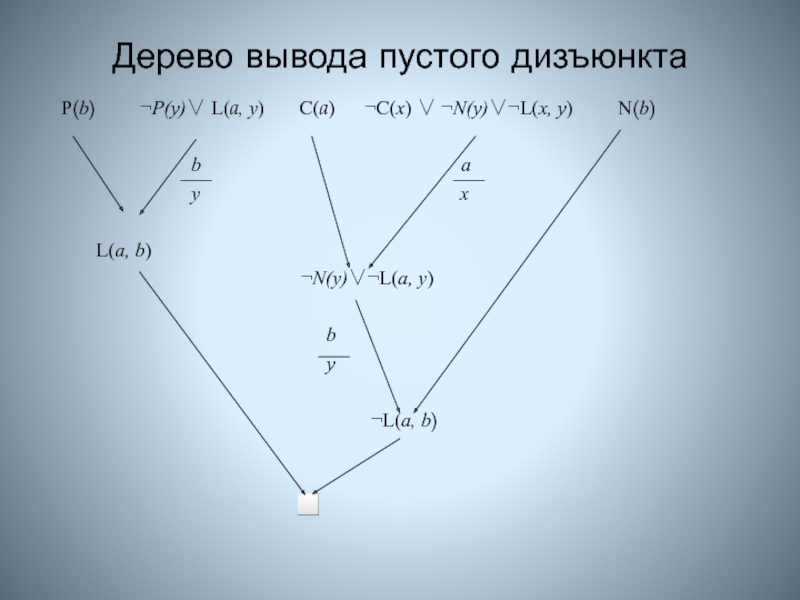
Множество S содержит дизъюнкты:
C(а)
P(y) L(а, y)
C(x)
N(y)L(x, y)
P(b)
N(b)
------------
(6) L(a, b)
(2,4), подстановка {b/y} в дизъюнкт 2
(7) N(y)L(a, y) (1, 3) подстановка {a/x} в дизъюнкт 3
(8) L(a, b) (5,7) подстановка {b/y} в дизъюнкт 7
(9) (6, 8)
Слайд 24Дерево вывода пустого дизъюнкта
P(b) P(y) L(а,
y) C(а) C(x) N(y)L(x,
y) N(b)
b a
y x
L(a, b)
N(y)L(a, y)
b
y
L(a, b)