Слайд 1Дискретные системы
Дискретные АСУ - системы, в состав которых, помимо типовых
динамических звеньев, входят одно или несколько звеньев, производящих квантование непрерывного
сигнала в дискретный.
Дискретные АСУ делятся на:
импульсные,
релейные
цифровые.
Квантование сигнала осуществляется в импульсных АСУ - по времени, в релейных -по уровню, в цифровых -по времени и по уровню.
Слайд 2
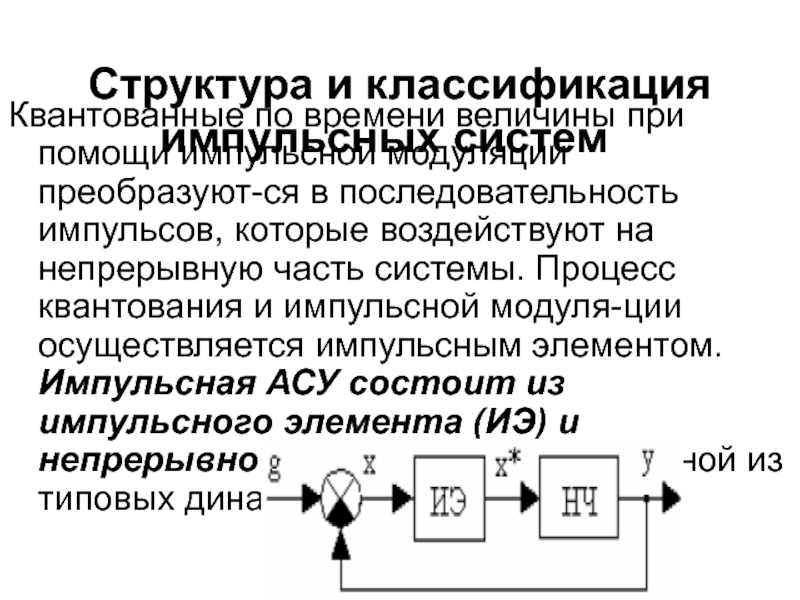
Структура и классификация импульсных систем
Квантованные по времени величины при
помощи импульсной модуляции преобразуют-ся в последовательность импульсов, которые воздействуют на
непрерывную часть системы. Процесс квантования и импульсной модуля-ции осуществляется импульсным элементом. Импульсная АСУ состоит из импульсного элемента (ИЭ) и непрерывной части (НЧ), составленной из типовых динамических звеньев.
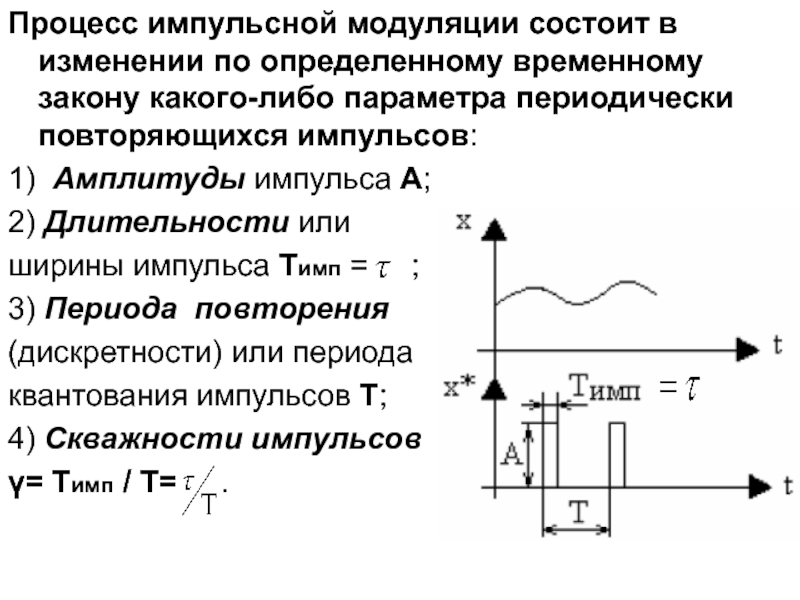
Слайд 3Процесс импульсной модуляции состоит в изменении по определенному временному закону
какого-либо параметра периодически повторяющихся импульсов:
1) Амплитуды импульса А;
2) Длительности
или
ширины импульса Тимп = ;
3) Периода повторения
(дискретности) или периода
квантования импульсов Т;
4) Скважности импульсов
γ= Тимп / Т= .
Слайд 4Виды импульсной модуляции
1) амплитудно-импульсная модуляция - АИМ (амплитуда импульса пропорциональна
входному сигналу: A = f(x) при T = const, Тимп
= const);
2) широтно-импульсная модуляция - ШИМ (длительность импульса пропорциональна входному сигналу: Тимп = f(x) при A = const, T = const);
3) временная импульсная модуляция - ВИМ, включающая в себя:
фазо-импульсную модуляцию - ФИМ (фаза, т.е. временной сдвиг импульса относительно начала периода дискретности T, пропорциональна входному сигналу:
ϕ = f(x) при A = const, T = const, Тимп = const);
частотно-импульсную модуляцию -ЧИМ (частота дискретности пропорциональна входному сигналу:
ω0 = f(x) при A = const, Тимп = const).
Величина, определяющая закон модуляции, называется модулирующей величиной.
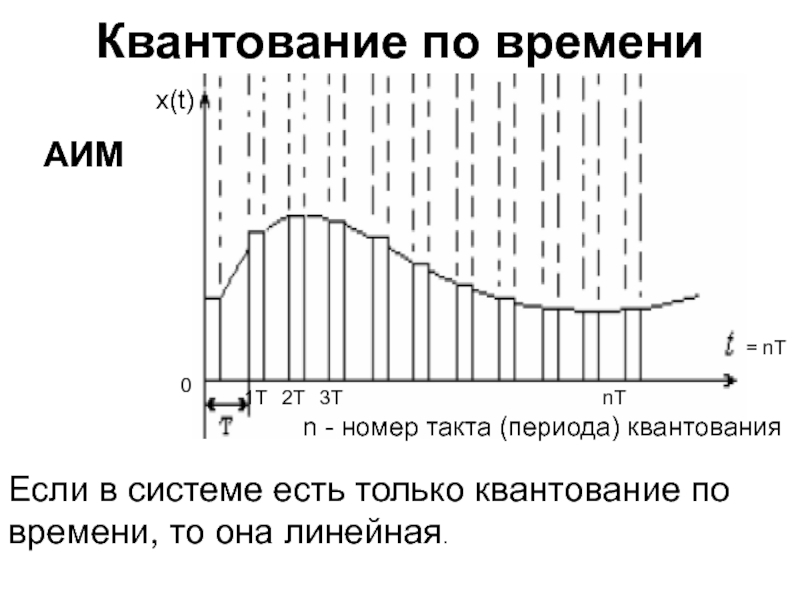
Слайд 5Квантование по времени
x(t)
0
1T
2T
3T
nT
= nT
Если в системе есть только квантование по
времени, то она линейная.
АИМ
n - номер такта (периода) квантования
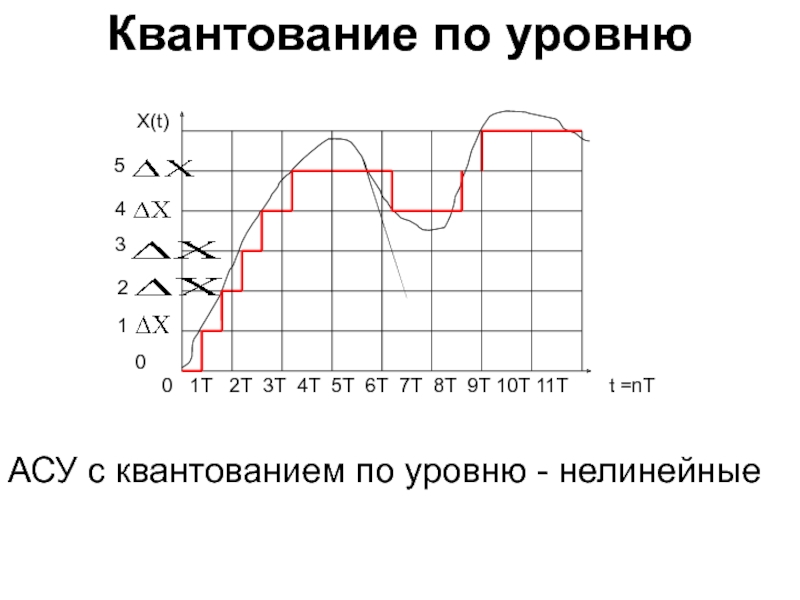
Слайд 6Квантование по уровню
АСУ с квантованием по уровню - нелинейные
X(t)
t =nT
2
3
4
5
1
0
0
1T 2T 3T 4T 5T 6T 7T 8T
9T 10T 11T
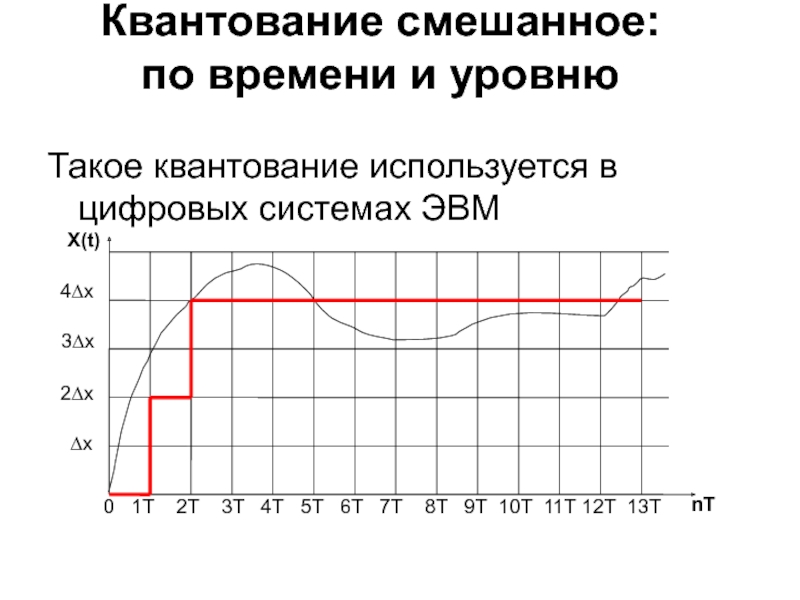
Слайд 7Квантование смешанное:
по времени и уровню
Такое квантование используется в цифровых
системах ЭВМ
X(t)
nT
0 1T 2T 3T 4T
5T 6T 7T 8T 9T 10T 11T 12T 13T
4∆x
2∆x
∆x
3∆x
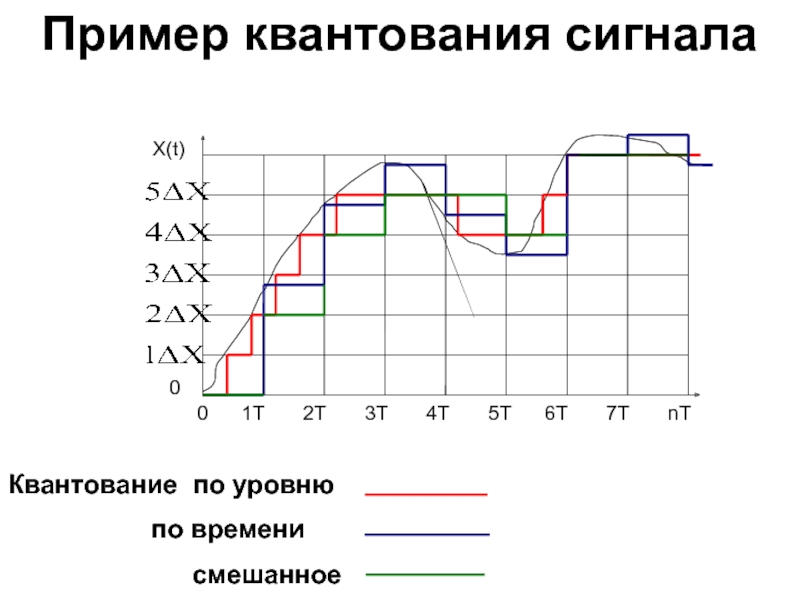
Слайд 8Пример квантования сигнала
0 1T 2T
3T 4T
5T 6T 7T nT
X(t)
0
Квантование по уровню
по времени
смешанное
Слайд 9Достоинства импульсных АСУ
Возможность управления большими мощностями с высокой точностью;
Возможность разделения
во времени информационных сигналов при многоканальной передаче (ТП);
Обеспечение согласованной работы
непрерывных устройств с ЦВМ;
Повышенная помехозащищенность.
Слайд 10
Математическое описание дискретных систем
Дискретные АСУ удобно описывать функцией дискретной
переменной, когда все величины рассматриваются в дискретные равноотстоящие моменты времени
- решетчатой функцией (РФ) и разностным уравнением.
Решетчатая функция времени x[nT], или в сокра-щенной записи x[n] - это математическая функция, значения которой определены в дискретные равно-отстоящие друг от друга моменты времени t = nT,
где n -целое положительное число 0, 1, 2 ...;
Т - период дискретности (квантования).
Слайд 11РФ представляет собой числовую последовательность:
x[0], x[1T], x[2T], x[3T], ...
,x[nT], ... .
Если период дискретности T
задан, то РФ однозначно
формируется из исходной
непрерывной. Операция
замены непрерывной
функции решетчатой
x[nT] = x[n] = x(t)
t = nT
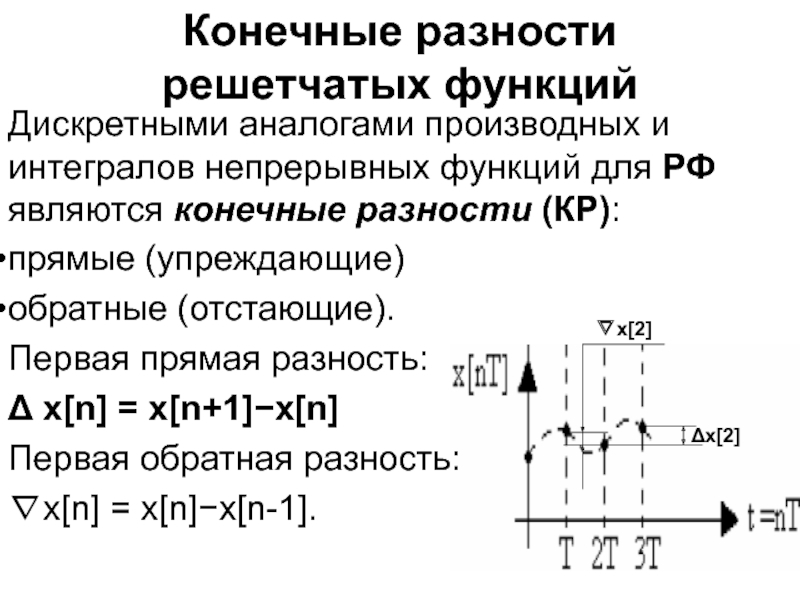
Слайд 12Конечные разности решетчатых функций
Дискретными аналогами производных и интегралов непрерывных функций
для РФ являются конечные разности (КР):
прямые (упреждающие)
обратные (отстающие).
Первая прямая разность:
Δ x[n] = x[n+1]−x[n]
Первая обратная разность:
∇x[n] = x[n]−x[n-1].
Δx[2]
∇x[2]
Слайд 13Разности произвольного порядка k определяются по рекуррентным соотношениям:
Δk x[n] = Δ{Δk-1 x[n]} = Δk-1 x[n+1] − Δk-1
x[n]=
k
= ∑ (-1) x[n+k - ], (*)
∇k x[n] = ∇{∇k-1 x[n]} = ∇k-1 x[n] − ∇k-1 x[n-1]=
k
= ∑ (-1) x[n- ],
Слайд 14Непрерывные АСУ Дискретные АСУ
x(t)
x[nT] или x[n]
dx
dt Δx[nT] или Δx[n]
dkx Δkx[nT] или Δkx[n]
dtk
неполная сумма
nT (n+1)T nT
x[nT]
или полная сумма
Слайд 15Разностные уравнения
Разностные уравнения (РУ) - (уравнения в конечных разностях) связывают
между собой решетчатые функции и их конечные разности. РУ -
аналоги дифференциальных уравнений, описывающих непрерывные АСУ.
При использовании прямых разностей неоднородные линейные РУ m-го порядка имеют вид:
Слайд 16РУ при использовании (*) можно записать через значения решетчатой функции:
При х[n] = 0 это уравнение становится однородным РУ, решением
которого будет y[n].
Общее решение однородного РУ при некратных корнях характеристического уравнения может быть записано:
где Ci -постоянные коэффициенты;
zi -корни характеристического уравнения:
Слайд 17Задача формирования непрерывной функции из РФ не может быть решена
однозначно без дополнительных сведений о поведении функции в интервале между
точками t = nT, т.к. РФ, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.
Возникает вопрос, при
каких условиях возможно
точное восстановление
квантованной функции.
Ответ на него дает теорема Котельникова-Шеннона.
x[nT]
0 nT (n+1)T nT
x[nT]
x[(n+1)T]
Слайд 18Теорема Котельникова-Шеннона:
непрерывный сигнал x(t), частотный спектр которого ограничен полосой 0
< fs< fс, полностью определяется последователь-ностью своих дискретных значений, если
период квантования Т удовлетворяет условию: Т < 1 /2fс или Т < π /ωс ,
где fс[Гц], ωс [с-1] - частота спектра.
Частота квантования: ω 2ωс При выполнении этого условия потери информации не происходит и из квантованного сигнала можно без потерь восстановить исходный непрерывный сигнал.
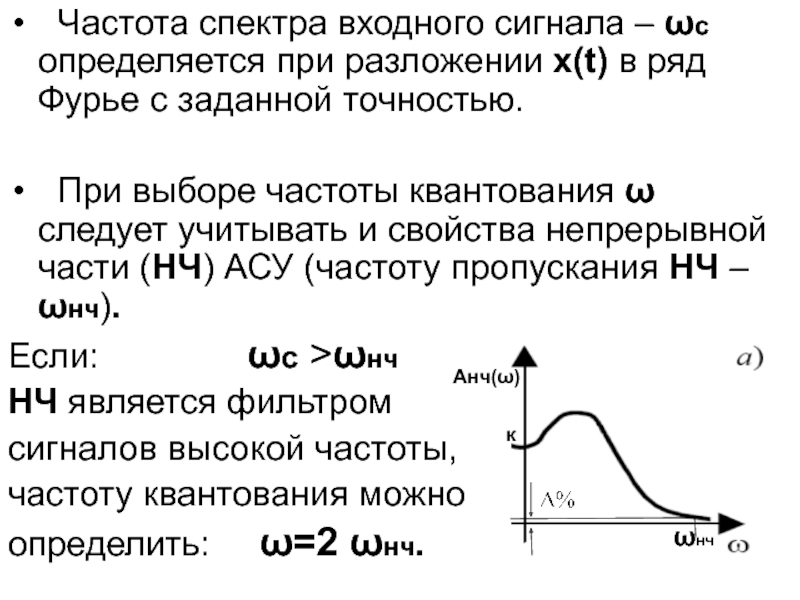
Слайд 19 Частота спектра входного сигнала – ωс определяется при разложении
x(t) в ряд Фурье с заданной точностью.
При выборе частоты
квантования ω следует учитывать и свойства непрерывной части (НЧ) АСУ (частоту пропускания НЧ – ωнч).
Если: ωс >ωнч
НЧ является фильтром
сигналов высокой частоты,
частоту квантования можно
определить: ω=2 ωнч.
Анч(ω)
ωнч
к
Слайд 20Методы исследования дискретных АСУ
Для получения возможности исследования решений РУ в
общем виде широко используются:
дискретное преобразование Лапласа,
z-преобразование,
w-преобразование,
частотные методы.
Слайд 21
Z -преобразование
Z-преобразованием РФ - x[nT] называется функция комплексного аргумента
z - X(z) , определяемая выражением:
при z > R=1/ρ ,
где ρ -радиус сходимости ряда. Функция x[nT] - оригинал,
а функция X(z) - изображение или
z-преобразование функции x[nT].
Z-преобразование дает возможность получить из X(z) значение ординат РФ - x[nT] в моменты квантования.
Слайд 22
Z - преобразования функций времени
Для нахождения z-изображений РФ по
оригиналу и наоборот имеются специальные таблицы.
Преобразование, в котором
введено Я.З.Цыпкиным
под названием “дискретное преобразование Лапласа”.
Слайд 23Вычисление Z-преобразований
Способ 1:
(по определению) Пример:z- изображение ступенчатой функции
x(t)=A*1(t)
X(t)
t
A
t
Слайд 24Способ 2 : (с помощью вычетов)
Если известно преобразование Лапласа X(s) исходной
непрерывной функции x(t), то можно вычислить Z -преобразование X(z):
x(t)
квантование x[nT]
Z –преобра- зование
X(s) переход к Z -преобразованию X(z)
sk – полюса (простые) преобразования Лапласа X(s) непрерывной функции x(t).
В случае кратных корней формула усложняется (можно найти в справочниках).
Пример: x(t) = 1(t); X(s) = 1/s. Вычисляем с помощью таблиц справочника:
Слайд 25
Свойства z-преобразования
Свойство линейности: изображению линейной комбинации РФ
соответствует такая же линейная комбинация
z-изображений:
Свойство смещения аргумента в области оригинала: сдвиг аргумента [nT] в РФ на целое число периодов соответствует умножению изображения X(z) на :
Слайд 263. Свойство смещения независимой переменной в области изображения : сдвигу
аргумента в z- изображении на целое число периодов в комплексной
области соответствует умножение z на
4. Правило дифференцирования изображения: умножение РФ на nT соответствует дифференцированию ее
z- изображения X(z), результат которого умножается на (-Tz):
Слайд 275. Связь начальных и конечных значений: начальное значение оригинала РФ
равно конечному значению z- изображения :
Конечное значение РФ:
6. Изображение разностей:
Слайд 28Тренировочное задание
Прямая конечная разность 2-го порядка:
Слайд 29Передаточная функция импульсной АСУ в
z- изображении
Разностное уравнение (РУ) АСУ:
Выполнив
z – преобразование РУ, получим передаточную функцию АСУ в z-изображении:
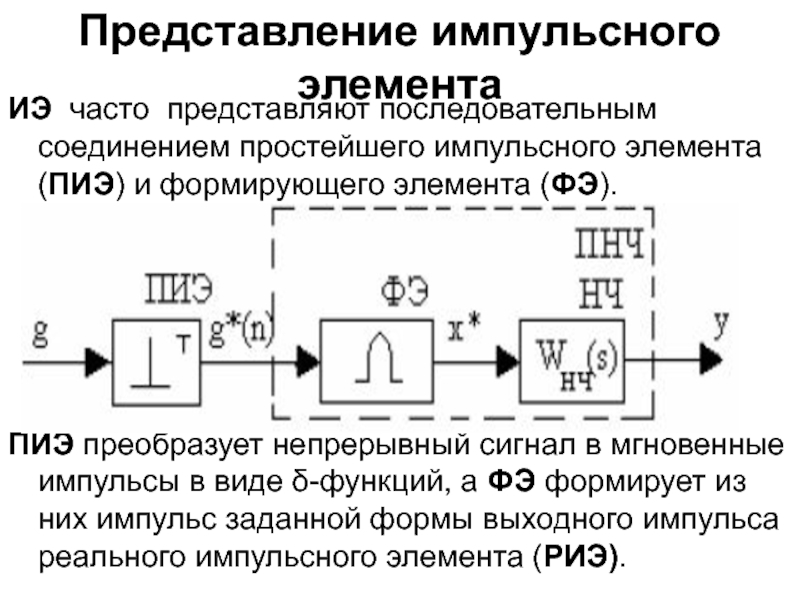
Слайд 30Представление импульсного элемента
ИЭ часто представляют последовательным соединением простейшего импульсного элемента
(ПИЭ) и формирующего элемента (ФЭ).
ПИЭ преобразует непрерывный сигнал в
мгновенные импульсы в виде δ-функций, а ФЭ формирует из них импульс заданной формы выходного импульса реального импульсного элемента (РИЭ).
Слайд 31Передаточная функция ФЭ
На выходе ПИЭ ширина импульса : → 0;
Действие ПИЭ сводится к умножению отсчётов квантуемой функции x(t) на дельта- функцию δ(t-nТ). Форма импульса РИЭ определяет весовую функцию ФЭ - kФЭ(t). Поэтому, передаточную функцию ФЭ определим как изображение формы импульса по Лапласу, т.е.
WФЭ(s)=L {kФЭ(t)}.
ФЭ объединяется с непрерывной частью (НЧ) АСУ в приведенную непрерывную часть (ПНЧ), передаточная функция которой
WПНЧ(s) = WФЭ(s)*WНЧ(s).
Слайд 32В большинстве случаев РИЭ формирует
прямоугольные импульсы
длительности Tимп =
γТ= ,
т.е. весовая функция ФЭ имеет
вид:
Kфэ(t)
В этом случае передаточная функция ФЭ:
WФЭ(s)
Отсюда: Это экстраполятор нулевого WФЭ(s) порядка.
Порядок экстраполятора определяется порядком производной от формы импульса на интервале
k
Слайд 33Передаточные функции типовых импульсов
Треугольный импульс
Синусоидальный импульс
Экспоненциальный импульс
x(t)
x(t)
x(t)
t
t
t
T
T
T
T
Слайд 34Определение передаточной функции Wпнч(s)
Рассмотрим при наличии формирователя прямоугольных импульсов:
Wпнч(s)= WФЭ(s)*WНЧ(s) WНЧ(s)=
.
Переходя от непрерывного преобразования Лапласа
к z-преобразованию: Wпнч(z)= .
Выражение
необходимо представить как сумму элементарных дробей (например, по теореме разложения, используя метод неопределенных коэффициентов ), а затем выполнить z-преобразование каждой из дробей (справочник).
нч
нч
нч
Слайд 35Теорема разложения
- коэффициенты разложения, определяются:
методом неопределенных коэффициентов;
методом
предельных значений;
методом подстановки численных значений.
Слайд 36Тренировочное задание
Пример. Определить дискретную передаточную функцию импульсной АСУ, у которой
ИЭ формирует прямоугольные импульсы длительности = 1с периодом дискретности
T=1 c, а непрерывная часть задана передаточной функцией:
Слайд 37
Р е ш е н и е
Дискретную передаточную функцию
разомкнутой импульсной системы находим, представляя дробь
в виде суммы элементарных дробей:
нч
нч
=
Слайд 38С помощью таблицы соответствий найдем
z-преобразование для каждого из слагаемых
в
правой части полученного выражения:
при форми- ровании прямоугольных импульсов:
нч
нч
пнч
р
Слайд 39
Структурные схемы и передаточные функции замкнутых дискретных АСУ
ПНЧ
Изображение РФ
- y[n] Y(z) = W(z) X(z)
W(z) = Z{WФЭ(s)W1(s)W2(s)}.
Уравнение
z-изображения
рассогласования:
Тогда z-изображение выходной координаты:
Y(z) = {W(z) /[1+ W(z) ]} G(z)
Слайд 40Передаточная функция замкнутой АСУ
пр
р
фэ
нч.пр
фэ
нч.р
пнч.пр
пнч.р
Слайд 41Частотные характеристики импульсных систем
Выражения для ЧХ импульсных систем получаются из
W(z) путем замены оператора z на
.
Т.к. частота ω входит в показатель степени, то ЧХ являются периодическими функциями частоты, период изменения которых равен ±π/ ω или (2π/ ω).
Следовательно, нельзя различить составляющие, частоты которых кратны частоте квантования импульсного элемента ωо = 2π/Т.
Слайд 42
ЧХ импульсных систем описываются трансцендентными выражениями:
A(ω) = mod W(
) - АЧХ;
ψ(ω) = arg W(
) - ФЧХ;
U(ω) = Re W( ) - ВЧХ;
V(ω) = Im W( ) - МЧХ;
W( ) = W(z) - АФЧХ.
z =
ЧХ импульсной АСУ строятся по точкам в интервале частот 0 ≤ ω ≤ π⁄ Т.
Слайд 43Свойства ЧХ импульсных АСУ
1. В соответствии с периодичностью АФЧХ
W( ) полностью определяется своими значениями в
интервале −π⁄ Т ≤ ω ≤ π⁄ Т.
2. Т.к. ВЧХ является четной функцией, а МЧХ - нечетной, то достаточно рассматривать интервал частот 0 ≤ω ≤ π⁄ Т.
3. В крайних точках интервала 0 ≤ ω ≤ π⁄ Т АФЧХ принимает вещественные значения.
4. При уменьшении периода дискретности T, т.е. при увеличении частоты квантования ω0 = 2π/Т,
ЧХ импульсных АСУ приближаются к ЧХ непрерывных систем, а частотный интервал 0 ≤ ω ≤ π⁄ Т растягивается на всю ось ω при T → 0.
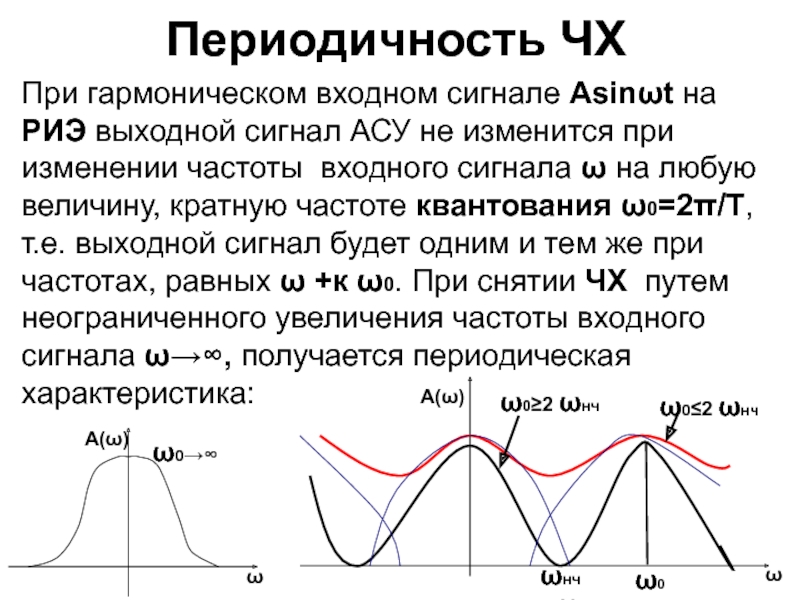
Слайд 44Периодичность ЧХ
При гармоническом входном сигнале Аsinωt на РИЭ выходной сигнал
АСУ не изменится при изменении частоты входного сигнала ω на
любую величину, кратную частоте квантования ω0=2π/Т, т.е. выходной сигнал будет одним и тем же при частотах, равных ω +к ω0. При снятии ЧХ путем неограниченного увеличения частоты входного сигнала ω→∞, получается периодическая характеристика:
А(ω)
ω
ω
ωнч
ω0
ω0≥2 ωнч
ω0≤2 ωнч
ω
А(ω)
ω0→∞
Слайд 45W- преобразование
Определение ЧХ связано со сложными расчетами, поэтому на практике
применяются ЧХ относительно абсолютной псевдочастоты λ. Переход к псевдочастоте основан
на переходе от
z-преобразования к
w-преобразованию
с помощью подстановки:
c последующей заменой комплексной переменной w на абсолютную псевдочастоту:
Такая замена и есть
w –преобразование.
Слайд 46Реальная частота ω и псевдочастота λ связаны соотношением
Удобство псевдочастоты в
том, что на частотах, где ωT < 2, она приближенно
равна угловой частоте, т.е. λ ≈ ω. При изменении частоты от −π⁄ Т <ω <+π⁄ Т псевдочастота принимает значение −∞ <λ< +∞.
Для перехода от дискретной передаточной функции разомкнутой АСУ Wр (z) к АФЧХ - Wр (jλ) сделаем замену
Это уравнение используется для построения ЛАЧХ.
Слайд 47Построение ЛЧХ импульсных АСУ
ЛАЧХ строятся отдельно для областей низких (НЧ)
и высоких частот (ВЧ). Границей, разделяющей частотные области, служит частота
среза ωср в предположении, что
ωср* T< 2 ,
где Т - период дискретности.
Это условие необходимо выполнять для обеспечения запаса устойчивости и точности работы системы, и оно согласуется с теоремой Котельникова-Шеннона.
Слайд 48Построим ЛАЧХ АИС, с экстраполятором нулевого порядка и непрерывной
частью с передаточной функцией:
нч
Слайд 49Принятые допущения:
1. Величина, обратная периоду дискретности T, больше половины частоты
среза ωср, т.е. ωср < 2/T.
2. На частоте среза ЛАЧХ
непрерывной части имеет наклон −20 дБ/дек.
3. Постоянным времени Тj (j = 1, 2, ..., m) соответствуют частоты сопряжения меньшие, чем частота среза ωсj < ωср.
4. Имеется l(l< n) постоянных времени Ti (i = 1, 2,..., l), которым соответствуют сопрягающие частоты меньшие, чем частота среза.
Слайд 50При принятых допущениях для области низких частот передаточная функция непрерывной
части:
а для области высоких частот;
нч
нч
н
в
Слайд 51Wфэ(s)Wнч (s)→Wпнч (z) = z{Wфэ(s)Wнч(s)} → →W(jλ)
ЧХ разомкнутой
импульсной АСУ для области низких частот:
и для области высоких частот:
Слайд 52Выводы:
В НЧ области АФЧХ импульсной АСУ получим из Wнч (s)
подстановкой s = jλ и умножением на множитель (1 −
jλT/2). В этой области λ ≈ω. Влиянием дополнительного множителя в НЧ области можно пренебречь, т.к. ωср < 2/T.
В области низких частот ЧХ импульсной АСУ совпадают с ЧХ ее непрерывной части.
Начало ЛАЧХ в ВЧ области совпадает с концом ЛАЧХ, построенной в НЧ области.
Слайд 53Выражение результирующей АФЧХ разомкнутой АИС представляет собой произведение элементарных типовых
сомножителей, его легко использовать для построения ЛАЧХ импульсных АСУ.
Результирующий
фазовый сдвиг:
Слайд 54Пример. Построить ЛАЧХ АИС с
экстраполятором нулевого порядка и периодом дискретности
ИЭ T = 4 с, передаточная функция непрерывной части:
Слайд 55Р е ш е н и е
Выбираем частоту среза ωcр
< 2/T < 0.5 c-1. В соответствии с заданными постоянными
времени определяем сопрягающие частоты:
ωc1=1/25=0.04 c-1 – НЧ диапазон;
ωc2=1/0.5=2 c-1 - ВЧ диапазон;
ωc3=1/0.3=3.33 c-1 – ВЧ диапазон.
Следовательно, получаем:
Слайд 56
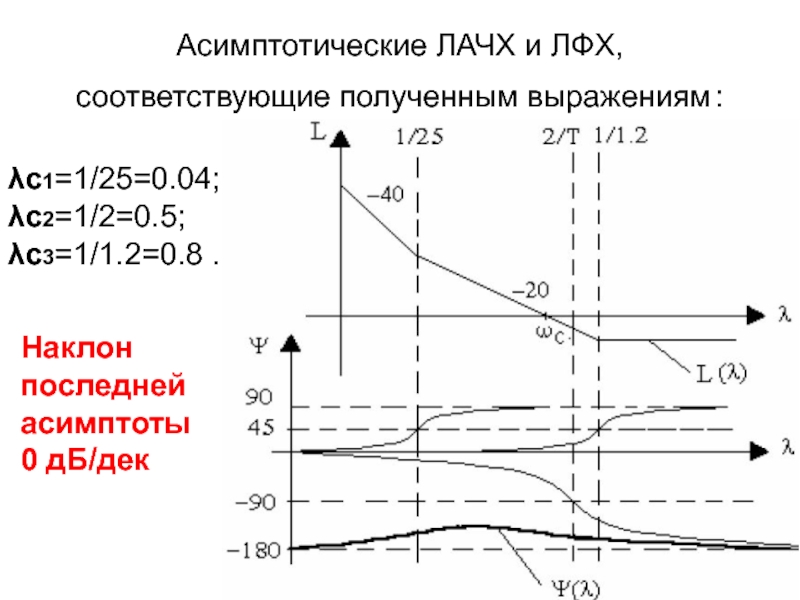
Асимптотические ЛАЧХ и ЛФХ, соответствующие полученным выражениям :
λс1=1/25=0.04;
λс2=1/2=0.5;
λс3=1/1.2=0.8 .
Наклон последней асимптоты
0 дБ/дек
Слайд 57
Устойчивость импульсных АСУ
Линейная импульсная АСУ устойчива, если свободная составляющая
переходного процесса yп[n] затухает с течением времени: .
Она
определяется решением однородного РУ замкнутой импульсной АСУ
a0y[n] + a1y[n−1] + ... + amy[n−m] = 0,
где m - порядок системы.
При некратных корнях характеристического уравнения:
где zi - корни характеристического уравнения
Слайд 58Для устойчивости импульсной АСУ необходимо и достаточно, чтобы все корни
характеристического полинома удовлетворяли условию
i =
1, 2, ..., m.
Если хотя бы один корень , система будет неустойчивой. Значение корня при всех остальных
определяет границу устойчивости АСУ.
Графически область устойчивости на плоскости z корней характеристического уравнения изображается
единичным кругом.
Области устойчивости
на плоскости Z
Исследование устойчивости сводится к изучению расположе-ния корней характеристического полинома замкнутой импульсной АСУ относительно единичной окружности.
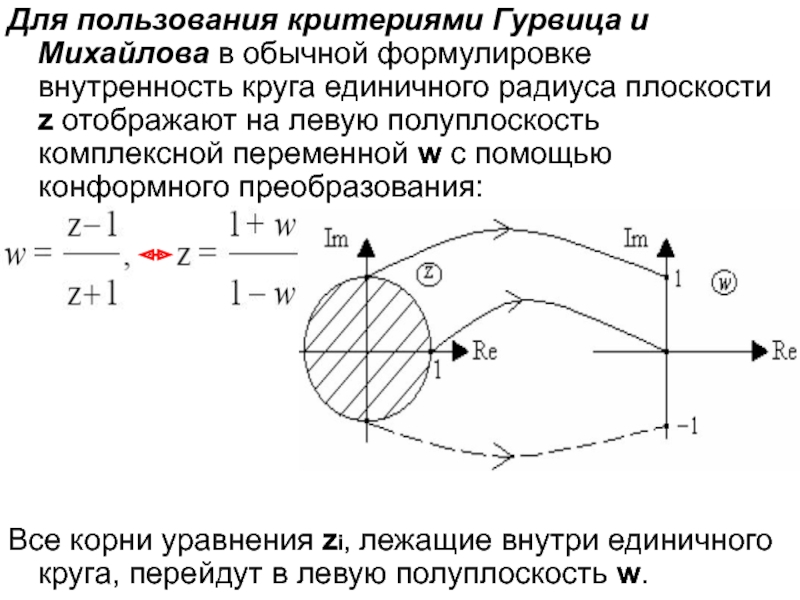
Слайд 59Для пользования критериями Гурвица и Михайлова в обычной формулировке внутренность
круга единичного радиуса плоскости z отображают на левую полуплоскость комплексной
переменной w с помощью конформного преобразования:
Все корни уравнения zi, лежащие внутри единичного круга, перейдут в левую полуплоскость w.
Слайд 60После подстановки
в характеристическое уравнение
получим:
Преобразованное характеристическое уравнение импульсной АСУ:
При использовании
этого уравнения для устойчивости импульсной АСУ необходимо и достаточно, чтобы все корни wi (i = 1, 2, ..., m) имели отрицательные вещественные части. Границей устойчивости служит мнимая ось.
Для анализа устойчивости импульсных АСУ могут применять-ся также ЛАЧХ в формулировке для непрерывных АСУ.
Слайд 61Критерии устойчивости
используются для исследования устойчивости импульсных АСУ без нахождения корней
характеристического уравнения.
Аналог критерия Рауса-Гурвица. Wз (z)→Wз (w)
Степень характерис- Условия
устойчивости
тического уравнения
Используется характеристи-ческий полином, полученный после
W-преобразо-вания Wз (w)
Слайд 62Аналог критерия Михайлова
Для устойчивости линейной импульсной АСУ m-го порядка необходимо
и достаточно, чтобы изменение аргумента функции
при изменении частоты ω от 0 до π/T равнялось бы значению mπ , то есть
Δ arg = mπ , 0 ≤ ω ≤ π/T.
Здесь получается путем замены z на в характеристическом полиноме замкнутой АСУ
, z = .
На рис. аналоги
кривых Михайлова для
устойчивой и неустойчивой
импульсной АСУ при m = 3.
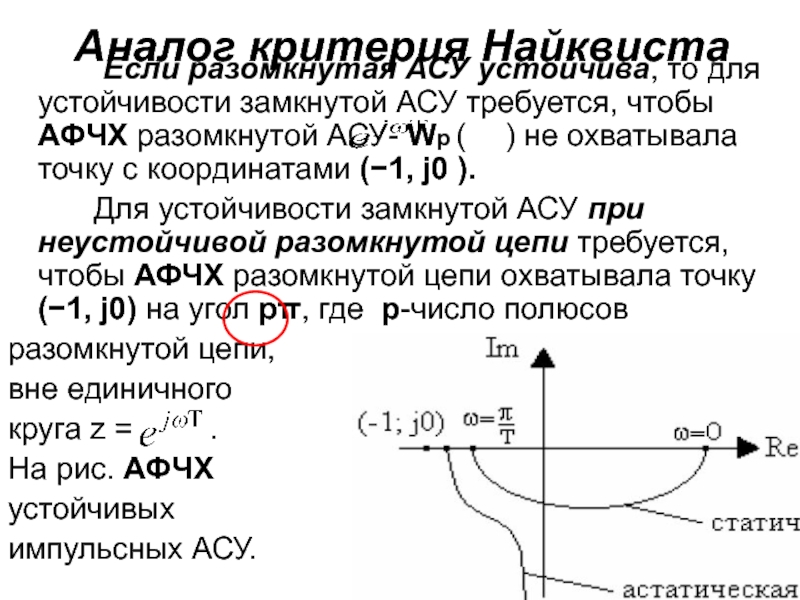
Слайд 63Аналог критерия Найквиста
Если разомкнутая
АСУ устойчива, то для устойчивости замкнутой АСУ требуется, чтобы АФЧХ
разомкнутой АСУ- Wр ( ) не охватывала точку с координатами (−1, j0 ).
Для устойчивости замкнутой АСУ при неустойчивой разомкнутой цепи требуется, чтобы АФЧХ разомкнутой цепи охватывала точку (−1, j0) на угол pπ, где p-число полюсов
разомкнутой цепи,
вне единичного
круга z = .
На рис. АФЧХ
устойчивых
импульсных АСУ.
Слайд 64Точность импульсных АСУ
Установившаяся ошибка импульсной АСУ опреде-ляется по предельному значению
решетчатой функции:
Слайд 65Установившиеся ошибки
установившаяся ошибка пропорциональна величине задающего воздействия и периоду
дискретности.
{
Слайд 66Астатизм АСУ
Представим передаточную функцию импульсной разомкнутой АСУ
при r = 0
АСУ статическая,
при r = 1 - астатическая первого
порядка и т.д., и
W(1)→ ∞.
от задающего воздействия, если степень астатизма r
превышает степень
полинома k входного
воздействия.
Слайд 67Сигнал ошибки при непрерывном входном сигнале
коэффициенты ошибок.
Слайд 68Сигнал ошибки при дискретном входном сигнале
Слайд 69Переходные процессы в импульсных АСУ
определяются с помощью :
обратного z-преобразования,
ряда Лорана,
решения разностного уравнения,
частотных методов, основанных на использовании ВЧХ или МЧХ замкнутой АСУ.
Слайд 70Обратное z-преобразование
Для расчета переходного процесса можно найти обратное z-преобразование изображения
выходной величины АСУ
,используя формулу обращения, согласно которой
где zi - полюсы выражения Y(z); i = 1, 2, ..., k.
Вычет в простом полюсе:
в полюсе кратности r:
Слайд 71Из определения z-преобразования:
– дробно-рациональная функция.
- для
простых полюсов zi.
корни характеристического уравнения A(z)=0;
общее количество корней;
производная полинома
A(z) по z.
Слайд 72Разложение изображения Y(z) в ряд Лорана
Дискретные значения переходного процесса можно
найти путем разложения Y(z) в ряд Лорана по степеням
:
Коэффициенты определяют выходную величину АСУ в дискретные моменты времени t =nT.
Y(z) представляет собой отношение двух полиномов, поэтому коэффициенты ряда Y0, Y1, Y2, ... можно получить делением полинома числителя на полином знаменателя.
При Т→0 ряд сходится медленно и объем вычислительной работы значителен.
Слайд 73Вычисление коэффициентов ряда Лорана
Z- изображение выходной координаты:
Слайд 74Коэффициенты разложения в ряд Лорана:
1
Слайд 75Метод разностного уравнения
Дискретная АСУ представлена передаточной
функцией:
Слайд 76Разностное уравнение в этом случае:
Решение уравнения:
2
Слайд 77Рекуррентные зависимости 1 и 2 используются и для
расчета переходных процессов в непрерывных АСУ после дискретизации их дифференциальных
уравнений.
Слайд 78Коррекция импульсных систем
КУ обеспечивают заданные требования по точности и по
качеству процесса управления, исходя из которых составляются желаемые характеристики АСУ.
Для коррекции импульсных АСУ имеется большее разнообразие технических средств, чем для непрерывных АСУ, т.к. кроме непрерывных КУ можно вводить импульсные и цифровые.
Находит применение:
Непрерывная коррекция;
Импульсная коррекция.
Слайд 79Непрерывная коррекция
В этом случае изменяют характеристики непрерывной части АСУ введением
последовательных или параллельных КУ,
местной отрицательной или положительной
обратной связи.
При расчете непрерывных КУ целесообразно перейти от желаемой характеристики импульсной АСУ к желаемой характеристике ее непрерывной части. Задача синтеза решается так же, как она решалась для обыкновенных линейных АСУ.
Слайд 80Импульсная коррекция
выполняется введением в АСУ импульсного фильтра. Он преобразует входной
сигнал x(t) в последовательность импульсов
сформированных путем амплитудно-импульсной модуляции x(t) с
необходимыми для коррекции АСУ преобразованиями.
Здесь -импульсная функция непрерывной части импульсного фильтра.
Передаточная функция импульсного фильтра определяется как
Wk(z) = Z{ }.
По передаточной функции из таблиц выбирают импульсные корректирующие цепи.
Слайд 81Наиболее просто импульсные КУ реализуются в виде импульсных RC-цепей.
Различают
три структуры импульсных RC-цепей:
последовательную,
с обратной связью и
с
каскадным соединением импульсных цепей первых двух структур.
Цифровые корректирующие фильтры реализуются с помощью цифрового вычислителя. Входной сигнал фильтра x(t) преобразуется в АЦП, далее - решение разностного уравнения на цифровом вычислителе u выводится x[n] в непрерывную часть импульсной АСУ через ЦАП.
Широкое распространение получили цифровые системы, в которых функцию вычислительного устройства выполняют микропроцессоры и компьютеры.
Слайд 82Синтез цифровых систем
сводится к включению цифрового коррек-тирующего фильтра последовательно с
непрерывной частью, включающей в себя объект управления, регулирующий орган, исполнительный
механизм, усилитель мощ-ности и датчик. В качестве желаемых характе-ристик используют аналоговые эквиваленты: импульсные функции, переходные функции и частотные характеристики, что обосновано при достаточно высокой тактовой частоте работы цифрового вычислителя и большой разрядности преобразователей.
![РФ представляет собой числовую последовательность: x[0], x[1T], x[2T], x[3T], ... ,x[nT], ... .Если период дискретности T задан,](/img/thumbs/b8d559f30ab92b34656b80a59b7091ff-800x.jpg "Дискретные системы РФ представляет собой числовую последовательность: x[0], x[1T], x[2T], x[3T], ... ,x[nT],")
![Разности произвольного порядка k определяются по рекуррентным соотношениям: Δk x[n] = Δ{Δk-1 x[n]} = Δk-1](/img/thumbs/6207e42ae00d111e8e92d0e4f6b1412f-800x.jpg "Дискретные системы Разности произвольного порядка k определяются по рекуррентным соотношениям: Δk x[n]")
![Непрерывные АСУ Дискретные АСУ x(t) x[nT] или](/img/thumbs/4672781aaa2f2a5684b41d7adc66730a-800x.jpg "Дискретные системы Непрерывные АСУ Дискретные АСУ x(t) x[nT] или x[n]")
![РУ при использовании (*) можно записать через значения решетчатой функции: При х[n] = 0 это уравнение становится](/img/thumbs/996da3979676f98fbcd7ea50419e6252-800x.jpg "Дискретные системы РУ при использовании (*) можно записать через значения решетчатой функции: При")
![Z -преобразование Z-преобразованием РФ - x[nT] называется функция комплексного аргумента z - X(z) , определяемая](/img/thumbs/c58eacad54b7bd437dc018ffd4c01615-800x.jpg "Дискретные системы Z -преобразование Z-преобразованием РФ - x[nT] называется функция комплексного")
![Структурные схемы и передаточные функции замкнутых дискретных АСУ ПНЧИзображение РФ - y[n] Y(z) = W(z)](/img/thumbs/11020d56e5266b0e72cb2f8383410809-800x.jpg "Дискретные системы Структурные схемы и передаточные функции замкнутых дискретных АСУ ПНЧИзображение")
![Устойчивость импульсных АСУ Линейная импульсная АСУ устойчива, если свободная составляющая переходного процесса yп[n] затухает с](/img/thumbs/547c8e3fd8dd12b0e290cf9a5759ebdb-800x.jpg "Дискретные системы Устойчивость импульсных АСУ Линейная импульсная АСУ устойчива, если свободная")
