Слайд 1Лекция 9. Модели атмосферного рассеяния
Рассмотрим краткое описание моделей атмосферного рассеяния,
рекомендованных в Руководстве АОСС по моделям качества воздуха, акцентируя внимание
на их использовании.
Все эти модели являются гауссовыми моделями рассеяния и отличаются в основном своими приложениями, а не основными принципами построения или расчета. АООС выпускает пакеты прикладных программ, которые делают эти модели сравнимыми с любыми другими, так что, если используются одни и те же условия (например, единственная труба) ответы будут идентичными. Полные описания моделей включены в приложение к Руководству АООС по моделированию.
КМД – климатологическая дисперсионная модель
КМД – это климатологическая гауссова модель непрерывной струи для долгопериодных (сезонных или годовых) среднеарифметических концентраций загрязнения в некоторой точке на уровне земли в городской местности.
Ее более расширенный вариант включает статистическую модель преобразования данных о средних концентрациях в ограниченном числе точек в ожидаемые среднегеометрические и максимальные значения концентраций для нескольких различных времен осреднения.

Слайд 2Гауссова модель качества воздуха для множественных источников
Необходимыми для расчета данными
являются средние объемные скорости выброса (мощности) источника и высота выброса
для точечных или площадных источников, а также температура выбрасываемого газа, скорость истечения его из трубы и внутренний диаметр трубы.
Из метеорологических данных необходимо знать среднюю многолетнюю розу ветров, среднюю высоту послеполуденного слоя перемешивания, среднюю высоту утреннего слоя перемешивания и среднюю температуру воздуха за рассматриваемый период.
В случае, когда производится оценка средних концентраций за короткий период времени, требуется также измеренное стандартное геометрическое отклонение концентраций в исследуемых точках.
На выходе модели получают среднеарифметические концентрации за период от 1 месяца до 1 года или в случае кратковременного периода средние концентрации за период от 1 до 24 ч.
Замечание: Гауссова модель струи используется при определении концентраций пассивной примеси для времени усреднения от часа до суток при выбросе из точечного и площадного источника. Предполагается ровная или слабопересеченная поверхностность. Концентрации рассчитываются для каждого часа. Возможно применение этой модели и для сельской и для городской местности; однако вариант сельской местности не рекомендован для приложения с целью контролирования выбросов.

Слайд 3Входные данные включают данные о выбросе, такие как расположение источника
выброса, мощность выброса, геометрическая высота трубы, скорость выхода газа из
трубы, внутренний диаметр трубы и температура газа.
Метеорологические данные включают ежечасные наземные данные наблюдений за погодой, в том числе высоту слоя облачности и ее мощность, направление и скорость ветра, температуру воздуха, а также высоту слоя дневного перемешивания.
На выходе модели получаются концентрации в каждой исследуемой точке с усреднением от 1 до 24 ч. Составляются перечень вкладов отдельных источников и частотные распределения суммарных концентраций, основанные на 24-ч усреднении. Могут быть получены средние значения концентраций за период более одного года для ограниченного числа точек.
КМПИ – комплексная модель для промышленных источников
КМПИ-модель – это также гауссова модель непрерывной струи, которая может быть использована для оценки концентраций от широкого класса источников, реализующихся в некотором промышленном комплексе.
Эта модель учитывает оседание и сухое выделение частиц, вымывание, а также такие виды источников, как площадной, линейный и объемный. Подъем струи рассматривается как функция расстояния по направлению ветра и вида источника. Предполагаются определенные ограничения в отношении вида подстилающей поверхности. КМПИ-модель работает и при долгопериодном, и при короткопериодном усреднении.

Слайд 4КМПИ – комплексная модель для промышленных источников
В качестве входных данных
используются расположение источника, мощность выброса, постоянная полувыведения загрязнения, высота трубы
(приподнятость источника), скорость выхода примеси из трубы, внутренний диаметр трубы, температура газов, выходящих из трубы, распределение частиц по размерам с соответствующими скоростями оседания, коэффициент отражения примеси поверхностью и размеры соседних зданий.
Метеорологические данные:
За короткий период включают данные ежечасных погодных наблюдений за высотой и плотностью облачного покрытия, скоростью и направлением ветра, температурой, высотой слоя дневного перемешивания.
Длительный период включает сведения о розе ветров, о послеполуденной высоте слоя перемешивания, средней температуре воздуха.
На выходе получают концентрацию и осаждение для определенных времен осреднения, притом более чем для 50 точек. Определяются вторые наивысшие значения концентрации.
Слайд 5МТР – алгоритм гауссовой дисперсии для множественных точечных источников с
учетом особенностей рельефа.
Эта модель полезна при определении концентраций в воздухе
относительно пассивной примеси. Выполняются ежечасные оценки по гауссовой модели непрерывного действия.
Модель может быть использована и для неровной территории, однако местность не должна иметь высоту, большую, чем геометрическая высота трубы.
Внимание! Эта модификация модели действительна только для точечных источников и ее следует применять только для сельской местности.
Входными данными являются мощность выброса, геометрическая высота трубы, скорость выхода из трубы, внутренний диаметр трубы и температура газа в трубе.
В качестве входных метеорологических данных используются данные наземных наблюдений за погодой: высота и плотность облачного покрытия, направление и скорость ветра, температура воздуха высота слоя перемешивания.
В качестве выходных данных получаются усредненные за час и более (до 24ч) концентрации в каждой исследуемой точке и наивысшие из пяти наиболее высоких концентраций в каждой точке за данный период времени.
Модель дает два наивысших значения концентраций за год. Печатается таблица вкладов ограниченного источника.

Слайд 6Модель для единственного источника МЕИ
МЕИ - это гауссова модель стационарной
струи, пригодная как для сельской, так и для городской местности
и для неровной подстилающей поверхности.
Назначение этой модели следующие:
Определить максимальные концентрации для времен усреднения от 1 до 24 ч. в течение года для единичного точечного источника имеющего до 19 труб;
Определить метеорологические условия, при которых наблюдаются максимальные концентрации;
Накопить информацию о концентрациях, необходимую при расчете частотных распределений для различных времен усреднения.
Рассчитывается концентрация для каждого часа года, определяются средние (от ночи до ночи) суточные величины для каждого 24-ч периода. Модель имеет подпрограмму (шаблоны) производящую скользящее усреднение концентраций за 3-, 8-, и 24-ч периоды усреднения.
Входными данными являются мощность источника, геометрическая высота трубы, скорость выхода газов из труб, внутренний диаметр труб и температура газа в трубах.
Входные метеорологические данные – это ежечасные наземные наблюдения за погодой, такие как высота и плотность облаков, направление и скорость ветра, температура воздуха, высота слоя перемешивания.

Слайд 7На выходе модели получают два наивысших значения концентрации в течение
года в каждой исследуемой точке для времен усреднения 1-, 3-
и 24-ч и дополнительно по заданию пользователя для времен усреднения 2 -, 4-, 6-, 8- и 12-ч.
Замечание: Модель дает годовые среднеарифметические величины концентраций для каждой точки, а также для каждых суток наивысшее 1- и 24-ч концентрации по полю исследуемых точек. Ежечасные концентрации для каждой исследуемой точки записываются в память.
Внимание! Это основная (базовая) модель АООС, используемая для рассмотрения единичных источников, в особенности новых электростанций.
При этом предполагается, что все точечные источники находятся в одном месте. Может рассматриваться до 19 источников, собранных в середине сетки полярных координат. Сетка образуется секторами по 10 градусов и пятью расстояниями по радиусу. Учитывается высота местности, причем она должна быть ниже, чем высота труб.
Вывод: Обе модели (МТР и МЕИ) рассматривают концентрацию для неровной местности, уменьшая высоту струи над поверхностью земли, на величину, равную возвышению исследуемой точки над основанием трубы. Машинные программы не позволяют производить вычисления, если местность расположена выше вершины трубы.
Замечание: Для высоких рельефов расчет концентраций производится на так называемой Долинной модели.
Модель для единственного источника МЕИ

Слайд 8Долинная модель
Для рассмотрения случая наихудшего рассеяния в местности со сложным
рельефом разработана специальная целевая модель, которая называется Долинной моделью и
является также разновидностью гауссовой модели.
Горизонтальное распределение направлении, перпендикулярном направлению ветра, принимается равномерным, а не нормальным. Ширина сектора равномерно распределенной концентрации принимается равной 22о5'. Предполагается также, что в устойчивых условиях осевая линия струи огибает неровности рельефа в пределах 10 м от препятствия на соответствующей высоте.
Замечание: Эта модель целиком эмпирическая, она противоречит некоторым физическим принципам, однако она используется в процессе контролирования источника.
Входными данными являются мощность источника, диаметр трубы, высота трубы, температура газа в трубе и скорость истечения газа.
Из метеорологических данных используется многолетняя реальная роза ветров для расчета среднегодовых концентраций или гипотетическая роза ветров для расчета максимальных суточных концентраций.
Выходными данными программы являются расчетные значения концентраций в 112 точках на сетке, образованной 16 азимутальными радиусами и семью различными расстояниями по каждому радиусу.

Слайд 9Другие гауссовы модели
Разработан еще целый ряд других гауссовых моделей. Большая
часть программ для этих моделей рассматривается как способ лучшего и
более эффективного решения для особого класса проблем.
Если они используют кривые рассеяния Паксвилла-Гиффорда, обычный алгоритм для ограничения перемешивания и способ определения подъема струи по Бригсу, то решение для некоторого заданного набора условий должно быть тем же самым, как при использовании моделей АООС, рассмотренных выше.
Некоторые модели вводят изменения боковой (поперечной) дисперсии в зависимости от времени или используют различные методы определения подъема струи и высоты слоя перемешивания.
Замечание: По мнению специалистов большинство этих моделей не являются более точными, чем модели АООС, а в некоторых случаях даже менее точны.
Гораздо более важен метод определения коэффициентов дисперсии (СКО) σY и σZ, чем незначительные расхождения, имеющиеся между большей частью гауссовых моделей.
Слайд 10Численные модели
Этот класс моделей является более сложным, чем гауссовы модели.
Соответственно и программы тоже более сложны.
Все модели основываются на
численных решениях уравнений К-теории.
При эйлеровой формулировке задачи рассматривается эйлерова фиксированная система координат или сетка, которая покрывает весь исследуемый район. Концентрация в каждом квадрате или ячейке сетки рассматривается путем решения исходного уравнения численными методами.
Внимание! Этот подход наиболее полезен для ситуаций, в которых имеются множественные источники, и есть необходимость прогнозировать концентрации.
При лагранжевой формулировке задачи система координат движется вместе с переносящим ветром.
Внимание! Этот подход полезен для единичных источников, в том числе единичных площадных источников, или для моделирования переноса примеси на большие расстояния. В таком случае не получаются концентрации на обширной сетке, как при эйлеровой задаче.
Слайд 11Вывод: Метод Лагранжа экономит машинное время, но дает результаты, которые
трудно бывает интерпретировать, т.к. система координат искривляется.
Внимание! Определенная группа
лагранжевых моделей, называемых траекторными моделями, избегает искривления координат при переносе единичной движущейся ячейки, но имеет другие проблемы за счет пренебрежения некоторыми деталями и упрощения процесса диффузии.
Замечание: Одним из способов решения, который встречается в смешанных методиках, называется "частица в ячейке". При этом выбросы источников делятся по разным лагранжевым ячейкам, каждая из которых движется в фиксированной системе координат. Концентрация в каждом фиксированном квадрате сетки рассчитывается путем подсчета числа ячеек в каждом квадрате.
Все наиболее популярные численные модели хорошо описаны в учебниках.
В качестве примера эйлеровой модели можно привести модель LIRAQ и модель Airshed, используемую АООС в некоторых приложениях.
Примером лагранжевой модели является применяемая АООС модель реагирующей струи. Пример модели "частица в ячейке" - модель ADPIS.
Численные модели

Слайд 12Большая часть существующих данных пригодна для использования при моделировании. Определенные
концентрации прямо пропорциональны мощности выброса и направлению ветра, однако чувствительность
концентраций по отношению к другим параметрам не всегда однозначна.
Внимание! Наборы данных и соответствующие процедуры определения входных параметров представляют собой существенную часть процесса моделирования. Некоторые из переменных, необходимых для ввода в модель, должны быть измерены непосредственно или постоянно иметься в наличии.
В моделях АООС используются процессы, преобразующие имеющиеся данные об источниках и метеорологические данные в форму, применяющуюся в моделях прогноза качества воздуха.
Вывод: Для оценки вклада источника важно учитывать различные условия выброса и достаточно широкий диапазон метеорологических условий, базирующийся на данных многолетних наблюдений. Может быть достаточна даже первичная информация в тех случаях, когда максимальная концентрация выбрасываемой источником примеси существенно ниже предельно допустимых величин.
Лекция 10. Условия однозначности моделей
Данные, используемые в моделях

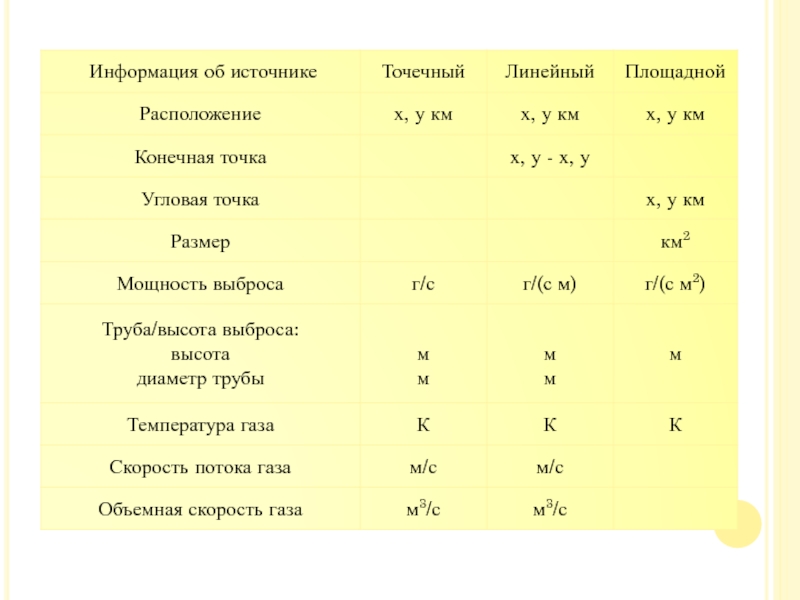
Слайд 13Источники можно классифицировать по трем основным категориям: точечные, линейные и
площадные.
Точечные источники – это отдельные трубы.
Линейные источники –
это чаще всего автомагистрали (дороги), но также и длинные здания.
Площадным источником может являться группа зданий, автомагистраль и хранилища, которые превышают нормы выброса.
Внимание! Обычно для площадных источников все выбросы суммируются и создают некоторую среднюю величину выброса по всей рассматриваемой площади.
Необходимые переменные, используемые в моделях АООС, представлены в таблице.
Замечание: При прогнозе наибольшего загрязнения обычно используется полная проектная мощность выброса. Некоторые приподнятые источники могут в особых обстоятельствах создавать более приземные концентрации при нагрузке, меньшей 100%. Это может быть проверено для больших точечных источников, если делать расчеты для 50- и 75%-ной нагрузки.
Данные об источнике
Слайд 15Внимание! Метеорологические данные, используемые в любом процессе моделирования, должны представительно
описывать условия переноса и рассеяния в рассматриваемом регионе.
Замечание: Представительность
данных зависит от близости станции метеорологической сети к рассматриваемой территории, укомплектованности станции, состояния метеорологического оборудования для измерений, периода времени, в течение которого набирались метеорологические данные.
На представительность могут влиять расстояние, разность скоростей и направления ветра на высоте измерения переноса и особенности рельефа, такие как холмы и большие водоемы.
Вывод: Метеорологическими данными, необходимыми для описания переноса и рассеяния, в большинстве моделей являются скорость и направление ветра, устойчивость атмосферы, температура и высота слоя перемешивания. Желательны и более подробные данные, но они редко имеются в наличии.
Метеорологические данные
Слайд 16Внимание! Для обобщенных данных необходимы сведения о преобладающих направлениях ветра,
средних скоростях ветра, температуре воздуха и общей облачности. Если концентрации
загрязнения оказываются малыми по сравнению с нормами или приростом, то необходимость более детального анализа отпадает.
Замечание: Если источник мощный, то АООС требует анализа, основанного на использовании не менее чем пятилетнего ряда данных. Для расчета среднегодовых концентраций используется повторяемость направлений и скоростей ветра и средняя высота слоя перемешивания. Такой модельный расчет для пятилетнего периода требует не более времени, чем для периода один год.
Справочно: Однако краткопериодные стандарты (нормы) и усреднения за 1, 3, 8, 24 ч требуют расчетов на существующих моделях для каждого часа за период 5 лет.
Метеорологические данные
Качество воздуха
Некоторые модели включают использование данных о существующем качестве воздуха либо учета фонового загрязнения, к которому добавляются моделируемое локальное загрязнение и формируется полная концентрация, либо как средство "калибровки" сезонных или годовой модели.

Слайд 17Сравнение прогнозируемых среднегодовых концентраций с наблюдаемыми годовыми концентрациями, проведенное Пасквилом
показало, что модели согласуются с наблюдениями в пределах 20...30% отклонений.
Среднегодовое усреднение дает более сглаженное изменение концентраций, чем короткие периоды усреднения, и не так чувствительно к особенностям локальных изменений направления ветра и условий устойчивости.
Вывод: При уменьшении периода усреднения ухудшается соответствие между расчетом по моделям и наблюдаемыми концентрациями. Проверка моделей АООС в процессе прогнозирования усредненных концентраций за один час для низких источников и ненагретых приподнятых источников показала, что в 65% случаев расчетные концентрации примеси от источников, расположенных вблизи земли, примерно в два раза отличались от наблюдаемых концентраций.
Точность моделей
Низкие источники
Для проверки точности нескольких моделей Лондержан воспользовался данными экспериментов с трассерами, которые первоначально использовались для разработки кривых устойчивости атмосферы. Он сравнил наблюдаемое и прогнозируемое расположение осевой линии струи, ширину струи, интегральные концентрации по сечению струи и максимальные концентрации.

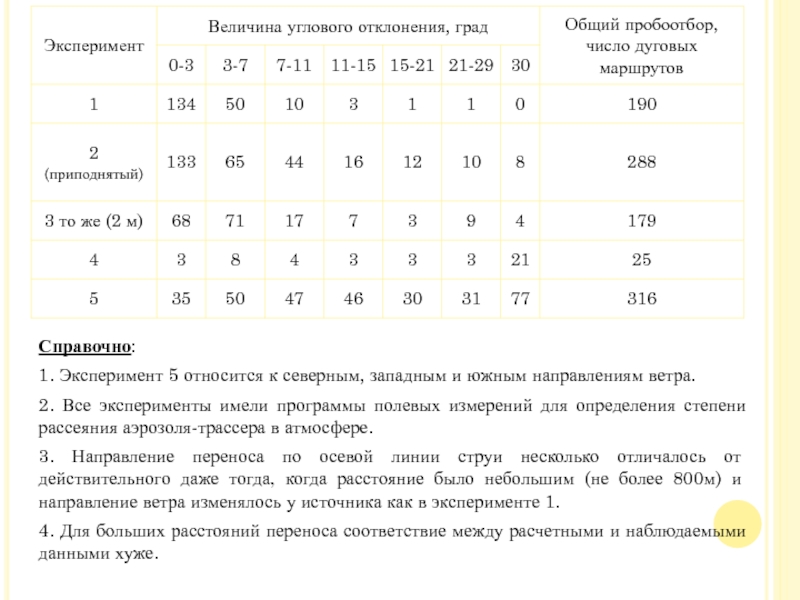
Слайд 18Справочно:
1. Эксперимент 5 относится к северным, западным и южным
направлениям ветра.
2. Все эксперименты имели программы полевых измерений для определения
степени рассеяния аэрозоля-трассера в атмосфере.
3. Направление переноса по осевой линии струи несколько отличалось от действительного даже тогда, когда расстояние было небольшим (не более 800м) и направление ветра изменялось у источника как в эксперименте 1.
4. Для больших расстояний переноса соответствие между расчетными и наблюдаемыми данными хуже.
Слайд 19Низкие источники
В эксперименте 5 в точке выброса не было анемометров
и примерно в 73% случаев расчетные положения осевой линии струи
отличались от наблюдаемых более чем на 7 град. Ошибка в 7 град в положении струи при категории устойчивости С приводит к ошибке в 2 раза в величине концентрации на расстоянии 2-х километров.
Ширина струй, определенная в соответствии с системой классификации устойчивости АООС с учетом облачного покрытия и скорости ветра, близка к наблюдаемой ширине струй. Различие увеличивается для устойчивых условий. Средняя предсказанная ширина струи составляла примерно 75% от наблюдений. Для экспериментов с приподнятым источником в неустойчивых условиях прогнозируемая ширина струи оказалась равна наблюдаемой. Среднее отношение прогнозируемой ширины к наблюдаемой равно единице.
Сравнение интегральных по сечению струи концентраций позволяет проверить коэффициент вертикальной дисперсии (СКО).
Вывод: Лондержан пришел к заключению, что данные эксперимента №1 дают хорошее согласие между прогнозируемыми и наблюдаемыми величинами интегральных по сечению струи концентраций.

Слайд 20Низкие источники
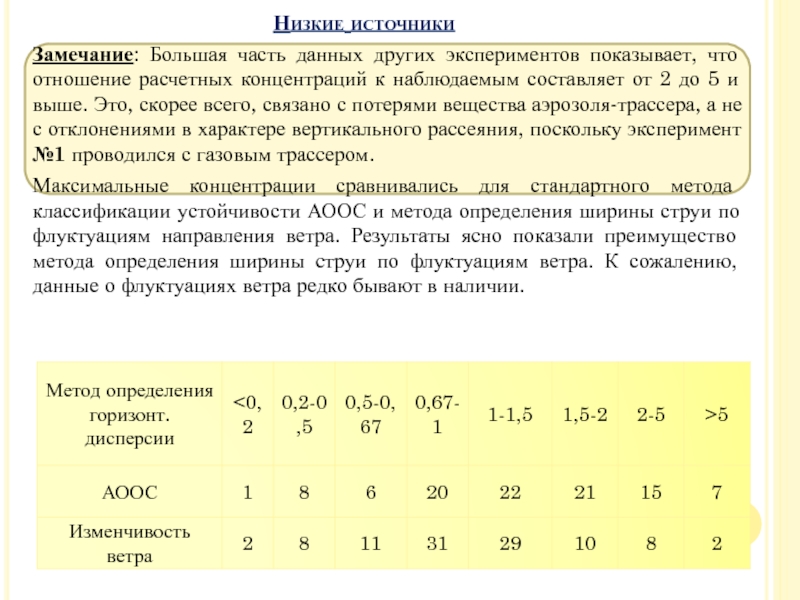
Замечание: Большая часть данных других экспериментов показывает, что отношение
расчетных концентраций к наблюдаемым составляет от 2 до 5 и
выше. Это, скорее всего, связано с потерями вещества аэрозоля-трассера, а не с отклонениями в характере вертикального рассеяния, поскольку эксперимент №1 проводился с газовым трассером.
Максимальные концентрации сравнивались для стандартного метода классификации устойчивости АООС и метода определения ширины струи по флуктуациям направления ветра. Результаты ясно показали преимущество метода определения ширины струи по флуктуациям ветра. К сожалению, данные о флуктуациях ветра редко бывают в наличии.
Слайд 21Приподнятые источники нагретых выбросов
Выбросы из высоких труб исследовались путем сравнения
наблюдаемых приземных концентраций диоксида серы и газового трассера с концентрациями,
рассчитанными по модели АООС. Эксперименты проводились на очень ровной местности.
Сравнение расчетов по модели МТР АООС с наблюдаемыми концентрациями показывает, что модельные расчеты усредненных за 1 час максимальных концентраций, ожидаемых в течение сезона или года, вполне удовлетворительны. Однако изолинии наблюдаемых приземных концентраций образуют область на 60% шире, чем для прогнозируемых по модели концентраций.
Внимание! Другие аналогичные модели прогнозируют более широкую область по величинам приземной концентрации и вследствие этого меньшие, чем наблюдаемые, величины максимальных концентраций.
Вывод: Эти результаты доказывают допустимость использования модели для приподнятых нагретых источников при оценке максимальных (осевых) концентраций, которые могут наблюдаться в течение некоторого периода времени, такого как месяц и год, но эта модель не может использоваться для расчета концентрации в фиксированной точке в определенное время.

Слайд 22Лекция 11. Примеры расчета по моделям АООС
Простые источники
Пример №1 Пусть
происходит непрерывный выброс газа из поврежденного резервуара в открытой и
ровной местности. Мощность выброса Q = 100 г/с. Требуется определить максимальную (осевую) концентрацию на расстоянии 500 м от источника.
Метеорологические условия: температура – 15оС, скорость ветра 3 м/с, стандартное отклонение направления ветра 18 град.
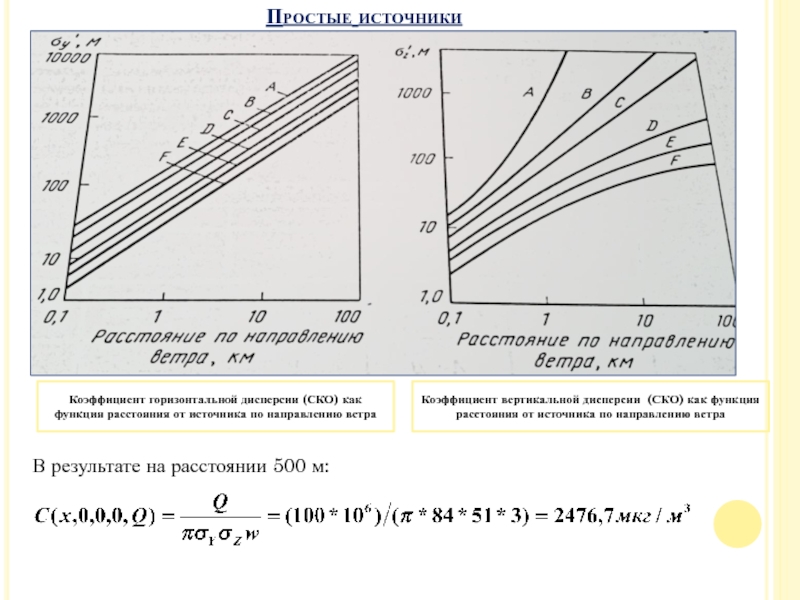
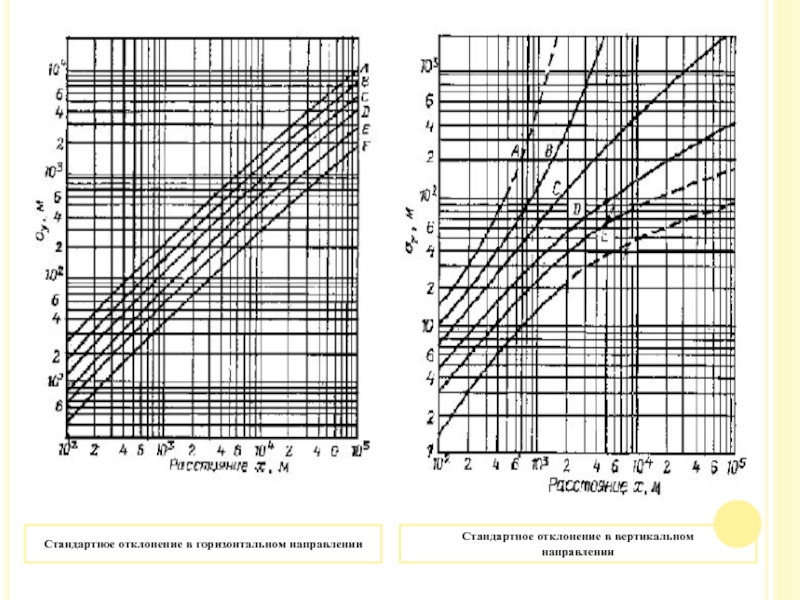
По таблице 2 определяем класс устойчивости В. Значение σY на 500 м и направление ветра в соответствии с рис. 1 – 84м. Значение на расстоянии 500 м от источника в соответствии с рис. 2 – 51м. АООС обычно в качестве единиц измерения концентрации использует мкг/м3.
Слайд 23Простые источники
В результате на расстоянии 500 м:
Коэффициент горизонтальной дисперсии (СКО)
как функция расстояния от источника по направлению ветра
Коэффициент вертикальной дисперсии
(СКО) как функция расстояния от источника по направлению ветра
Слайд 24Стандартное отклонение в горизонтальном направлении
Стандартное отклонение в вертикальном
направлении
Слайд 25Простые источники
Пример №2 Пусть газ выбрасывается из трубы высотой 25
м, со следующими параметрами: диаметр –1м, температура газа 330 К,
скорость выхода газа 10 м/с, расстояние до исследуемой точки 500 м.
Метеорологические условия: температура – 15оС, скорость ветра 3 м/с, стандартное отклонение направления ветра 18 град.
Определяем подъем струи используя:
расстояние до исследуемой точки 500м > 3,5X*=99,4м, и
Слайд 26Простые источники
Для такого источника осевая концентрация задается уравнением:
в котором величина Н = 25+16,7=41,7м.
Пример 3: Определить концентрацию на расстоянии 150 м перпендикулярно к осевой линии струи на удалении 500 м от источника по направлению ветра при аналогичных параметрах.
Слайд 27Простые источники
Примеры 1...3 показывают все шаги по определению концентраций от
простого источника с учетом влияния на величину приземной концентрации эффекта
выбрасывания через трубу (пример 2) и удаления от центра струи по направлению к ее краю (пример 3).
Проблема влияния аэродинамической тени зданий на расстояние выбросов из труб и вентиляционных отверстий на крышах зданий часто встречается на практике.
Пример 4: Условия и параметры, необходимые для выполнения соответствующих расчетов, представлены ниже:
Слайд 28Простые источники
а) Рассчитываем эффективную высоту струи (с учетом подъема)
б)
Сравниваем высоту струи Н с высотой здания hb;
если H≤1,2hb,
принимаются модифицированные значения σY и σZ;
если 1,2hb если H>2,5hb значения σY и σZ не модифицируются, а источник рассматривается как труба за пределами тени здания.
в) Определяются соответствующие уравнения и рассчитываются величины σ’Y и σ’Z
г) Рассчитываются соответствующие концентрации.
В соответствии с этими шагами производятся расчеты.
Расстояние до исследуемой точки ρ=200 >3,5*5=17,5м
Слайд 29Простые источники
Н=32+1,57= 33,57 м; Н
x = 200 м принимаются модифицированные значения σY и σZ.
Концентрацию
находим из выражения:
Если действует множество источников или нужны горизонтальные профили концентрации, расчеты становятся сложнее и обычно используются машинные программы.
Расчеты усложняются также и за счет других факторов, таких, например, как ограничение рассеяния инверсионным слоем, которые требуют решения написанных выше уравнений с тройным суммированием четырех экспоненциальных членов. Аналогичные трудности встречаются и при учете осаждения и вымывания.
Слайд 30Лекция 12. Методика расчета концентраций в атмосферном воздухе загрязняющих веществ,
содержащихся в выбросах предприятий
Основным документом, регламентирующим рассеивание и определение приземных
концентраций примесей из источников выбросов в России, является «Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий ОНД-86».
Методика разработана на базе ряда упрощений и усреднений. В ней отдельные факторы объединены в усредненные группы и численно учитываются комплексными обобщенными коэффициентами.
Методика предназначена для решения практических задач, связанных с прогнозом загрязнения атмосферного воздуха, и использует формулы, полученные на основе решения уравнения турбулентной диффузии.
Методика позволяет производить расчеты рассеивания примесей, выбрасываемых в атмосферу одиночными точечными, линейными источниками и группой источников, с учетом влияния рельефа местности, определять предельные концентрации загрязняющих веществ в двухметровом слое над поверхностью земли, а также вертикальное распределение концентраций.
Слайд 31Методика расчета концентраций в атмосферном воздухе загрязняющих веществ
Степень загрязнения атмосферного
воздуха определяется наибольшим расчетным значением концентрации, соответствующим неблагоприятным метеорологическим условиям,
опасной скорости ветра.
Для веществ, обладающих суммацией вредного действия, безразмерная суммарная концентрация q (в долях ПДК) и суммарная концентрация С, приведенная к веществу C1, рассчитывается с использованием для каждого источника значений мощности Мq и М соответственно:
где С1, ПДК1 – концентрация и ПДК вещества, к которому осуществляется приведение;
С2,…Сn и ПДК2,…ПДКn – концентрации и ПДК других веществ, входящих в рассматриваемую группу.
Слайд 32Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Максимальное значение
приземной концентрации загрязняющего вещества См, (мг/м3) при выбросе газовоздушной смеси
из одиночного точечного источника с круглым устьем достигается при неблагоприятных метеорологических условиях на расстоянии Хм и определяется по формуле:
(**)
Первую формулу применяют для холодных выбросов, т.е. при ΔТ ≈ 0
где А — коэффициент, зависящий от температурной стратификации атмосферы (140÷250 для стран СНГ);
М — масса загрязняющего вещества, выбрасываемого в атмосферу в единицу времени, г/с;
F — коэффициент, учитывающий скорость оседания загрязняющих веществ в воздухе; т,
m, n — коэффициенты, учитывающие условия выхода газовоздушной смеси из устья источника выброса;
Слайд 33Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Н —
высота источника выброса над уровнем земли, м; (для наземных источников
принимается Н = 2 м);
η — коэффициент, учитывающий влияние рельефа местности (в случае ровной или слабопересеченной местности с перепадом высот не более 50м/км принимается η = 1);
V1 — объемный расход газовоздушной смеси, м3/c;
ΔT - разность между температурой выбрасываемой газовоздушной смеси и температурой окружающего воздуха, oC.
Вывод: Максимальная концентрация загрязняющего вещества в приземном слое атмосферы прямо пропорциональна массовому расходу загрязняющего вещества М и обратно пропорциональна квадрату высоты источника - Н2.
Коэффициент А при неблагоприятных метеорологических условиях, обеспечивающих максимальные значения концентраций загрязняющих веществ в приземном слое атмосферы, имеет следующие значения:
для источников севернее 52о с.ш. А = 160;
для источников в зоне от 50 до 52о с.ш. А = 180;
для источников южнее 50о с.ш. — А = 200.
Слайд 34При определении ΔТ температуру окружающего атмосферного воздуха принимают равной средней
температуре наружного воздуха наиболее жаркого месяца года в 1300 по
местному времени.
Значения коэффициента F:
• для газообразных загрязняющих веществ и мелкодисперсных аэрозолей, скорость оседания которых близка к нулю, F = 1;
• для прочих мелкодисперсных аэрозолей при степени очистки газов в пылеуловителе η ≥ 0,9 F = 2; при 0,75≤ η < 0,9 F = 2,5; при η < 0,75 F = 3;
• при наличии данных о дисперсном составе пыли в зависимости от соотношения Vg/Um при Vg/Um ≤ 0,015 F = 1; при 0,015
где: Vg — скорость витания частиц такого диаметра dg, что масса всех частиц диаметром больше dg составляет 5% от общей массы частиц, м/с; Um — опасная скорость ветра, м/с.
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Слайд 35Для получения значений коэффициентов m и n определяются следующие промежуточные
коэффициенты:
(****)
где: D — диаметр устья дымовой трубы, м; wo — скорость выхода газовоздушной смеси из дымовой трубы, м/с.
Коэффициент m определяется по формуле:
При f e < f < 100 при расчете m принимают f =fe.
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
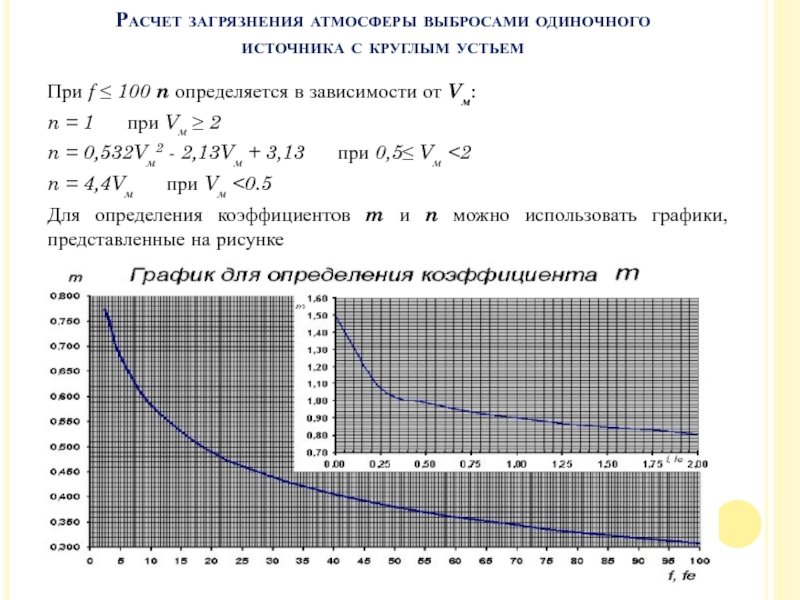
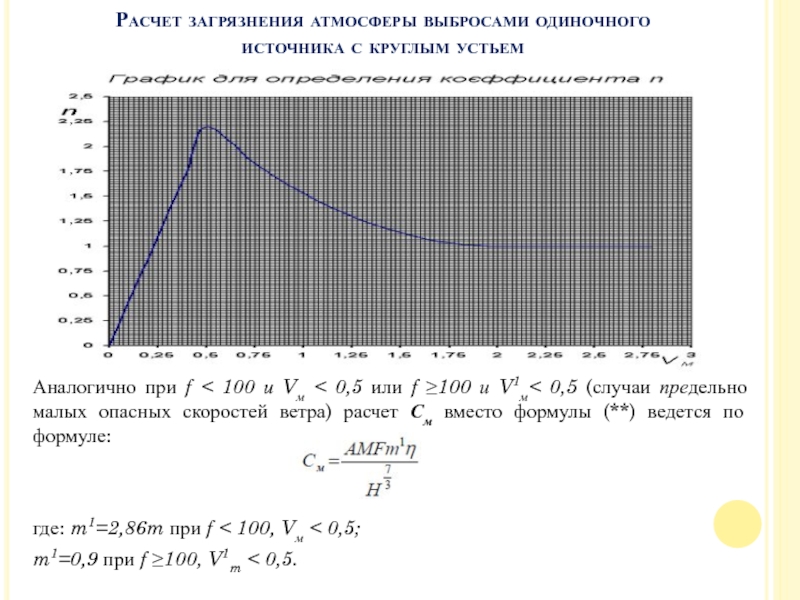
Слайд 36При f ≤ 100 n определяется в зависимости от Vм:
n
= 1 при Vм ≥ 2
n = 0,532Vм2
- 2,13Vм + 3,13 при 0,5≤ Vм <2
n = 4,4Vм при Vм <0.5
Для определения коэффициентов m и n можно использовать графики, представленные на рисунке
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Слайд 37
Аналогично при f < 100 и Vм < 0,5 или
f ≥100 и V1м< 0,5 (случаи предельно малых опасных скоростей
ветра) расчет См вместо формулы (**) ведется по формуле:
где: m1=2,86m при f < 100, Vм < 0,5;
m1=0,9 при f ≥100, V1m < 0,5.
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Слайд 38Расстояние хм, м, на котором приземная концентрация С, мг/м3 при
неблагоприятных метеоусловиях достигает максимального значения См, определяется по формуле:
где d
– безразмерный коэффициент рассчитывают по формулам
При f <100:
При f > 100 или ΔТ≈ 0 значения d находят по формулам:
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Слайд 39Значение опасной скорости ветра U м, при которой достигается наибольшее
значение приземной концентрации загрязняющих веществ С м:
При f < 100:
При
f ≥100 или ΔТ≈0:
При опасной скорости ветра Uм, (м/с) приземная концентрация загрязняющих веществ С, (мг/м3) в атмосфере по оси факела выброса на расстоянии Х от источника определяется по формуле:
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
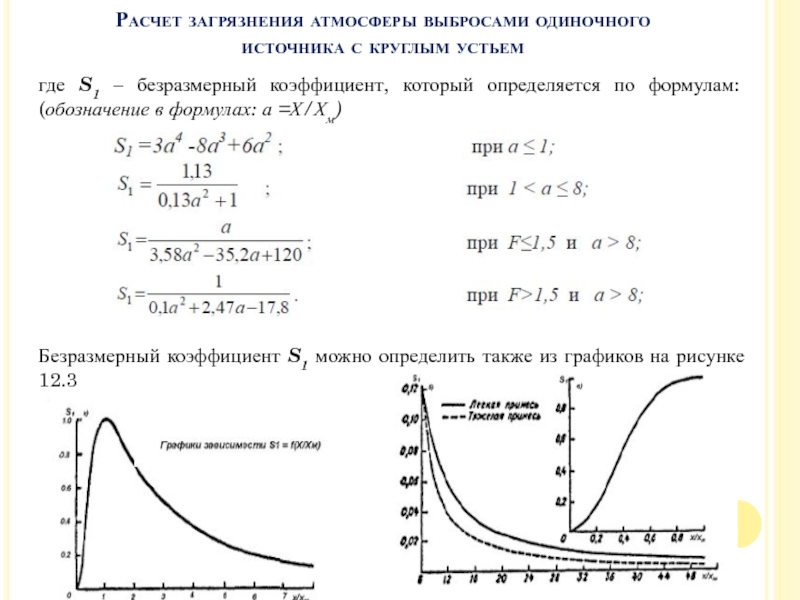
Слайд 40где S1 – безразмерный коэффициент, который определяется по формулам: (обозначение
в формулах: а =Х/Хм)
Безразмерный коэффициент S1 можно определить также из
графиков на рисунке 12.3
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Слайд 41Для низких и наземных источников при 2м≤Н≤10м и Х/Хм
S1 заменяется на S1H = 0,125(10-Н) +0,125(Н-2)S1.
Значения приземной концентрации загрязняющих
веществ в атмосфере Су, мг/м3, на расстоянии у, м по перпендикуляру к оси факела выброса определяют по формуле:
где S2 – безразмерный коэффициент (зависит от скорости ветра U и отношениия у/х) определяют по значению аргумента ty по формуле:
Расчет загрязнения атмосферы выбросами одиночного источника с круглым устьем
Слайд 42Расчеты загрязнения атмосферы при выбросах газовоздушной смеси из источника с
прямоугольным устьем (шахты) проводятся по приведенным выше формулам при средней
скорости ωо и значениях D=Dэ,(м) и V1=V1э (м3/c).
Средняя скорость выхода в атмосферу газовоздушной смеси ωо (м/с) определяется по формуле:
где L(м) — длина устья; b (м) — ширина устья.
Эффективный диаметр устья Dэ (м) определяется по формуле:
Эффективный расход выходящей в атмосферу в единицу времен газовоздушной смеси V1э (м3/c) определяется по формуле:
(***)
Лекция 13. Расчеты загрязнения атмосферы выбросами источника с прямоугольным устьем
Слайд 43Радиус зоны влияния для каждого источника рассчитывается как наибольшее из
двух расстояний Х1 и Х2, где Х1=10Хм, а величина Х2
– определяется как расстояние от источника, начиная с которого С ≤ 0,05 ПДК.
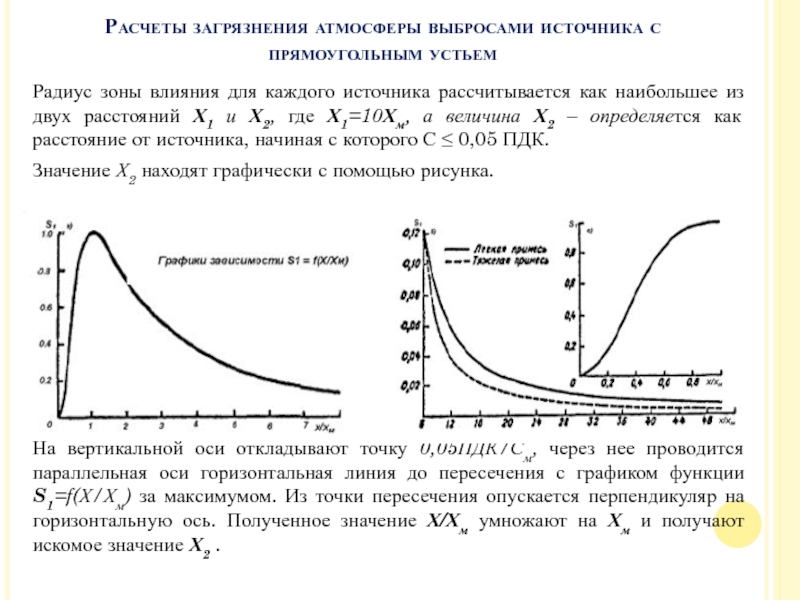
Значение Х2 находят графически с помощью рисунка.
На вертикальной оси откладывают точку 0,05ПДК/См, через нее проводится параллельная оси горизонтальная линия до пересечения с графиком функции S1=f(Х/Хм) за максимумом. Из точки пересечения опускается перпендикуляр на горизонтальную ось. Полученное значение Х/Хм умножают на Хм и получают искомое значение Х2 .
Расчеты загрязнения атмосферы выбросами источника с прямоугольным устьем
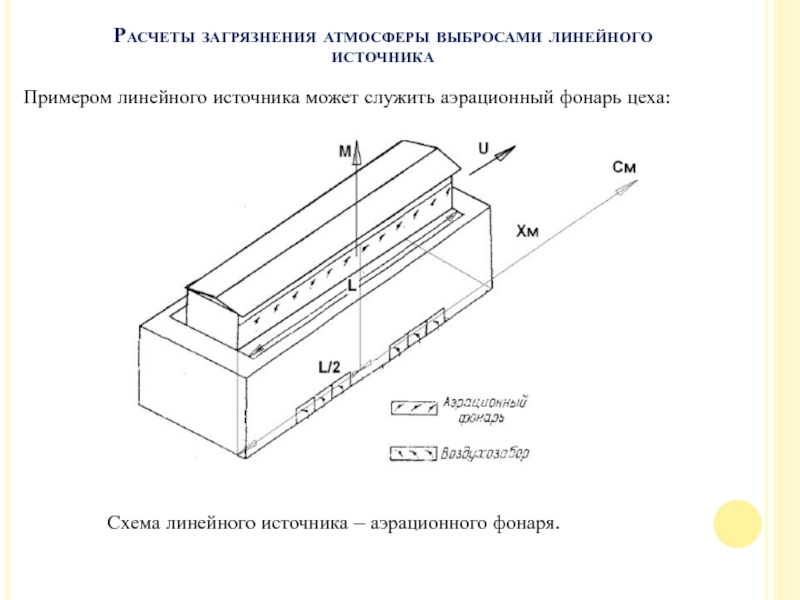
Слайд 44Примером линейного источника может служить аэрационный фонарь цеха:
Расчеты загрязнения атмосферы
выбросами линейного источника
Схема линейного источника – аэрационного фонаря.
Слайд 45При расчете рассеивания выбросов от линейного источника длиной L наибольшая
концентрация вредной примеси См достигается в случае ветра вдоль источника
на расстоянии Хм от проекции его центра на земную поверхность. При рассмотрении аэрационного фонаря как линейного источника значения См (мг/м3) и расстояния Хм (м) определяются по формулам:
3десь значения С1м и Х1м, а также соответствующее им значение U1м принимаются равными максимальной концентрации См, расстоянию Хм и опасной скорости Uм для одиночного источника той же мощности М с круглым устьем диаметром Dэ и расходом выбрасываемой газовоздушной смеси V1э.
Расчеты загрязнения атмосферы выбросами линейного источника
Слайд 46При этом эффективный диаметр устья фонаря Dэ (м) определяется по
формуле:
где V1 - м3/c - расход выбрасываемой из фонаря в
единицу времени газовоздушной смеси, wo (м/с) - средняя скорость выхода из фонаря газовоздушной смеси. Величина V1э определяется по найденному значению Dэ и формуле (***).
За высоту источника вы6роса Н(м) принимается высота над уровнем земли верхней кромки фонаря.
Безразмерные коэффициенты S3 и S4 определяются в зависимости от отношения L/XIм по формулам:
Расчеты загрязнения атмосферы выбросами линейного источника
Слайд 47При произвольном направлении ветра по отношению к линейному источнику типа
аэрационного фонаря этот источник условно представляется в виде группы N
одинаковых равноудаленных точечных источников.
Для каждого из этих одиночных источников значения максимальной концентрации вредной примеси См и соответствующих ей расстояния Хм и опасной скорости Uм определяются как:
Число одинаковых равноудаленных одиночных источников N, на которое делится аэрационный фонарь при расчетах, определяется (с округлением до ближайшего большего целого числа) по формуле:
где х (м) - наименьшее расстояние от аэрационного фонаря до расчетной точки на местности, u - расчетная скорость ветра.
Расчеты загрязнения атмосферы выбросами линейного источника
Слайд 48Приземная концентрация вредных веществ в любой точке местности при наличии
N источников определяется как сумма концентраций веществ от отдельных источников
при заданном направлении и скорости ветра:
С=С1+ С2 +….+СN + Сф
где С1, С2, СN — концентрации вредного вещества соответственно от первого, второго, N-го источников, расположенных с наветренной стороны при рассматриваемом направлении ветра; Сф - фоновое загрязнение.
Слагаемое Сф в правой части уравнения добавляется в случае, когда имеются неучтенные (фоновые) источники выбросов того же вещества или веществ, обладающих с ним эффектом суммации (от других предприятий, других промышленных районов).
В целях ускорения и упрощения расчетов количество рассматриваемых источников выбросов сокращается путем их объединения (особенно мелких источников) в отдельные условные источники. Подобное объединение возможно при соблюдении определенных условий.
Расчеты загрязнения атмосферы выбросами группы источников и площадных источников
Слайд 49Значение максимальной суммарной концентрации от N расположенных на площадке близко
друг от друга одиночных источников, имеющих равные значения высоты, диаметра
устья, скорости выхода в атмосферу и температуры газовоздушной смеси, определяется по формуле:
где М (г/с) – суммарная мощность выброса всеми источниками в атмосферу;
V (м3/с) – суммарный расход выбрасываемой всеми источниками газовоздушной смеси, определяемый по формуле:
V=V1*N
Значение параметра Vм определяется по формуле:
Расчеты загрязнения атмосферы выбросами группы источников и площадных источников
Слайд 50В остальном схема расчета концентраций веществ для выбросов от группы
близко расположенных источников не отличается от расчета выбросов одиночного источника.
В
случае, когда См от группы мелких источников по рассматриваемому веществу не превышает 0,05 ПДК, указанные источники могут быть исключены из рассмотрения.
Для ускорения и упрощения расчетов приземных концентраций на каждом предприятии рассматриваются те из выбрасываемых вредных веществ, для которых:
где М (г/с) – суммарное значение выброса от всех источников предприятия, соответствующее наиболее неблагоприятным из установленных условий выброса, включая вентиляционные источники и неорганизованные выбросы; ПДК (мг/мЗ) - максимальная разовая предельно допустимая концентрация; H (м) – средневзвешенная по предприятию высота источников выброса.
Расчеты загрязнения атмосферы выбросами группы источников и площадных источников
Слайд 51где М(0-10), М(11-20), М(21-30) … - суммарные выбросы вещества в
интервале высот источников до 10 м включительно, 11-20м, 21-30м и
т.д.
Расчеты загрязнения атмосферы выбросами группы источников и площадных источников
Слайд 52Решение обратных задач предполагает определение мощности выброса М и высоты
трубы Н, соответствующих заданному уроню максимальной приземной концентрации См при
прочих фиксированных параметрах выбросов.
Мощность выброса М г/с, соответствующая заданному значению максимальной концентрации См (мг/м3), определяется по формуле:
В случае f≥100 или ΔТ≈0
Значение минимальной высоты при горячих выбросах (ΔТ>0) первоначально определяется из выражения:
Решение обратных задач
Слайд 53Если найденное значение
, то оно является окончательным. В
противном случае предварительное значение минимальной высоты определяется по формуле:
По найденному значению Н определяются величины коэффициентов f, Vм, Viм, fe по формулам (****) и получают в первом приближении коэффициенты m=m1 и n=n1. Если произведение m1 n1 ≠ 1, то по величинам m1 и n1 определяют второе приближение Н=Н2 по формуле:
В общем случае (i+1) приближение Нi+1 определяется по формуле:
где m1 и n1 соответствуют Нi , а mi-1 и ni-1 - Нi-1.
Уточнение значения Н необходимо производить до тех пор, пока найденные значения Нi и Нi-1 практически будут равны друг другу (с точностью до 1 метра).
Решение обратных задач
Слайд 54Влияние рельефа местности на величину максимальной приземной концентрации учитывается безразмерным
коэффициентом η.
Значение η устанавливается на основе анализа картографического материала, в
радиусе до 50 высот наиболее высокого из размещаемых на промплощадке источника, но не менее чем до 2 км.
Если в окрестности рассматриваемого источника выбросов (предприятия) имеются отдельные изолированные препятствия, вытянутые в одном направлении (гряда, гребень, ложбина, уступ), то поправочный коэффициент на рельеф η определяется по формуле:
где ηm – безразмерная величина, зависит от форм рельефа и определяется по таблице в зависимости от величин n1 и n2:
Лекция 14. Учет влияния рельефа местности при расчете
загрязнения атмосферы
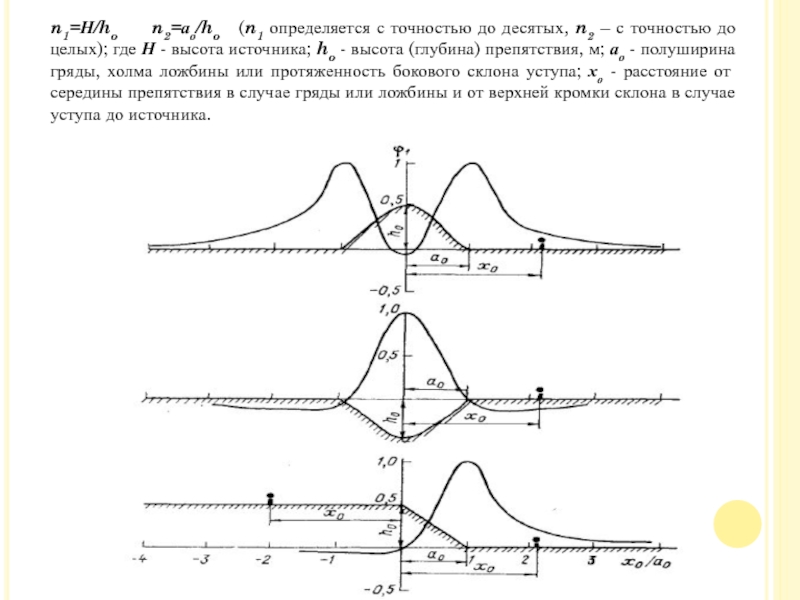
Слайд 55n1=Н/ho n2=ао/ho (n1 определяется с точностью
до десятых, n2 – с точностью до целых); где Н
- высота источника; ho - высота (глубина) препятствия, м; ао - полуширина гряды, холма ложбины или протяженность бокового склона уступа; хо - расстояние от середины препятствия в случае гряды или ложбины и от верхней кромки склона в случае уступа до источника.
Слайд 56Значение функции φ1 определяется в зависимости от отношения lхоl/ао по
графикам, соответствующим различным формам рельефа.
Если препятствие представляет собой отдельный холм
или ложбину (впадину), то ho выбирается соответствующим максимальной (минимальной) отметке препятствия, а n2 - максимальной крутизне склона, обращенного к источнику.
Для источников выброса, расположенных в зоне влияния нескольких изолированных препятствий, определяются значения η для каждого препятствия и в расчете используется максимальное из них.
Учет влияния рельефа местности при определении расстояния Хм, где достигается максимум приземной концентрации, осуществляется путем умножения коэффициента d в формуле
на отношение:
При расчете приземных концентраций по оси факела на различных расстояниях от источника по формуле Сх = S1Cм отношение Х/Хм определяется с учетом последней поправки для значений
при η=1 – условия ровной или слабо пересеченной местности).
Для больших значений Х при вычислении Х/Хм используют значения
Слайд 57Фоновая концентрация - статистически достоверная максимальная концентрация, Сф, мг/м3. Она
является характеристикой загрязнения атмосферы и определяется как значение концентрации, которое
превышается не более чем в 5% случаев от общего количества наблюдений.
Сф характеризует суммарную концентрацию, создаваемую всеми источниками, расположенными на данной территории.
Сф устанавливается для каждого вещества по данным наблюдений. При отсутствии необходимых данных наблюдений фоновая концентрация может быть определена расчетным путем.
Период определения Сф
Обработка данных результатов наблюдений
Определение Сф для каждого поста наблюдений производится по данным за период от 3 до 5 лет (не менее 3-х лет). Выбранный период должен соответствовать следующим условиям:
1. число наблюдений в течение года должно быть не менее 200 по каждому
веществу, а общее число наблюдений за выбранный период - не менее 800;
2. методики отбора и анализа проб должны быть неизменными;
3. расположение поста наблюдений не менялось;
4. характер застройки в районе наблюдательного поста существенно не изменялся;
5. существенных изменений в характеристиках промышленных выбросов в радиусе 5 км от поста не происходило.
Фоновые концентрации загрязняющих веществ
в атмосферном воздухе

Слайд 58Для определения Сф могут быть использованы данные как стационарных, так
и подфакельных постов наблюдений.
В результате обработки данных для каждого поста
по всему массиву результатов наблюдений находят величины Сфi (где: i = 0;1;2;3;4), соответствующие различным градациям направления α и скорости ветра W (таблица).
Верхняя граница скорости ветра W* определяется из условия, что скорость ветра в данном месте W> W* встречается в 5% случаев.
При определении Сфi для каждой из пяти градаций скорости и направления ветра значения концентраций qk (k - номер концентрации в i-ой градации) вписываются в таблицу, после чего определяется число наблюдений в каждой градации ni, которое для дальнейшей обработки должно быть не менее 100. Если ni <100, то значение Сфi , считается ориентировочным.
Фоновые концентрации загрязняющих веществ
в атмосферном воздухе
Слайд 59Данные подфакельных наблюдений группируются по зонам, которые соответствуют расстояниям от
источника выбросов. Количество наблюдений в каждой зоне должно быть не
менее 200. Данные для каждой зоны делятся на две градации по скорости ветра: i=0 соответствует скорости ветра 0÷2 м/с; i=1 соответствует скорости ветра 3÷ W* м/с.
Отдается предпочтение Сф, полученным по подфакельным измерениям, для тех участков города, где их величины больше, чем Сф, рассчитанные по данным наблюдений на стационарных постах.
Методы определения фоновых концентраций
Фоновая концентрация Сф, может определяться одним из статистических расчетных методов либо графически.
Расчетный метод
При определении Сф расчетным методом для каждой градации i сначала вычисляется среднее значение концентрации по формуле:
где - сумма всех значений концентраций, попавших в градацию i.
Фоновые концентрации загрязняющих веществ
в атмосферном воздухе
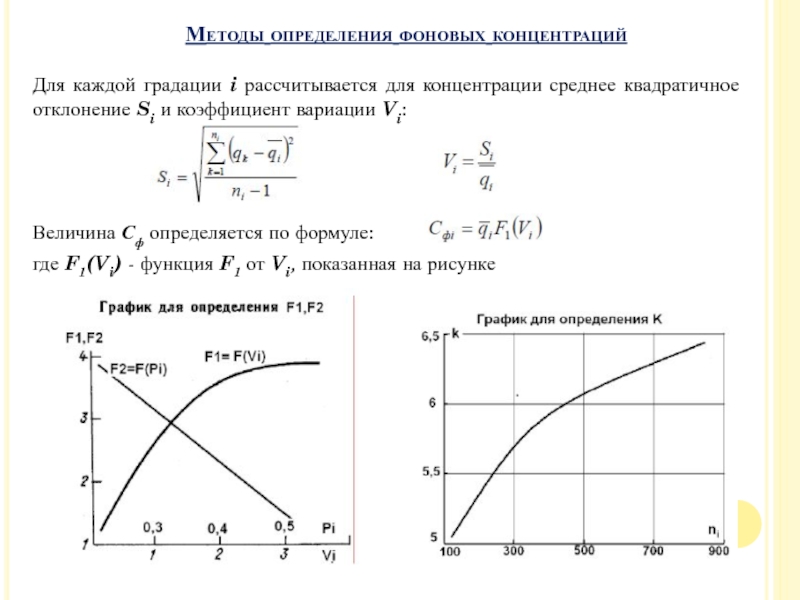
Слайд 60Для каждой градации i рассчитывается для концентрации среднее квадратичное отклонение
Si и коэффициент вариации Vi:
Величина Сф определяется по формуле:
где F1(Vi)
- функция F1 от Vi, показанная на рисунке
Методы определения фоновых концентраций
Слайд 61Существуют упрощенные методы определения Сф, которые заключаются в следующем:
а) для
каждой градации i определяется число наблюдений, в которых значение концентрации
qk превышало среднюю концентрацию в данной градации , а также повторяемость Рi случаев превышения среднего значения :
Фоновая концентрация определяется по формуле:
где F2(Рi) - функция F2 от Рi, показанная на предыдущем рисунке.
б) Метод «размаха». Среднеквадратичное отклонение рассчитывается по приближенной формуле:
где qmax и qmin – максимальная и минимальная концентрация в градации; k – коэффициент, зависящий от числа наблюдений
Методы определения фоновых концентраций
Слайд 62Графический метод
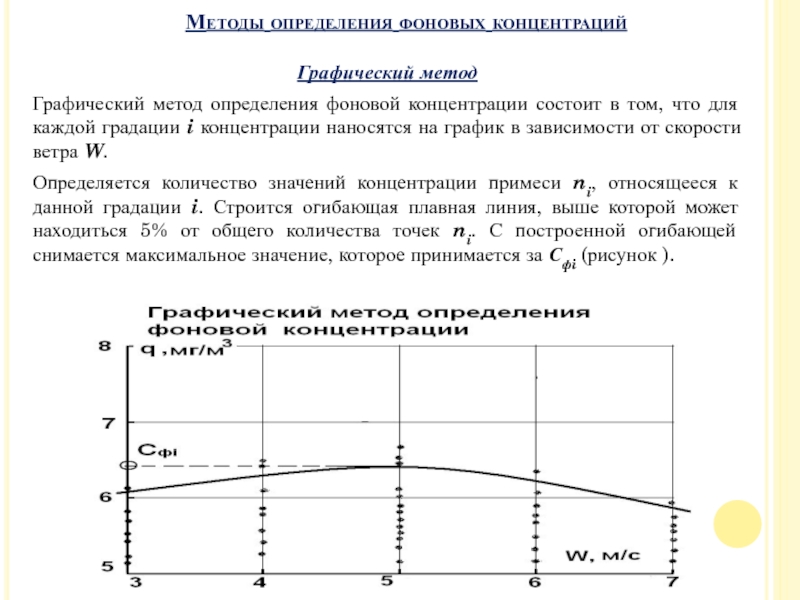
Графический метод определения фоновой концентрации состоит в том, что
для каждой градации i концентрации наносятся на график в зависимости
от скорости ветра W.
Определяется количество значений концентрации примеси ni, относящееся к данной градации i. Строится огибающая плавная линия, выше которой может находиться 5% от общего количества точек ni. С построенной огибающей снимается максимальное значение, которое принимается за Сфi (рисунок ).
Методы определения фоновых концентраций
Слайд 63Оценки значимости различий Сф и исключение вклада предприятия
Для проведения оценки
значимости различий Сф для различных градаций рассчитываются значения фоновой концентрации:
- среднее по пяти градациям и - среднее по четырем градациям (без градации i = 0 для скорости ветра 0÷2 м/с):
где - сумма пяти произведений Сфi для каждой градации на количество измерений в данной градации ni.
Если максимальное и минимальное значение Сфi при i=0,1,2,3,4 удовлетворяют неравенству:
то для такого поста в качестве Сф принимается значение независимо от направления и скорости ветра.
Методы определения фоновых концентраций
Слайд 64Если предыдущее условие не выполняется, но минимальное и максимальное значения
Сфi при i=1,2,3,4 удовлетворяют неравенству:
то для данного поста принимаются два
значения фона: одно - для градации скорости ветра 0÷2 м/с, другое - для скорости ветра 3÷W* м/с (значение ).
Когда оба неравенства не выполняются, Сф представляется пятью значениями.
Для учета суммации вредного действия нескольких загрязняющих веществ допускается определение единой величины фона по этим веществам. При этом для каждого пункта наблюдения и момента времени концентрация n веществ приводится к концентрации наиболее распространенного из них вещества.
Например, при суммации воздействия SO2 и NO2:
Методы определения фоновых концентраций
Слайд 65Дальнейшая обработка результатов проводится так же, как и в случае
одного вещества.
При проектировании промышленных предприятий и установлении ПДВ данные
о распределении фоновой концентрации по территории населенного пункта представляются в табличной форме.
В отдельных случаях можно ограничиться средним значением по городу. Для этого вычисляется среднее значение по городу для каждой градации скорости и направления ветра. Для тех постов, для которых в рассматриваемой градации Сфi отличается от среднего по городу менее, чем на 25%, оно заменяется на среднюю по городу величину .
При установлении ПДВ для реконструируемых или действующих предприятий исключение из Сф вклада рассматриваемого предприятия производится по формулам:
где Сф′ - фоновая концентрация без учета рассматриваемого предприятия;
С – максимальная концентрация, создаваемая предприятием в месте размещения поста.
Методы определения фоновых концентраций
Слайд 66Лекция 15. Теплообмен излучением
Основные определения
Излучение – это процесс распространения электромагнитных
волн, испускаемых телом при преобразовании внутренней энергии тела в результате
внутримолекулярных и внутриатомных возмущений в лучистую энергию.
Лучистая тепловая энергия – энергия колебаний непрерывного электромагнитного поля в интервале длин волн λ от 0,4…0,8 мкм (видимое излучение) до 0,8 мкм…0,8 мм – невидимое (инфракрасное или тепловое) излучение.
Лучеиспускание – процесс превращения внутренней энергии тела в лучистую энергию. Лучеиспускание может быть непрерывным (0<λ>∞) или селективным (отдельные участки спектра для некоторых газов и паров). Лучеиспускание может быть диффузным (энергия излучается равномерно по всем направлениям) или направленным.
Перенос лучистой энергии – процесс ее распространения, определяемый физическими свойствами среды и спектральным составом излучения.
Слайд 67Основные определения
Поглощение – это процесс превращения части лучистой энергии во
внутреннюю энергию тела.
Отражение лучистой энергии от поверхности тела может быть
диффузным (равномерным во всех направлениях) и зеркальным (по законам геометрической оптики).
Лучистый теплообмен – совокупность процессов испускания, переноса, поглощения, отражения и пропускания теплового излучения.
Равновесный теплообмен – лучистый теплообмен между телами одинаковой температуры, при этом такое равновесие называют динамическим.
Замечание: Излучение электромагнитных волн свойственно всем телам. Для большинства твердых и жидких тел спектр излучения непрерывный. Это значит, что эти тела излучают (и поглощают) лучи всех длин волн. Распространение энергии в спектре излучающего тела определяется его температурой.
Лучистый поток – это общее количество лучистой энергии, испускаемой телом в единицу времени Q, Вт.
Слайд 68Основные определения
Поверхностная плотность потока – это поток излучения Q, проходящий
через единицу поверхности в пределах телесного угла 2π.
Монохроматическое излучение (Qλ)
– излучение в достаточно узком интервале длин волн.
Интенсивность или спектральная плотность потока излучения (Jλ) –отношение плотности потока монохроматического излучения в малом интервале длин волн λ к этому интервалу.
Собственное излучение – излучение, которое зависит от только от свойств и температуры тела.
Падающее излучение – излучение, которое тело получает от внешнего источника.
Слайд 69Основные законы теплового излучения
Закон Планка
Закон Планка устанавливает зависимость между
спектральной плотностью потока излучения Jλ,0 Вт/(м2*м), длиной волны λ и
температурой Т:
Здесь С1=2πhc02=3,7418*10-16 Вт*м2; С2=hc0/k=0,014387 м*К, где h = 6,625*10-34 Дж*с – постоянная Планка; k = 1,38*10-23 Дж/К – постоянная Больцмана; c0 - скорость света в вакууме.
Индекс «0» означает абсолютно черное тело.
Постоянная Планка h устанавливает соотношение между энергией е, излучаемой одним квантом, и частотой излучения ν, е=hν.
Постоянная Больцмана k устанавливает связь между температурой Т и внутренней энергией излучения u, u=kT.
Слайд 70Основные законы теплового излучения
Закон смещения Вина
На основе закона Планка
устанавливается взаимосвязь между температурой излучающего тела T и длиной волны
λmax, соответствующей максимальной спектральной плотности потока излучения Jλ,0 .
λmax Т=0,898 мм*К
Данное уравнение и есть математическое выражение закона смещения Вина!
С повышением температуры, согласно данному уравнению, длина волны, соответствующая максимальной плотности потока излучения, смещается в сторону более коротких волн.
Определяя из него величину λmax и подставляя ее в формулу Планка, получим величину максимальной плотности потока излучения Jλ,0,max при температуре Т, Вт/(м2*м):
Слайд 71Основные законы теплового излучения
Закон Стефана-Больцмана
Этот закон устанавливает связь между
плотностью потока интегрального полусферического излучения абсолютно черного тела Е0, Вт/м2
и его температурой:
Е0 = С0 (Т/100)4
где С0=σ0108=5,6686 Вт/(м2*К4) – коэффициент излучения абсолютно черного тела.
Для серых тел при той же температуре Е < Е0. Плотность потока интегрального излучения серого тела можно определить по уравнению, Вт/м2:
Е = εЕ0 = С(Т/100)4
где С = εЕ0 – коэффициент излучения серого тела, Вт/(м2*К4), ε - степень черноты серого тела.
Слайд 72Закон Ламберта
Этот закон определяет значение плотности потока Еφ в зависимости
от его направления по отношению к равномерно излучающей поверхности тела.
Наибольшей плотностью обладает поток излучения по нормали к поверхности, его называют яркостью излучения и обозначают Еn.
Плотность потока по остальным направлениям Еφ определяется по формуле:
Еφ = Еn cosφ, Еn = Е/π
где φ – угол между направлением излучения и нормалью.
Плотность излучения в полусферическое пространство Е в π раз больше плотности излучения по нормали к поверхности в единичном телесном угле Еn .
Подставляя Еn = Е/π получим:
Еφ = (Е/π)cosφ
Закон Ламберта строго справедлив для абсолютно черных тел и хорошо выполняется для диэлектриков и окисленных поверхностей металлов при угле φ <60о.
Плотность потока излучения на сфере радиусом R0 около диффузно излучающего точечного источника мощностью Q равна:
Слайд 73Закон Кирхгофа
Этот закон устанавливает связь между степенью черноты ε и
поглощающей способностью А серых тел. Рассмотрим лучистый теплообмен между параллельно
расположенными неограниченными пластинами: серой – с температурой Т и поглощающей способностью А и абсолютно черной с температурой Т0. Примем Т > Т0, тогда плотность теплового потока, передаваемого серым телом черному равна:
q = E - Е0 А
где Е – плотность потока излучения серого тела, полностью поглощенная абсолютно черным телом; Е0 А - плотность потока излучения абсолютно черного тела, поглощенная серым телом.
Отраженный от серого тела лучистый поток Е0 (1-А) полностью поглощается абсолютно черным телом. После выравнивания температур тел, участвующих в лучистом теплообмене (Т = Т0), имеет место тепловое равновесие q=0, откуда
E/А=Е0
Последнее уравнение составляет содержание закона Кирхгофа: отношение плотности потока излучения Е к его поглощательной способности А одинаково для всех тел и равно плотности потока излучения абсолютно черного тела при той же температуре.
Слайд 74Я не сумел списать на экзамене «ТЕПЛОМАССООБМЕН В БИОСФЕРЕ»