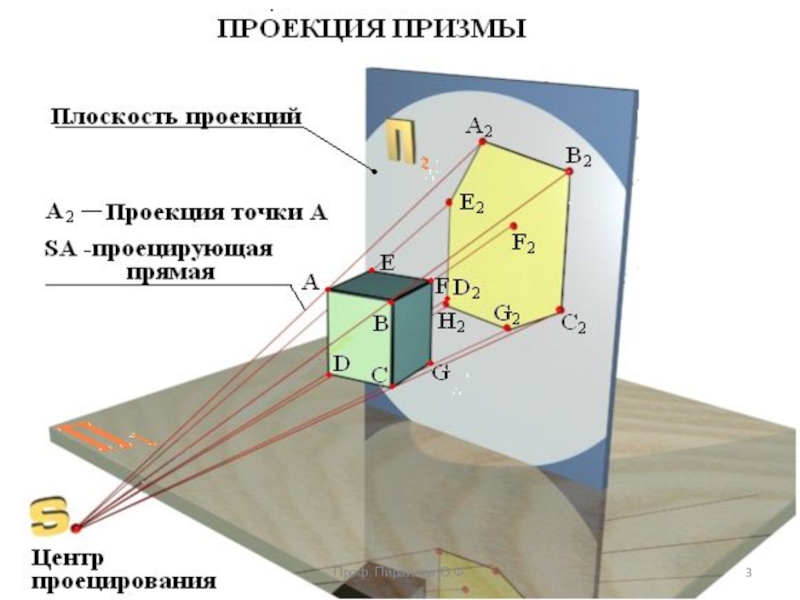
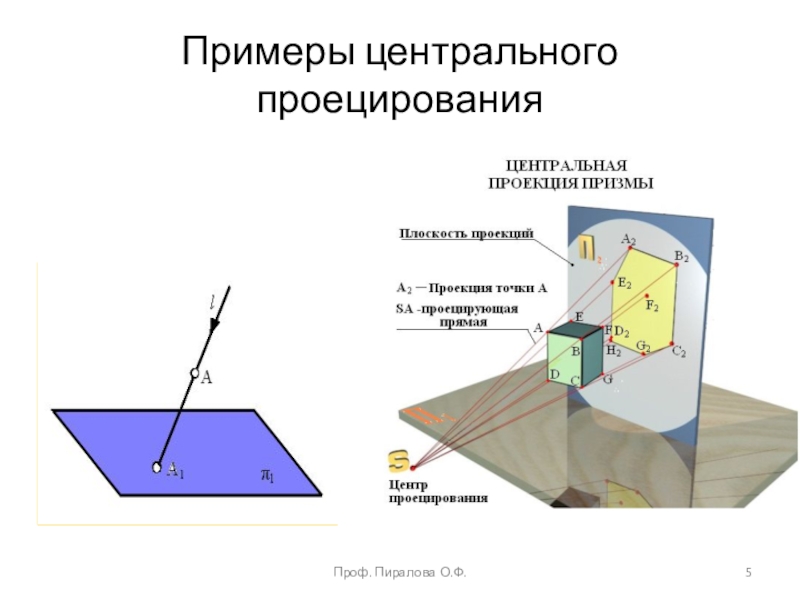
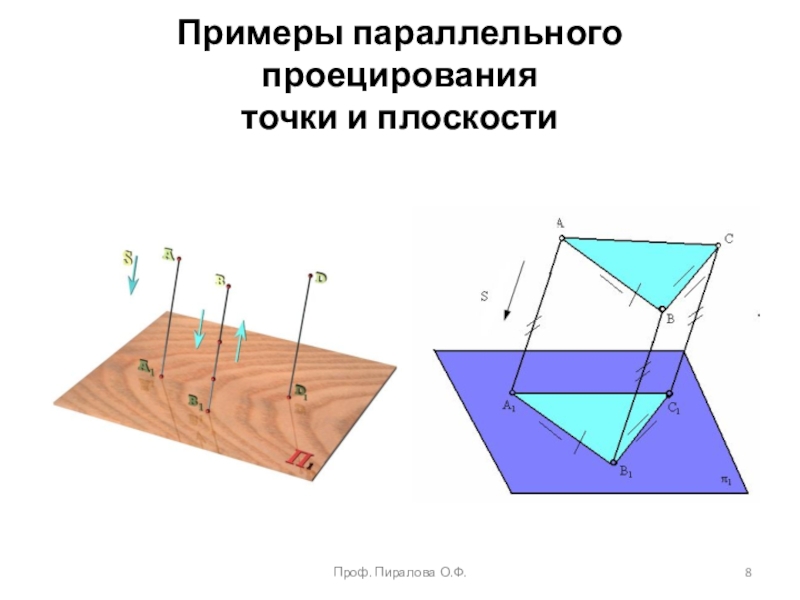
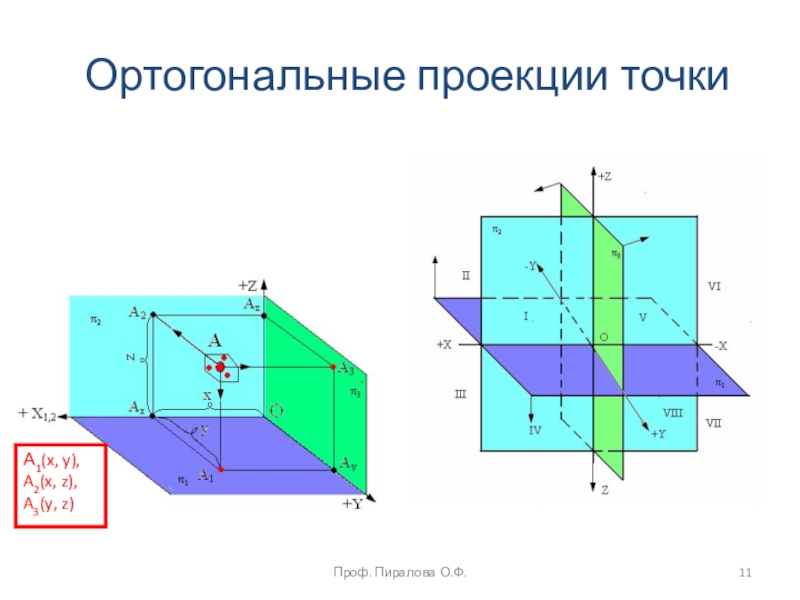
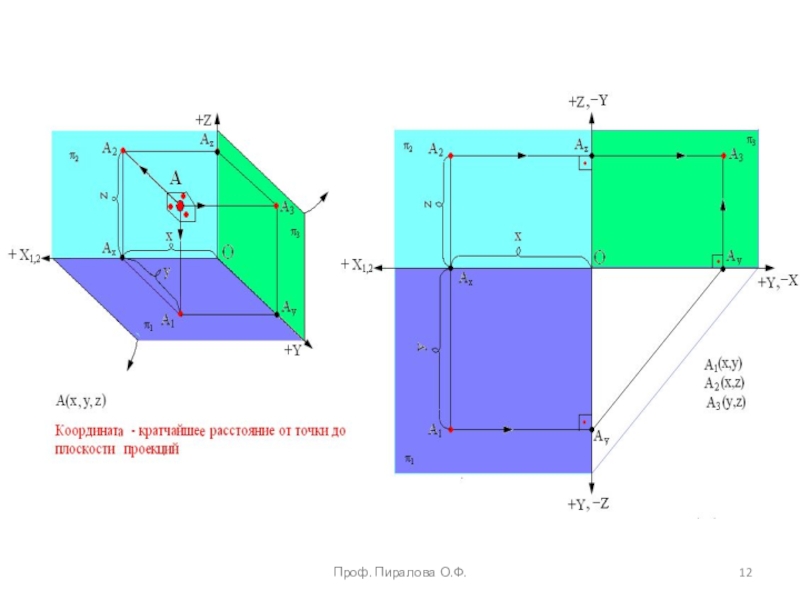
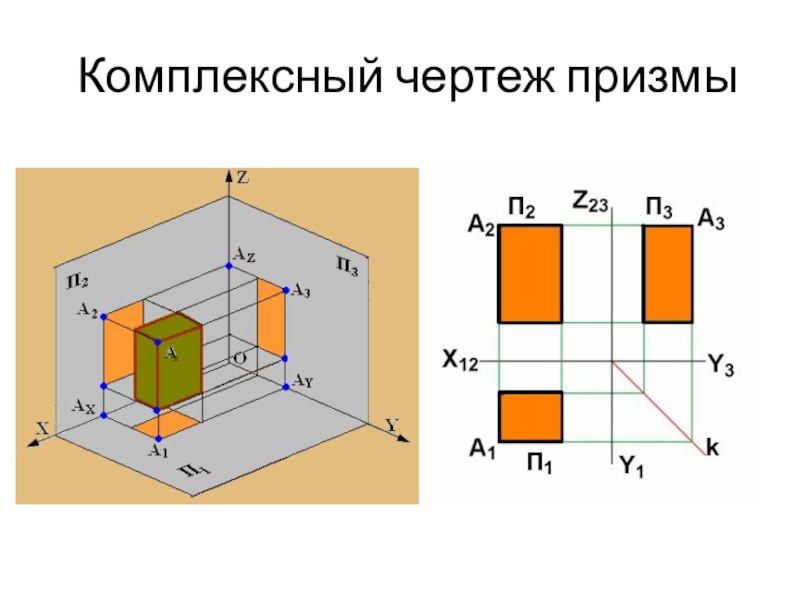
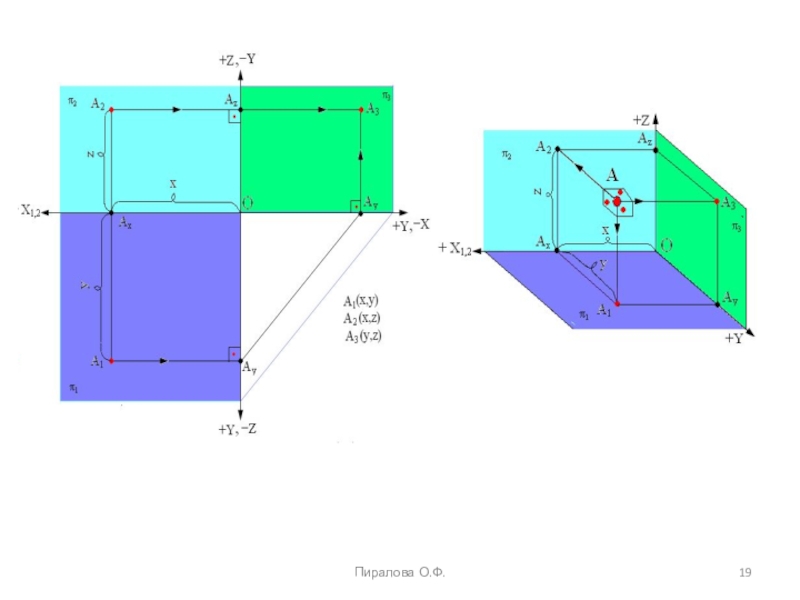
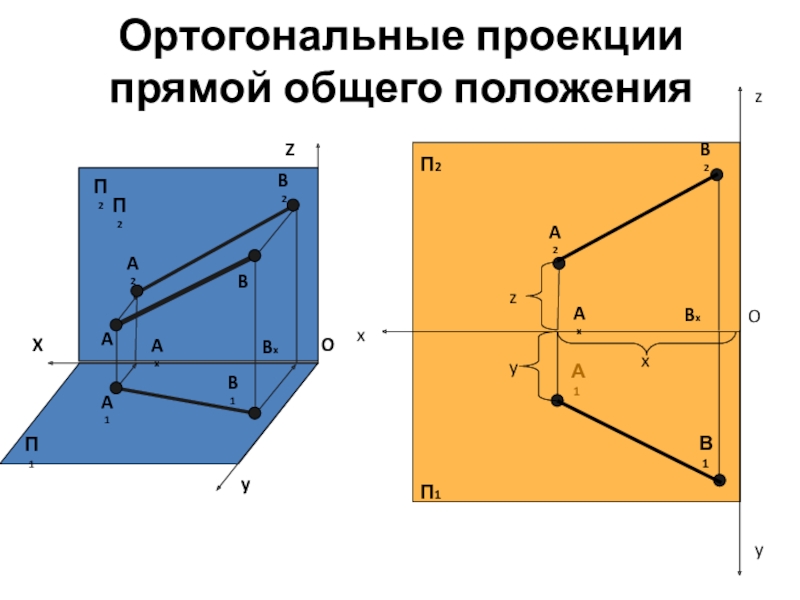
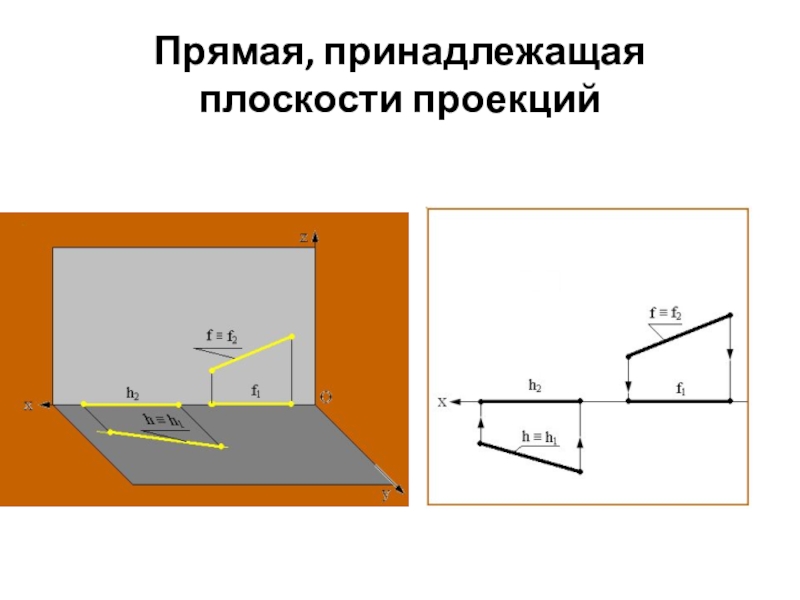
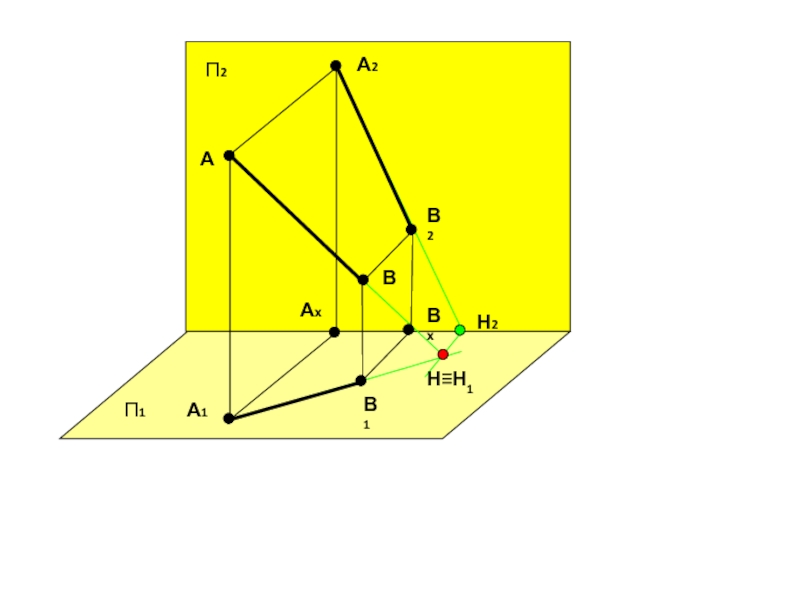
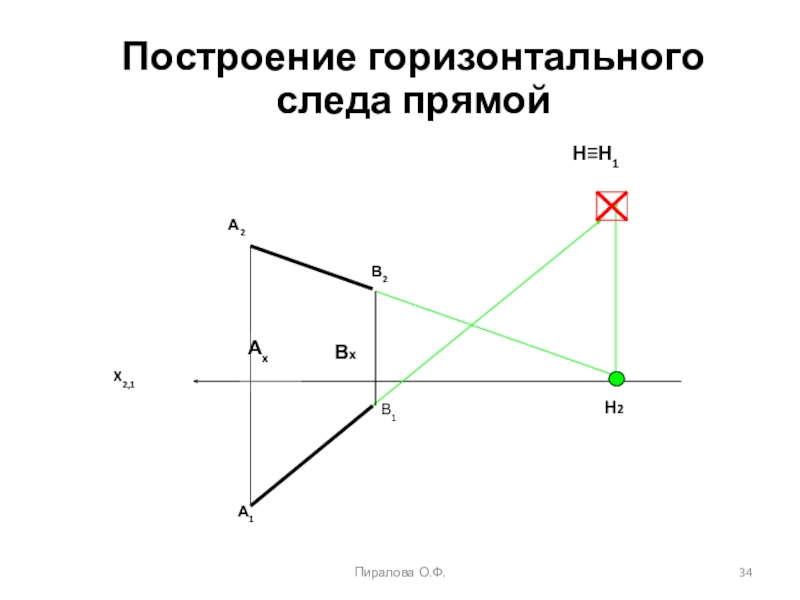
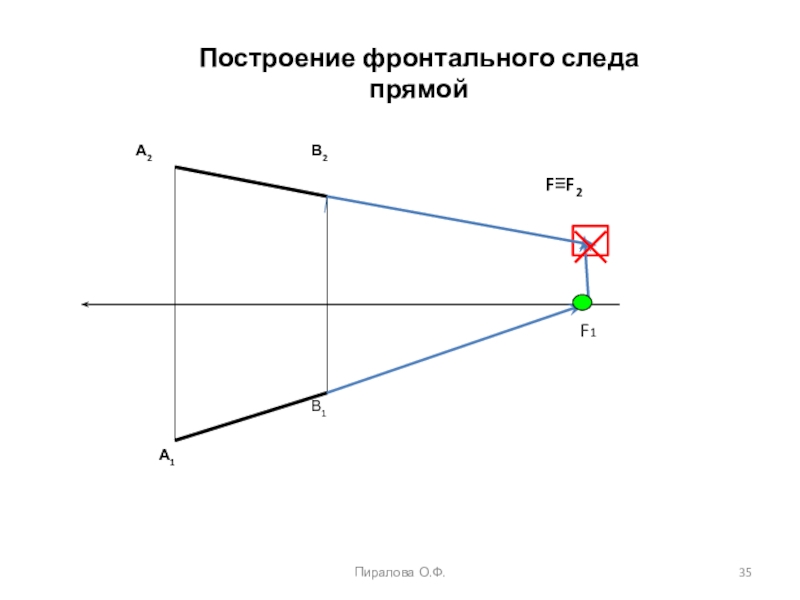
projectio – бросание вперед). Проекция – это отображение образа (предмета)
на плоскость проекций. Идею метода можно рассмотреть на примере проецирования любого образа. Спроецируем призму. Методы проецирования подразделяют на центральное и параллельное.Проф. Пиралова О.Ф.