Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛЕКЦИЯ № 1 Колебания ( 2 часа)
Содержание
- 1. ЛЕКЦИЯ № 1 Колебания ( 2 часа)
- 2. Понятие о колебательных процессах. Кинематика гармонических колебаний.
- 3. Физические процессы, характеризующиеся тойили иной степенью повторяемости, называютсяколебаниями.Колебания сопровождаются попеременнымпревращением энергии одного вида в энергиюдругого вида.
- 4. Физическая природа колебаний может быть разной – различают механические, электромагнитные, электромеханические и другие колебания.
- 5. Виды колебаний:1. Периодические (гармонические и негармонические) и
- 6. Колебания называют периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
- 7. Гармоническими называются периодические колебания, при которых смещение
- 8. Слайд 8
- 9. Периодом колебания Т называется наименьший промежуток времени,
- 10. Частотой колебаний называется величина обратная периоду колебаний.
- 11. Гармонические колебания - это колебания, описываемые дифференциальными
- 12. Скорость Ускорение
- 13. Графики координаты x(t), скорости υ(t) и ускорения a(t) тела, совершающего гармонические колебания.
- 14. № 1 . Материальная точка совершает гармонические
- 15. № 2. На рисунках изображены зависимости от
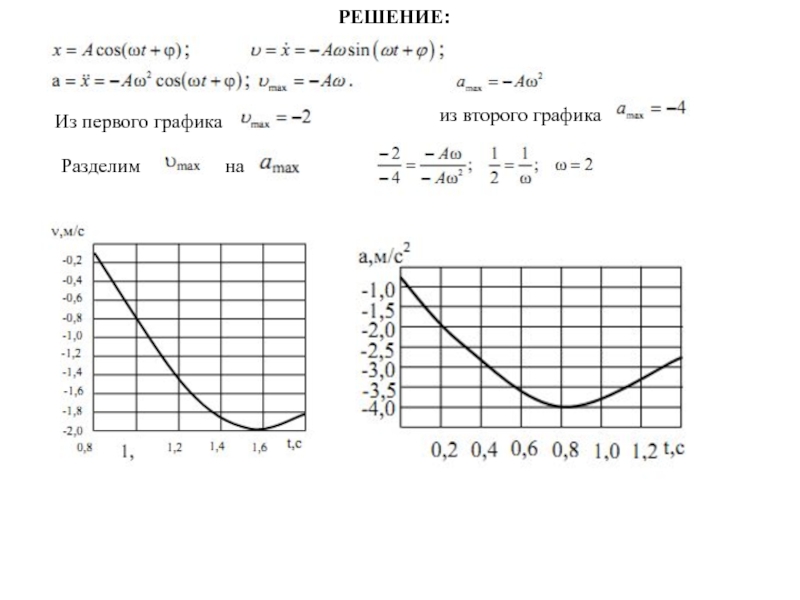
- 16. Из первого графика из второго графика Разделим на РЕШЕНИЕ:
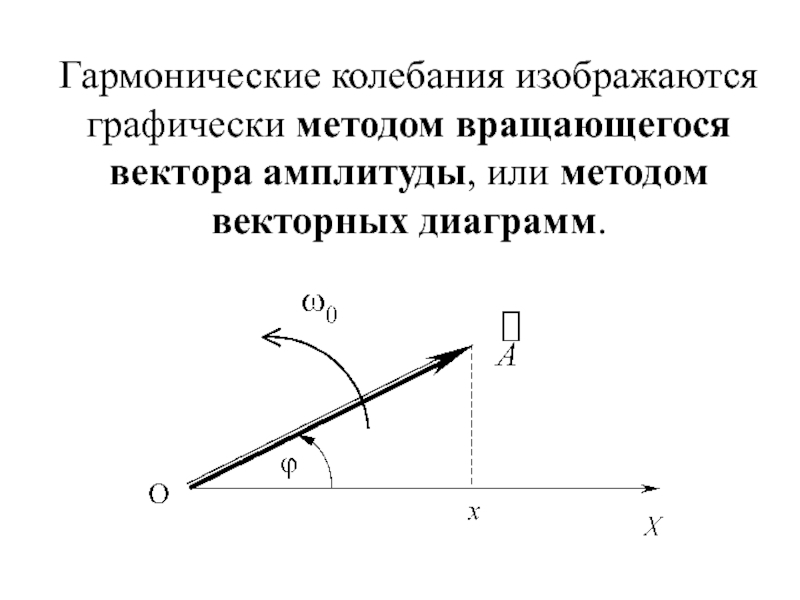
- 17. Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.
- 18. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР - система с одной степенью свободы, колебания которой описываются уравнением вида
- 19. Примеры гармонического осциллятора Пружинный маятник Физический маятник Математический маятник Электрический колебательный контур
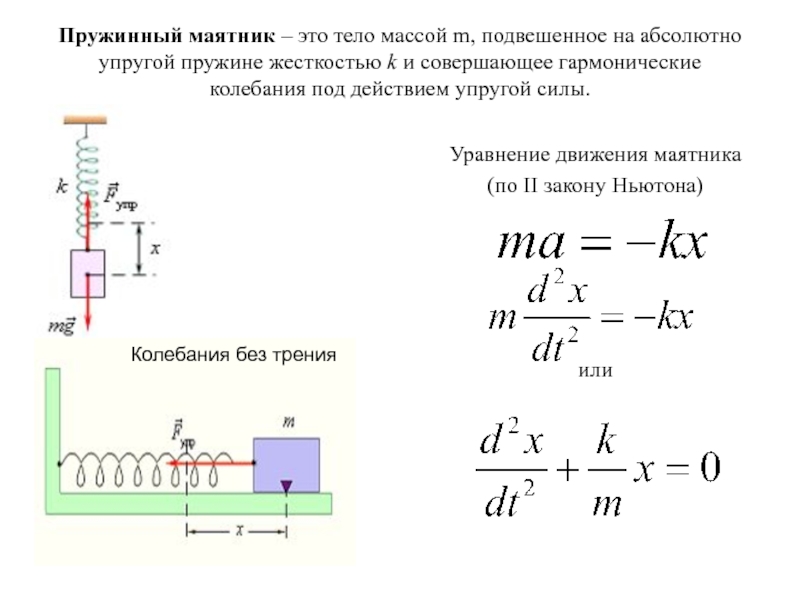
- 20. Уравнение движения маятника (по II закону Ньютона)илиПружинный
- 21. Сравним это уравнение с уравнением движения гармонического осциллятора. Получим значение циклической частоты и периода.
- 22. Потенциальная энергия пружинного маятника
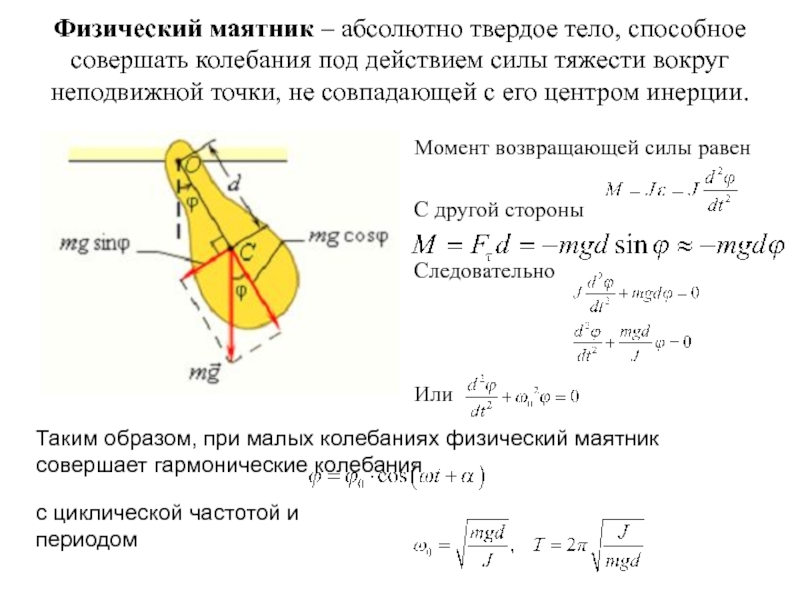
- 23. Физический маятник – абсолютно твердое тело, способное
- 24. Математический маятник – материальная точка, подвешенная на
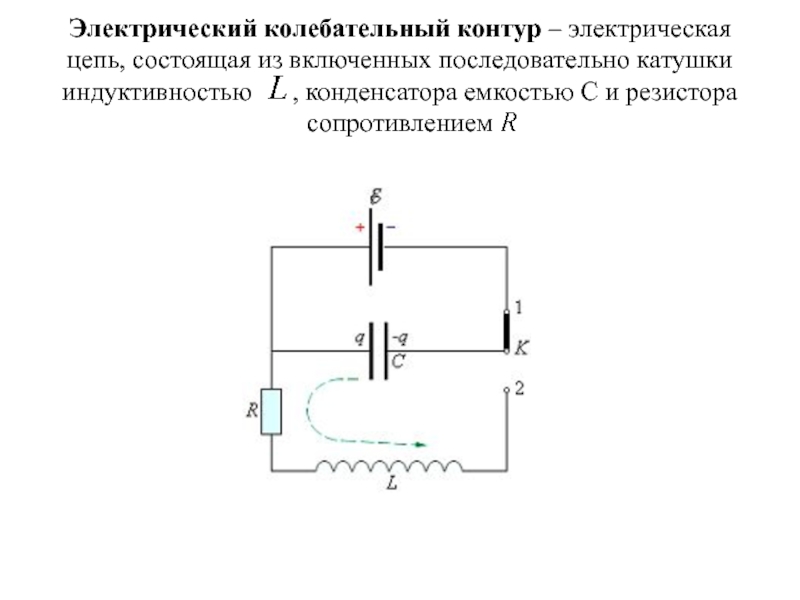
- 25. Электрический колебательный контур – электрическая цепь, состоящая
- 26. Заряд совершает гармонические колебания по закону формулаТомсона- циклическая частота (собственная частота контура)
- 27. Слайд 27
- 28. Сложение колебаний одного направления и одинаковой частоты Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:
- 29. № 3. Складываются два гармонических колебания одного
- 30. РЕШЕНИЕ: Графически амплитуды складываемых колебаний можно
- 31. № 4. Складываются два гармонических колебания одного
- 32. № 5. Складываются два гармонических колебания одного
- 33. Биения Биения – периодическиеизменения
- 34. Сложение взаимно-перпендикулярных гармонических колебаний одинаковой частоты.Эллиптически поляризованные
- 35. Рассмотрим некоторые частные случаи, представляющие физический интерес:
- 36. 2. Циркулярно поляризованные колебания или колебания, поляризованные
- 37. Замкнутые траектории,прочерчиваемые точкой,совершающейодновременно два взаимно- перпендикулярныхколебания, называютсяфигурами
- 38. № 6. Точка М одновременно колеблется по
- 39. Свободные затухающие колебания -колебания, амплитуды которых из-за
- 40. временя релаксации логарифмический декремент затухания добротность колебательной системы
- 41. Свободные затухающие колебания в электрическом колебательном контуреКоэффициент затуханияКолебания заряда совершаются по законуЧастотаДобротность колебательного контура
- 42. Колебания, возникающие под действием внешней периодически изменяющейся
- 43. Процесс установления вынужденных незатухающих колебаний. Процесс установления
- 44. Слайд 44
- 45. Системы, в которых незатухающие колебания возникают в
- 46. Скачать презентанцию
Понятие о колебательных процессах. Кинематика гармонических колебаний. Амплитуда, частота, фаза колебаний. Сложение колебаний. Комплексная форма представления колебаний. Векторные диаграммы. Гармонический осциллятор. Маятник, груз на пружине, колебательный контур. Свободные затухающие
Слайды и текст этой презентации
Слайд 2Понятие о колебательных процессах. Кинематика гармонических колебаний. Амплитуда, частота, фаза
Слайд 3Физические процессы, характеризующиеся той
или иной степенью повторяемости, называются
колебаниями.
Колебания сопровождаются попеременным
превращением
энергии одного вида в энергию
другого вида.
Слайд 4Физическая природа колебаний может быть разной – различают механические, электромагнитные,
электромеханические и другие колебания.
Слайд 5Виды колебаний:
1. Периодические (гармонические и негармонические) и непериодические.
2. Собственные, затухающие,
вынужденные, параметрические и автоколебания.
3. Механические, электромагнитные и др.
Слайд 6Колебания называют периодическими, если значения физических величин, изменяющихся в процессе
колебаний, повторяются через равные промежутки времени.
Слайд 7Гармоническими называются периодические колебания, при которых смещение точки от положения
равновесия со временем меняется по закону косинуса (или синуса).
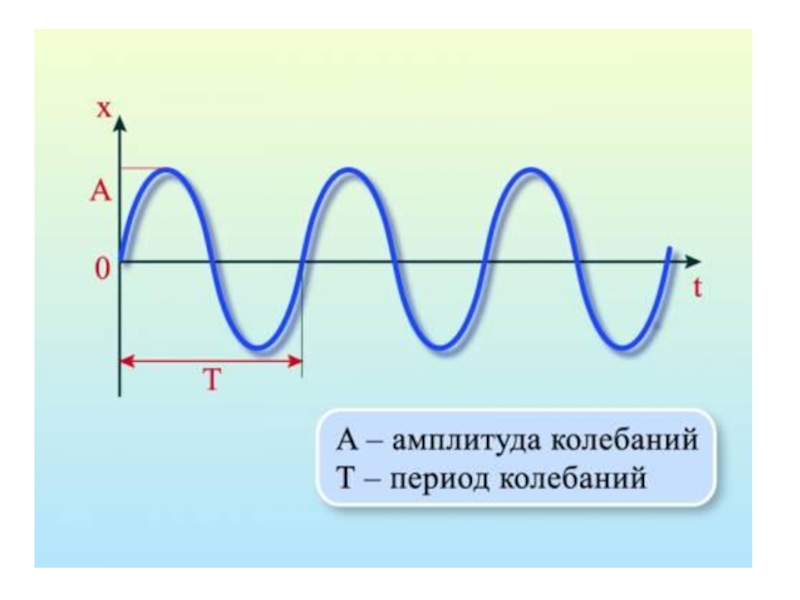
Слайд 9Периодом колебания Т называется наименьший промежуток времени, за который совершается
одно полное колебание.
Слайд 10Частотой колебаний называется величина обратная периоду колебаний. Наибольшая величина отклонения
колеблющейся точки от своего начального положения называется амплитудой колебаний A.
Слайд 11Гармонические колебания - это колебания, описываемые дифференциальными уравнениями вида
, решением которых является
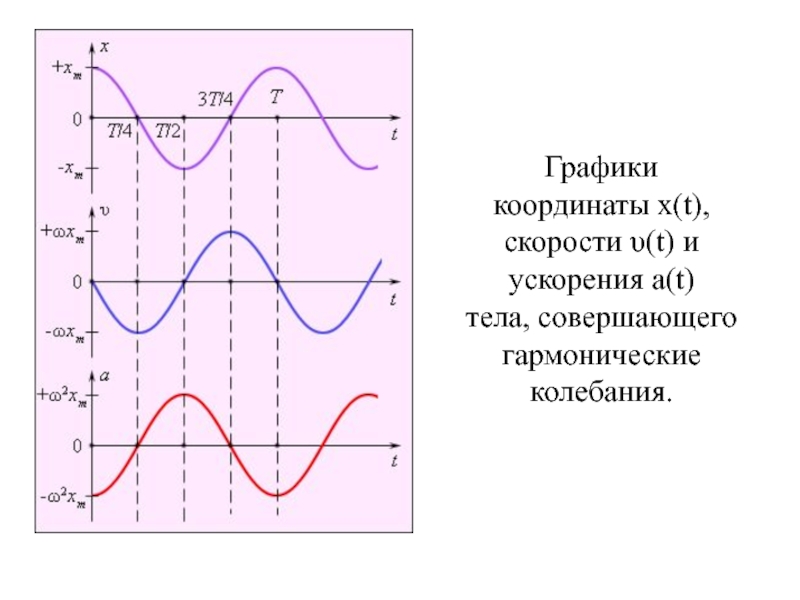
гармоническое колебание .
Слайд 13Графики координаты x(t), скорости υ(t) и ускорения a(t) тела, совершающего
гармонические колебания.
Слайд 14№ 1 . Материальная точка совершает гармонические колебания по закону
Максимальное значение ускорения точки равно…
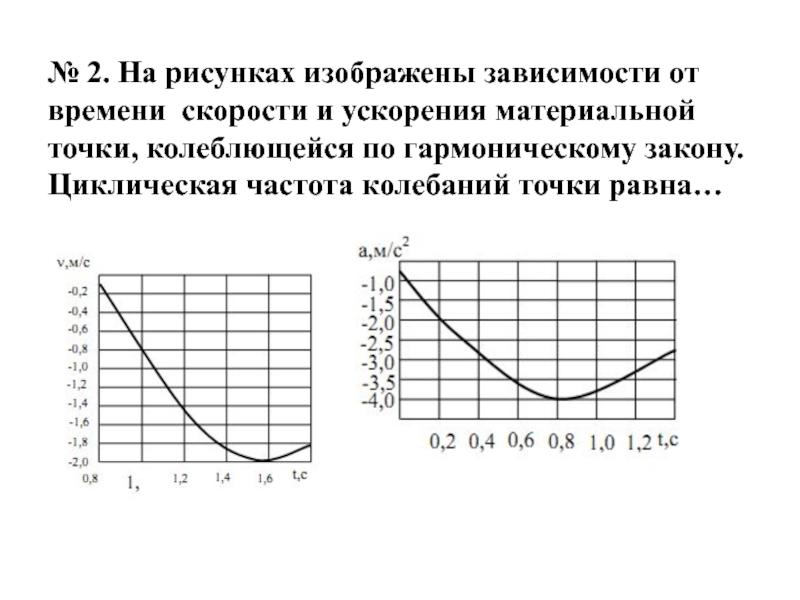
Слайд 15№ 2. На рисунках изображены зависимости от времени скорости и
ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний
точки равна…
Слайд 17Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом
векторных диаграмм.
Слайд 18ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР - система с одной степенью свободы, колебания которой
описываются уравнением вида
Слайд 19
Примеры гармонического осциллятора
Пружинный маятник
Физический маятник
Математический маятник
Электрический колебательный
контур
Слайд 20Уравнение движения маятника
(по II закону Ньютона)
или
Пружинный маятник – это
тело массой m, подвешенное на абсолютно упругой пружине жесткостью k
и совершающее гармонические колебания под действием упругой силы.Колебания без трения
Слайд 21Сравним это уравнение с уравнением движения гармонического осциллятора. Получим значение
циклической частоты и периода.
Слайд 23Физический маятник – абсолютно твердое тело, способное совершать колебания под
действием силы тяжести вокруг неподвижной точки, не совпадающей с его
центром инерции.Момент возвращающей силы равен
С другой стороны
Следовательно
Или
Таким образом, при малых колебаниях физический маятник совершает гармонические колебания
с циклической частотой и периодом
Слайд 24Математический маятник – материальная точка, подвешенная на невесомой и нерастяжимой
нити длиной l и совершающая колебания в вертикальной плоскости под
действием силы тяжести Р.При малых углах отклонения можно считать .
Возвращающая сила
Уравнение движения
или
Частота и период
Слайд 25Электрический колебательный контур – электрическая цепь, состоящая из включенных последовательно
катушки индуктивностью , конденсатора емкостью С и резистора
сопротивлением
Слайд 26Заряд совершает гармонические колебания по закону
формулаТомсона
- циклическая частота (собственная частота
контура)
Слайд 28Сложение колебаний одного направления и одинаковой частоты
Амплитуда результирующего колебания
зависит от разности фаз складываемых колебаний:
Слайд 29№ 3. Складываются два гармонических колебания одного направления с одинаковыми
периодами и равными амплитудами Ао. При разности фаз
амплитуда результирующего колебания равна…
Слайд 30РЕШЕНИЕ: Графически амплитуды складываемых колебаний можно изобразить так: Амплитуда результирующего колебания: Вычисления
проводим по теореме косинусов: по условию тогда Ответ:
.
Слайд 31№ 4. Складываются два гармонических колебания одного направления с одинаковыми
частотами и равными амплитудами А0. При разности фаз ∆φ=0 амплитуда
результирующего колебания равна...
Слайд 32№ 5. Складываются два гармонических колебания одного направления с одинаковыми
частотами и равными амплитудами A0 . При разности фаз
амплитуда результирующего колебания равна...
Слайд 33 Биения
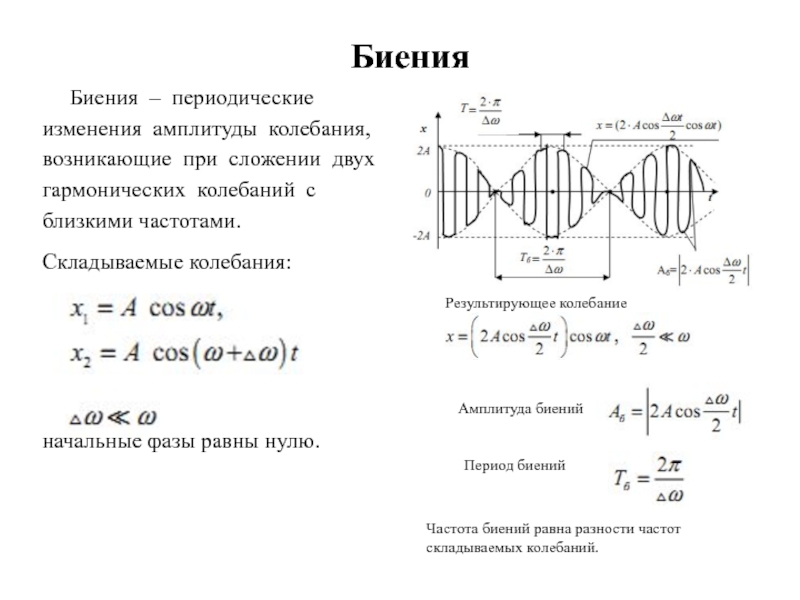
Биения – периодические
изменения амплитуды колебания,
возникающие
при сложении двух
гармонических колебаний с
близкими частотами.
Складываемые колебания:
начальные фазы равны
нулю. Результирующее колебание
Амплитуда биений
Период биений
Частота биений равна разности частот складываемых колебаний.
Слайд 34Сложение взаимно-перпендикулярных гармонических колебаний одинаковой частоты.
Эллиптически поляризованные колебания
Складываемые колебания
Уравнение траектории результирующего колебания
Это – уравнение эллипса.
Эллиптически-поляризованные
колебания – колебания, в которых траектория результирующего колебания имеет форму эллипса.Ориентация эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз α .
Слайд 35Рассмотрим некоторые частные случаи, представляющие физический интерес:
1. Линейно поляризованные колебания
Если разность фаз
, то эллипс вырождается в отрезок
прямой , где знак плюс
соответствует нулю и четным
значениям m, а знак минус — нечетным
значениям m.
Слайд 362. Циркулярно поляризованные колебания или колебания, поляризованные по кругу.
Если разность
фаз
, то уравнение примет вид .
Это уравнение эллипса, оси
которого совпадают с осями
координат, а его полуоси равны
соответствующим амплитудам.
Кроме того, если А=В, то эллипс
вырождается в окружность.
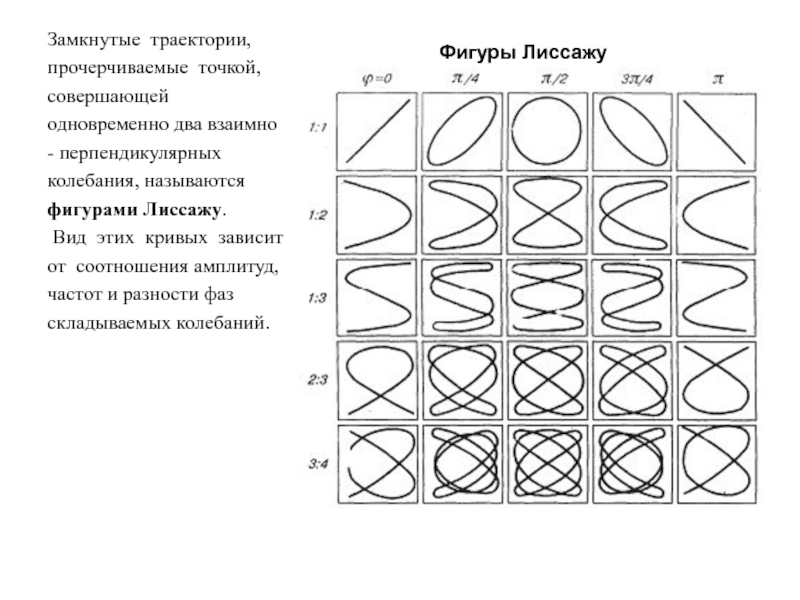
Слайд 37Замкнутые траектории,
прочерчиваемые точкой,
совершающей
одновременно два взаимно
- перпендикулярных
колебания, называются
фигурами Лиссажу.
Вид этих
кривых зависит
от соотношения амплитуд,
частот и разности фаз
складываемых колебаний.
Фигуры Лиссажу
Слайд 38№ 6. Точка М одновременно колеблется по гармоническому закону вдоль
осей координат ОХ и OY с одинаковыми амплитудами и одинаковыми
частотами. При разности фазтраектория точки М имеет вид…
Слайд 39Свободные затухающие колебания -
колебания, амплитуды которых из-за потерь энергии колебательной
системой с течением времени уменьшаются.
- амплитуда затухающих колебаний
- период затухающих
колебаний
Слайд 41Свободные затухающие колебания в электрическом колебательном контуре
Коэффициент затухания
Колебания заряда совершаются
по закону
Частота
Добротность колебательного контура
Слайд 42Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней
периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными
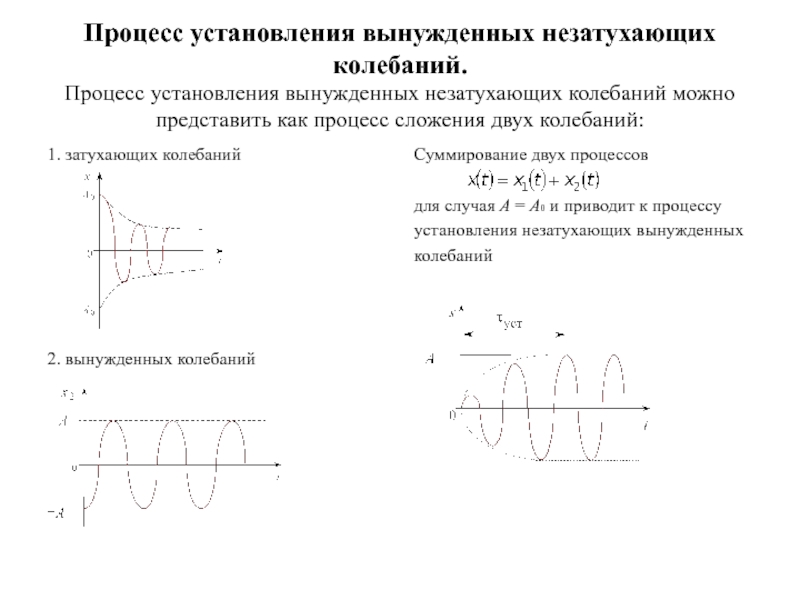
электромагнитными колебаниями. В общем виде дифференциальное уравнение вынужденных колебаний имеет вид:
Слайд 43Процесс установления вынужденных незатухающих колебаний. Процесс установления вынужденных незатухающих колебаний можно представить
как процесс сложения двух колебаний:
1. затухающих колебаний
2. вынужденных колебаний
Суммирование двух
процессов для случая A = A0 и приводит к процессу
установления незатухающих вынужденных
колебаний
Слайд 44
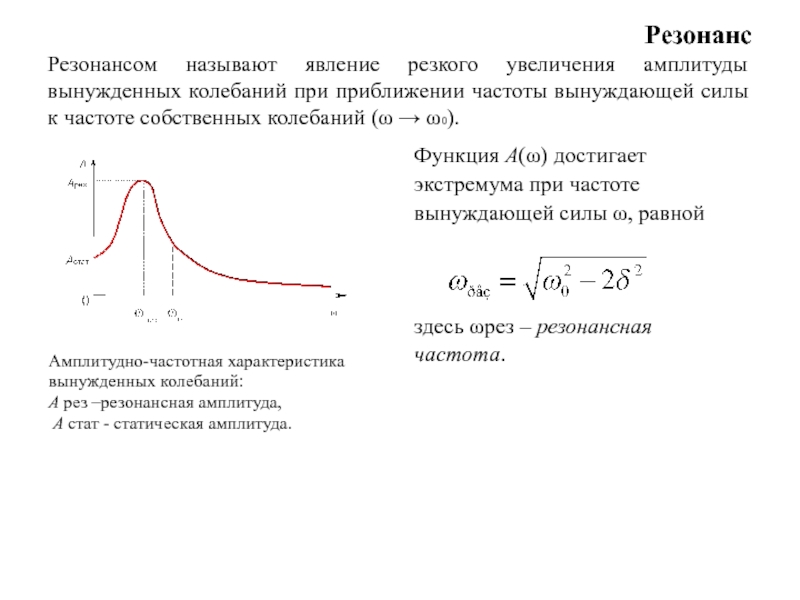
Резонанс Резонансом называют явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний ( 0).
Амплитудно-частотная характеристика
вынужденных колебаний:
A рез –резонансная амплитуда,
A стат - статическая амплитуда.
Функция A() достигает
экстремума при частоте
вынуждающей силы , равной
здесь рез – резонансная
частота.
Слайд 45Системы, в которых незатухающие колебания возникают в результате имеющейся у
таких систем способности самой регулировать поступление энергии от постоянного источника,
называются автоколебательными, а процесс незатухающих колебаний в таких системах–автоколебаниями.Часовой механизм с маятником.
