Лекция № 6

и системы
Тема 1.2 Авиагоризонты

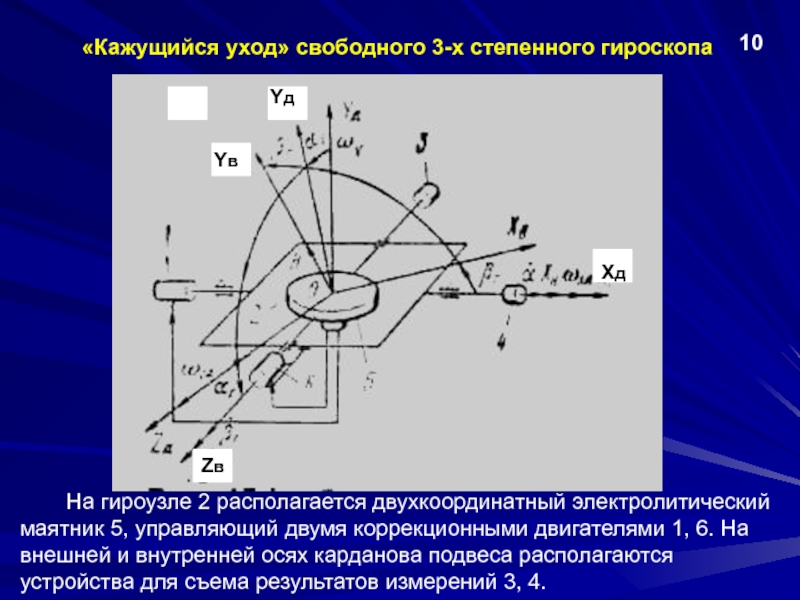
и гировертикали
 

Применение 3-х степенного гироскопа для измерения углов крена и тангажа

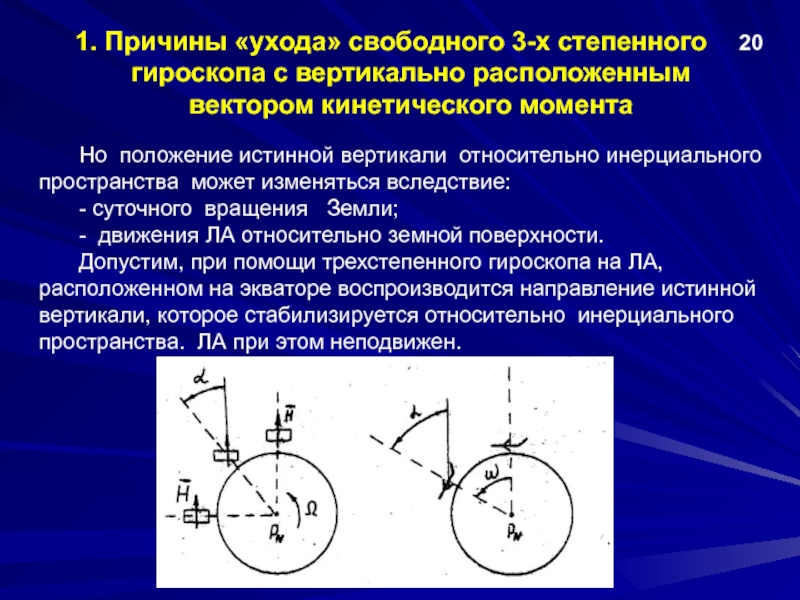
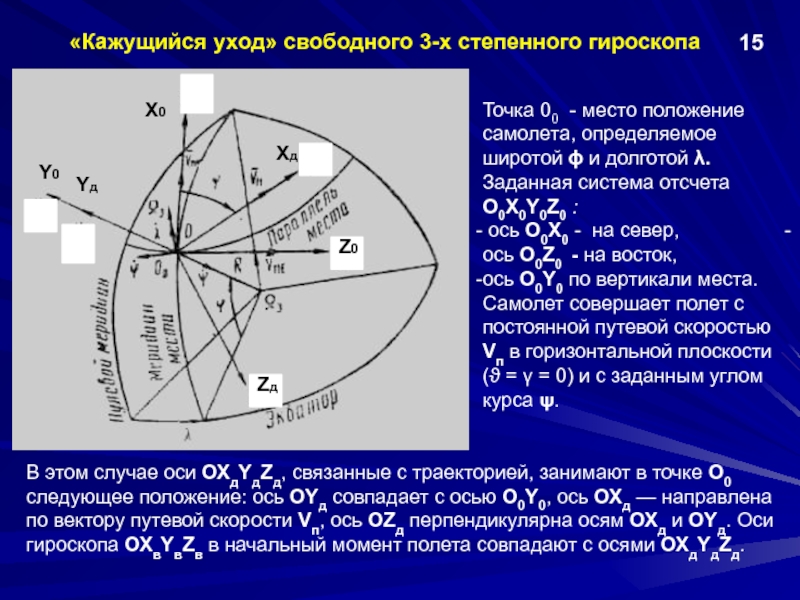
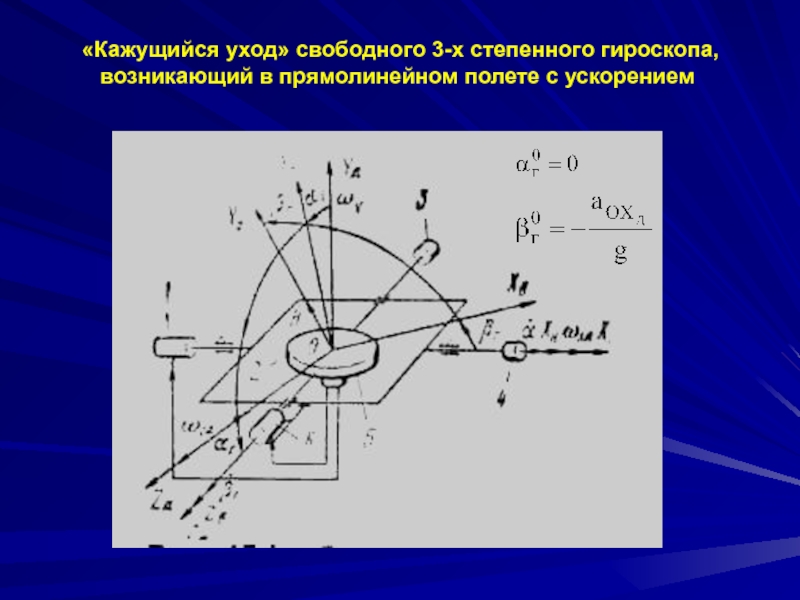
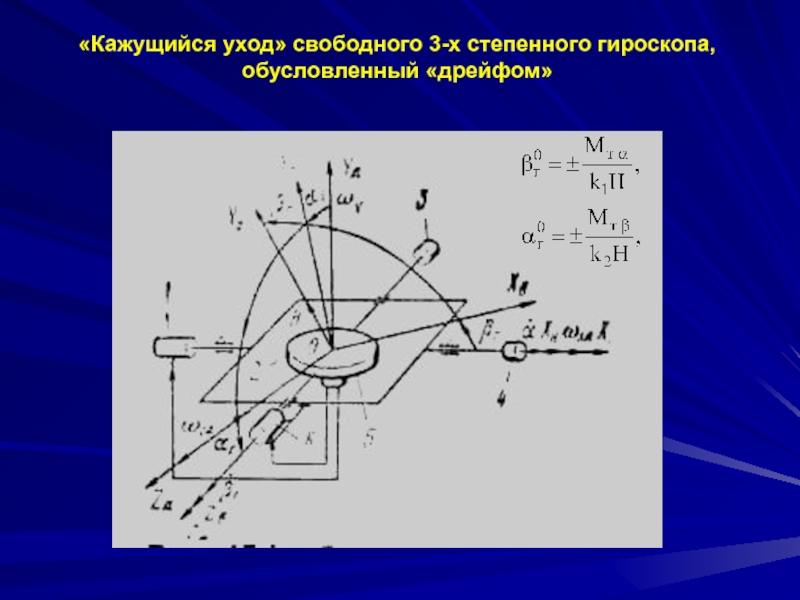
Причины «ухода» свободного 3-х степенного гироскопа с вертикально расположенным вектором кинетического момента
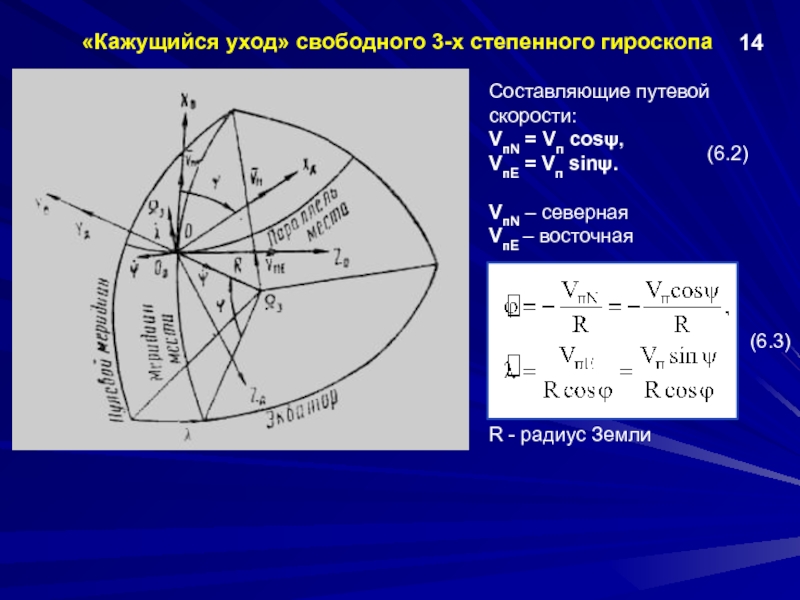
Уравнения «ухода» свободного 3-х степенного гироскопа с вертикально расположенным вектором кинетического момента

вектором кинетического момента
22
Принцип действия гироскопических авиагоризонтов основан на использовании свойства

трехстепенного гироскопа сохранять заданное направление кинетического момента неизменным в пространстве. Углы крена  и тангажа ϑ самолета измеряют с помощью трехстепенного гироскопа (рис. ), установленного на самолете.

Направление кинетического момента гироскопа совпадает с вертикалью места (ось ОZ), внешняя ось карданова подвеса совпадает с продольной осью самолета OX, а внутренняя — направлена по оси ОY, расположенной в горизонтальной плоскости.

вектором кинетического момента
21
При появлении угла тангажа внешняя ось подвеса поворачивается

вместе с самолетом, а гироузел не изменяет своего положения в пространстве. Вследствие этого угол поворота наружной рамы относительно внутренней оси карданова подвеса равен углу тангажа ϑ.
При накренении самолета вместе с ним поворачивается основание, на котором закреплен гироскоп. Наружная рама остается неподвижной. Угол поворота основания относительно наружной рамы равен углу крена  самолета .

вектором кинетического момента
20
Но положение истинной вертикали относительно инерциального пространства может

изменяться вследствие:
- суточного вращения Земли;
- движения ЛА относительно земной поверхности.
Допустим, при помощи трехстепенного гироскопа на ЛА, расположенном на экваторе воспроизводится направление истинной вертикали, которое стабилизируется относительно инерциального пространства. ЛА при этом неподвижен.

дополнительных мер, то даже при неподвижном ЛА с течением некоторого

времени наблюдатель заметит, что вектор Н гироскопа отклонился от заданного направления. На самом деле отклонилась поверхность Земли вследствие суточного вращения и теперь истинная вертикаль занимает новое положение в инерциальном пространстве, составляя некоторый угол  с моделируемой при помощи ГС вертикалью (рис., а). Очевидно, что через 6 часов гироскоп из вертикального станет горизонтальным. Это явление получило название "кажущегося ухода" гироскопа из-за вращения Земли.

гироскопа будет, если предположить, что ЛА совершает полет со скоростью

V относительно неподвижной Земли (рис., б). В этом случае, если не учитывать высоту полёта, истинная вертикаль повернется в инерциальном пространстве на угол

- угловая скорость движения ЛА относительно Земли.

Очевидно, что в реальных условиях два этих процесса происходят одновременно, вызывая отклонение приборной вертикали, т.е. того направления, которое указывает вектор Н гироскопа, от истинной вертикали.

случае вектор Н гироскопа будет уходить от требуемого направления

стабилизации с угловой скоростью , равной сумме угловых скоростей кажущегося ухода из-за вращения Земли  (переносное движение), из-за облёта Земли ЛА с угловой скоростью ω (относительное движение), а также из-за инструментальных дрейфов гироскопов :

(6.1)

вектором кинетического момента
16
Особенностью трехстепенного гироскопа является то, что направление

его кинетического момента сохраняется неизменным в мировом пространстве, а не относительно Земли. В связи с этим из-за собственного вращения Земли и перемещения самолета относительно Земли вертикаль места будет отклоняться от направления кинетического момента гироскопа.
Рассмотрим это явление, пренебрегая при этом высотой полета по сравнению с радиусом Земли.

положение самолета, определяемое широтой  и долготой . Заданная система

отсчета О0Х0Y0Z0 :
ось О0Х0 - на север, - ось О0Z0 - на восток,
ось О0Y0 по вертикали места. Самолет совершает полет с постоянной путевой скоростью Vп в горизонтальной плоскости (ϑ =  = 0) и с заданным углом курса .

В этом случае оси ОХдYдZд, связанные с траекторией, занимают в точке О0 следующее положение: ось ОYд совпадает с осью О0Y0, ось ОХд — направлена по вектору путевой скорости Vп, ось ОZд перпендикулярна осям ОХд и ОYд. Оси гироскопа ОХвYвZв в начальный момент полета совпадают с осями ОХдYдZд.

Xд

Z0

X0

Y0

Yд

Zд

VпN – северная
VпE – восточная
«Кажущийся уход» свободного 3-х степенного гироскопа

14

(6.2)

(6.3)

R - радиус Земли

эти оси
«Кажущийся уход» свободного 3-х степенного гироскопа
13
(6.4)
(6.5)
 - угловая

скорость вращения Земли

С учетом выражений (6.2), (6.3)

с самолетом и сохраняющего ось ОYд вертикальной, и неподвижного в

мировом пространстве трехгранника ОХвYвZв.

«Кажущийся уход» свободного 3-х степенного гироскопа

12

Угловые скорости определяют скорость «ухода» кинети-ческого момента гироскопа от вертикали места вследствие суточного вращения и движения самолета относительно Земли. За час полета углы отклонения кинетического момента от вертикали могут достигать нескольких градусов.
Кроме того, гироскоп отклоняется от заданного положения из-за наличия моментов трения в осях подвеса и моментов от небаланса.

невозмущаемый указатель вертикали места лишь в течение нескольких минут. Для

обеспечения более длительной работы трехстепенного гироскопа как указателя вертикали с необходимой точностью его следует снабдить корректирующим устройством.

«Кажущийся уход» свободного 3-х степенного гироскопа

11

В качестве чувствительных элементов корректирующих устройств в авиагоризонтах используют однокоординатные и двух координатные электролитические маятники.

двухкоординатный электролитический маятник 5, управляющий двумя коррекционными двигателями 1, 6.

На внешней и внутренней осях карданова подвеса располагаются устройства для съема результатов измерений 3, 4.

Хд

Yд

Yв

Zв

движения гироскопа воспользуемся методом суммирования моментов. Суммируя моменты, действующие по

внешней и внутренней осям карданова подвеса, получаем

Ми - моменты инерции; Мг - гироскопические моменты; Мт - моменты трения; Мк- корректирующие моменты.

Моменты инерции и моменты трения

Гироскопические моменты

проекции абсолютной угловой скорости движения гироскопа в мировом пространстве

(6.8)

(6.7)

(6.6)

на оси ОХв и ОZв
Полагая углы г и г малыми,

из (6.8), с учетом (6.9) получаем

Выражения для корректирующих моментов

с1, с2 - коэффициенты пропорциональности системы коррекции;
м, м - углы отклонения осей корректирующих маятников по отношению к осям гироузла

(6.9)

(6.10)

(6.11)

осей корректирующих маятников
мв, мв — отклонения маятников, обусловленные действием

внешних возмущений (ускорения при маневрировании и вибрации).

Знаки корректирующих моментов в выражениях (6.10) выбраны таким образом, чтобы при отклонении гироскопа от вертикали он возвращался бы к ней под влиянием корректирующих моментов.

Уравнения движения авиагоризонта (6.6) с учетом выражений (6.7), (6.10-6.12) запишутся в виде

(6.12)

(6.13)

м = -г+мв, м= -г+мв,

Методические погрешности складываются из скоростных и баллистических девиаций авиагоризонта.

скоростных девиаций рассмотрим уравнения (6.13) для случая прямолинейного движения самолета

с постоянной скоростью ( = мв = мв = =0) и без учета инерционности рам карданова подвеса и трения в осях подвеса.

Частные решения уравнений (6.14)

(6.14)

k1 = c1/H, k2 = c2/H.

уравнений (6.14) являются скоростными девиациями авиагоризонта. У современных авиагоризонтов значения

скоростных девиаций составляют несколько угловых секунд.

Из изложенного следует, что при введении пропорциональной кор-рекции трехстепенной гироскоп не «уходит» от вертикали места под действием угловых скоростей
, а устанавливается в положение, практически не отличающееся от вертикального.
 

прямолинейного движения самолета
=

0 с постоянным ускорением .

Пренебрегая малыми угловыми скоростями ,
и без учета инерционности рам карданова подвеса и трения в осях подвеса систему уравнений (6.13)  

«Кажущийся уход» свободного 3-х степенного гироскопа, возникающий в прямолинейном полете с ускорением

4

(6.15)

k1 = c1/H, k2 = c2/H.

(6.13)

запишем в виде

полете с ускорением
3
Решением второго уравнения (6.15) является равенство

. Первое уравнение при нулевых начальных условиях имеет следующее решение:

(6.16)

Таким образом, как следует из уравнения (6.16), ось гироскопа авиагоризонта при действии продольного ускорения апериодически приближается к положению кажущейся вертикали, при этом

полете с ускорением

Пренебрегая инерционностью рам карданова подвеса, вязким трением в подвесе, малыми

угловыми скоростями

и полагая =0; мв = мв = 0, и без учета инерционности рам карданова подвеса уравнения (6.13) запишем в виде:

Основные причины возникновения дрейфа гироскопа:
- разбалансировка (дебаланс), т.е. несовпадение центра подвеса гироузла с центром масс гироскопа;
- моменты сил сухого и жидкостного (вязкого) трения;
- моменты токоподводов;
- моменты датчиков углов;
- моменты сил инерции рам карданова подвеса и др.

«Кажущийся уход» свободного 3-х степенного гироскопа, обусловленный «дрейфом»

2

(6.17)

«дрейфом»
1
(6.17)
н = г(0), н = г(0).
Из решений (6.17) следует, что

при отклонении авиагоризонта на углы н и н ось его гироскопа не может возвратиться в вертикальное положение, а будет составлять с вертикалью места углы , определяющие зону застоя от трения.