Слайд 1Лекция № 7
Тема: Математические модели теории надежности
Вопросы:
1. Общие понятия о
моделях надежности
2. Статистическая обработка результатов испытаний и определение ПН
3. Расчёт
критерия согласия
4. Законы распределения наработки до отказа
КиДвТП
Слайд 21 Общие понятия о моделях надежности
Для решения задач по
оценке надежности и прогнозированию работоспособности объекта необходимо иметь мат. модель,
которая представлена аналитическими выражениями одного из показателей P(t), a(t) или λ(t).
Рассмотрим U – образную кривую для интенсивности отказов λ(t) большинства невосстанавливаемых объектов. Каждый из трех участков (приработки, нормальной эксплуатации и старения) имеет характерную зависимость λ(t) и, следовательно, свою математическую модель.
Основной путь для получения модели состоит в проведении испытаний, вычислении статистических оценок и их аппроксимации аналитическими функциями. Вид аналитической функции, описывающей изменение показателей надежности P(t), a(t) или λ(t), определяет закон распределения СВ, который выбирается в зависимости от свойств объекта, его условий работы и характера отказов.
Слайд 32 Статистическая обработка результатов испытаний и определение ПН
Пусть в
результате испытаний N0 невосстанавливаемых одинаковых объектов получена статистическая выборка –
массив наработки до отказа каждого из N0 испытанных объектов. Такая выборка характеризует СВ наработки до отказа объекта.
Необходимо выбрать закон распределения СВ T и проверить правильность выбора по соответствующему критерию.
Подбор закона распределения осуществляется на основе аппроксимации экспериментальных данных о наработке до отказа, которые должны быть представлены в наиболее компактном графическом виде. Выбор той или иной аппроксимирующей функции носит характер гипотезы, которую выдвигает исследователь. Экспериментальные данные могут с большей или меньшей вероятностью подтверждать или не подтверждать справедливость той или иной гипотезы. Поэтому исследователь должен получить ответ на вопрос: согласуются ли результаты эксперимента с гипотезой о том, что СВ наработки подчинена выбранному им закону распределения?
Слайд 42 Статистическая обработка результатов испытаний и определение ПН
Алгоритм обработки
результатов и расчета ПН
1. Формирование статистического ряда
При большом числе испытываемых
объектов полученный массив наработок {t1, ti,…,...,tn} является громоздкой и мало наглядной формой записи случайной величины T. Поэтому для компактности и наглядности выборка представляется в графическом изображении статистического ряда – гистограмме наработки до отказа. Для этого необходимо:
Слайд 6
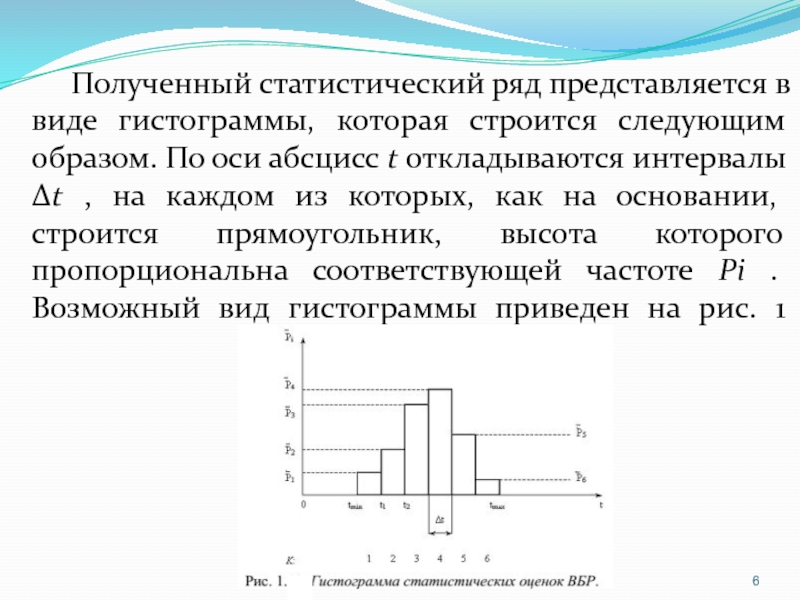
Полученный статистический ряд представляется в виде гистограммы, которая строится следующим
образом. По оси абсцисс t откладываются интервалы ∆t , на
каждом из которых, как на основании, строится прямоугольник, высота которого пропорциональна соответствующей частоте Pi . Возможный вид гистограммы приведен на рис. 1
Слайд 7
2. Расчет эмпирических функций. Используя данные сформированного статистического ряда, определяются
статистические оценки показателей надежности, т. е. эмпирические функции:
- функция распределения
отказов (оценка ВО)
Слайд 8
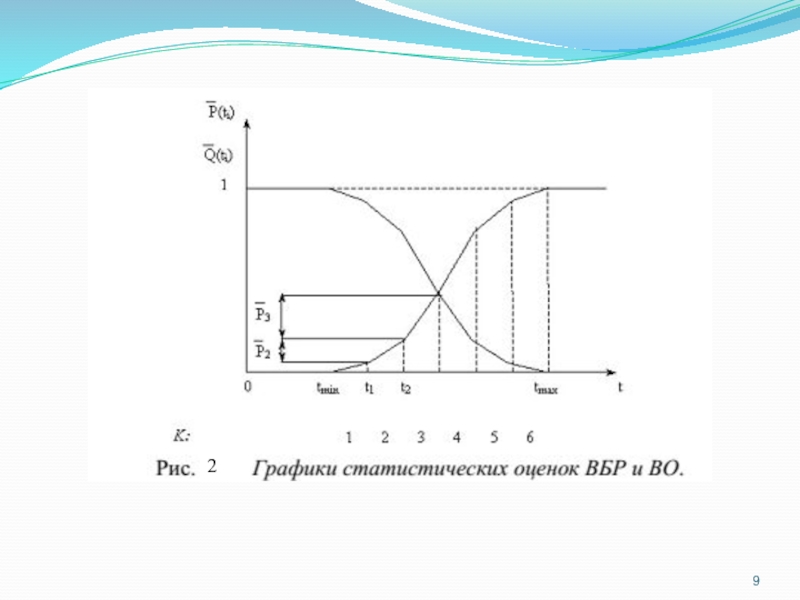
функция надежности (оценка ВБР)
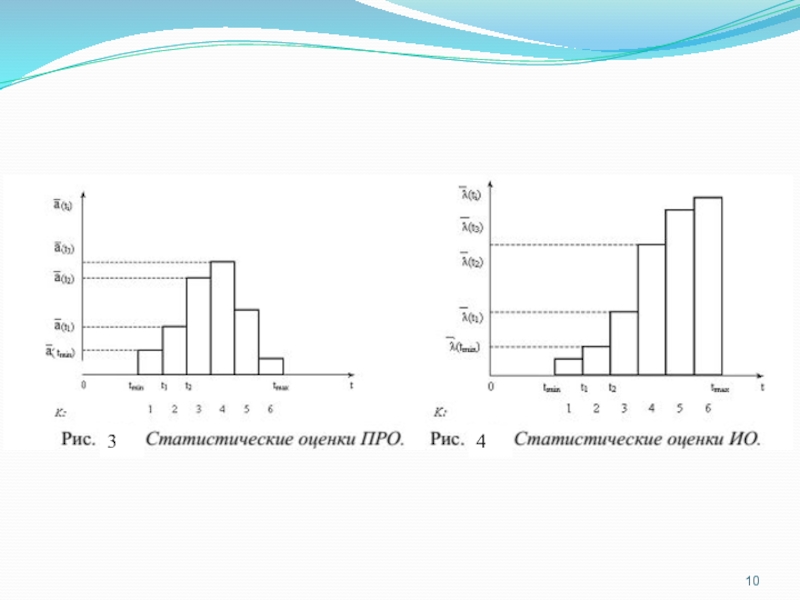
На рис. 2-4 приведены соответственно графики статистических
оценок Q (t), a(t),λ (t).
Слайд 12
3. Расчет статистических оценок числовых характеристик
Для расчета статистических оценок числовых
характеристик можно воспользоваться данными сформированного статистического ряда. Определяются такие оценки:
- оценка средней наработки до отказа (статистическое среднее наработки):
- оценка дисперсии наработки до отказа (эмпирическая дисперсия наработки):
Слайд 15
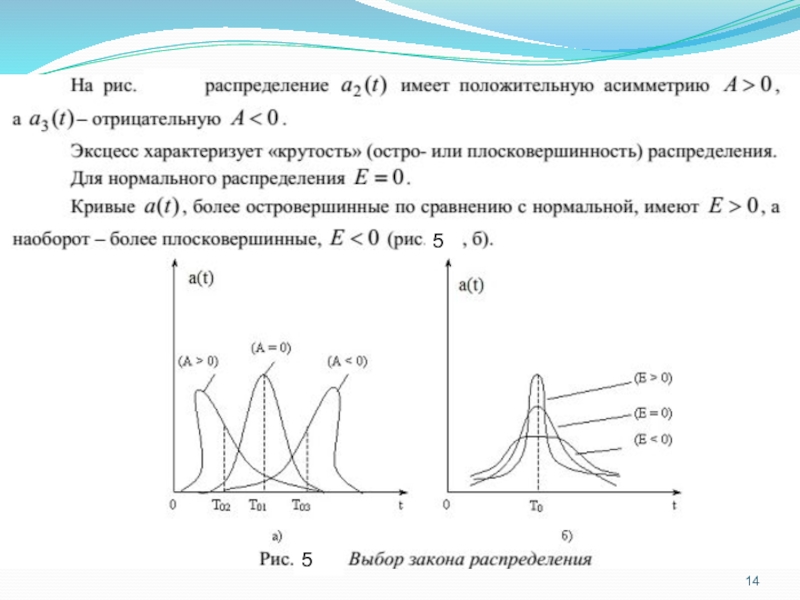
Выбор закона распределения состоит в подборе аналитической функции, наилучшим образом
аппроксимирующей эмпирические функции надежности. Выбор - процедура неопределенная и во
многом субъективная, при этом многое зависит от априорных знаний об объекте и его свойствах, условиях работы, а также анализа вида графиков P(t), a(t) или λ (t).
Очевидно, что выбор распределения будет зависеть, прежде всего, от вида эмпирической функции ПРО a(t) , а также от вида - λ (t) . Т.е., выбор закона распределения носит характер принятия той или иной гипотезы.
Слайд 16
3 Расчет критерия согласия
Критерий согласия – это критерий проверки гипотезы
о том, что случайная величина T, представленная своей выборкой, имеет
распределение предполагаемого типа.
Проверка состоит в следующем. Рассчитывается критерий, как некоторая мера расхождения теоретического и эмпирического распределений, причем эта мера является случайной величиной. Чем больше мера расхождения, тем хуже согласованность эмпирического распределения с теоретическим, и гипотезу о выборе закона распределения следует отвергнуть, как мало правдоподобную. В противном случае – экспериментальные данные не противоречат принятому распределению. Из известных критериев наиболее применяемый критерий согласия χ2 (хи-квадрат) Пирсона.
Слайд 194 Законы распределения наработки до отказа
Вид аналитической функции, описывающей изменение
показателей надежности
P(t) , a(t) или λ(t) , определяет закон распределения
случайной величины, который выбирается в зависимости от свойств объекта, его условий работы и характера отказов. Наиболее распространенными являются следующие законы распределения:
1. Экспоненциальное распределение;
2. Распределение Релея;
3. Распределение Вейбулла;
4. Классическое нормальное распределение (нормальный закон распределения наработки до отказа);
5. Логарифмически нормальное распределение;
6. Гамма-распределение.