Лекция №11 Солодухин Е.А

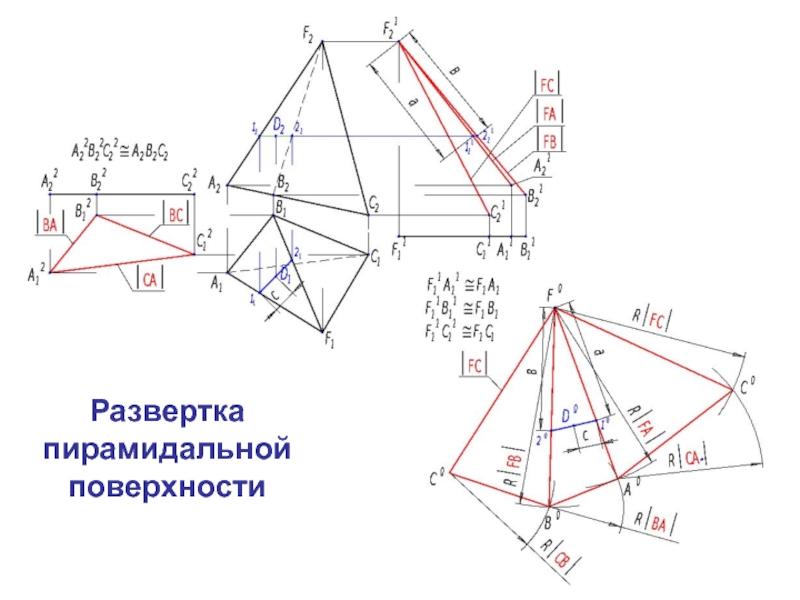
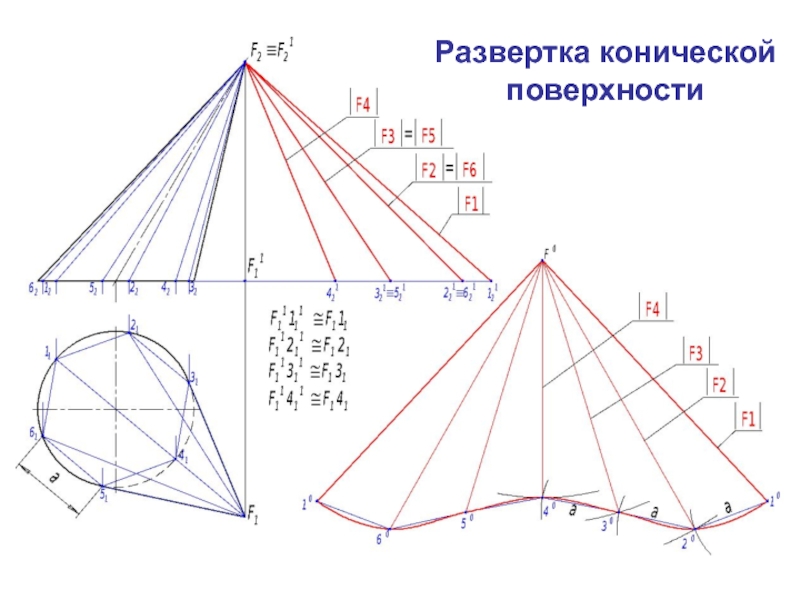
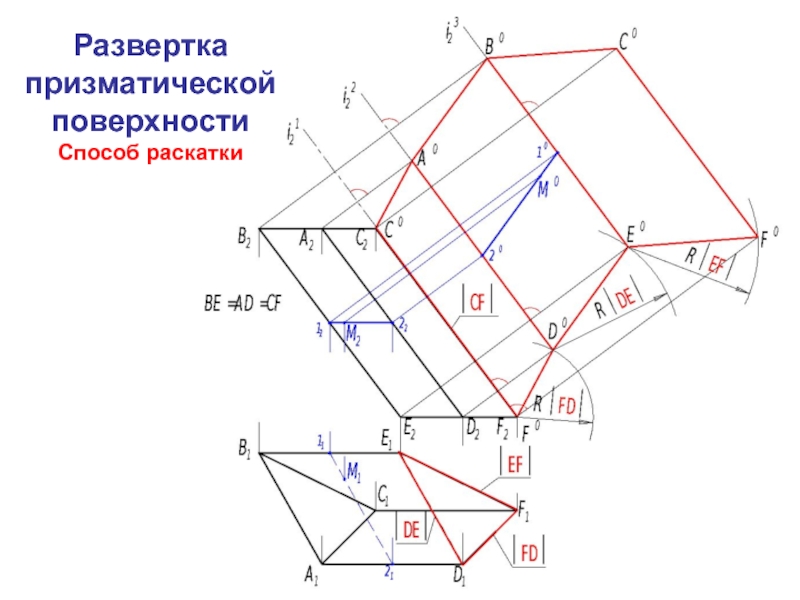
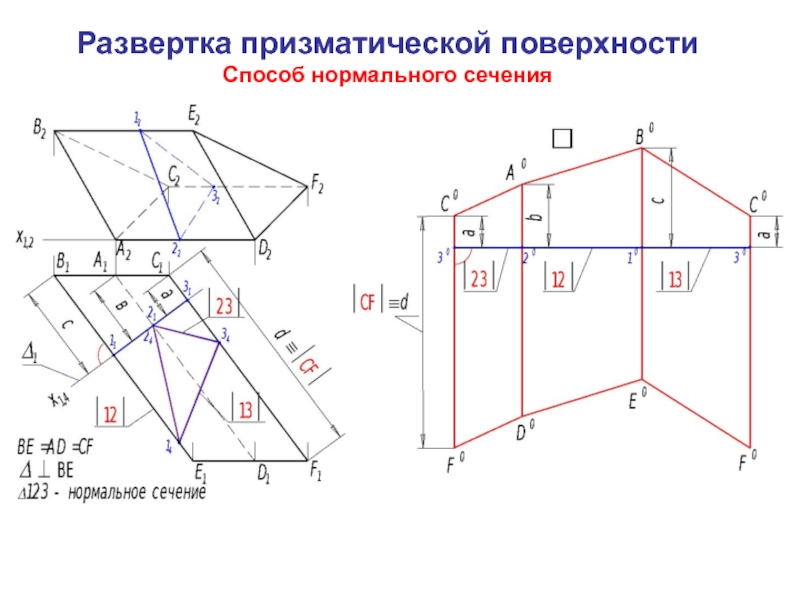
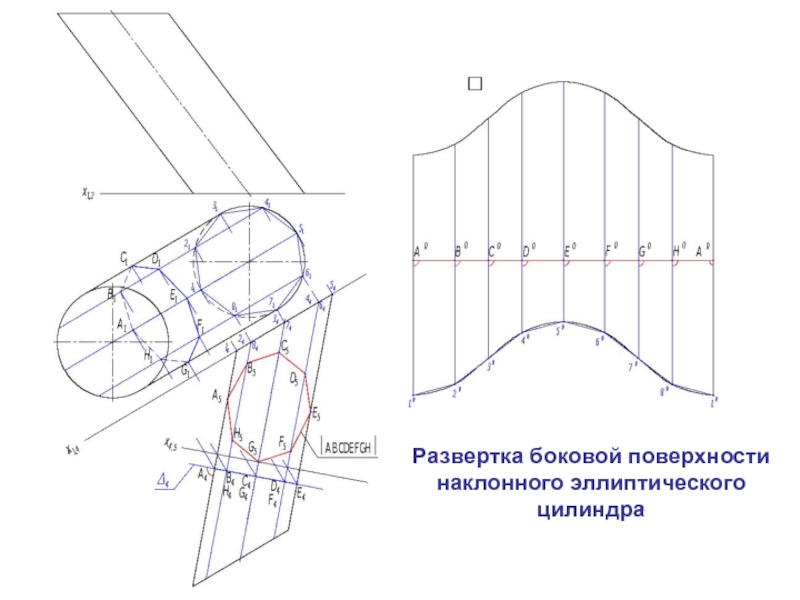
которой совмеще-ны с одной плоскостью.
Поверхности бывают развертывающимися и неразвертывающимися.
Поверхность

считается развертывающейся, если она совмещается с одной плоскостью всеми своими точками без разрывов и складок.
К таким поверхностям относятся гранные и торсовые поверхности.
Поверхность считается неразвертывающейся, если она не может быть совмещена с одной плоскостью всеми своими точками без разрывов и складок.
Практически это все остальные поверхности.

фигуры может быть точно определена с помощью математических формул.
В

противном случае развертка приближен-ная.
При построении приближенных разверток заданная поверхность заменяется (аппрокси-мируется) другими развертывающимися поверхностями – гранными, цилиндрическими или коническими.

истинную величину.

пирамидальной и конической поверхности;
раскатки и нормального сечения – для призматической

и цилиндрической поверхности.
Для построения разверток неразвертыва-ющихся поверхностей используют способы:
вспомогательных треугольников;
вспомогательных конусов;
вспомогательных цилиндров.

поверхности с одной плоскостью.
Так как все грани многогранника являют-ся отсеками

плоскостей в виде плоских мно-гоугольников, в основе построения развер-тки лежит определение истинной величины этих многоугольников.
Для определения точной формы и разме-ров любого многоугольника его делят на смежные треугольники (триангуляция).

в слу-чае построения развертки боковой поверх-ности пирамиды – способом треугольников.

Для этого коническая поверхность заме-няется (аппроксимируется) вписанной в нее многогранной пирамидальной поверхнос-тью.
Чем больше число граней у вписанной пирамиды, тем меньше будет разница между действительной и приближенной разверткой конической поверхности.

ребра призматической или образующие цилиндрической поверхности являлись прямыми частного положения

- прямыми уровня.
Если перечисленные геометрические элементы находятся в общем положении, то необходимо на основе способа перемены плоскостей проекций преобразовать исходные проекции до нужного положения этих элементов.

в случае построения развертки боковой поверхности призмы – способом раскатки

или нормального сечения.
Для этого цилиндрическая поверхность заменяется (аппроксимируется) вписанной в нее многогранной призматической поверх-ностью.
Чем больше число граней у вписанной призмы, тем меньше будет разница между действительной и приближенной разверткой цилиндрической поверхности.