Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №5
Содержание
- 1. Лекция №5
- 2. Основные понятияУгол, образованный гранями, сходящимися в одной
- 3. Основные понятияПРИЗМА - многогранник, две грани которого
- 4. Основные понятияПирамида – многогранник, основание которого –
- 5. Основные понятияТела Платона-это выпуклые многогранники, все грани
- 6. Точка и многогранникТочка принадлежит поверхности многогранника если
- 7. Сечение многогранников плоскостьюСечение многогранника представляет собой некоторый
- 8. Сечение многогранника плоскостью1 способАлгоритм решенияЗаключаем боковые грани
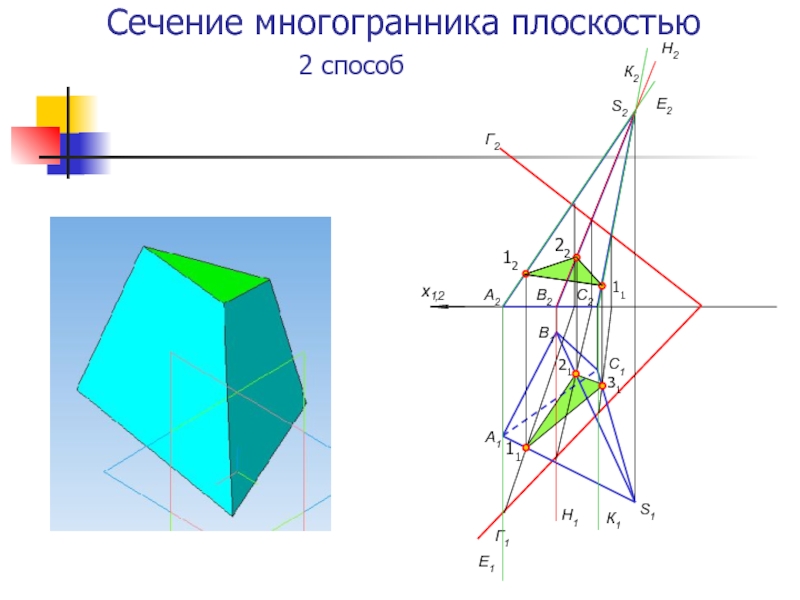
- 9. Сечение многогранника плоскостью2 способ
- 10. Пересечение многогранника прямой Определяем точки пересечения прямой
- 11. Взаимное пересечение многогранников 1 способ:Строят точки пересечения ребер
- 12. Взаимное пересечение многогранников1 способ
- 13. Развёрткой поверхности многогранника называется плоская фигура, полученная
- 14. Развертка призматической поверхностиПо способу треугольников:четырехугольники (грани) разбивают
- 15. Развертка призматической поверхности
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция №5
Многогранники
Основные понятия;
Точка и многогранник
Сечение многогранника плоскостью
Пересечение многогранника с прямой
линией
Слайд 2Основные понятия
Угол, образованный гранями, сходящимися в одной точке – вершине,
называется многогранным углом.
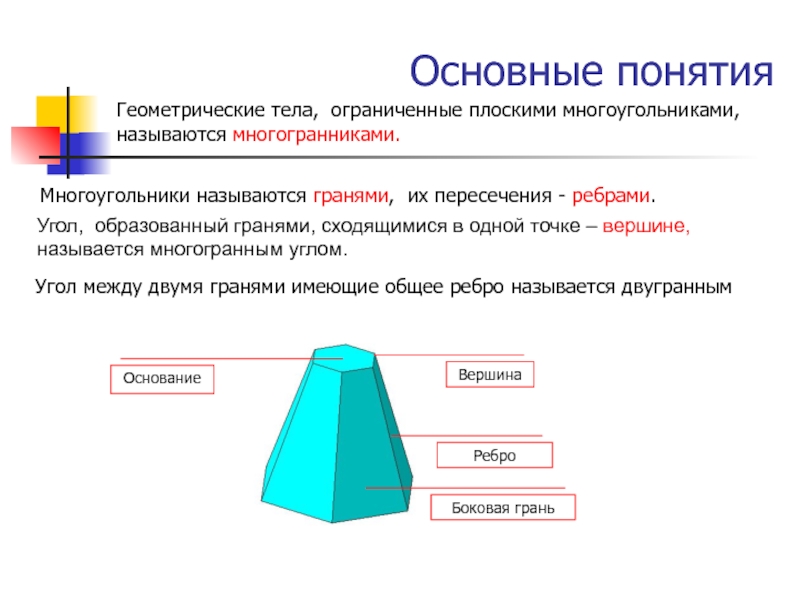
Геометрические тела, ограниченные плоскими многоугольниками, называются многогранниками.
Многоугольники называются
гранями, их пересечения - ребрами.Вершина
Ребро
Боковая грань
Угол между двумя гранями имеющие общее ребро называется двугранным
Основание
Слайд 3Основные понятия
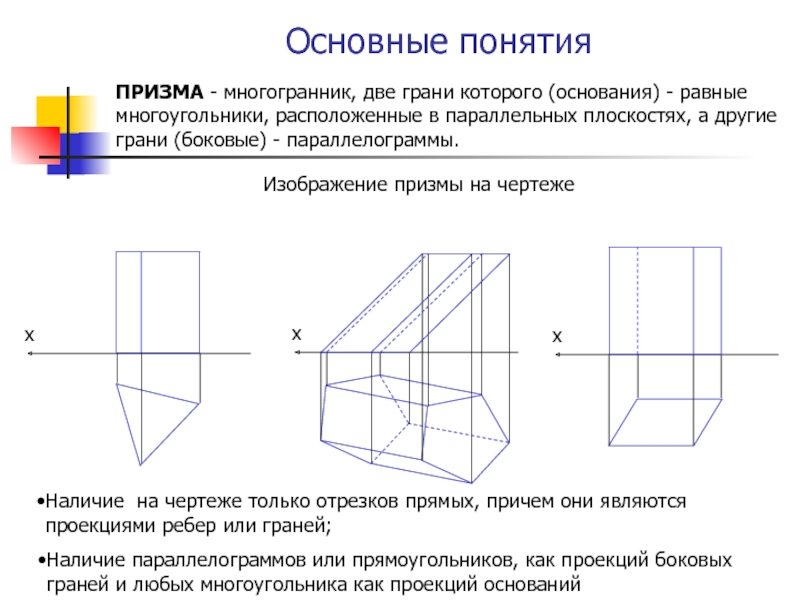
ПРИЗМА - многогранник, две грани которого (основания) - равные
многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) -
параллелограммы.Изображение призмы на чертеже
Наличие на чертеже только отрезков прямых, причем они являются проекциями ребер или граней;
Наличие параллелограммов или прямоугольников, как проекций боковых граней и любых многоугольника как проекций оснований
Слайд 4Основные понятия
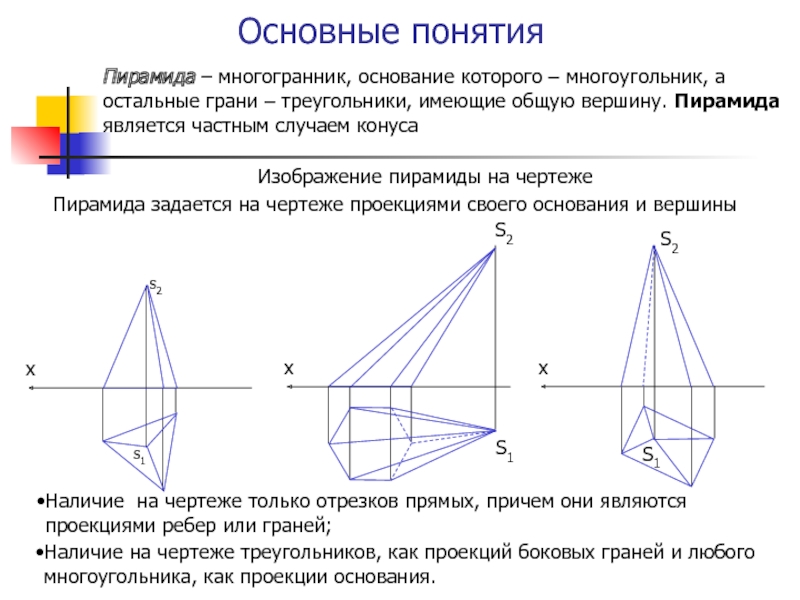
Пирамида – многогранник, основание которого – многоугольник, а остальные
грани – треугольники, имеющие общую вершину. Пирамида является частным случаем
конусаИзображение пирамиды на чертеже
Пирамида задается на чертеже проекциями своего основания и вершины
Наличие на чертеже треугольников, как проекций боковых граней и любого многоугольника, как проекции основания.
Наличие на чертеже только отрезков прямых, причем они являются проекциями ребер или граней;
Слайд 5Основные понятия
Тела Платона-это выпуклые многогранники, все грани которых правильные многоугольники.
Выпуклых правильных многогранников всего пять: тетраэдр, куб, октаэдр, додекаэдр и
икосаэдр.Все многогранные углы правильного многогранника конгруэнтны.
Тетраэдр-четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками (огонь).
Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами (земля)
Октаэдр-восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками (вода)
Додекаэдр-двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник (воздух)
Икосаэдр-двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками (quinta essentia «пятая сущность»).
Слайд 6Точка и многогранник
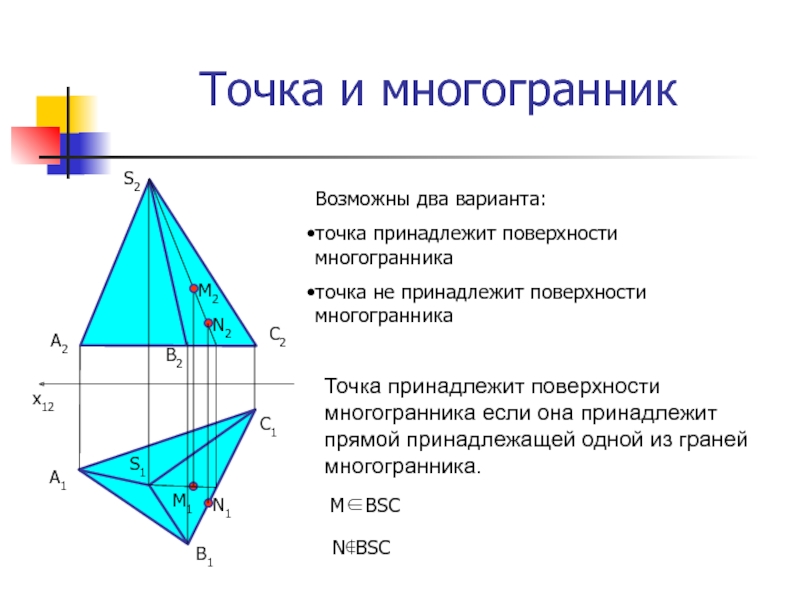
Точка принадлежит поверхности многогранника если она принадлежит прямой
принадлежащей одной из граней многогранника.
Возможны два варианта:
точка принадлежит поверхности
многогранника точка не принадлежит поверхности многогранника
MBSC
NBSC
Слайд 7Сечение многогранников плоскостью
Сечение многогранника представляет собой некоторый многоугольник, вершины которого
расположены на ребрах многогранника.
Первый способ заключается в построении линий пересечения
граней многогранника с секущей плоскостью и в непосредственном получении сторон сечения.Второй способ заключается в построении точек пересечения рёбер многогранника с секущей плоскостью и в последовательном соединении полученных таким образом вершин, прямыми линиями.
Способы построения фигур сечения:
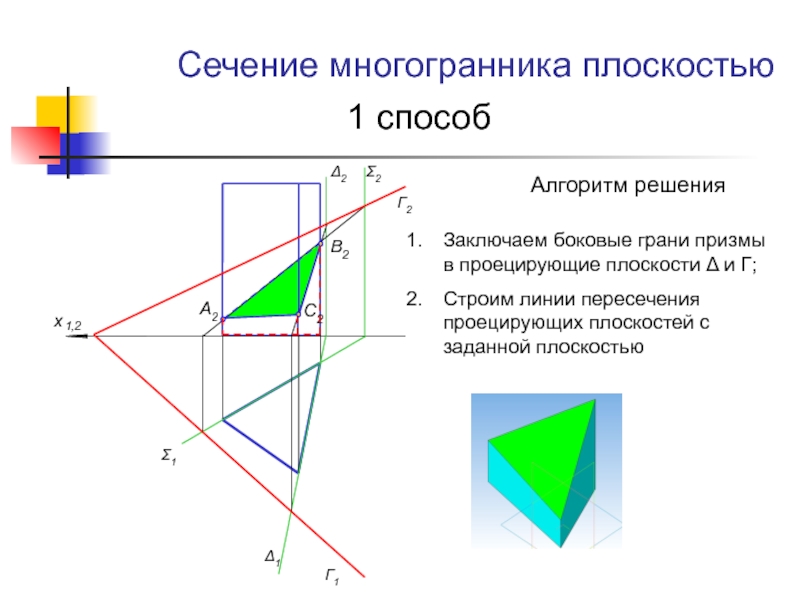
Слайд 8Сечение многогранника плоскостью
1 способ
Алгоритм решения
Заключаем боковые грани призмы в проецирующие
плоскости и Г;
Строим линии пересечения проецирующих плоскостей с заданной
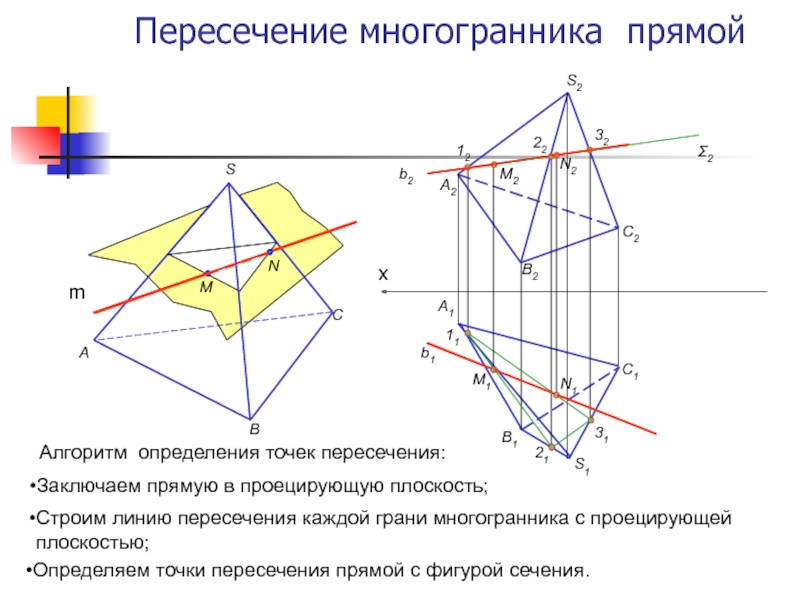
плоскостьюСлайд 10Пересечение многогранника прямой
Определяем точки пересечения прямой с фигурой сечения.
Алгоритм
определения точек пересечения:
Заключаем прямую в проецирующую плоскость;
Строим линию пересечения каждой
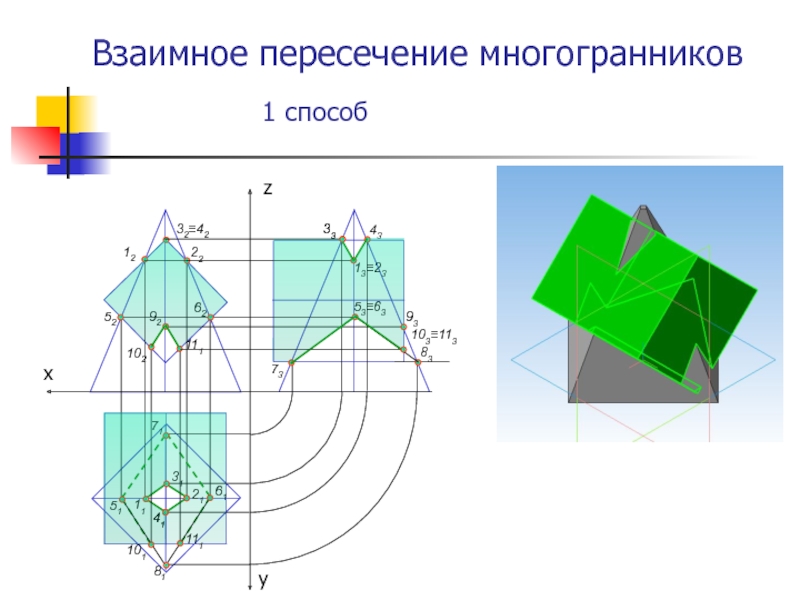
грани многогранника с проецирующей плоскостью;Слайд 11Взаимное пересечение многогранников
1 способ:
Строят точки пересечения ребер одного многогранника с
гранями другого и ребер второго с гранями первого. Через построенные
точи в определенной последовательности проводят ломаную линию пересечения данных многогранников (задача на пересечение прямой линии с плоскостью). При этом отрезки прямых проводят лишь через те построенные точки, которые лежат на одной и той же грани.2 способ:
Строят отрезки прямых, по которым грани одной поверхности пересекают грани другой (задача на пересечение двух плоскостей).
Способы построения линии пересечения:
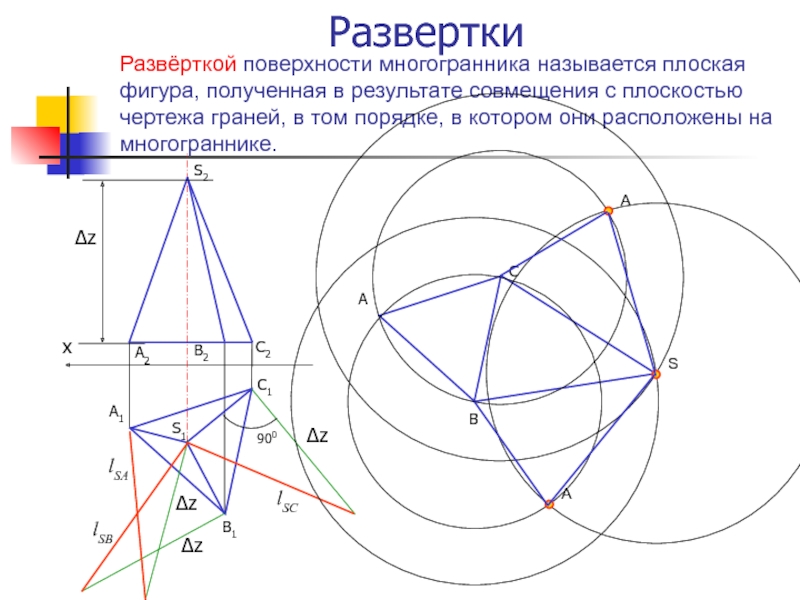
Слайд 13Развёрткой поверхности многогранника называется плоская фигура, полученная в результате совмещения
с плоскостью чертежа граней, в том порядке, в котором они
расположены на многограннике.Развертки
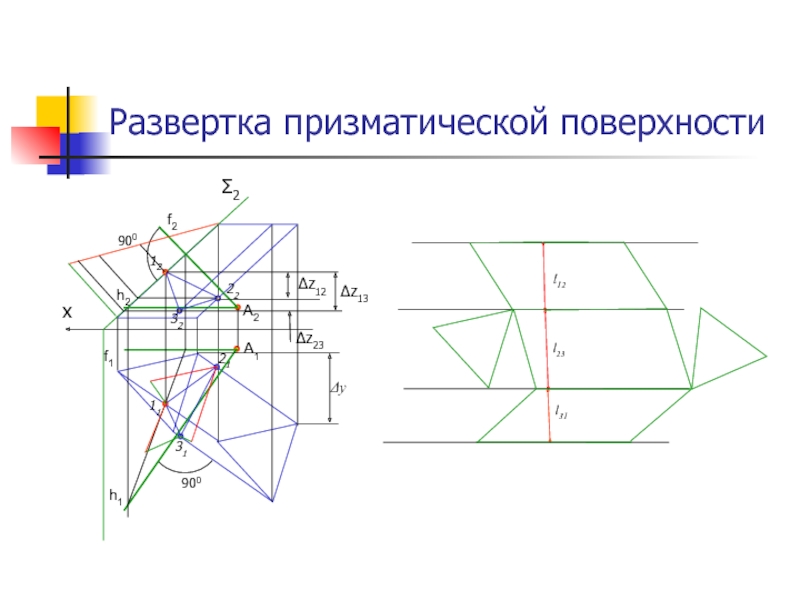
Слайд 14Развертка призматической поверхности
По способу треугольников:
четырехугольники (грани) разбивают диагоналями на треугольники;
определяют
длины сторон треугольников;
выполняют чертеж развертки последовательным построением треугольников, на которые
разбиты грани.Развертку призматической поверхности можно производить способами: нормального сечения и треугольников.
При способе нормального сечения:
пересечь призматическую поверхность вспомогательной плоскостью, перпендикулярной к ребрам;
развернуть построенную ломаную линию пересечения вспомогательной плоскости с призматической поверхностью, определив длину ее отрезков;
на перпендикулярах к развернутой линии пересечения отложить длину отрезков ребер призматической поверхности и соединить их концы отрезками прямых.